基于改进AHP法的桥梁加固方案灰关联度优选分析
2018-01-08杨永清
杨 灯, 杨永清
(西南交通大学土木工程学院,四川成都 610031)
基于改进AHP法的桥梁加固方案灰关联度优选分析
杨 灯, 杨永清
(西南交通大学土木工程学院,四川成都 610031)
为了更为合理地选择出桥梁最优加固方案,文章建立了基于改进AHP法的桥梁加固方案灰关联度优选模型。首先,引入10/10~18/2标度法构造两两对比判断矩阵,解决了传统层次分析法(AHP)中1~9标度法等级关系不合理的问题。然后通过最优传递矩阵改进传统AHP法,避免了传统AHP法中判断矩阵的一致性检验问题,并结合灰色关联度法建立出了用于桥梁加固方案优选的评价模型。最后,对工程实例的分析和计算结果表明,该决策方法具有较好的可行性与合理性。
桥梁加固; 加固方案优选; 改进AHP法; 灰色关联度
对既有桥梁进行加固改造,是提高其结构承载力、刚度及耐久性、延长使用寿命、提升使用功能的有效途径[1]。桥梁加固方案的选择对加固改造工程的质量与社会经济效益有重大影响,是项目成功与否的关键所在[2]。张鹏[3]构建了桥梁加固方案的评价指标体系,并基于AHP法实现了桥梁加固方案的优选;杨雅勋等[4]做了进一步工作,通过结合AHP法和熵值法对评价指标进行赋权,建立了基于组合权值的灰关联法来对桥梁加固方案进行优选;边晶梅等[5]同样采用组合权值的方法建立了桥梁加固方案进行优选的简化ELECTRE法模型;文献[3-5]中采用的层次分析法均是利用传统的1~9标度法构造判断矩阵;徐泽水[6]通过对四种标度法的分析,指出10/10~18/2标度法的性能最好,而1~9标度法的等级关系欠缺合理性,难以反映人们的判断。因此,本文在上述研究的基础上提出采用改进的AHP法确定指标权重,建立灰色关联度优选模型进行桥梁加固方案的优选研究,使优选过程更具合理性与可靠性。
1 桥梁加固方案优选模型
1.1 建立评价指标体系
结合文献[3-5],通过分析旧桥加固的特点和技术要求,确定了影响加固方案评价的指标主要包括加固方案的效果可靠性、经济合理性、技术可行性以及加固后结构美观性四个方面。基于此,建立如表1所示的用于桥梁加固方案优选的二级评价指标体系。体系中包含4个一级评价指标Ei(i=1,2,3,4)和各一级指标对应的若干二级评价指eij(i=1,2,3,4;j的取值等于各一级指标对应的二级指标的个数)。
从表1中可以看出桥梁加固方案优选过程中所涉及到的评价指标较多。因此,实际优选过程中通常借助模糊理论进行简化处理,将各评价因素按其性质分为若干等级,在定性目标的论域[0,1]上给出评定值。桥梁加固方案优选中一般采用七级因素集,即U={很差,差,较差,中,较好,好,很好}={0.05,0.20,0.35,0.50,0.65,0.80,0.95},从而获得桥梁加固方案优选的决策矩阵R。
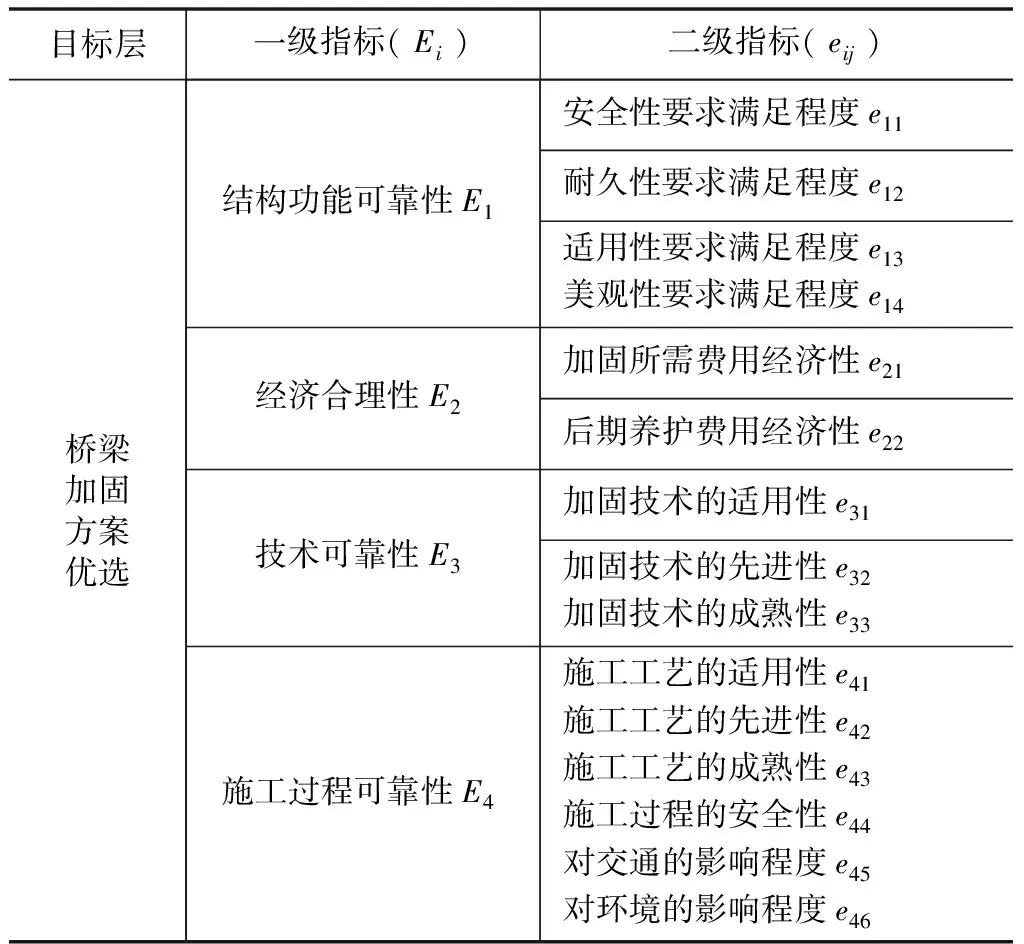
表1 桥梁加固方案评价指标体系
1.2 改进AHP法的基本原理
改进的AHP法和传统的AHP法都需要首先建立如表1所示的层次结构模型,即评价指标体系;然后通过专家对待评价的因素进行两两比较,从而判断其相对重要性,构造判断矩阵。但在传统AHP法中,如果构造的判断矩阵不满足一致性检验,则需要对判断矩阵进行调整,使其满足一致性。对判断矩阵的调整往往带有主观性和盲目性,有时可能导致评价结果的失真,选出实际上并不合理的桥梁加固方案。为了解决传统层次分析法的不足之处,采用最优传递矩阵的概念,建立改进的AHP法模型,使构造的判断矩阵自然满足一致性要求,并直接求出指标的权重。图1为传统AHP法与改进AHP法的计算流程对比图,从图中可以看出改进的AHP法较传统AHP法具有明显的优势。
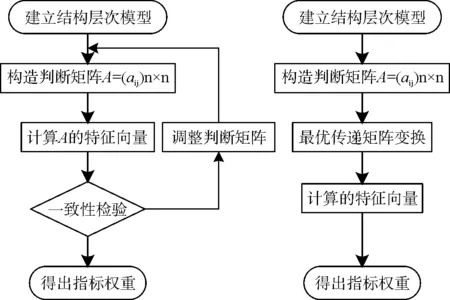
(a)传统的AHP法 (b)改进的AHP法图1 两种AHP法的计算流程
为使评价结果更具可信度,采用10/10~18/2标度法代替传统层次分析法中的1~9标度法来构造判断矩阵A=(aij)n×n,其中aij表示指标i与指标j的相对重要程度比值,aij为10/10时表示指标i与指标j同样重要。10/10~18/2标度法的具体转换关系与对应关系如表2所示。
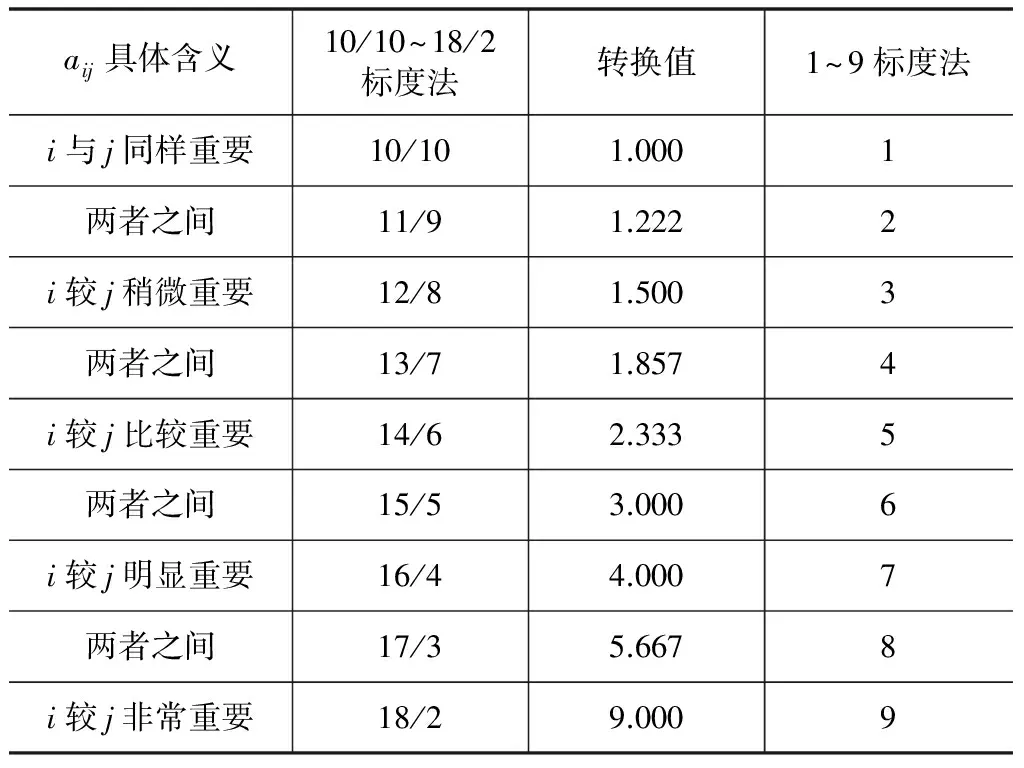
表2 10/10~18/2标度法
1.3 基于改进AHP法的指标权重
采用改进的AHP法求解判断矩阵权重,即指标权重的具体步骤如下[7]:
(1)计算判断矩阵A的对数传递矩阵B=(bij)n×n
bij=lg(aij),i,j=1,2,…,n
(1)
(2)计算对数传递矩阵B的最优传递矩阵C=(cij)n×n,cij的计算式为
(2)

(3)
(4)采用方根法求解拟优传递阵A*的特征向量Z=(z1,z2,…,zn),并对其进行归一化即可得出评价指标的最终权重向量W=(w1,w2,…,wn)。
1.4 基于灰色关联度法的加固方案优选模型
灰色关联度法是一种基于关联度大小来分析问题的综合评价方法,可用与桥梁加固方案的优选分析。假设有m个桥梁加固方案和n个评价指标,并设参考数列为x0={x0(k)|k=1,2,…,n},比较数列为xi={xi(k)|k=1,2,…,n},i=1,2,…,m。则比较序列xi对参考序列x0在第k个指标上的灰色关联系数表示如下[8]:
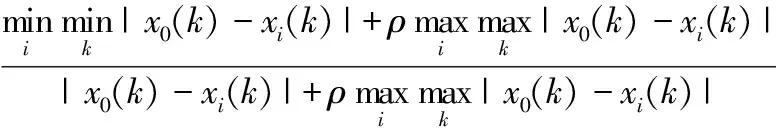
(4)
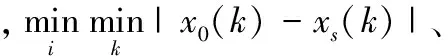
在求得各灰关联度系数后,结合前述改进的AHP法确定的各指标权重W=(w1,w2,…,wn), 可以计算出各方案加权关联度,由此建立出基于改进AHP法的桥梁加固方案灰关联度优选模型如下:
(5)
式中:ri为第i个加固方案对理想方案的灰色加权关联度。根据灰色加权关联度的大小,可对各加固方案进行排序,关联度越大,则其评价结果越好,即该方案为优选方案。
2 应用分析
以文献[3]中的工程实例作为本文的研究对象。某高速公路上跨有主桥为3×20 m现浇钢筋混凝土连续箱梁的立交桥。调查发现,该立交桥在建成通车16个月后,其两边孔距离桥台大约9 m处的中孔跨中附近梁底和腹板出现了少量的集中裂缝,最大宽度达0.2 mm,且桥梁具有较大挠度。经过复核设计、现场检查和荷载试验后,认为上述现象是由施工不合理卸架和早期施工车辆等荷载作用所引起,并在通车后进一步劣化所造成的。根据该桥梁的实际情况,初步提出了Ⅰ体外预应力加固、Ⅱ粘贴钢板加固、Ⅲ增焊主筋或喷射混凝土、Ⅳ粘贴碳纤维加固共四个加固方案进行选择。
(1)根据专家对每个方案的各指标给出的评定值,建立出如表3所示的加固方案评价矩阵R。
(2)采用10/10~18/2标度法构造评价指标的两两对比判断矩阵,第一层评价指标的判断矩阵如表4所示。限于篇幅,其它判断矩阵不详细列举。
(3)通过式(1)~式(3)可计算出各指标的权重值,取评价指标在各方案中的最大评定值构成理想方案,采用式(4)~式(5)计算出各方案与理想方案的关联度,详细结果汇总如表5所示。
从表5中的结果可以看出,体外预应力法为该桥梁的最优加固方法,优选结果与实际所采用的加固方法一致。对于具体的加固项目我们应该具体分析,充分结合其受损特征、外部环境等对各加固方案进行评价,确保选出最适合的桥梁加固方案。
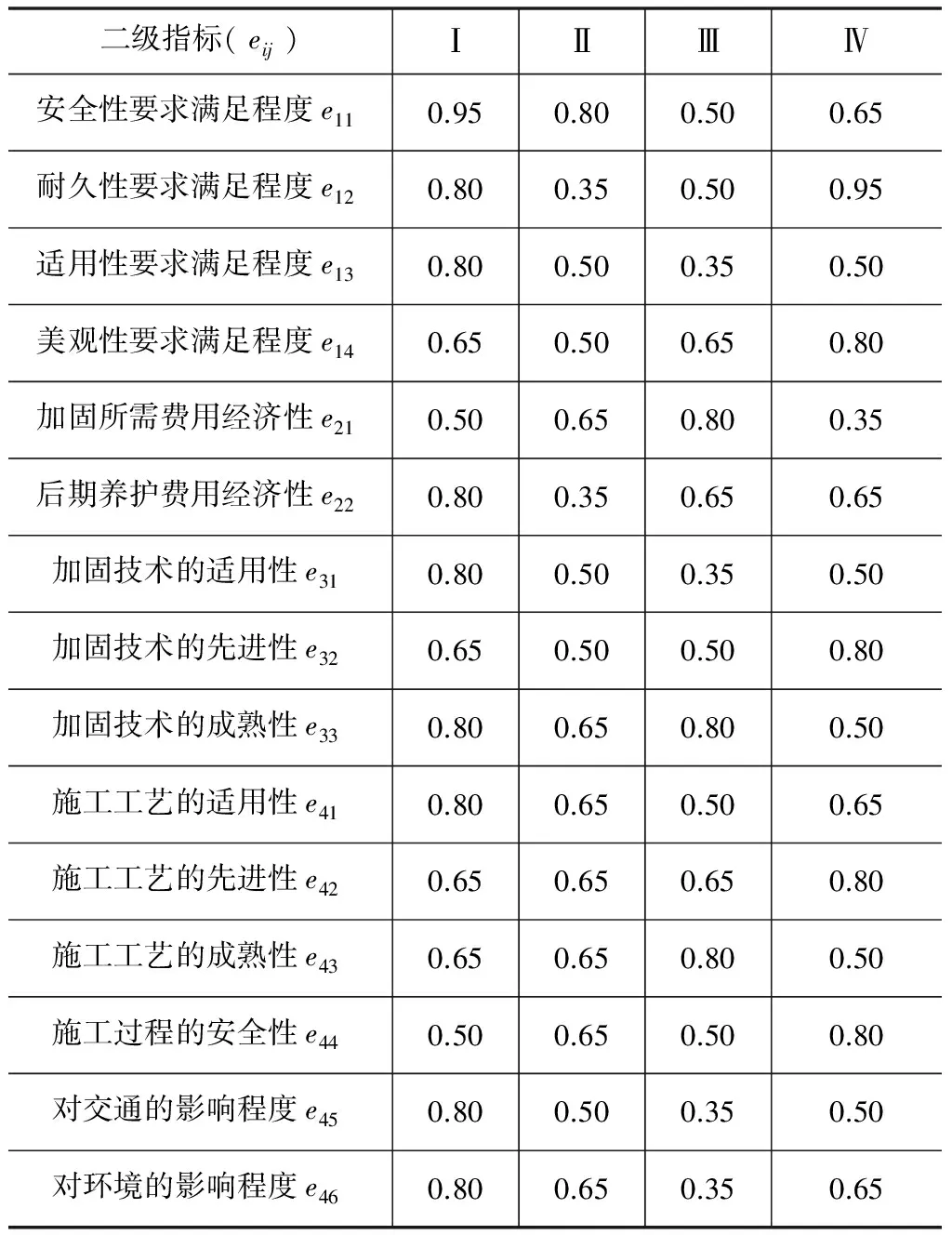
表3 桥梁加固方案评价矩阵
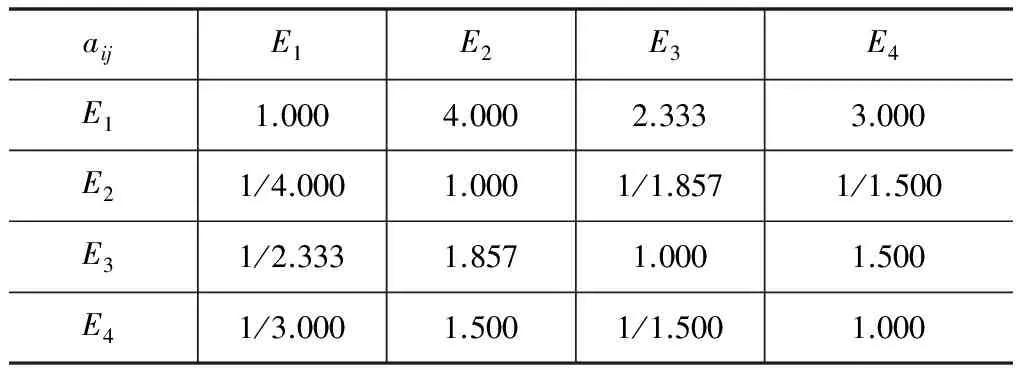
表4 第一层评价指标的两两对比判断矩阵
3 结束语
随着桥梁工程修建的饱和,桥梁加固逐渐成为研究热点。本文采用改进AHP法来确定了各评价指标的权重,具有较好的可靠性与可操作性,避免了传统层次分析法中标度不合理、判断矩阵难满足一致性的问题。通过结合灰色关联度法建立的桥梁加固方案优选模型能够较好的选择出最优加固方案,可为桥梁加固工程项目提供参考,具有一定的实际运用价值。
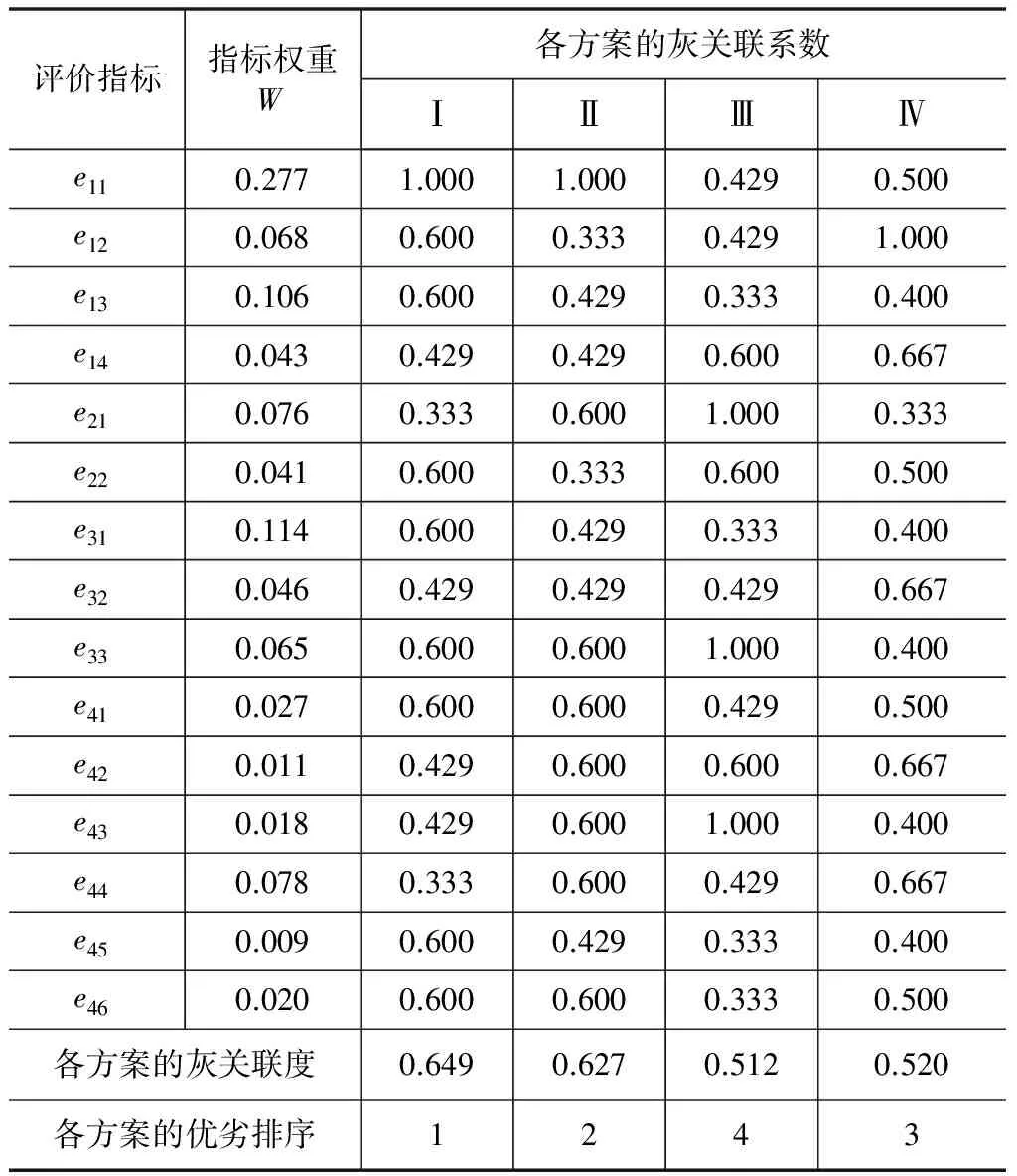
表5 灰色关联度法的评价结果
[1] 聂建国, 陶慕轩, 樊键生, 等.钢-混凝土组合结构在桥梁加固改造中的应用研究[J].防灾减灾工程学报,2010,30(S1):335-336.
[2] 边晶梅,朱浮声,高晓刚, 等.服役桥梁加固方案优选决策支持系统[J].中外公路,2009,29(2):156-161.
[3] 张鹏.桥梁加固方案的层次分析优选法[J].公路交通科技,2006,23 (7):92-95.
[4] 杨雅勋,李子春,李子青.基于组合权值灰关联法的旧桥加固方案评价[J].长安大学学报: 自然科学版版,2007,27(5):62-65.
[5] 边晶梅,朱浮声,白泉,等.组合赋权简化ELECTRE法优选桥梁加固方案[J].公路交通科技,2008,25(12):132-137.
[6] 徐泽水. 关于层次分析中几种标度的模拟评估[J]. 系统工程理论与实践,2000, 20 (7):58-62.
[7] 马云东,胡明东.改进的AHP法及其在多目标决策中的应用[J].系统工程理论与实践,1997(6): 40-43.
[8] 田民,刘思峰,卜志坤.灰色关联度算法模型的研究综述[J] .统计与决策,2008(1):24-27.
[定稿日期]2017-06-28
杨灯(1993~),男,研究生,研究方向为既有桥梁健全性评估。
U445.7+2
A
