Vectorial approximations of infinite-dimensional covariance descriptors for image classification

Jie-Yi Ren,Xiao-Jun Wu

©The Author(s)2017.This article is published with open access at Springerlink.com

Vectorial approximations of infinite-dimensional covariance descriptors for image classification

Jie-Yi Ren1,Xiao-Jun Wu1

©The Author(s)2017.This article is published with open access at Springerlink.com

The class of symmetric positive de finite(SPD)matrices,especially in the form of covariance descriptors(CovDs),have been receiving increased interest for many computer vision tasks.Covariance descriptors offer a compact way of robustly fusing different types of features with measurement variations.Successful examples of applying CovDs addressing various classification problems include object recognition,face recognition,human tracking,texture categorization,visual surveillance,etc.

As a novel data descriptor,CovDs encode the second-order statistics of features extracted from a finite number of observation points(e.g.,the pixels of an image)and capture the relative correlation of these features along their powers as a means of representation.In general,CovDs are SPD matrices and it is well known that the space of SPD matrices(denoted bySym+)is not a subspace in Euclidean space but a Riemannian manifold with nonpositive curvature.As a consequence,conventional learning methods based on Euclidean geometry are not the optimal choice for CovDs,as proven in several prior studies.

In order to better cope with the Riemannian structure of CovDs,many methods based on non-Euclidean metrics(e.g.,affine-invariant metrics,log-Euclidean metrics,Bregman divergence,and Stein metrics)have been proposed over the last few years.In particular,the log-Euclidean metric possesses several desirable properties which are beneficial for classification:(i)it is fast to compute;(ii)it de fines a true geodesic onSym+;and(iii)it comes up witha broad variety of positive definite kernels.

More recently, in finite-dimensional RCovDsbased methods have shown encouraging results in image classification,as opposed to low-dimensional RCovDs[1].It has been demonstrated that several types of Riemannian metrics for in finite-dimensional RCovDs can be computed with a mapping from the low-dimensional Euclidean space to a reproducing kernel Hilbert space(RKHS)and the corresponding Gram matrices. Normally, in finite-dimensional CovDs offer better discriminatory power than their low-dimensional counterparts. Nevertheless,all in finite-dimensional CovDs are rank-deficient because it is impossible to have an in finite number of observations in practice.Although this problem may,to some degree,be relieved by matrixregularization (adding a small perturbation to avoid matrix singularity),it prevents the utilization of Riemannian geometry directly.Moreover,the computational complexity of analyzing infinitedimensional CovDs is non-negligible.

Faraki et al.[2]used two specific feature mappings(random Fourier features and the Nyström method)for estimating in finite-dimensional CovDs,and derived resulting approximate in finite-dimensional CovDs as an alternative, to overcome the aforementioned issues.Motivated by this novel idea of estimating in finite-dimensional CovDs,we propose a method to obtain low-dimensional vectorial approximations of in finite-dimensional CovDs instead.We have two main contributions.Firstly,in contrast to the approximate in finite dimensional CovDs generated from estimated data of certain kernels based on Euclidean distance,our vectorial approximations are directly estimated from valid kernels based on Riemannian metrics.More specifically,the proposed approach estimates data on an RKHS of the Riemannian manifold rather than an RKHS of the original vectorial feature space and thus preserves the Riemannian geometry information of in finite-dimensional CovDs better.Secondly,the subsequent vectorial approximations are in a more compact form than the approximate in finite-dimensional CovDs.The proposed approach can be considered as a dimensionality reduction from in finite-dimensional CovDs to low-dimensional vectors. In addition,classical learning methods based on Euclidean geometry can be directly implemented without difficulties.We use the Nyström method to learn the feature mapping from the RKHS of in finite dimensional CovDs to a low-dimensional Euclidean space.With this feature mapping and valid kernels for in finite-dimensional CovDs,our approach not only preserves the intrinsic Riemannian geometry but also reduces the dimensionality,and is therefore better suited for classification.We have evaluated our approach on several standard datasets for image classification.Experimental results show the accuracy improvements of vectorial approximations over covariance approximations.Figure 1 shows the entire procedure of our approach and Faraki et al.’s approach[2].

1 Review of covariance descriptor

Region covariance matrices were introduced as a novel region descriptor for human face detection and classification.The process of generating CovDs from images is illustrated in Fig.2.The data matrixconsists ofnobservations extracted from an image sample,denoting theith observation.The CovDs is defined as

Assume we have an implicit mappingfromd-dimensional Euclidean space to the RKHSH,whose dimensionalitycould be considered as potentially in finite.With the mapped data matrixand Eq.(1),a CovDsCφin the RKHSis de fined as

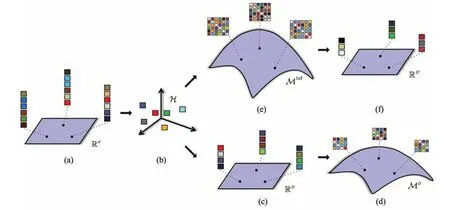
Fig.1 Conceptual comparison of our approach and Faraki et al.’s approach for image classification.Faraki et al.’s approach follows(a)–(d),(a) first mapping image features in low-dimensional Euclidean space to an in finite-dimensional Hilbert space(b)and then applying the Nyström method to learn a feature mapping from Hilbert space to another low-dimensional Euclidean space(c),which can be used to obtain the finite-dimensional approximations of in finite-dimensional CovDs(d).In contrast,the proposed approach follows the path(a)–(b)–(e)–(f)to learn a feature mapping from the Riemannian manifold of in finite-dimensional CovDs(e)to a new low-dimensional Euclidean space(f)to obtain the vectorial approximations.

Fig.2 Conceptual illustration of generating CovDs from images.F(x,y)is the feature vector at position(x,y)in the image sample,and is composed of information from different features such as intensity,gradient,Gabor wavelets,etc.

This type of data embedding into an RKHS is common in many applications and seems to lead to impressive results.However,the use of infinitedimensional CovDs is restricted in practice.Sincethe CovDsis always rank-deficient and thus may only be positive semi-de finite,with rank at mostn−1,which means it is on the boundary of the positive cone and at an in finite distance from any SPD matrices.In order to apply the theory ofSym+,regularization is applied asNow,is strictly positive and invertible,which are necessary for Riemannian metrics.

2 Vectorial approximations of CovDs

In this section,we present the proposed approach for obtaining vectorial approximations of infinitedimensional CovDs.The key idea is to estimate in finite-dimensional CovDs via valid kernels based on Riemannian metrics,resulting in low-dimensional vectors,to obtain better classification accuracy.Before delving into the detail,we start with a brief description of the metrics and corresponding kernels for CovDs.

2.1 Riemannian metrics

AnSPD matrixisa symmetric matrix with the property that all its eigenvalues are positive.As mentioned above,the space of SPD matrices is not a Euclidean space but a Riemannian manifold.Each point on the Riemannian manifold has a well-de fined continuous collection of scalar products de fined on its tangent space and is endowed with an associated Riemannian metric.A Riemannian metric makes it possible to define various geometric notions on the Riemannian manifold,such as angles,distances,etc.Since the manifold is curved,the distances specify the length of the shortest curve that connects the points,also known as geodesics.

Log-Euclidean metric.One of the most commonly encountered Riemannian metricsonSym+is the log-Euclidean metric,which results in classical Euclidean computations as

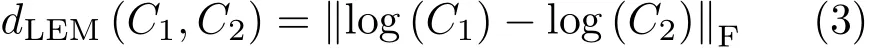
whereC1,C2∈Sym+,anddenotes the matrix Frobenius form.log(·)is the common matrix logarithm operator.The eigen-decomposition of a CovDsCis given byand the logarithm is calculated using logAs shown in Ref.[3],Sym+endowed with a log-Euclidean metric is also an inner product space,with inner productA broad variety of kernels can be developed.

Log-Hilbert–Schmidt metric.A generalization of the log-Euclidean metric on the Riemannian manifold of positive de finite matrices to the in finite dimensional setting is the log-Hilbert–Schmidt metric.It is applied in particular to compute distances between CovDs in an RKHS,for which explicit formulae and the inner product are obtained via the Gram matrices induced by an implicit mappingφand the corresponding positive de finite kernelK.LetX=be two data matrices,andare CovDs in the RKHSas de fined in Section 2.LetKx,Ky,andKx,ybe then×nGram matrices of the positive de finite kernelK.Letso thatLetNAandNBbe the numbers of nonzero eigenvalues of spectral decompositionsandThe log-Hilbert–Schmidt metric betweenis de fined as

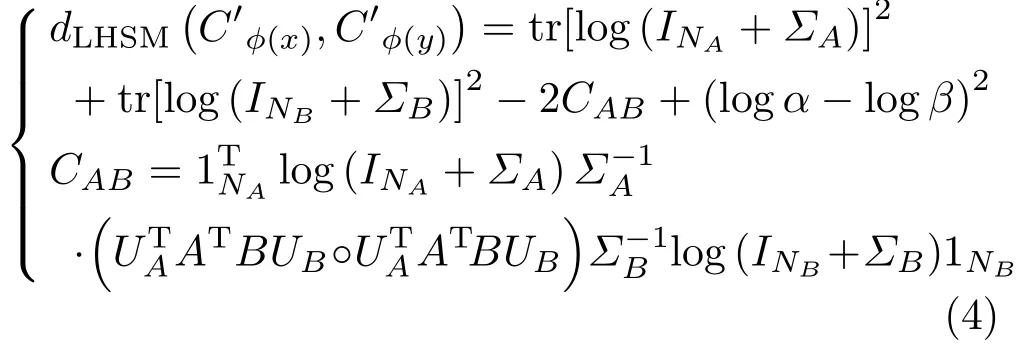
where°denotes the Hadamard(element-wise)product and the log-Hilbert–Schmidt inner product is defined as+(logα)(logβ).

2.2 Nyström method

The Nyström method was used in Ref.[2]for learning a feature mappingto obtain D×D in finite-dimensional CovDs estimates. Letbe the mapped data matrix de fined in Section 2, so thatIn other words,a rank D approximation of kernelcan be computed as ZTZ,Z=[Σ1/2V]. Σ and V are the top D eigenvalues and corresponding eigenvectors ofd ≤ D ≤ n.Estimates ofcan be obtained with the mapping ζ(·)by

The corresponding estimates of CovDs in H are obtained as

To achieve the aim of effective and compact in finite-dimensional CovDs estimation,we propose a revised scheme. Rather than kernels based on Euclidean distance,we use kernels based on Riemannian metrics to learn a mapping ζ′:Sym+→with the Nyström method. Given a setof m CovDs,we obtain a D′-dimensional vector representation by modifying Eq.(5)to

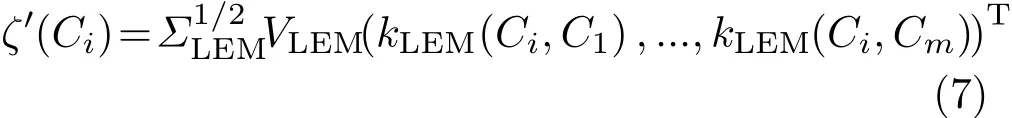
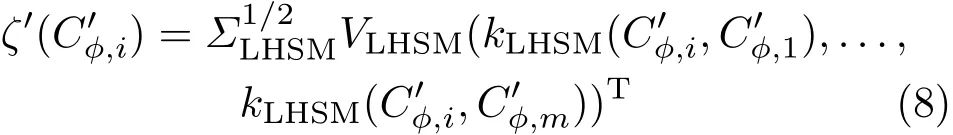
Obviously,we can extend this approach to estimate in finite-dimensional CovDs. Given a set of m in finite-dimensional CovDs,its D′-dimensional vectorial approximationcan be obtained as the same in Eq.(7)by and kLHSMis a valid kernel based on the log-Hilbert–Schmidt metric,ΣLHSMand VLHSMare the top D′eigenvalues and corresponding eigenvectors of the m×m kernel matrixD′≤ m. The process of estimating in finite dimensional CovDs using the Nyström method and kernels based on log-Hilbert–Schmidt metric is schematically represented in Algorithm 1.

3 Evaluation

The proposed approach has been evaluated on standard datasets for three image classification tasks: material texture categorization,virus cell identification,and human face recognition.Figure 3 shows image samples from different datasets.

3.1 Implementation details

In order to demonstrate the empirical performance of our approach, we compare the accuracy of low-dimensional CovDs,approximate in finite dimensional CovDs and vectorial approximations of in finite-dimensional CovDs with a simple nearest neighbor classifier,and we also provide classification results of partial least squares (PLS) basedtechniques.In particular,low-dimensional CovDs combined with kernelized PLS is similar to the method of covariance discriminant learning(CDL)[3],which can be considered as the state-of-the-art for CovDs-based classification.Different algorithms compared in our experiments are as follows:

?

•Cov·NNLEM:Low-dimensional CovDs with log-Euclidean metric based NN classifier.

•Approximate in finite-dimensional CovDs obtained by the Nyström method with log-Euclidean metric based NN classifier,which is the same as the method in Ref.[2]but replacing the affine-invariant metric with the log-Euclidean metric.

•Vectorial approximations of in finite-dimensional CovDs with Euclidean metric based NN classifier.

•Cov·KPLS: Low-dimensional CovDs with kernelized PLS.

•Approximate in finite-dimensional CovDs with kernelized PLS.

•Vectorial approximations of in finite dimensional CovDs with PLS.

Following standard practice[2],we extracted original features from each image sample and utilized a Gaussian kernel to generate in finite-dimensional CovDs.Gaussian kernels based on the log-Euclidean metric and log-Hilbert–Schmidt metric were adopted as valid Riemannian kernels for low-dimensional CovDs and in finite-dimensional CovDs respectively.All parameters and the target dimensionality were determined by cross-validation.All algorithms were performed with MATLAB software and a quad-core 3.0GHz CPU.

3.2 Material texture categorization

For the first task,we used the UIUC Material dataset[4],which contains 18 categories of materials taken in the wild.Each category has 12 images of various sizes with various geometric details included.For each pixel at coordinate(x,y)in an image sampleI,we extract a feature vector:

whereare the color intensities,followed by the magnitude of intensity gradients and the magnitude of Laplacians,and is the response of a 2D Gabor wavelet with orientationuand scalev.We setu=4,v=3 here,and therefore the dimensionality ofFx,yis 19.Following standard practice,we randomly chose half of the images from each category for training,and the rest were used for testing.This random selection procedure was repeated 10 times and the average classification accuracy with standard deviation is reported.

3.3 Virus cell identification

For this task,we used the Virus dataset[5],which contains images of 15 different virus classes.Each class has 100 segmented grayscale images,with a resolution of 41×41 pixels,all formed by transmission electron microscopy.We applied a similar setting as used for the previous dataset in Eq.(9),extracting 25-dimensional feature vectors at each pixel of an image to generate CovDs given by

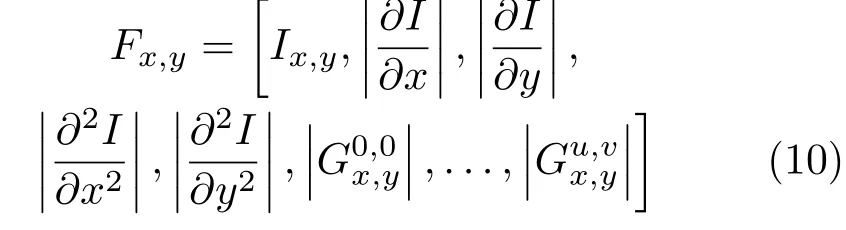
whereIx,yis the intensity and the 2D Gabor wavelet was used at 4 orientations and 5 scales here.We employed the original 10 splits provided by the Virus dataset and performed experiments with 9 splits for training and 1 split for testing. The average classification accuracy with standard deviation for all 10 gallery/probe combinations is reported.

3.4 Human face recognition

The last dataset we used is the FERET dataset[6].We selected the b subset of FERET dataset for evaluation,which comprises 200 persons,each having 7 images with expression and illumination variations.We again applied a similar setting as used for the previous dataset in Eq.(9),extracting 43-dimensional feature vectors with 5 orientations and 8 scales for 2D Gabor wavelets to generate CovDs given by

We randomly selected 3 images of each person for training and used the remaining images for testing,repeating the entire procedure 10 times.

3.5 Discussion of results

Tables 1–3 give the classification accuracies of all algorithms on these three datasets.As wecan see,the vectorial approximations,estimated from in finite-dimensional CovDs,are superior to low-dimensional CovDs and approximate in finite dimensional CovDs for all datasets,using the nearest neighbor classifier.The improvement of the vectorial approximations over the low-dimensional CovDs is up to 9.3%for these datasets,which is consistent with the claim that in finite-dimensional CovDs offer better discriminatory power over their low-dimensional counterparts. Our approach also out performs the method of Ref.[2]based on the log-Euclidean metric by at least 0.6%.We believe that estimating the in finite-dimensional CovDs with kernels based on proper Riemannian metrics can better reveal the intrinsic geometry than kernels based on a Euclidean metric,as the empirical results demonstrate.Interestingly,our approach even obtained comparable performance to more complicated kernelized PLS learning.With PLS,the classification accuracies of our vectorial approximations were slightly boosted to 47.7%±3.0% and79.4%±3.3% for UIUC and Virus datasets,respectively.This indicates that vectorial approximations are well-suited for CovDs-based classification.

Table 1 Classification accuracies for the UIUC Material dataset

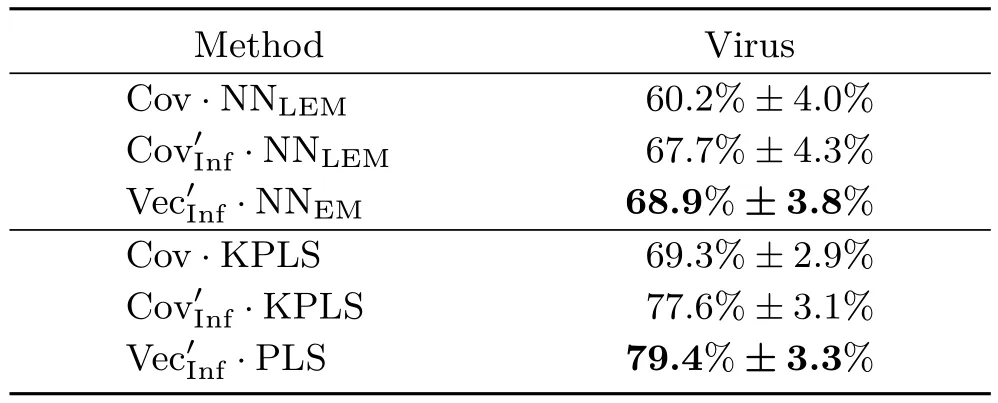
Table 2 Classification accuracies for the Virus dataset

Table 3 Classification accuracies for the FERET dataset

Acknowledgements

This work was supported in part by the National Natural Science Foundation of China(No.61373055).

[1]Harandi,M.;Salzmann,M.;Porikli,F.Bregman divergences for in finite dimensional covariance matrices.In:Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition,1003–1010,2014.

[2]Faraki,M.;Harandi,M.T.;Porikli,F.Approximate in finite-dimensional region covariance descriptors for image classification.In: Proceedings of the IEEE International Conference on Acoustics,Speech and Signal Processing,1364–1368,2015.

[3]Wang,R.;Guo,H.;Davis,L.S.;Dai,Q.Covariance discriminative learning: A natural and efficient approach to image set classification.In:Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition,2496–2503,2012.

[4]Liao, Z.; Rock, J.; Wang, Y.; Forsyth, D.Nonparametric filtering for geometric detail extraction and material representation.In:Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition,963–970,2013.

[5]Kylberg,G.;Uppström,M.;Sintorn,I.-M.Virus texture analysis using local binary patterns and radial density pro files.In:Progress in Pattern Recognition,Image Analysis,Computer Vision,and Applications.Martin,C.S.;Kim,S.-W.Eds.Springer,573–580,2011.

[6]Phillips,P.J.;Moon,H.;Rizvi,S.;Rauss,P.J.The FERET evaluation methodology for face-recognition algorithms.IEEE Transactions on Pattern Analysis and Machine IntelligenceVol.22,No.10,1090–1104,2000.

1School of IoT Engineering,Jiangnan University,Wuxi 214122,China.E-mail:J.-Y.Ren,alvisland@gmail.com;X.-J.Wu,xiaojunwu jnu@163.com

2017-02-27;accepted:2017-07-12

Jie-YiRenis currently a Ph.D.candidate in the School of IoT Engineering at Jiangnan University.His research interest is in computer vision and machine learning.

Xiao-Jun Wuis a professor in the School of IoT Engineering at Jiangnan University.He has his Ph.D.degree in pattern recognition and intelligent systems.He has published more than 150 papers on pattern recognition,computer vision,fuzzy systems,neural networks,and intelligent systems.

Open AccessThe articles published in this journal are distributed under the terms of the Creative

Commons Attribution 4.0 International License(http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use,distribution,and reproduction in any medium,provided you give appropriate credit to the original author(s)and the source,provide a link to the Creative Commons license,and indicate if changes were made.

Other papers from this open access journal are available free of charge from http://www.springer.com/journal/41095.To submit a manuscript,please go to https://www.editorialmanager.com/cvmj.