半潜式起重铺管船坐墩配墩优化设计与分析

王羲威，姜立群，刘广辉，李 勇，逄建涛

[海洋石油工程(青岛)有限公司，山东 青岛 266520]

0 引 言

深海海洋油气开发潜力巨大。近年来，我国船舶和海洋工业向深水发展，大型深水海洋工程建设项目需求也随之增多，其中深水半潜式起重铺管船以其稳性好、动力强、起重量大等优良性能，越来越受到海洋工程企业的关注。掌握深水半潜式起重铺管船的建造技术，显得尤为必要。

深水半潜式起重铺管船是在海上进行起重吊装作业和深水铺管作业的工程船舶，其建造要求高，涉及的技术复杂，需要设计配套与其建造技术相适应的工艺装备。先进的工艺装备对提高该类型船舶的制造工艺水平，提高机械化、自动化、智能化制造水平有重要意义。本文将主要概括介绍深水铺管船一项关键工艺装备的设计优化方法，即支撑垫墩的布置优化设计的方法。

1 概 述

该船舶底部模块左右两个浮体，单浮体宽度为35m，长度180m，单浮体平均单位重量为91t，分段在车间内制造，完成后下船坞组对，分段组对前提前布好支墩，支墩的布置原则为在保证船体建造安全和质量的前提下，尽量节省支墩材料，减少支墩的数量。该船型为平底船型，沿纵向中心线布置的支墩承载能力约为70%的船体重量，边墩承载能力约为25%船体重量，所以中部支墩布置较为密集，中墩与各边墩布置数量比例按照3∶1配置。

坞墩强度标准为试验得来的安全载荷。坐墩前要做试验，并对坞墩的强度进行校核，强度校核要求如下：(1)计算载荷应小于安全载荷；(2)承载能力为1.3倍计算载荷的垫墩应不少于总数的30%；(3)实际载荷小于安全载荷30%的垫墩应去掉，并重新进行优化计算。

船坞内支墩布置图如图1所示，共计划使用支墩300个。

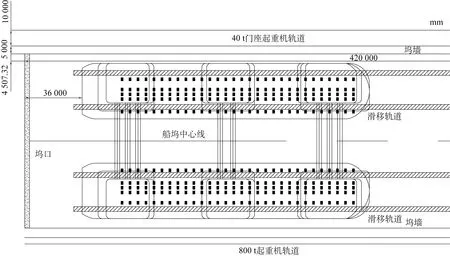
图1 支墩布置图Fig.1 Layout of docking block

2 深水半潜式起重铺管船坐墩配墩的设计及优化分析

2.1 坐墩支反力的计算

借助有限元法计算垫墩支反力。有限元法是一种常用的高效能数值计算方法。科学计算领域常常需要求解各类微分方程，而许多微分方程的解析解一般很难得到。使用有限元法将微分方程离散化后，可以编制程序，使用计算机辅助求解。

在具体设计计算的过程中，将垫墩和深水半潜式起重铺管船的下水支架看作具有一定刚性系数的弹性支座，将深水半潜式起重铺管船船体看作一根具有分布质量和抗弯刚度的薄壁空心梁。其力学模型为一根连续梁坐在一系列弹性支座上。之后用有限元法进行坐墩支反力计算。该种方法相较于传统的计算方法有明显的优势，其数据准备工作并不复杂，计算求解时间短，可以直接得到船体的弯曲变形和垫墩支反力，为后续垫墩支反力校核提供了较大的便利，数据结果精确、直观[1]。

2.2 坐墩配墩的布局及尺寸优化

深水半潜式起重铺管船坐墩配墩的布局及尺寸优化是指在目标船体尺寸和排水量确定的情况下，确定该船建造时垫墩的位置布局及墩木结构尺寸的最优方案，使垫墩的承载力足够，不致引起船体变形，且在此前提下用料最省。该优化程序采用分层优化的方法，通过外层优化计算，确定墩木的最优化位置，再通过内层优化计算，得出墩木的最优化尺寸[2]。其程序如图2所示。

图2 布墩及尺寸优化流程图Fig.2 Flowsheet of docking block position and size optimization

2.2.1垫墩的位置优化计算

借助遗传算法确定墩木的最佳位置。遗传算法通过模拟生物的遗传进化机制，通过计算机程序计算来求得一定客观条件下的复杂系统优化计算的最优解。规模50～100的群体，经过10～20代的进化模拟，遗传算法都能以高概率找到最优解或者近似最优解。应用于坐墩配墩则是在选择海洋石油工程(青岛)有限公司的场地作为建造深水半潜式起重铺管船场地的条件下，求得墩木布置的最优化方案。

设计计算方法如下。已知船体的尺寸、排水量等技术参数，设A≥B，A为墩木位置总个数，B为有效墩木位置的个数，首先将A个墩木进行编号，用1，2，3，……，A代表各个墩木的位置，从中选取B个有效墩木位置，经过计算机程序计算得到可行性方案的解集，进而择取其中用料最省的解对墩木位置进行优化设计。计算流程如图3所示。

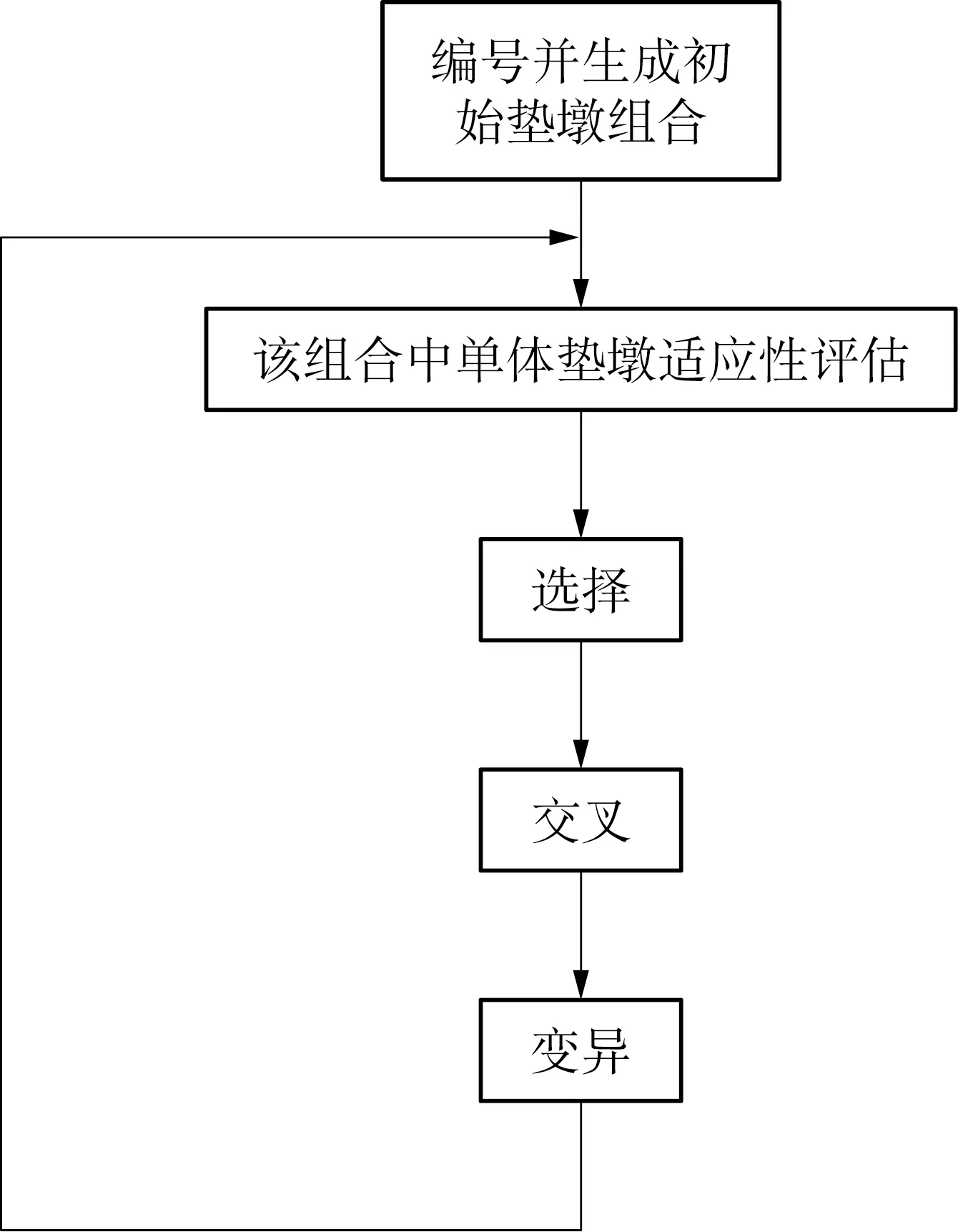
图3 垫墩位置优化遗传算法流程图Fig.3 Flowsheet of position optimization with genetic algorithm

2.2.2墩木尺寸的优化计算

在通过前述计算确定了垫墩位置的情况下，建立数学模型，再进行垫木尺寸的优化计算。该数学模型公式如下：

s.t.Gj(Xp,Xd)≤0,j=1,2,K,Ng,

(1)

式中：V*(XP)是给定垫墩位置XP的前提下，垫墩最小总体积；Xd是由4个墩木结构尺寸变量(墩木宽度Bi、墩木长度Ci、松木高度H1i、硬木高度H2i)构成的向量；Gj为设计必须满足的第j个约束的约束函数；Ng为约束条件的个数。确定数学模型之后利用序列二次规划方法求解该模型，得到符合条件的墩木总体积后回代到外层优化程序。内外两层程序循环优化计算，直至得到最优解[3]。

3 深水半潜式起重铺管船坐墩配墩的多目标优化设计

当目标函数由两个及以上独立的评价指标组成的时候，就可以用多目标优化方法求解。与单目标求最优解问题不同的是，多目标优化往往不存在最优解，而只能得到符合要求的解，所求得的通常为一个解集，而且目标函数越多求解的难度越大。常用的求解方法有约束法、线性加权和法、最大最小法、权值法、宽容排序法等。

单目标设计优化应用于船舶坐墩配墩是指在确定的船舶尺寸、排水量、垫墩位置条件下，求得垫墩总体积的最小值；而坐墩配墩的多目标设计优化还要求考虑船体尾部的强度储备[4]。

根据以上条件来考虑设计优化方法。将墩木总体积V(x1)和船尾结构强度储备作为目标函数，船尾典型结构的强度用船尾中内龙骨所受垫墩支反力之和F(x2)来表示，这样F(x2)越小则结构强度储备越大。采用宽容排序法求解，即根据上文描述的方法确定墩木的最佳位置和尺寸之后，在不改变墩木位置的前提下，重新选择墩木的总体积，使得船尾中内龙骨所受垫墩支反力之和R(x2)取得最小值，得到一系列符合要求的min{V(x1)，F(x2)}。再根据实际情况，取其中的某个解作为应用于方案的解，这样可以兼顾两个性能不同的指标，使坐墩配墩设计更为合理。

4 深水半潜式起重铺管船坐墩配墩的鲁棒设计

在进行坐墩配墩设计时，支墩所受的力与支墩的刚度、船体的重量及刚度、船体重量分布有关，而这些参数在进行坐墩配墩设计时难以确定。支墩组合刚度这种不确定的参量则可视为概率不确定性量。将船体梁载荷看作是非概率不确定性量，在此两种不确定性量同时存在的情况下求坐墩配墩方案的解[5]。

程序计算结果表明，在增加不确定性参数之后，支墩的总体积增加，相对于船体梁载荷不确定性的影响，支墩组合刚度的影响要更大一些。这也就启示设计人员要在设计的过程中更加重视支墩木材的树龄、湿度、使用破坏的情况等，要相应地留一定余量。

5 结 语

本文简要概述了用于深水半潜式起重铺管船坐墩配墩的设计优化的方法，介绍了墩木布局及尺寸优化设计的方法、多目标条件下的墩木设计优化的方法及存在不确定性量条件下的鲁棒设计的方法。采用以上方法，可以使得墩木布置得到优化配置，在保证建造安全和减少船体变形的前提下节省垫墩材料。

坐墩配墩的设计优化要求考虑船体尾部的强度储备，优化求解时要根据实际情况兼顾两个甚至多个性能不同的指标，使坐墩配墩设计更为合理，在实际设计过程中还要考虑到船体重量分布的不确定性，提前留有足够的余量。本文总结的内容有望用于指导将来项目中的实际应用。

[1] 程远胜,曾广武.船舶坐墩反力的分析计算[J].华中理工大学学报,1994,22(10)：68.

Cheng Yuan-sheng,Zeng Guang-wu.The calculation of blocks reaction during ship docking [J].J Huazhong Univ of Sci & Tech,1994,22(10)：68.

[2] 程远胜,曾广武.船舶坐墩配墩优化.中国造船,1995(1)：18.

Cheng Yuan-sheng,Zeng Guang-wu.Optimum disposition of wooden blocks during ship docking [J].Shipbuilding of China,1995(1)：18.

[3] 游建军.船舶坐墩配墩的优化设计[D].武汉：华中科技大学,2004.

You Jian-jun.Optimization of docking blocks [D].Wuhan：Huazhong University of Science & Technology,2004.

[4] 游建军,程远胜.船舶坐墩配墩多目标优化设计[J].华中科技大学学报(自然科学版)，2004,32(1)：25.

You Jian-jun,Cheng Yuan-sheng.Multi-objective optimization of docking blocks [J].J Huazhong Univ of Sci & Tech (Nature Science Edition),2004,32(1)：25.

[5] 程远胜,曾广武.考虑不确定性的船舶坐墩配墩优化[J].华中科技大学学报,2002,30(3)：33.

Cheng Yuan-sheng,Zeng Guang-wu.Optimization for block placement with uncertainty during ship docking [J].J Huazhong Univ of Sci & Tech (Nature Science Edition),2002,30(3)：33.