基于中心环绕滤波器检测的图像特征点匹配算法
2018-01-08孙增友段玉帅
孙增友,段玉帅,李 亚
(东北电力大学 信息工程学院,吉林 吉林132012)
基于中心环绕滤波器检测的图像特征点匹配算法
孙增友,段玉帅*,李 亚
(东北电力大学 信息工程学院,吉林 吉林132012)
针对传统图像匹配算法特征点检测稳定性和准确性差的问题,提出一种尺度不变性的基于中心环绕滤波器检测(SCFD)的图像特征点匹配算法。首先,构建多尺度空间,利用中心环绕滤波器检测图像在不同尺度下的特征点,采用Harris方法和亚像素插值获得稳定的特征点;其次,联合快速定向旋转二进制稳健基元独立特征(BRIEF)(ORB)算法确定特征点的主方向,构建特征点描述算子;最后,采用汉明距离完成匹配,通过最小平方中值(LMedS)定理和最大似然(ML)估计剔除误匹配点。实验结果表明,在尺度变化时,所提算法的匹配精度达到96.6%,是ORB算法的2倍;其运行时间是尺度不变特征变换(SIFT)的19.8%,加速鲁棒性特征(SURF)的28.3%。所提算法能够有效提高特征点检测的稳定性和准确性,在视角、尺度缩放、旋转、亮度等变化的情况下具有较好的匹配效果。
特征点匹配;尺度不变性;特征点检测;快速定向旋转二进制稳健基元独立特征;最小平方中值定理
0 引言
图像匹配的任务是建立两张图像中同一场景部分之间的对应,这在计算机视觉应用中是一个重要的问题,如目标检测[1]、图像索引[2]、视觉定位[3]和视觉导航[4]等方面。其中大部分应用都受到实时性和稳定性的限制,尤其是在视觉定位系统中,由于采集的图像来自于不同的时间,采集图像的视角不同,以及受到环境中光照和噪声的影响,拍摄图像的边缘轮廓会存在较大的差异,甚至图像会十分模糊、噪声干扰较大。因此设计出一种能够快速提取稳定的特征点,同时最大限度提高图像匹配准确度和抗干扰能力的算法具有重要意义。
图像匹配算法可以分为两类:基于灰度信息的匹配算法和基于特征的图像匹配算法[5-6]。基于灰度信息的匹配算法通过空间二维滑动模板进行匹配,运算过程简单,匹配精度高,但是算法运算量大,对噪声比较敏感。而基于特征的图像匹配中常用的图像特征包括点特征、线特征和边缘特征,其中图像特征点的提取过程受到噪声影响较小,同时对于灰度变化、图像变形和遮挡具有较强的抗干扰能力。经典的特征检测方法,如Moravec算法[7]和Harris算法[8],它们的特征点检测过程只是在单一的尺度上进行,容易受到噪声影响。Lowe[9]提出的尺度不变特征变换(Scale-Invariant Feature Transform, SIFT)算法,利用高斯函数构建尺度空间,对图像缩放、旋转、仿射变换保持不变性,但是由于采用了128维的描述算子,计算量较大,不适合应用在对实时性要求较高的图像匹配中。Ke等[10]利用主元分析法替换SIFT算法中的直方图,从而达到对SIFT描述符进行降维的目的,但是影响其特殊性和增加描述算子形成的时间使得增加的匹配速度性能毁于一旦。Bay等[11]提出了加速鲁棒性特征(Speeded Up Robust Features, SURF)描述符,SURF最大的特征在于采用了积分图像和哈尔特征的概念,缩短了程序的运行时间,但是因为采用64维的浮点型描述算子,要求大量的存储空间。Agrawal等[12]提出了中心环绕极值(Center Surround Extrema, CenSurE)算法,通过设计简单的双层滤波器来近似高斯拉普拉斯,提高了计算效率,但是由于采用的线性滤波器导致滤波器响应信号稀疏,在尺度变化和几何变化时特征点稳定性差。Rublee等[13]提出了快速定向旋转二进制稳健基元独立特征(Oriented fast and Rotated Binary Robust Independent elementary Features (BRIEF), ORB)算法。ORB算法是加速分割测试特征(Features from Accelerated Segment Test, FAST)和二进制稳健基元独立特征(BRIEF)描述符的结合和改进,具有很高的计算效率。但是FAST特征点不具备尺度不变性[14],在图像发生尺度变化的情况下,该算法的匹配精度会受到严重的影响。
基于尺度空间提取特征点的思想,本文提出一种尺度不变性的基于中心环绕滤波器检测(Scale-invariant Center surround Filter Detection, SCFD)的图像特征点匹配算法。该算法提出的特征检测子可以有效提高计算速度和准确性,同时具备尺度不变性;其次,联合ORB构建特征点描述算子;最后通过最小平方中值(LMedS)定理和最大似然(ML)估计方法对数据进一步求精。将本文算法与ORB、SIFT、SURF等算法进行性能对比分析,实验结果表明,本文算法能够有效提高特征点的稳定性和匹配精度。
1 图像特征点的检测
由于图像中的特征点不易受到环境中的噪声影响,在灰度变化、图像变形和遮挡时具有较强的抗干扰能力,故基于特征的图像匹配算法得到广泛应用。而常用的特征点检测方法(如Harris、FAST)在特征点检测过程中只是在单一的尺度上进行,特征点容易受到环境中光照强度、噪声、视角改变等的影响。通过构建尺度空间模型可以将单尺度信息纳入尺度不断变化的动态分析框架中,更容易获得图像本质特征。SIFT算法,通过构建高斯金字塔并在不同的尺度上查找关键点。但是,由于对原始图像不断进行隔点采样,较高层的特征相对于原始图像的精度较低,造成在金字塔的较高层特征点不能被准确地定位。为了提高特征点的稳定性和获取特征点准确的位置信息,本文采用稳定性和计算效率更高的中心环绕双层滤波器,由于该滤波器在所有的尺度和像素上计算滤波响应,所以提取的特征点具有较高精度。
因此,提出一种新的特征点检测方法。首先利用中心环绕双层滤波器近似高斯拉普拉斯算子构建尺度空间,计算原始图像中的每个像素点的中心环绕哈尔小波响应值,采用积分图像加速运算过程[12],然后利用非极大值抑制方法检测极值,最后通过Harris和子像素插值获得更加稳定的特征点。
1.1 构建尺度空间
在利用高斯差分函数近似代替高斯拉普拉斯函数的启发下,本文利用更为简单的中心环绕双层滤波器近似高斯拉普拉斯算子,从而达到简化计算的目的。图1显示了通用的中心环绕小波的块大小n。设双层滤波器的内核尺寸为(2n+1)×(2n+1),外核尺寸为(4n+1)×(4n+1),设In是内核权重系数,On是外核权重系数,因为要使得滤波器DC响应为零,权重系数应满足下面的等式:
On(4n+1)2=In(2n+1)2
(1)
对尺度空间进行归一化处理:
In(2n+1)2=In+1(2(n+1)+1)2
(2)

图1 中心环绕双层盒滤波器Fig. 1 Center-surround bi-level boxes filter
将尺度空间划分为四组,每组由四层组成。为了提高特征点的提取精度,不同于SIFT中下一组是在上一组进行降采样,而是在每一组中采用尺度递增的中心环绕滤波器和原始图像作卷积,可以获得一系列的响应图。为了进一步提高特征点的稳定性和匹配的准确性,通过行子像素插值精确定位特征点位置。在每一组中选择四层尺度图像,选择内核大小为3×3的滤波器作为尺度空间的初始层,通过放大滤波器的大小可以减小SIFT算法不断重复隔点采样过程带来的精度损失。为了确保滤波器的内核为奇数,并且能够检测到中心像素的出现,双层滤波器内核大小逐层增加2。为了能在3D邻域内确定极值点,需要多出两层,即初始层和顶层只作为比较用而并不包含极值点。滤波器大小的构造方法是:每组滤波器大小和步长依次增加,如第一组滤波尺寸大小分别为3、5、7、9。第二组每层滤波器内核依次增加4,内核大小依次为5×5、9×9、13×13、17×17,第三组、第四组等以此类推。图2给出了不同组下各层中心环绕双层滤波器内核大小。

图2 双层盒滤波器内核大小Fig. 2 Core size of center-surround bi-level boxes filter in different groups
1.2 非极大值抑制极值检测
计算不同尺度的滤波器在图像中每个像素上的响应值,滤波器响应的幅度给出了特征强度的指示,响应越强,特征点重复性越好。通过设置阈值滤除能量较弱以及错误定位的特征点,然后采用非极大值抑制检测尺度空间的极值点作为候选的特征点,将经过中心环绕双层滤波器处理的每个像素点与二维图像空间和尺度空间邻域内的26个点进行比较,初步定位特征点。
1.3 消除边缘响应
在边缘或者线段上容易产生不稳定的特征点,根据极值在横跨边缘的地方有较大的主曲率,而在垂直边缘的方向有较小的主曲率的特点,采用尺度自适应的Harris方法计算主曲率,剔除不稳定点的特征点。获取特征点滤波器响应函数的二阶距矩阵H,主曲率比通过H的迹与行列式比值计算得到,如式(3)所示:
(3)
其中:Lx和Ly为滤波器响应函数在x和y方向上的偏导;主曲率值比阈值设为10[9]。
1.4 子像素插值
离散空间的极值点并不是真正的极值点,为了获得精确的极值点位置,采用基于向量的正交性观测来实现亚像素角点定位[15]。采用子像素插值可以有效提高特征点的稳定性,获得更高的重复率。检测原理如图3所示。

图3 亚像素角点检测原理图Fig. 3 Principle diagram of subpixel corner detection
设p为像素级角点,q为角点的真实位置。DIpi表示在q的一个邻域点pi处的图像梯度,该梯度向量与pi和q组成的向量正交,ε表示两者正交程度。两者正交的程度误差εi=DIpiT(q-pi)。获取角点的亚像素位置等价于求以下函数的最小值:
f(q)=∑εi2=∑[DIpiT· (q-pi)]2
(4)
通过对f求偏导可得系统方程如下:
(5)

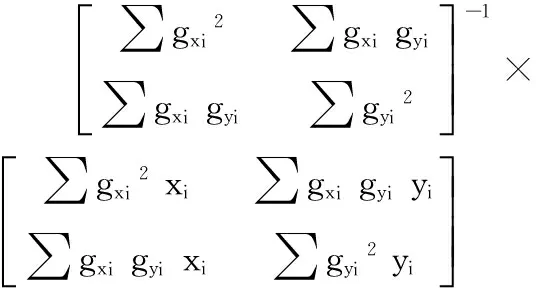
(6)
亚像素角点定位算法具体步骤如下:
步骤1 初始角点位置和窗口大小,计算窗口邻域内所有点在图像坐标系下的灰度信息以及位置信息。
步骤2 利用邻域点在图像中的位置信息计算邻域点的梯度信息。
步骤3 根据邻域点的位置和梯度信息通过上面的推导式(6)计算特征点的准确位置q。
步骤4 设定阈值D,通过式(6)计算出第i次检测到的特征点位置qi,并以此为中心计算相邻i+1次检测到的特征点位置qi+1误差,当两次计算得到的特征点误差满足|qi-qi+1| 为了确保特征矢量具有旋转不变性,需要为每个特征点分配一个主方向。利用灰度质心法[13]确定所有特征点的主方向。以特征点为中心、半径为r做圆,计算圆形邻域范围内的灰度质心位置。把中心位置和质心位置之间的偏移向量定义为该特征点的主方向。定义矩的计算公式如下: (7) 质心位置为: C=(m10/m00,m01/m00) (8) 主方向为: θ=arctan(m01/m10) (9) SIFT和SURF算法由于采用了维数较多的浮点型数据格式的描述符,不但降低了匹配效率,同时也使得内存开销增大。因此,本文联合ORB描述算子,在BRIEF的基础上加上旋转不变性,作为特征描述方法。 构造特征点描述符的具体步骤如下: 步骤1 对图像进行高斯滤波(方差为2,窗口大小为9×9)。以特征点为中心,选取大小为b×b的邻域窗口。在邻域窗口内随机选取两个点,通过比较像素点大小并进行二进制赋值,如下: (10) 其中:p(x)、p(y)分别是随机选取的点x=(u1,v1)、y=(u2,v2)的像素值。 步骤2 在邻域窗口中随机选取n对随机点,重复步骤1的二进制赋值操作,形成二进制串编码,也就是特征描述子。 (11) 步骤3 确定特征点的主方向。由特征点周围的2n个点(xi,yi),i=1,2,…,2n组成一个矩阵S: (12) 采用邻域方向θ和对应的旋转矩阵Rθ,构建S的校正矩阵Sθ:Sθ=RθS。其中: (13) 式中θ为所要求取的特征点主方向。 步骤4 解决描述子的区分性。为了减少Steered BRIEF方差的亏损,并减少二进制码串之间的相关性,使用了一种学习的方法来选择一个较小的点对集合。方法如下: 1)建立一个约3×105的关键点测试集,关键点数据取自PASCAL2006集中的图像。 binArray=[p1,p2,…,pM];pi∈{0,1} (14) 对3×105个关键点提取结束后,得到一个3×105×M矩阵。计算该矩阵的每个列向量的均值,并按列向量的均值重新排序,形成向量Q。 3)进行贪婪搜索。把向量Q中排在第一的测试集中的列向量放到矢量R中,并从测试集中移除该列向量;然后把Q中依次排序的测试与R中测试求相关,超过设定阈值则丢弃,反之放到R中;重复前面的步骤直到R中有256个测试,否则升高阈值,重新测试一次。 由于生成的特征点描述子是一个256 b的二进制编码。计算两个特征点的最近距离和次近距离,设定阈值,本文取0.8,采用汉明距离进行判决。利用第2章求得的描述子,任取K1、K2两个描述子: (15) 对汉明距离进行异或处理得到特征描述子的相似程度D(K1,K2): (16) 当两个描述子相似度大于阈值时,即大于80%时,判定是相同的特征点,这两个特征点匹配成功。 图像采集过程中容易受到光照和噪声等的影响,从而造成匹配错误。为了进一步提高特征点匹配的精确度,首先采用最小平方中值定理(Least Median Squares theorem, LMedS)方法[16]预先剔除误匹配,然后使用最大似然估计(Maximum Likelihood, ML)可以得到较好的匹配结果。文献[17]利用随机抽取一致性(RANdom SAmple Consensus, RANSAC)算法剔除图像中的误匹配点,理论上RANSAC算法可以剔除外点的影响,进而得到全局最优的参数估计。但是,RANSAC算法需要在每次迭代过程中都要分内点和外点,需要预先设定阈值;其次,RANSAC的迭代次数由运行周期决定,无法预知迭代的次数。 LMedS克服了RANSAC的两个缺点。LMedS从所有记录的样本中抽出N个样本子集,使用最小二乘法对每个子集计算模型参数和该模型偏差,LMedS中不需要预先设定阈值来区分内点和外点。选取N个样本子集中偏差最小的所对应的模型参数作为最终的模型参数估计。LMedS方法可以有效地剔除错误数据并估计误差协方差。 最后采用最大似然估计方法对数据进行进一步求精。最大似然估计通过给定的观察数据来评估样本集中相关概率密度函数的参数,对于匹配点具有较好的稳定性,在匹配点中可以获得理想的估计结果。 本文提出的匹配算法SCFD的流程如图4所示。 图4 SCFD 算法流程Fig. 4 Flow chart of SCFD algorithm 本文实验平台采用Intel Core i5 2450M、CPU2.5 GHz、内存4.0 GB的计算机,操作系统为Windows 7,开发环境为Microsoft Visual Studio 2012。 重复率作为特征检测性能的评价标准方法,可以用来评价特征点的稳定性,重复率越高说明提取的特征点越稳定[18]。本文使用Mikolajczyk提供的标准图像库(http://www.robots.ox.ac.uk/~vgg/research/affine/)中给定的图像数据集,计算不同变化下各个算法的重复率。重复率的定义如下: (17) 在图像视角和尺度变化下对本文算法和FAST、SURF、SIFT和进行了实验测评。图5为视角和尺度发生变化时四种算法的重复率。从图5(a)可以看出在视角变化的情况下,本文提出的中心环绕滤波检测特征的重复率要高于SURF和SIFT。图5(b)表明在尺度发生变化时,本文算法的特征重复率优于SURF和FAST,同时克服了FAST不具有尺度不变性的缺陷。本文算法对于较大的缩放中心环绕滤波检测特征重复率比SIFT稍微要差,这主要归因于中心环绕滤波器覆盖的尺度比SIFT要少,因此对于大规模变化尺度不变性较SIFT略差。 为了对本文提出的SCFD算法作出全面的评估,针对同一场景在尺度、旋转和光照发生变化的情况下,将所提算法与ORB、SIFT、SURF算法作对比实验。 4.2.1 尺度性能分析 采集室外环境下一张图片并对其进行尺度变化,用来验证本文提出的SCFD图像特征匹配算法是否具备尺度不变性。图像匹配结果如图6所示。从图6(a)可以看出,当图像发生缩放时,采用ORB算法可以提取出更多的特征点,主要归因于ORB采用的FAST角点检测,但是由于算法本身不具备尺度不变性,所以可以明显看出特征点匹配线段较为杂乱,尤其是图像中松树的树枝部分出现很多错误匹配。图6(b)、图6(c)和图6(d)分别为SIFT、SURF和本文提出的算法的匹配结果,从图中可以看出均无明显的匹配错误。图6(d)为本文算法在尺度变化下的匹配结果,由于LMedS和最大似然估计方法剔除一部分误匹配点,使得匹配点减少,但是仍然保持大量的正确匹配对,满足匹配要求。 图5 视角和尺度变化下的重复率曲线Fig. 5 Repeatability curve under change of angle of view and scale 图6 尺度变化时不同算法图像匹配结果对比Fig. 6 Comparison of image matching results for different algorithms under scale change 为了进一步验证四种算法在尺度变化时的匹配性能,统计实验中的四组数据,如表1所示。由表1可以看出,在尺度发生变化的情况下,本文算法匹配精度为96.6%,比ORB提高了49.8个百分点,该算法在匹配性能方面的性能表现表明该算法具备尺度不变性;同时,本文算法的匹配精度比SIFT和SURF分别提高了1.3个百分点和5个百分点,这主要得益于本文提出的提纯算法能够有效剔除图像中的不稳定的特征点,提高了匹配性能。 表1 尺度变化时不同算法图像匹配性能对比Tab. 1 Comparison of image matching performance for different algorithms under scale change 4.2.2 旋转性能分析 图7给出了在旋转变化条件下的不同算法的图像匹配对比结果。从图7(a)可以看出ORB算法具有一定的旋转不变性,但是在图像左上角的松树的松叶和走廊的轮廓部分会出现杂乱的特征点匹配线;图7(c)为SURF算法在旋转变化下的匹配结果,可以看出在图像的中间部分和地面部分存在明显的错误匹配;图7(c)和图7(d)分别为SIFT算法和本文所提算法在旋转变化下的匹配结果,从图中可以看出这两种算法的特征点匹配线段均比较平整,具有较好的匹配效果。 表2给出了在旋转变化条件下统计的不同算法的匹配数据。由表2可知,本文所提算法匹配精度达到了约98.0%,比ORB算法提高了10.9个百分点,较SURF提高了3.6个百分点。实验结果表明本文算法在旋转性能上表现出良好的匹配性能。 表2 旋转变化时不同算法图像匹配性能对比Tab. 2 Comparison of image matching performance for different algorithms under rotation change 4.2.3 光照性能分析 采用Mikolajczyk提供的标准图像库中的一组图像集leuven进行测试,图像大小为900×600,图像集中有6幅图片,图片亮度随着图像序号增加逐渐变暗。图8显示了不同程度光照条件下四种算法的特征点匹配精度。 由图8可以看出,在亮度发生变化的条件下,本文提出的SCFD算法的匹配精度要高于ORB、SIFT和SURF算法,在光照发生较大变化的情况下仍能取得较好的匹配效果,表明该算法具有良好的匹配精度和稳定性。这主要得益于该算法采用亚像素插值的方法确定特征点的准确位置,进一步增强了特征点的鲁棒性,同时采用的最小平方中值定理结合最大似然估计算法和仅采用汉明码匹配相比,可以有效地剔除外点,提高特征点匹配的准确性。 图7 旋转变化时不同算法图像匹配结果对比Fig. 7 Comparison of image matching results for different algorithms under rotation change 图8 亮度变化时不同算法图像匹配结果对比Fig. 8 Comparison of image matching results for different algorithms under brightness variation 为了验证本文提出的误匹配点剔除算法的性能,采用Mikolajczyk提供的标准图像库中的图集,在尺度变化、旋转变化和亮度变化下的条件下,利用该算法对SIFT、SURF和ORB进行提纯操作并统计其匹配精度数据,结果如表3所示。 从表3中的实验结果可以看出,本文提出的误匹配点剔除算法可以有效地对特征点数据进行提纯,提高了算法的匹配精度。 表3误匹配点剔除时不同算法匹配精度对比% Tab. 3 Comparison of matching accuracy for different algorithms under culling false matching points % 算法原匹配精度提纯后匹配精度SIFT95.798.5SURF92.396.8ORB74.480.4 为了验证本文所提算法SCFD对实时性的影响,统计在尺度变化、旋转变化和亮度变化下不种算法的运行时间。总的耗时分为特征点检测描述和匹配两部分,统计结果如表4所示。 表4 不同算法不同条件下运行时间对比 msTab. 4 Comparison of running time for different algorithms under different conditions ms 由表4可知,本文算法的平均耗时为706 ms,是SIFT算法的19.8%、SURF算法的28.3%,ORB平均耗时最少为217 ms。从表4可以看出,本文算法耗时较SIFT和SURF少,这主要归因于中心环绕滤波器检测的效率较高;另一方面由于采用了具有方向的二进制鲁棒性独立基本特征作为特征描述符,使算法实时性得到提高。同时因为:1)特征点检测提取过程在构建的多尺度空间上进行;2)匹配过程中增加了误匹配点剔除过程,本文算法耗时比ORB要多。从上述实验可以得出,本文算法在尺度变化、旋转变化和亮度变化下具备良好的匹配效果,满足实时性需求。 针对传统图像匹配算法特征点检测稳定性和准确性差的问题,本文提出了一种新的基于中心环绕滤波器检测的图像特征点匹配算法,通过构建多尺度空间,利用中心环绕双层滤波器检测图像在不同尺度下的特征点,使得特征点具备尺度不变性,并通过子像素插值获得更加稳定的特征点,然后联合ORB算法确定特征点主方向并构建特征点描述符,最后采用LMedS和最大似然估计剔除误匹配点。通过实验验证,本文所提算法在尺度、旋转、亮度等变化的情况下均取得理想的匹配效果,具有较高的稳定性和匹配精度。该算法在很大程度上提高了实时性,但其计算速度比ORB要慢,下一步的工作重点是进一步提高特征点匹配速度。 References) [1] SINHA S N, FRAHM J M, POLLEFEYS M. Feature tracking and matching in video using programmable graphics hardware [J]. Machine Vision and Applications, 2011, 22(1): 207-217. [2] ZHOU W, LI H, HONG R, et al. BSIFT: towards data-independent codebook for large scale image search [J]. IEEE Transactions on Image Processing, 2015, 24(3): 967-979. [3] CUMMINS M, NEWMAN P. Appearance-only SLAM at large scale with FAB-MAP 2.0 [J]. International Journal of Robotics Research, 2011, 30(9): 1100-1123. [4] ALONSO I P, LLORCA D F, GAVILAN M, et al. Accurate global localization using visual odometry and digital maps on urban environments [J]. IEEE Transactions on Intelligent Transportation Systems, 2012, 13(4): 1535-1545. [5] 高晶,吴育峰,吴昆,等.基于角点检测的图像匹配算法[J].仪器仪表学报,2013,34(8):1717-1725.(GAO J, WU Y F, WU K, et al. Image matching method based on corner detection [J]. Chinese Journal of Scientific Instrument, 2013, 34(8): 1717-1725.) [6] 杨晓敏,吴炜,卿粼波,等.图像特征点提取及匹配技术[J].光学精密工程,2009,17(9):2276-2282.(YANG X M, WU W, QING L B, et al. Image feature extraction and matching technology [J]. Optics and Precision Engineering, 2009, 17(9): 2276-2282.) [7] MORAVEC H P. Rover visual obstacle avoidance [C]// Proceedings of the 1981 7th International Joint Conference on Artificial Intelligence. San Francisco, CA: Morgan Kaufmann, 1981: 785-790. [8] HARRIS C G, STEPHENS M J. A combined corner and edge detector [C]// Proceedings of the 4th Alvey Vision Conference. Manchester, England: [s.n.], 1988: 147-151. [9] LOWE D G. Distinctive image features from scale-invariant keypoints [J]. International Journal of Computer Vision, 2004, 60(2): 91-110. [10] KE Y, SUKTHANKAR R. PCA-SIFT: a more distinctive representation for local image descriptors [C]// Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision & Pattern Recognition. Piscataway, NJ: IEEE 2004: 506-513. [11] BAY H, TUYTELAARS T, VAN GOOL L. SURF: speeded up robust features [C]// Proceedings of the 9th European conference on Computer Vision. Berlin: Springer, 2006: 404-417. [12] AGRAWAL M, KONOLIGE K, BLAS M R. CenSurE: center surround extremas for realtime feature detection and matching [C]// Proceedings of 2008 10th European Conference on Computer Vision, LNCS 5305. Berlin: Springer, 2008: 102-115. [13] RUBLEE E, RABAUD V, KONOLIGE K, et al. ORB: an efficient alternative to SIFT or SURF [C]// Proceedings of the 2011 IEEE International Conference on Computer Vision. Piscataway, NJ: IEEE, 2011: 2564-2571. [14] 白雪冰,车进,牟晓凯,等.结合快速鲁棒性特征改进ORB的特征点匹配算法[J].计算机应用,2016,36(7):1923-1926.(BAI X B, CHE J, MU X K, et al. Improved feature points matching algorithm based on speed-up robust feature and oriented fast and rotated brief [J]. Journal of Computer Applications, 2016, 36(7): 1923-1926.) [15] 谭晓波.摄像机标定及相关技术研究[D].长沙:国防科学技术大学,2004:30-34.(TAN X B. Study on camera calibration and its correlation technique [D]. Changsha: National University of Defense Technology, 2004: 30-34.) [16] ROUSSEEUW P J. Least median of squares regression [J]. Journal of the American Statistical Association, 1984, 79(388): 871-880. [17] 佘建国,徐仁桐,陈宁.基于ORB和改进RANSAC算法的图像拼接技术[J].江苏科技大学学报(自然科学版),2015,29(2):164-169.(SHE J G, XU R T, CHEN N. Image stitching technology based on ORB and improved RANSAC algorithm [J]. Journal of Jiangsu University of Science and Technology (Nature Science Edition), 2015, 29(2): 164-169.) [18] MIKOLAJCZYK K, SCHMID C. A performance evaluation of local descriptors [J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2005, 27(10): 1615-1630. SUNZengyou, born in 1963, professor. His research interests include signal and image processing, wireless communication. DUANYushuai, born in 1991, M. S. candidate. His research interests include image processing, pattern recognition. LIYa, born in 1992, M. S. candidate. Her research interests include signal and image processing, pattern recognition. Imagefeaturepointmatchingalgorithmbasedoncentersurroundfilterdetection SUN Zengyou, DUAN Yushuai*, LI Ya (SchoolofInformationEngineering,NortheastElectricPowerUniversity,JilinJilin132012,China) Aiming at the problems of poor stability and accuracy of feature point detection in traditional image matching algorithms, a new image feature point matching algorithm based on Scale-invariant Center surround Filter Detection (SCFD) was proposed. Firstly, a multi-scale space was constructed, a center surround filter was used to detect feature points of a image at different scales, Harris method and sub-pixel interpolation were applied to acquire the stable feature points. Secondly, Oriented fast and Rotated Binary Robust Independent Elementary Feature (BRIEF) (ORB) algorithm was combined to confirm the main direction of feature points and construct the description operator of feature points. Finally, Hamming distance was used to complete the matching, Least Median Squares (LMeds) theorem and Maximum Likelihood (ML) estimation were used to eliminate wrong matching points. The experimental results show that, the matching precision of the proposed algorithm is up to 96.6%, which is 2 times of that of the ORB algorithm when the scale changes. The running time of the proposed algorithm is 19.8% of that of Scale Invariant Feature Transform (SIFT) and 28.3% of that of Speed-Up Robust Feature (SURF). The proposed algorithm can effectively improve the stability and accuracy of feature point detection, and has better matching effects under the circumstances of different angle of view, scale scaling, rotation change and brightness variation. feature point matching; scale invariance; feature point detection; Oriented fast and Rotated Binary Robust Independent Elementary Feature (BRIEF) (ORB); Least Median Squares (LMedS) theorem 2017- 06- 05; 2016- 09- 08。 孙增友(1963—),男,吉林吉林人,教授,主要研究方向:信号与图像处理、无线通信; 段玉帅(1991—),男,河南商丘人,硕士研究生,主要研究方向:图像处理、模式识别; 李亚(1992—) 女,河南郑州人,硕士研究生,主要研究方向:信号与图像处理、模式识别。 1001- 9081(2017)12- 3547- 07 10.11772/j.issn.1001- 9081.2017.12.3547 (*通信作者电子邮箱sunzengyou@163.com) TP391.4 A2 特征点描述符
2.1 计算特征点主方向
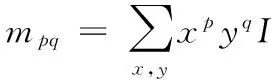
2.2 特征点描述符生成
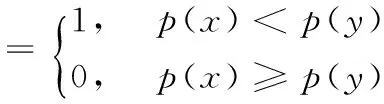


3 匹配算法
3.1 特征点匹配
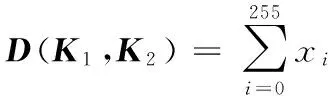
3.2 误匹配点剔除
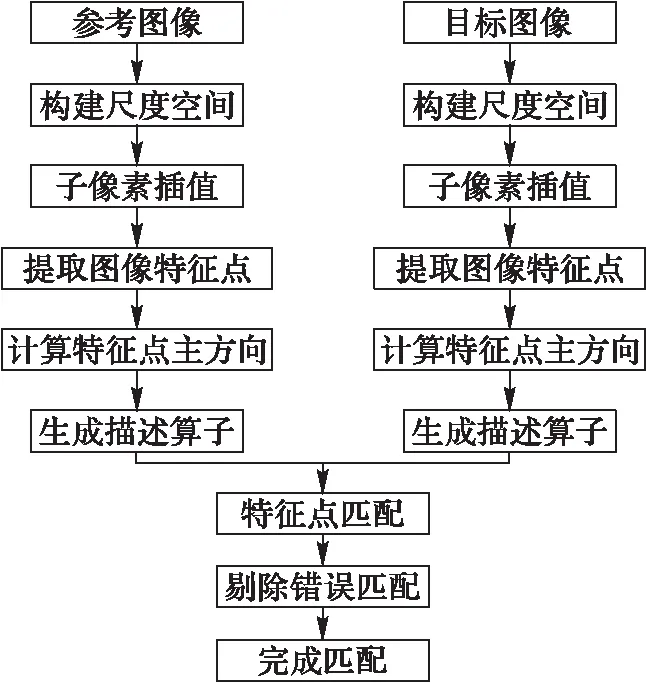
4 实验结果分析
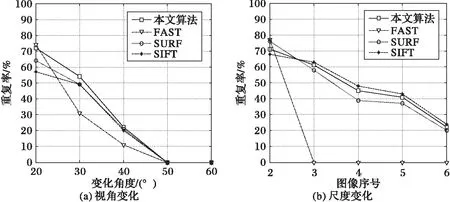
4.1 特征检测重复率实验
4.2 算法性能实验分析

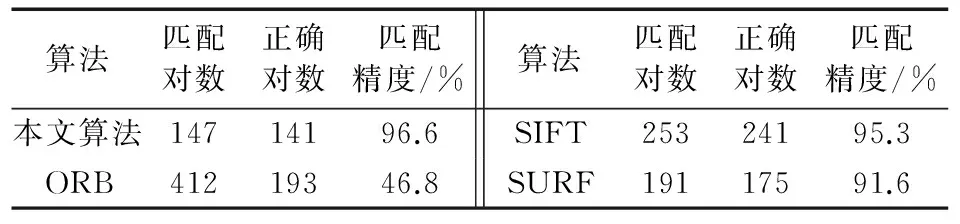



4.3 误匹配点剔除算法性能分析
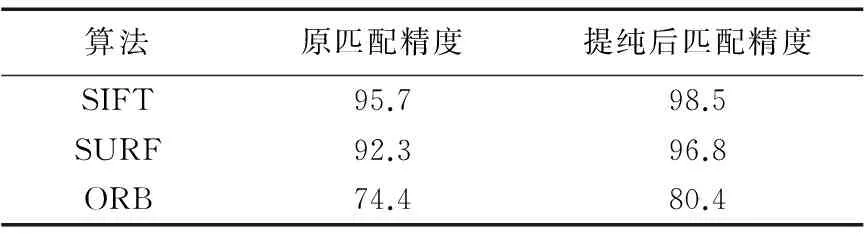
4.4 算法运行时间分析

5 结语
