模糊聚类遗传算法在军事装备物流中心选址中的应用①
2018-01-08吕学义郑绍钰
吕学义,郑绍钰
1(装备学院 研究生管理大队,北京 101416)
2(装备学院 装备采办系,北京 101416)
模糊聚类遗传算法在军事装备物流中心选址中的应用①
吕学义1,郑绍钰2
1(装备学院 研究生管理大队,北京 101416)
2(装备学院 装备采办系,北京 101416)
在分析军事装备物流中心选址问题基础上,构建了模糊聚类和遗传算法的混合算法模型,核心技术是把模糊聚类网络模型融合到遗传算法种群构建中,可以有效地避免遗传算法易出现早熟的现象,验证了算法具有很好的鲁棒性和可信度,仿真结果能够为决策者科学正确的选址提供一定的参考.
模糊聚类; 遗传算法; 选址
军事装备物流中心作为平战一体的物资保障单位,直接目的是保障军事行动的最终胜利. 这一点和地方物流以成本或是服务水平为目标明显不同. 军事装备物流中心具有较高的保密性,主要功能是满足平时与战时诸军兵种联合保障需求,其选址往往决定着物资的配送效率和配送方式,而选址的具体位置一旦被确定,往往难以改变,因此需要找到一个全局最优的地理位置. 一般说来,军事装备物流中心选址模型是一个非凸和非光滑的带有复杂约束的非线性规划模型难题[1].模糊聚类遗传算法非常适合用于解决非线性规划模型,它不仅是借鉴生物的适者生存规则和遗传进化机制相结合开发出的一种高效全局寻优搜索方法,而且优化计算时不依赖梯度信息或其他辅助知识,只需要影响搜索方向的目标函数和适应度函数,特别适合研究解决一些大型、复杂非线性系统的最优化问题,对目标函数的凸(凹)性、连续性、线性都没有限制,因此它是解决选址问题的一种比较理想方法.
1 模糊聚类遗传算法基本思想
在军事物流中心选址问题上,因军事需求多元化、政治、经济、地理和人文等方面决定了选址高度的复杂性,该中心选址作为带有强约束性的非线性规划模型,仅仅采用模糊聚类算法非常容易陷入局部优化值,得不到全局的最优解. 模糊聚类算法模糊聚类遗传算法基本思想是利用该算法使群体中的每个个体快速趋向于各自的极值点,通过遗传算子摆脱个体可能陷入的局部最优解,重复进行这样的搜索,直到找到最优解. 对于该模型的理解,具体可分为两个方面: (1)模糊聚类(Fuzzy clustering,FC)是用来快速估计样本数据中聚类个数和聚类中心位置的单次算法[1]. 在装备物资集中采购中心选址问题中,它将每个已知物资中心地址作为可能的聚类中心,并依据各个样本数据周围信息量的密度来估计该位置作为聚类中心的可能性.它能够非常快的估计出具体位置的聚类个数和聚类中心,并按照每一个坐标聚类的模糊联系程度自动地划分规则,使规则的数目降为最低而数据的行为达到最好. 在选址问题上,需要综合衡量的因素很多,具有多个复杂的非线性影响因素,这样数学模型中规则的数目将急剧增加,经常出现指数式增长问题,系统显得庞大而不易理解. (2)遗传算法 (Genetic algorithm,GA)是受到生物免疫系统的启发,在免疫学理论基础上发展起来的一种新的智能计算方法[2]. 主要是采用群体搜索策略,注重群体之间的信息交换,经过“初始种群产生—评价标准计算—种群之间个体信息交换—产生新的种群”循环过程,最终以大概率胜出获得最优解. 但在使用遗传算法求解问题的时候,会出现得到的近似最优解与最优解相差很大的情况. 这是因为遗传算法陷入了局部最优解,很难跳出局部最优解. 很多学者做过改进遗传算法方面的工作[3].
2 选址问题求解
选址问题种类多而且求解比较困难,不同的问题需要采用不同的优化求解方法,主要包括精确算法和启发式算法[4-8]. 本文中研究类型属于离散选址问题,可以选用遗传算法实现优化求解. 下面,分两个部分分别研究.
2.1 减法聚类分析讨论
为不失一般性,假设空间为M维,x1,x2,···,xn为n个样本数据,设样本数据已归一化到超立方体,因为每个样本数据都可能是聚类中心,所以样本数据的密度指标可具体表示为:

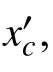
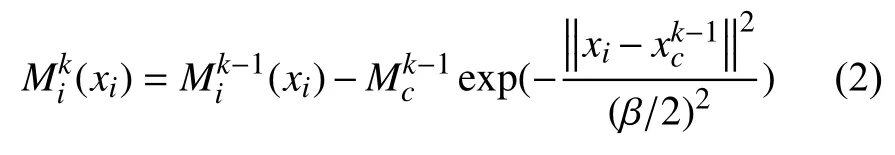
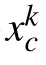
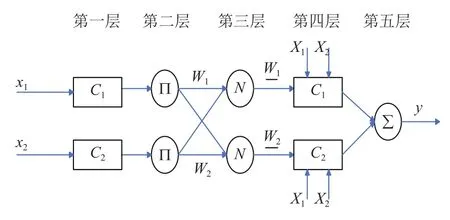
图1 模糊聚类网络结构
SCANFIS共分为5层,前3层为规则前件层,后2层为规则后件层. 具体结构说明如下:

第二层: 规则推理层,计算规则强度,这里的规则强度等于输入向量X对应聚类Ci的隶属度O2.

第三层: 这一层的每个单元以符号“N”标注,其作用是把各条规则的激励强度进行归一化处理,第i条规则归一化的激励强度是该条规则的激励强度与所有规则的激励强度之和的商.
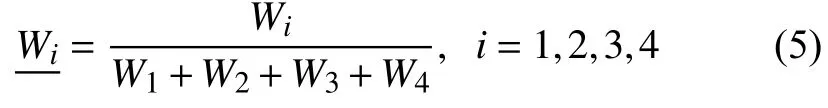
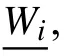
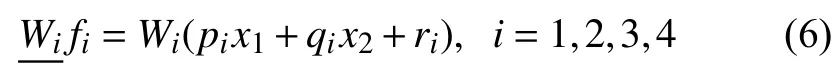
第五层: 输出层以符号“∑”标注,总输出为:
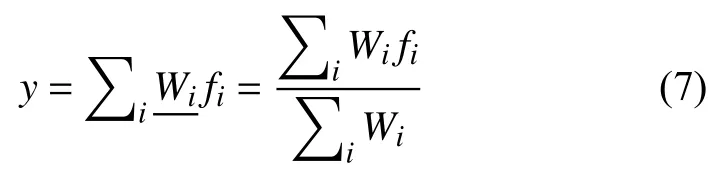
构建模糊聚类网络模型主要有四个步聚: (1)选取样本数据和验证样本数据; (2)将样本数据进行聚类分析,建立 SCANFIS 初始模糊模型; (3)假定 SCANFIS训练参数,确定算法,训练网络模型; (4)检验得到的模糊神经网络模型性能. 减法聚类的函数实现,通过上面分析讨论,主要通过Matlab7.1软件平台调用函数实现.
归纳起来,模糊聚类算法具有以下几个缺点: 一是处理有噪声样本数据集时,噪声数据对聚类结果影响较大; 二是聚类算法是一种无监督式的,在确定聚类数C的方法上还不是很完善; 三是模糊聚类算法对样本数据总是划分为C个类中心,导致聚类的有效性分析是离散的粒子状态.
2.2 模糊聚类遗传算法模型设计
模糊聚类遗传算法主要是利用遗传算法的全局收敛性及模糊聚类强大的局部寻优能力,对初始种群进行聚类,将得到新聚类中心作为选址模型,算法中还采用自适应交叉和变异概率,进一步增强算法的局部搜索性能.
模糊聚类遗传算法具体实施步骤: 第一步,按照编码规则产生初始种群,实质是在问题的解空间与算法的搜索空间之间建立一个映射; 第二步,种群中的各个染色体进行个体适应度值计算; 第三步,利用遗传算子进行GA进化; 第四步,以各个体为中心进行一次模糊聚类,对种群进行重新划分,并根据重新划分的种群集合进行重新聚类,得到新的聚类中心,作为新个体替换原有的种群个体; 第五步,按照一定的交叉概率进行交叉操作; 第六步,按照一定的变异概率进行变异操作;第七步,将子代染色体于父代染色体进行合并,得到一个临时种群; 第八步,判断算法是否结束,如果没有,则返回步骤二继续计算,否则,输出适应度值最优的计算结果. 具体模糊聚类遗传优化算法的流程,如图2所示.
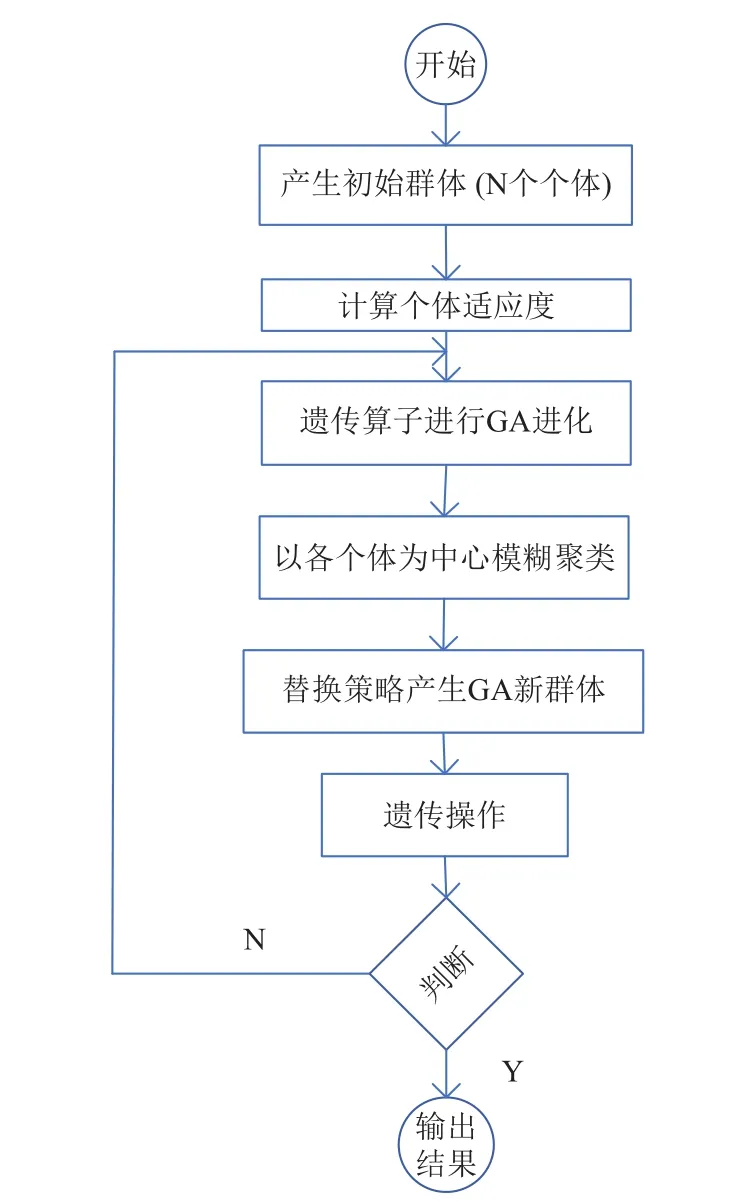
图2 模糊聚类遗传算法流程
在遗传算法中,通过编码组成初始群体后,遗传操作的任务就是对群体的个体按照其对环境的适应度施加操作,实现优胜劣汰的进化目的[9]. 遗传操作主要包括选择算子、交叉算子和变异算子.
(1)选择算子. 目前常用的选择算子有适应度比例方法、随机遍历抽样法和局部选择法等,本文选择一种最简单和常用的轮盘赌选择法,在该方法中,各个个体的选择概率和其适应度值成比例. 设群体大小N,其中个体i的适应度为f(i),则i被选中的概率为:
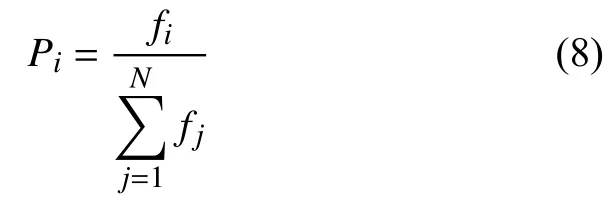
(2)交叉算子. 最常用的交叉算子为单点交叉. 具体操作是: 在个体串中随机设定一个交叉点,实行交叉时,该点前后的两个个体的部分结构进行互换,并生成两个新个体. 比如,个体A: 0011011; 个体B: 1010101,在第四位进行交叉时,生成的新个体为:A1: 0011101和B1: 1010011.
(3)变异算子. 基本内容是对群体中的个体串的某些基因座上的基因值作变动,分为实值变异和二进制变异. 一般来说,变异操作分两步完成: 一是对群中所有个体以事先设定的编译概率判断是否进行变异; 二是对进行变异的个体随机选择变异位置进行变异. 通常取值在0.001到0.01之间.
遗传算法中,交叉算子因其具有全局搜索能力而作为主要算子,变异算子因其局部搜索能力而作为辅助算子,通过交叉和变异相互配合又相互竞争的操作,使其具备兼顾全局和局部的均衡搜索能力.
3 选址模型构建
军事装备物流中心选址模型是非凸和非光滑的带有复杂约束的非线性规划模型,在构建中心模型时,先明确如下假设: (1)中心容量总是可以满足所属单位的需求量,并由该中心保障供应的所有单位的需求量确定; (2)一个需求单位仅由一个集中物流中心保障供应;(3)不考虑装备物资生产厂家到物流中心的运输费用.基于以上三条假设建立模型. 目标函数是各个采购中心到需求点的以需求量为权重的距离之和最小,目标函数模型如下所示:
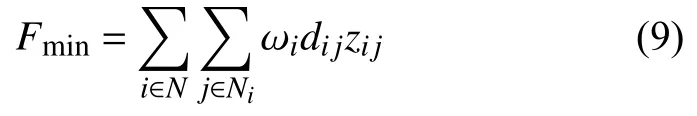
约束条件为:
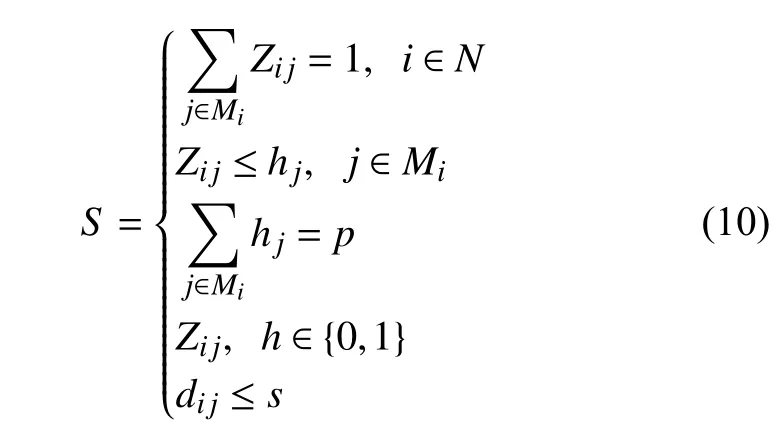
4 实例验证
假设,某部拟选址建立一个军事装备物流中心,实现平时和战时装备物资保障一体化,可以同时为武汉、无锡、桂林、西宁、沈阳和郑州六个联勤保障基地和中心供应战备物资,考虑到武汉作为联勤保障基地,要求新建的军事装备物流中心应充分考虑该基地所在的地理位置. 经了解,每个联勤保障单位每日运输需求量见表1,六个联勤保障单位的地理位置由实地测量得出. 政策支持,通过15-25位领域专家咨询得出,量化后的数据值1-10之间,数值越大表明支持越大.为简便起见,设每单位运费为1元.
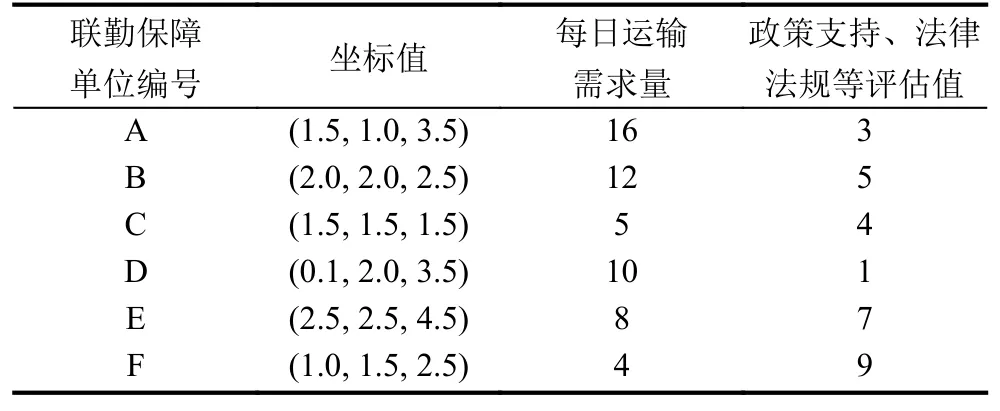
表1 装备物资日运输需求量和政策支持量化表
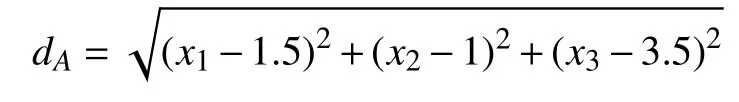
因联勤保障单位A的每天的运输需求是16吨,所以每天向A运输货物的费用是:
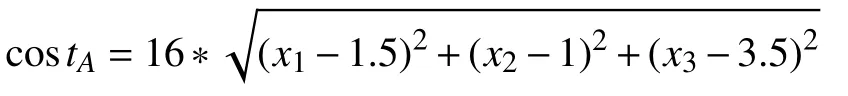
同理,可以得到物流中心向其他五个联勤保障单位运输货物每日所需的运输费用,由此得到费用最小化的目标函数如下:
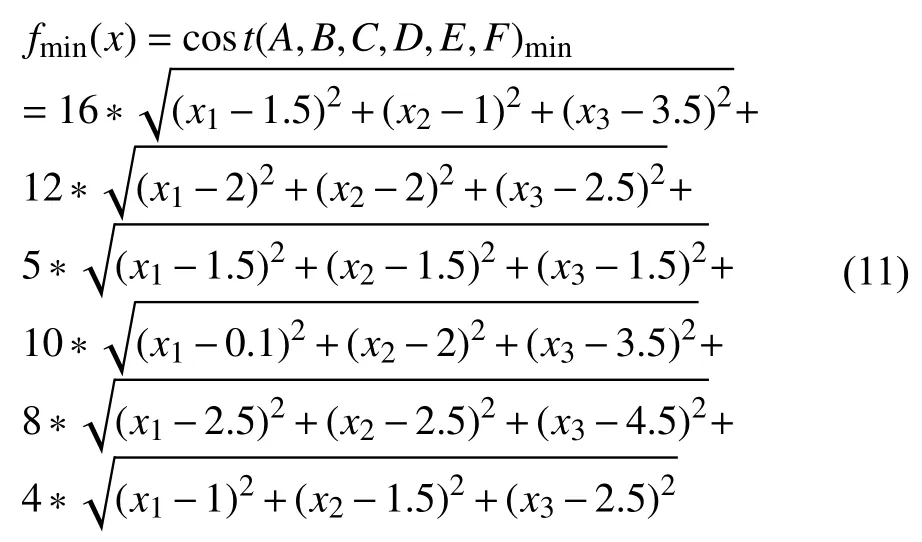
很显然,这个目标函数是非线性的,考虑到驻地运输能力和军工企业分布态势,经过相关领域专家和实地考察综合衡量评判,得出约束条件是:
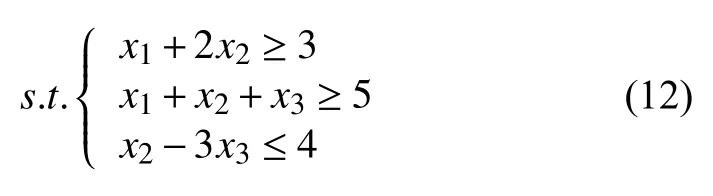
根据军事装备物流中心选址数学模型,按照模糊聚类遗传算法步骤进行优化求解,该算法的参数设置为: 种群规模为20,记忆库容量为10,迭代次数为100,交叉概率为0.5,变异概率为0.4. 运行结果如图3所示.可知,x1=1.38363;x2=0.54044;x3=0.22713,因此新选军事装备物流中心位置为P(1.38363,0.54044,0.22713),每日的最小运输费用为133.3317元. 加上政策支持、法律法规等评估值的权重系数,可计算得出具体选址位置.
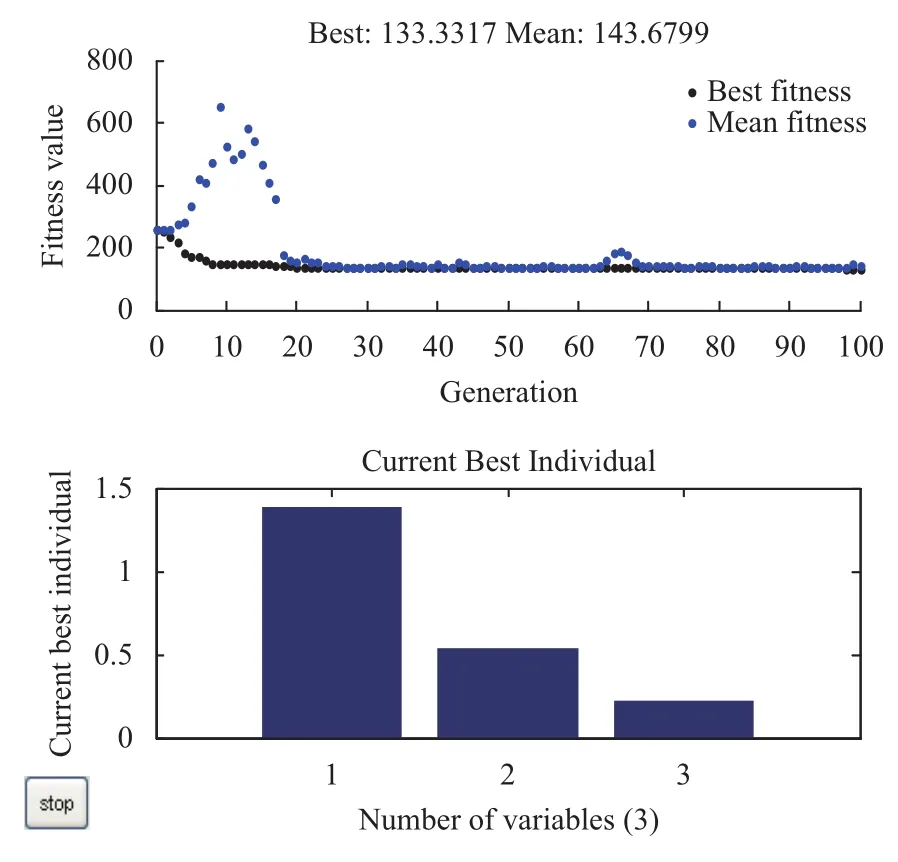
图3 模型优化结果
在实地调研的基础上,综合考虑当地政策、法律法规以及交通状况等,统筹兼顾、突出重点,是军事准备物流中心选址的基本准则. 在设计的算法模型中,经过多次运行实验,得到的军事装备物流中心选址结果趋于一致,可知该模型具有较好的鲁棒性; 对选址优化结果,采取实地分析测算和综合评估的方法,可知具体较高的可信度. 在本文中军事装备物流中心选址的问题主要考虑三维地理坐标和驻地兵工厂分布态势,但由于其他因素的不确定性,军事装备物流中心的选址还需要加强顶层设计和统一衡量.
5 结束语
兵马未动粮草先行. 军事物流中心是保障部队平时和战时履行使命任务的核心关键. 本文主要是对军事装备物流中心的选址问题进行了研究,提出模糊聚类网络模型和遗传算法相结合的思想,分析了现在联勤保障单位的三维坐标系,通过实例验证了算法的收敛性和鲁棒性,该模糊聚类遗传算法的求解结果随着进化代数的增加而逐渐优化,并没有出现早熟收敛现象,这说明本文提出的该算法求解结果具有较强的精确性和可信度,为解决较复杂的或规模较大的选址问题提供了新思路,也为决策者科学正确的选址问题提供重要参考.
1周志华,陈世福. 神经网络集成. 计算机学报,2002,25(1):1–8.
2施彦. 物流中心选址的神经网络集成模型研究. 计算机工程与应用,2009,45(16): 211–214. [doi: 10.3778/j.issn.1002-8331.2009.16.062]
3蔡良伟,李霞. 遗传算法交叉操作的改进. 系统工程与电子技术,2006,28(6): 925–928.
4潘伟,刁华宗,井元伟. 一种改进的实数自适应遗传算法. 控制与决策,2006,21(7): 792–795,800.
5卫绍元,王冬梅. 基于混合遗传算法的车辆路径问题. 交通运输系统工程与信息,2006,6(6): 49–52.
6廉晚祥,朱参世,胡江华,等. 改进遗传算法在应急救援物资运输中的应用. 中国安全科学学报,2013,23(5): 172–176.
7吴勇刚,徐香新,刘梅,等. 基于遗传算法的最优城市垃圾收运路线探究. 计算机仿真,2012,29(4): 259–262,312.
8孙全颖,王艺霖,杜须韦. 遗传算法在机械优化设计中的应用研究. 哈尔滨理工大学学报,2015,20(4): 46–50.
9包子阳,余继周. 智能优化算法及其MATLAB实例. 北京:电子工业出版社,2016: 13–16.
Application of Fuzzy Clustering Genetic Algorithm to Military Equipment Logistics Center Location
LV Xue-Yi1,ZHENG Shao-Yu2
1(Company of Postgraduate Management,Equipment of Academy,Beijing 101416,China)
2(Department of Equipment Acquisition,Equipment of Academy,Beijing 101416,China)
This paper analyzes the military equipment logistics center location problem and based on the analysis,builds the hybrid algorithm model which combines fuzzy clustering and genetic algorithm. The core technology is to integrate the fuzzy clustering network model into genetic algorithm in the process of building groups,which can effectively avoid the possibility for genetic algorithm to be prone to premature. The algorithm has been validated to be robust and reliable.The simulation results offer certain references for policy-makers to select the location more scientifically.
fuzzy clustering; genetic algorithm; location
吕学义,郑绍钰.模糊聚类遗传算法在军事装备物流中心选址中的应用.计算机系统应用,2017,26(12):170–174. http://www.c-sa.org.cn/1003-3254/6119.html
2017-03-16; 修改时间: 2017-04-05; 采用时间: 2017-04-17
