基于时刻表的多模式交通网络路径规划①

周佳丽,邓跃进

(武汉大学 测绘遥感信息工程国家重点实验室,武汉 430079)

基于时刻表的多模式交通网络路径规划①

周佳丽,邓跃进

(武汉大学 测绘遥感信息工程国家重点实验室,武汉 430079)

城市交通系统正逐渐由原来的单一模式转变为相互连通的多模式,为了更准确地表达多模式交通网络系统,并满足个人出行时路线规划和时间预测的要求,该文以Oracle空间网络数据模型为建模基础,以武汉市为例,选取了道路网、公交路网和地铁路网三种路网模式构建了多模式交通路网,并且加入公交线路和地铁线路的时刻表因素,旨在使出行者通过该模型可以找到到达目的地的最快路线并预估该路线所需时间.

多模式交通网络; 路径规划; Oracle 空间网络数据模型; 时刻表; 最短路径

随着经济的飞速发展,有限的生存空间和多样化的城市生活使人们的出行方式由单一模式逐步转向了多模式[1],交通基础设施建设也在不断地建立和完善中. 多模式交通是指出行者从对交通出行的便捷性和其自身出行的经济性考虑,选择多种混合的交通模式出行,常用的模式有步行,公交,地铁,出租车等. 如先步行到公交站点,乘公交到某一中转站再步行到地铁站换乘为地铁,最后在地铁站点下车步行至目的地.

本文以湖北省武汉市为例,建立了基于道路网、公交路网和地铁线路网的多模式交通网络模型,并添加了武汉市公交车时刻表和地铁时刻表数据来进行基于时刻表的多模式交通路网最短路径规划,给出行者提供了更为准确的到达时间预估.

1 多模式交通路网

路径规划一直以来是一个受到普遍学者研究的话题,从 Dijkstra 算法,Floyd 算法,A*算法,到后来从生物学领域获得灵感衍生出来的蚁群算法,其目标都是求取最短路径(或最少权重的路线)来到达目的地. 但是如Dijkstra和Floyd等算法都是在单一出行的交通网络上求解最短路径,没有对交通层次进行细分,忽略了交通出行方式多样性的现状[2]. 在实际生活中,如果只考虑了单层网络和单一模式交通出行方式,将难以适应城市交通出行从单一模式向一个多模式交通体系的转变,同时,更有效的路线规划算法还应该考虑其他因素,除了用户在交通工具上消耗的时间,还应考虑到从一个模式到另一个模式的换乘时间、用户在换乘时的等待时间等.

考虑了车辆行驶和到达的时间、等待时间和换乘所需的步行时间的多模式交通路网模型,更有利于规划最佳路线并准确预估到达时间. 很多学者都使用许多建模方法和算法来解决多模式交通路径规划的问题.李学全[3]基于随机用户平衡理论构造了多模式的交通配流模型; 熊丽音[4]采用了非平面数据模型,借鉴了ISO GDF 4.0 逻辑数据模型,建立了多模式交通网络及其连通关系的数据模型; 四兵锋[5]基于图论提出了一种分层网络结构来描述多模式交通系统,研究了出行者在该系统中的选择行为,并考虑了不同模式道路流量之间的相互影响; 李想[6]引入了超网络概念对多模式城市交通网络进行网络描述,利用基于图的遍历算法进行有效路径搜索,根据各交通模式自身的特点建立路段阻抗函数,最后用非集计方式描述出行者的弹性需求. 这些学者基于不同出发点建立了多模式交通系统并进行优化,但是很少考虑时间消耗问题. 刘新华[7]建立了基于乘客属性的地铁配流模型及算法,并考虑地铁需求的动态属性,建立基于时刻表的地铁客流动态分配模型及算法;刘志谦[8]在传统的Logit模型中引入公交路径独立系统,建立了容量限制下基于时刻表的随机用户均衡模型. 但是这些学者仅考虑了单一的出行模式,未考虑到多模式交通网络.

本文利用Oracle公司提供的网络数据模型[9](Network data model,NDM),可以较容易地构建多模式交通网络,并以湖北省武汉市为例,建立了基于道路网、公交路网和地铁线路网(仅考虑已投入运行的1号线、2号线和4号线)的多模式交通网络模型,添加了武汉市公交车时刻表和地铁时刻表数据来进行基于时刻表的多模式交通路网最短路径规划,给出行者提供了更为准确的到达时间预估.

2 构建多模式交通路网模型

Oracle空间网络数据模型是由Oracle公司设计开发的可用于分析网络连接关系的模型. 它将模型简化为4个主要的关系表: NODE站点表、LINK连接表、PATH路线表和PATH-LINK表,实体-关系图如图1所示. Oracle Spatial也提供了基于Java与路径分析相关的API以供开发者使用. 路网数据的查询和修改不仅可以在数据库中进行操作,还能在NDM编辑器(Network data model editor)中进行可视化查询和修改,有利于用户在此基础上进行二次开发.

图1 Oracle 空间网络数据模型实体-关系图

表1以NODE_ID为主键,用NODE_NAME存储的每一个公交汽车站和地铁站的名称; 由NODE_TYPE区分该点是公交站(BusStop)还是地铁站(Subway Stop); ACTIVE是便于在该站点的维修或取消之时方便更改或不参与计算; GEOMETRY存储每一个站点的几何信息; SDO_GEOMETRY 是 Oracle Spatial软件独有的数据类型表达,主要存储站点的坐标信息.

表1 站点表

表2以LINK_ID为主键,使用START_NODE_ID和END_NODE_ID来确定这条连接的方向,LINK_TYPE来区分连接的类型是地铁线路上的连接(Subway Link)、公交线上的连接(BusLink)、或是换乘的步行连接(TransferLink). 本模型选用的连接的成本cost是指行驶时间或换乘时间,单位是秒,一般是用该连接的实际距离除以交通工具或步行的速度. 根据一些参考文献和实际数据采集,本文定义了地铁速度为每小时60公里,公交车的速度为每小时30公里,换乘的速度相当于步行速度,平均每秒1.2米,以此计算出所有连接的时间成本.

表3以PATH_ID为主键,并使用PATH_NAME来记录每一条公交或地铁线路名称,如593路或地铁1号线等,START_NODE_ID和END_NODE_ID确定该线路是上行或下行方向,与NODE_ID关联,PATH_TYPE来区分线路的类型是公交线路(BusPath)还是地铁线路(SubwayPath),SIMPLE是用于判断该线路是否是简单线路.

表2 连接表

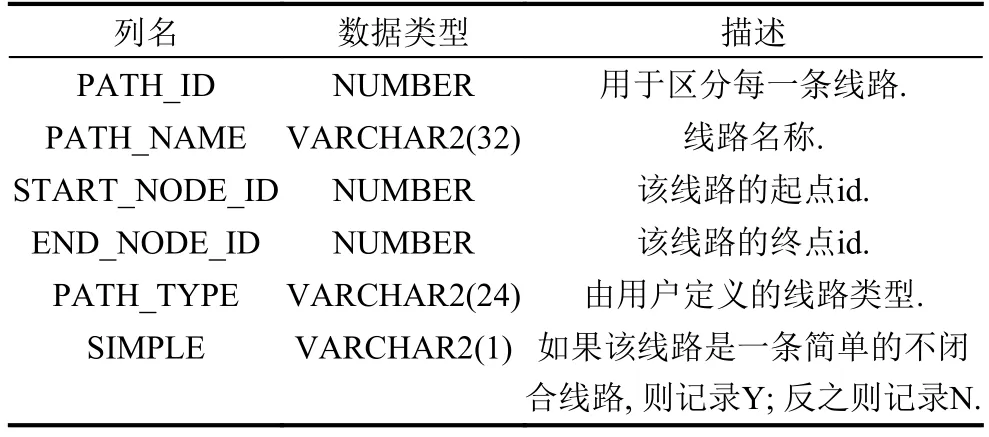
表3 线路表

表4是描述线路表和连接表关系的一个表格,以PATH_ID、LINK_ID和SEQ_NO为组合主键,LINK_ID和PATH_ID为表2和表3的主键,SEQ_NO代表该连接在该线路中的序列号.

表4 线路-连接表

3 基于时刻表的多模式交通路网模型

3.1 多模式交通路网规划

在第二章的建模中,本文规定了以时间作为成本的计算标准(见表2),而且各个交通模式的站点、连接、线路数据等均存储在同一站点、连接和线路表中,因此所求的最短路径即找出使用最少的时间到达目的地的路径,未考虑时刻表时的多模式交通网络路径的规划主要是采用Dijkstra算法. 该算法的基本思想是以起始点为中心,然后向外对路径成本层层迭代,从而得到从起点到其他节点的最短路径. 具体表现为: 首先确定起始站点s和终点站点t; 把所有站点分为S组和V组,S组代表已求出的最短路径的站点集合,V组为尚未确定的站点集合,初始的S组只有起始站点s; 从V组中选取一个距离s最小的一个站点i,将i从V组移到S组; 以i为新考虑的中间点,则站点s→站点i→V组中各个站点的距离将缩短,修改这些距离值,选取当前状态下距离值最短的站点j移入S组中; 将站点j作为第二个中间点,寻找站点s→站点i→站点j→V组中各个站点的最短距离,重复上述步骤,直到从V组移入S组的站点为终点站点t为止,该条路径即为从s站点到t站点的最短路径.

综上,此条件下的多模式交通路网模型规划的主要实现流程如下:

(1)设置起始站点s和终点站点t.

(2)采用宽度优先搜索算法,快速判断起始站点s和终点站点t是否在路网中连通. 如果判断结果为连通,则进行下一步开始计算最短路径,反之说明两点之间不存在连通关系,退出计算过程.

(3)用上述提及Dijkstra算法,算出从s到t的最短路径. 值得一提的是,Oracle Spatial提供了 Dijkstra 算法的Java API以供开发者使用.

(4)对得到的最短路径进行处理,输出结果. 根据模型的设计将所得的最短路径转化为指导用户换乘的、具有可读性的规划信息,还可以预估到达目的地的所需时间.

3.2 基于时刻表的多模式交通路网规划

在实际日常生活中,并不是每次到达站点时公交车或地铁都会正好出发,更多时候出行者都需要在原地等待交通工具的到来. 而且某一条线路表面上看虽然空间距离较短,但是由于该线路的发车间隔时间较长,导致用户需要等待的时间更多,反而可能会比一条空间距离长但等待时间短的线路更晚到达目的地. 完整的出行时间的计算,应该是等待时间、交通工具的行驶时间和换乘时间的总和. 添加了时刻表这一参考因素将等待时间纳入模型中,更有利于出行者能够准确预测到达目的地的时间,即基于绝对时间[10]的多模式交通网络路径模型.

绝对时间需要时刻表数据进行支持,数据的存储结构详见表5. 该表以 PATH_ID,RUN_ID 和 NODE_ID为组合主键. PATH_ID和NODE_ID即为表3和表1中的主键,RUN_ID是指不同班次的公交车和地铁,ARRIVAL_TIME和DEPARTURE_TIME代表该路线到达和离开该站点的时间. ACTIVE字段是用于描述此次班次是否可用,当交通工具没有准时到来时,用户可以暂时将此字段改变为0,不参与新的路径规划的计算当中,退出程序时再更新回1即可.

表5 时刻表

模型引入了三维时空坐标系来描述交通工具的行驶规律,如图2所示,X轴和Y轴构成一个平面用于表达位置坐标,点A到F分别代表不同位置的公交站点或地铁站点; 竖轴为时间坐标,图中截取了从12:00到12:40的时间段; 每条线路代表不同的班次,线路1a和线路1b表示同一趟线路的两个不同班次,线路1a由12:00发车从A站点发车,12:15到达D站点,线路1b比线路1a晚10分钟,线路2于12:20从E站点发车,途径B、C 站点,于12:40到达F 站点.

图2 三维时空坐标系下的交通路网模型[11]

假设某人想从站点A到站点F,于11:55分到达了站点A,他需要在A站点等待5分钟,乘坐线路1a于12:10分到达站点C下车,在C点等候20分钟换乘线路2,于12:40到达F点. 因此总的出行时间共为45分钟,包含了5分钟的等待时间、20分钟的行驶时间和20分钟的换乘时间.

4 实验与结果

将武汉市交通数据导入到Oracle空间网络数据模型后,模型中共包含武汉市7152个站点,其中包括7074个公交车站和78个地铁站(仅考虑武汉市内已运营的地铁1号线、2号线和 4号线); 共包含14432条有向连接,包括13596条公交连接、150条地铁连接和686条换乘连接(其中规定只有当两个不在同一条路线上的站点之间距离小于150米时才允许创建换乘连接); 共包含 558条有向行驶线路,包括552条有向公交线路和6条有向地铁线路. 所构建的武汉市多模式交通系统如图3所示.

图3 武汉市交通路网

由于公交车路线和地铁路线的时刻表数据量较为庞大,故本文只选取了部分数据进行实验. 路径规划算法由Java语言实现,需要用户输入起始站点名称和终点站点名称,数据库将模糊查询出与之相对应的站点ID,当用户再输入出发的时间后,程序便可输出最优路线以及该路线到达的时间. 流程图见图4.

以“广埠屯站-鲁磨路地质大学站”和“磨山景区-积玉桥”两条线路为例,见表6,未加入时刻表因素前,模型由Dijkstra算法可以得出最短路径所消耗的时间成本分别为737秒和1932秒,到达时间仅仅是简单地将时间成本由秒数转化分钟. 加入时刻表后,消耗的时间成本不变,但是到达时间和未加入时刻表之前相比均有延后,这是考虑到用户在原地等候和公交车上车下车、地铁的站点停靠等所花的时间成本. 而且不同的出行时间也可能会影响到路线的选择,第一条线路中所示12:19出发和12:21出发,虽然出发的时间仅隔了两分钟,但是得出的出行路线完全不同,甚至12:21出发时,74 路虽然 cost更高,但是到达的时间更早; 第二条线路中,不同的出发时间虽然没有导致路线的选择发生改变,但是预估的总消耗时间均有变化. 因此,将交通工具的时刻表作为多模式交通网络路径规划的一个参考因素是非常有必要的. 该模型路径规划的计算过程在Windows7 64位操作系统下3.00 GHz处理器的环境中完成,数据库使用的是 Oracle 12c,运行速度良好,实现了基于时刻表的多模式交通路网规划.

5 结论与展望

以武汉市为例,在Oracle空间网络数据模型上进行多模式交通路网的建模是可行且易于实现的,加入了时刻表因素后的路线规划可以根据不同的出行时间选择不同的路线,更准确地预估到达时间.

但是该研究也存在一些不足,由于国内时常会有交通堵塞的情况,且拥堵情况也是随着时间进行波动的,因此公交车的到达时间和离开时间并不能很好地遵守时刻表. 本模型虽能够使用户在车辆未准时到达时主观地将该趟班次不参与新的路径规划的计算中,但若该班次只是短暂延误,新计算出来的规划路线可能仍不是最优选择. 后续考虑能将本模型与实时交通状况、公交车GPS定位技术相结合,在定位公交车地点后,根据实时路况或历史路况记录,计算出延误时间,更新时刻表中的数据,以达到真正的准确预计和规划.

图4 基于时刻表的最短路径规划流程图

表6 时刻表对的路径规划的影响

1吴信才,杨林,周顺平,等. 支持多模式的复合交通网络模型研究. 武汉大学学报·信息科学版,2008,33(4): 341–346.

2仇宁海,秦勇. 基于多层-多模式交通网络的最短路径分析的研究. 2007第三届中国智能交通年会论文集. 北京.2007.

3李学全,刘美娇. 多模式城市交通网络随机用户平衡配流模型. 数学理论与应用,2007,27(2): 101–104.

4熊丽音,陆锋,陈传彬. 城市多模式交通网络特征连通关系表达模型. 武汉大学学报·信息科学版,2008,33(4): 393–396.

5四兵锋,杨小宝,高亮,等. 基于出行需求的城市多模式交通配流模型. 中国公路学报,2010,23(6): 85–91.

6李想. 考虑换乘的多模式城市交通网络配流问题研究[硕士学位论文]. 成都: 西南交通大学,2015.

7刘新华. 基于时刻表的地铁动态配流模型研究[博士学位论文]. 西安: 长安大学,2013.

8刘志谦,宋瑞. 基于时刻表的公交配流算法研究. 重庆交通大学学报 (自然科学版),2010,29(1): 114–120.

9Spatial O. Oracle Spatial Quadtree Indexing,10g Release,1(10.1). 10g White Paper,2006.

10闻辉,刘岳峰,郑江华,等. 基于时间链的公交网络数据模型研究. 地理与地理信息科学,2005,21(3): 35–38.

11Thorlacius P. Time-and-space modelling of public transport systems using GIS. Transportrådet og Aalborg Universitet,1998.

Multi-Mode Traffic Network Path Planning Based on Schedule

ZHOU Jia-Li,DENG Yue-Jin

(State Key Laboratory of Information Engineering in Surveying,Mapping and Remote Sensing,Wuhan University,Wuhan 430079,China)

The urban traffic system is gradually changing from a single mode to interconnected multi-mode. In order to express the multi-mode traffic network system more accurately and meet the requirements of personal route planning and time prediction,this paper selects Oracle spatial network data model as the modeling foundation. The model takes Wuhan City as an example,and selects the road network,bus network and railway network to construct a multi-mode traffic network. Also the schedule of bus lines and subway lines is added to allow the travelers to find the quickest path to destination and to estimate the time required for the route.

multi-mode traffic network; path planning; Oracle spatial network data model; schedule; shortest path

周佳丽,邓跃进.基于时刻表的多模式交通网络路径规划.计算机系统应用,2017,26(12):160–164. http://www.c-s-a.org.cn/1003-3254/6075.html

国家重点研发课题(2016YFB0502201)

2017-03-06; 修改时间: 2017-03-23; 采用时间: 2017-03-27