文化与思想并重，探究与应用共存

吴佳薇

[摘  要] 理解勾股定理、灵活使用勾股定理解决实际问题是“勾股定理”学习的基本要求，另外在教学中需要注意对数学文化的传播，让学生感受定理的文化内涵，同时需要渗透数学的思想方法，发展学生的数学思维. 本文将从文化传播、探究活动、思想渗透和定理应用四个方面展开教学探讨，与读者交流学习.

[关键词] 勾股定理;文化;探究;思想方法;应用

“勾股定理”是人教版数学教材八年级下册的重要内容，该定理是人们通过图形拼接得到的，用于研究直角三角形的三边关系，在几何中有着非常重要的作用. 根据课标要求，对于勾股定理的教学，不仅需要引导学生理解定理、学习使用定理解决问题，还需要渗透思想方法，让学生充分感受勾股定理的文化价值.

注重背景介绍，传播数学文化

勾股定理的发现与应用有着悠久的历史，教学中应注意展示与勾股定理有关的历史故事，使学生对勾股定理的发展历程有初步的了解，从而深刻感受勾股定理本身所蕴含的文化内涵，这对激发学生的学习兴趣极为有利.

我国对勾股定理的研究有着诸多贡献，教学中可以重点介绍我国古代的一些研究成果，例如结合教材引言向学生介绍《周髀算经》中记载的“如果勾是三、股是四，那么弦是五”，使学生了解我国古代对勾股定理的研究历史. 而在勾股定理的证明阶段，可以重点介绍我国古人赵爽的弦图证明思路. “赵爽弦图”是古人智慧的充分展现，对弦图的学习可以较为简洁地实现定理的证明，加深学生的民族自豪感. 对于课堂练习的选题，可以参考数学著作《九章算术》，充分展现古人在勾股定理应用方面的研究成果. 同样，也可以介绍国外的研究成果，如讲解勾股定理的发现过程可以引入毕达哥拉斯的故事，而对逆定理的讲解可以引入希腊哲學家柏拉图关于勾股数的结论. 课后学习环节可以安排大家收集勾股定理的其他证明方法，通过交流、探讨的方式来加深学生对定理的理解.

勾股定理的背景知识讲解，能让学生了解我国古人对勾股定理研究的贡献，能有效地激发学生的爱国情怀，能培养学生的民族自豪感，同时，合理利用背景材料，能激励学生奋发学习.

创设多样活动，亲历探究过程

勾股定理作为中学数学最为重要的定理之一，有着广泛的应用. 该部分内容不仅需要学生学习使用勾股定理来解决和证明问题，还需要学生通过教学内容的学习具备探究性学习和总结知识的能力. 因此，开展探究式教学，让学生亲历勾股定理的探究过程显得尤为重要.

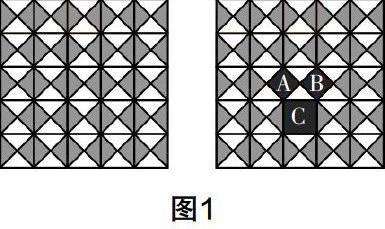
探索勾股定理，可以从特殊三角形入手. 例如，给出铺地板的方案，如图1，让学生思考图中正方形A，B，C面积之间的关系，引导学生发现等腰直角三角形的性质：以等腰三角形两条直角边为边长的小正方形A和B的面积之和等于以其斜边为边长的大正方形C的面积.

接着，让学生思考：是否任意直角三角形都存在这样的三边关系. 教师可以设置画图活动，让学生在方格纸上画一个三个顶点均在格点上的任意直角三角形，然后分别以该三角形的各边为边长向外作正方形. 通过对比、观察，如图2，学生会发现同样符合上述性质，进而得出一般性的猜想.

最后，需要教师引导学生对其进行验证，即通过剪切、拼接的方式，引导学生将两个面积分别为a2和b2的正方形拼成一个面积为c2的正方形. 需要注意的是拼接方法不唯一，此时需要教师引导学生尽可能地探究不同方案，扩展学生思维的开阔性，如图3. 在探究的最后阶段需要将验证的结论上升到理论高度，即假设直角三角形的直角边长分别为a，b，斜边长为c，则三边关系为a²+b²=c².

从瓷砖铺地、格子绘图再到拼图验证，学生充分经历了“观察—猜想—归纳—验证—总结”的探究过程，在这个过程中，学生充分参与，用自己的创造和体验来学习新知，从而深刻地掌握了数学定理. 具有探究性的实验课堂，对学生创新精神和实践能力的提升有极大的促进作用.

渗透思想方法，发展数学思维

义务教育强调教学的核心不是知识，而是数学的思维方式，应注重思想方法的教学. 对于勾股定理的教学，也不应止于知识本身，还需要在教学中渗透数学思想方法，重视学习方法的指导，尤其是勾股定理的发现和验证过程需要渗透从特殊到一般的思想、数形结合思想，以及转化思想.

勾股定理的发现过程蕴含了从特殊到一般的思想，例如教学中引入了古希腊数学家毕达哥拉斯到朋友家做客时发现朋友家用地砖铺成的地面反映出的直角三角形的特性. 首先研究等腰直角三角形的三边特性，紧接着从特殊到一般，让学生猜想任意直角三角形的三边关系，从而得出具有普遍适用性的勾股定理. 在该过程中，教师需要向学生传达从特殊到一般的数学思想，即从特殊现象中发现一般规律，并确定其适用性.

而在验证勾股定理的过程中，需要结合转化思想和数形结合思想，如把握勾股定理中边长平方的特点，建立边长与面积的关系，将探究直角三角形的三边关系转化为探求正方形的面积关系. 验证过程中需要引导学生首先从“形”的角度来观察，即直角三角形的三条边均为各正方形的边，如图4.

勾股定理的发现，使得数学从较为单一的数字运算上升到了结合几何图形进行论证的高度. 无论是拼图过程还是数字证明，都充分渗透了转化思想和数形结合思想，其对提升学生思维的活跃性有着积极的作用. 结合从特殊到一般的思想方法，其对学生分析问题和解决问题能力的提升也有极大的帮助.

结合实际问题，注重定理运用

勾股定理作为直角三角形的重要定理，其本身就具有极大的应用价值，因此将定理学习上升到实用高度就显得尤为重要. 教学中需要指导学生应用勾股定理来解释生活中的问题，帮助学生掌握从实际问题中抽象解决问题的几何模型，从而有效地加深学生对定理的理解.

例如，教学中可以引入木板进门问题：有一门框的尺寸如图6，长1 m、高2 m，一块长为3 m、宽为2.2 m的木板是否可以从门框中通过？请说明理由.

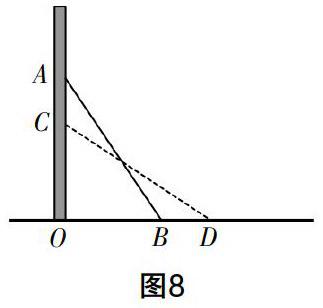
教学中也可以引入动态问题，以梯子滑动问题为例：如图8，梯子AB长3 m，斜靠在竖直的墙AO上，此时AO的距离为2.5 m.（1）请大家思考梯子底端B距墙角O的长度;（2）如果梯子的顶端A沿着墙体下滑0.5 m至点C，底端B滑动的距离是否也是0.5 m？该问题来自生活现象，训练时需要教师指导学生利用准确的语言来表达数学过程，即把实际问题转化为数学问题，并建立相应的几何模型，利用几何模型的直观、简洁性，结合勾股定理来解释生活问题. 值得注意的是，由于实际问题中存在滑动前和滑动后两个状态，所以需要教师引导学生建立两个几何模型，如图9，然后利用模型分别求解问题.

勾股定理与生活问题的紧密结合，可以有效培养学生的应用意识，让学生充分感受数学定理之美. 另外，从实际问题中抽象出几何模型，利用定理来解决问题，可以使学生充分认识到数学学习的本质：源于生活，服务于生活.

总之，勾股定理作为平面几何度量的基本定理，无论是知识层面，还是思想情感层面，都承载着众多的教学价值. 对于勾股定理的教学，教师要注重背景材料的讲解，要向学生传达定理背后蕴含的数学文化，以激发学生的学习兴趣;教学中应创设多样的活动，让学生亲历探究过程，培养学生的创新精神和实践能力，渗透思想方法，提升学生的数学思维能力;应结合实例应用定理，培养学生的应用意识，让学生感受定理的应用之美.