不同放养规格和放养密度下吉富罗非鱼体长生长模型研究
2018-01-06陈倩苏胜彦刘思辰叶伟朱伟凡袁新华
陈倩+苏胜彦+刘思辰+叶伟+朱伟凡+袁新华


摘要: 为研究不同放养规格和养殖密度下吉富罗非鱼的体长生长规律,采用von Bertalanffy、Gompertz、Logistic、Brody 4种生长模型对吉富罗非鱼体长的生长进行拟合,使用R-Studio软件自行编程求出模型中各生长参数,以AIC统计量作为确定吉富罗非鱼体长最优生长模型的准则。结果表明,4种模型均能很好地模拟吉富罗非鱼生长曲线,其中平均体长为0.8 cm (SL1)的试验组以Gompertz模型为最佳,平均体长为(2.8±0.14)cm (SL2)的试验组以Logistic模型为最佳。体长生长瞬时生长速度曲线均呈先上升再下降的趋势,SL2试验组比SL1试验组更具养殖优势,养殖密度为15尾/m2(D1)的个体生长状况优于养殖密度为30尾/m2(D2)和60尾/m2(D3)的个体生长状况。研究结果可为吉富罗非鱼的育种研究、规模化养殖及养殖管理模式优化提供理论依据。
关键词: 吉富品系尼罗罗非鱼;生长模型;AIC准则;体长;规格;密度
中图分类号: S965.125 文献标志码: A
文章編号:1002-1302(2017)22-0170-06
罗非鱼(Tilapia)属慈鲷科非鲫属,外形类似鲫鱼,鳍条多刺,原产于非洲的坦噶尼喀湖,俗称非洲鲫鱼、非洲仔等。联合国粮农组织(FAO)在1976年向世界推广养殖罗非鱼,其作为物美价廉的经济鱼类,快速获得世界各国的认可与养殖,也是中国主要的养殖鱼类之一。吉富罗非鱼具有生长速度快、养殖周期短、食性杂、抗病力强等优点,在广东省、海南省、福建省、云南省和广西壮族自治区这5个主产区实现了大规模养殖。范立民等在研究养殖密度对吉富罗非鱼的生长性状的影响时发现,放养密度为27 000尾/hm2时,吉富罗非鱼的体长和体质量要小于放养密度为18 000尾/hm2和22 500尾/hm2时,高密度会对罗非鱼的生长产生负影响[1]。朱佳杰等研究发现,吉富罗非鱼放养规格为2.5~2.7 cm的试验组比0.8~1.0 cm 和1.2~1.5 cm的试验组的亩产量、成鱼规格、成活率高[2]。因此,研究不同放养规格和养殖密度下吉富罗非鱼的生长情况,以量化模型研究其生长发育规律,对吉富罗非鱼的养殖发展具有重要意义。
生长模型可以反映生物个体生长发育的规律性变化[3-4],鱼类的生长曲线研究有助于掌握鱼类的生长规律[5]。国内对吉富罗非鱼的生长模型研究仅限于同种规格和密度的研究,如唐章生等用4种生长模型对网箱单养吉富罗非鱼的生长进行了拟合,得出VB-GF生长模型对体质量生长的拟合效果最好,而Gompertz GF生长模型对吉富罗非鱼体长生长的拟合效果最好[6];肖俊等对尼罗罗非鱼生长相关参数进行生长模型构建,对尼罗罗非鱼的生长发育规律进行了研究,得出Logistic、Gompertz、Bertalanffy这3种模型均能很好地模拟尼罗罗非鱼生长曲线,其中以Logistic模型的拟合度最高[7]。而对于罗非鱼在不同密度和放养规格的情况下的生长模型研究尚未见报道。本研究采用4种常用的生长模型拟合吉富罗非鱼在2种放养规格和3种放养密度下的生长,揭示其体长生长规律,旨在为吉富罗非鱼育种研究、养殖模式选择和养殖生产经济性状预测提供理论依据。
1 材料与方法
1.1 试验材料
1.1.1 试验用鱼 供试吉富罗非鱼由中国水产科学研究院淡水渔业研究中心屺亭科研实验基地提供。设置2种放养规格,每种分别为4 200尾,试验鱼体长均值为0.8、(2.8±014)cm,用SL1、SL2表示。
1.1.2 试验池塘 试验地点设于中国水产科学研究院淡水渔业研究中心屺亭科研实验基地,试验池塘为12个长方形水泥池 (长×宽×高为10.0 m×2.0 m×1.5 m)。养殖用水为 地下水,水质清新,养殖水深1.0 m,水温变化范围为24~33 ℃。微孔增氧,昼夜增氧,以保证氧气充足。每日清除池塘内残饵和粪便,视情况进行换水处理,每次换1/3水。
1.2 试验方法
1.2.1 密度设置 SL1和SL2均设置15尾/m2(D1)、30尾/m2(D2)、60尾/m2(D3)3种不同放养密度,每种放养密度设置2个水泥池作为对照。
1.2.2 饲喂 试验选用浙江宁波天邦股份有限公司生产的罗非鱼粉料和膨化配合饲料(其中有0号罗非鱼料、1号罗非鱼料和2号罗非鱼料)。前期投喂加水混好的罗非鱼粉料,根据鱼体的不同生长阶段依次投喂0号罗非鱼料、1号罗非鱼料以及1号罗非鱼料和2号罗非鱼料的混合料。试验时间为2016年7月4日至2016年10月26日。采取饱食喂法,每日投饲量根据水温和鱼群吃食等具体情况调整。
1.2.3 数据测量 每周测量鱼的体质量、体长各1次,使用精确度为0.001 g的电子天平测定鱼体质量,使用精确度为0.02 mm的游标卡尺进行体长测量。每次从每个试验池中分别随机取30尾进行测量,测完放回,共进行15次测量。
1.3 数据分析
1.3.1 模型选择 本研究选取4种常用的生长模型来模拟吉富罗非鱼体长的生长,各模型和拟合度见表1。
1.3.2 模型选择准则 本研究采用统计模型选择中广泛应用的赤池信息量准则(Akaikes information criteria,常简称AIC)作为选择最佳模型的准则[9-10]。
1.3.3 生长参数估计方法 使用R-Studio软件自行编程求解方程,用Excel 2007软件作折线图。
2 结果与分析
2.1 不同规格和密度下体长生长曲线的分析
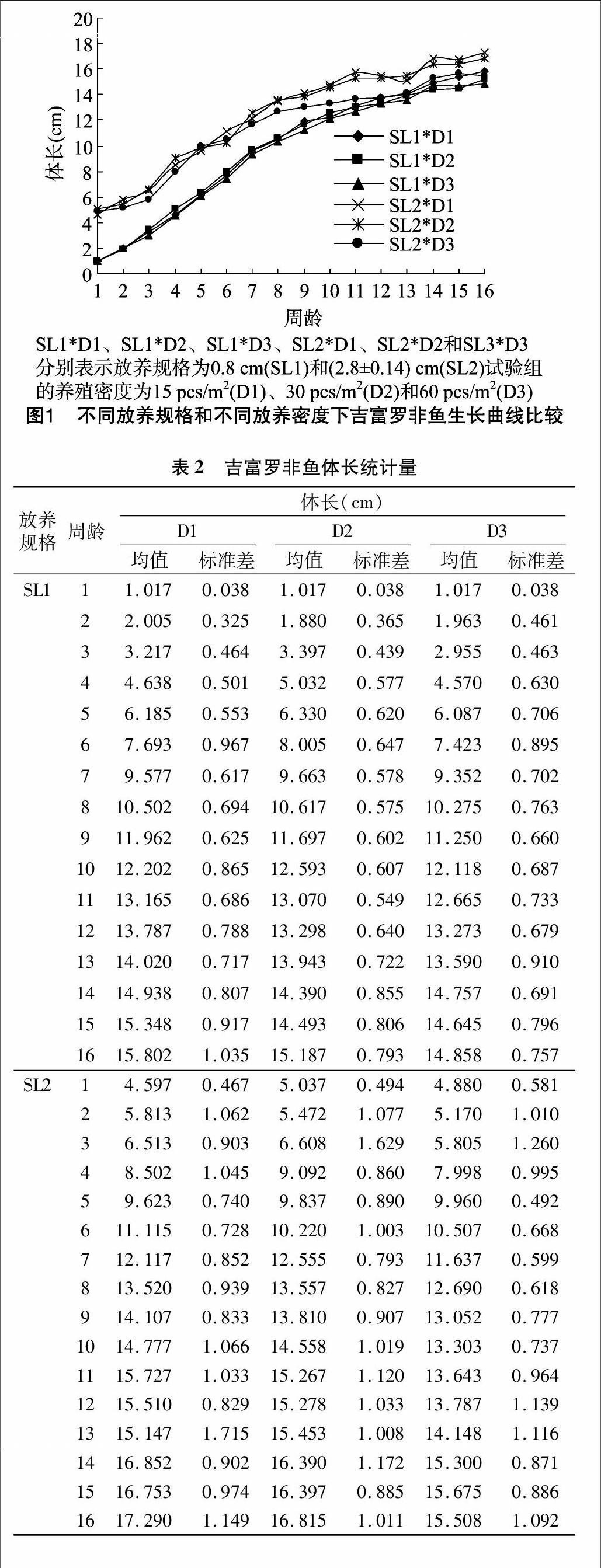
不同周龄吉富罗非鱼SL1和SL2试验组的体长在D1、D2、D3这3个密度梯度下均呈不断增长的趋势(图1)。SL1试验组养殖前期吉富罗非鱼体长增长趋势相同,从3周龄开始,D2的长势明显快于D3,但12周龄开始趋于相同,总体是D2快于D3。SL1试验组D1密度下的吉富罗非鱼的体长增长速度介于D2与D3之间,但最后3周明显快于D2和D3。SL1试验组3个养殖密度中,吉富罗非鱼的总体体长增长速度是D1>D2>D3。SL2试验组中,从2周龄开始,D3密度下吉富罗非鱼体长增长速度慢于D1和D2,从7周龄开始,明显落后于D1和D2。从9周龄开始,D1密度下的吉富罗非鱼体长增长速度快于D2密度下。SL2试验组中,吉富罗非鱼的总体体长增长速度是D1>D2>D3。该研究中,SL2试验组是SL1试验组经由约15 d养殖所得,后期吉富罗非鱼SL2试验组的体长增长速度较SL1试验组明显更快(图1、表2),表明SL2试验组比SL1试验组更具养殖优势。endprint
2.2 体长性状的模型拟合
由表3、表4可知,各模型的预测标准误为0.003~0407,R2均大于0.922,方差分析(ANOVA)结果显示各模型F值具有高度统计学意义(P<0.001),这表明各模型的拟合度都较好。
2.3 最优模型的确定
由AIC准则的统计值和R2可知,SL1试验组D1密度下von Bertalanffy模型和Gompertz模型的R2同为最大值 0.977,AIC值分别为 2 138.708 和2 142.999,相差甚微,但Gompertz模型拟合的体质量值与观察值更为符合,说明Gompertz模型拟合SL1试验组D1密度下的体长生长更合适。SL1试验组D2密度下Gompertz模型的AIC值最小,为 1 861.234,R2最大,为0.981,Gompertz模型拟合的体质量值与观察值比较符合,说明Gompertz模型拟合SL1试验组D2密度下的体长生长更合适;SL1试验组D3密度下Gompertz模型的AIC值最小,为 2 080.491,R2的值最大,为0.977,Gompertz模型拟合的体质量值与观察值比较符合,说明Gompertz模型拟合SL1试验组D3密度下的体长生长更合适(表3、图2)。SL2试验组D1密度下,Logistic模型的AIC值最小,为2 812.770,R2的值最大,为0.938,Logistic模型拟合的体质量值与观察值比较符合,所以Logistic模型拟合SL2试验组D1密度下的体长生长更合适;SL2试验组D2密度下Logistic模型的AIC值最小,为 2 869.084,R2的值最大,为0929,Logistic模型拟合的体质量值与观察值比较符合,所以Logistic模型拟合SL2试验组D2密度下的体长生长更合适;SL2试验组D3密度下Gompertz模型和Logistic模型的AIC值分别为2 736.674和 2 742.390,相差较微小,Gompertz模型和Logistic模型的R2的值分别为0.926和0.925,相差也较微小,但Logistic模型拟合的体质量值与观察值更为符合,所以Logistic模型拟合SL2试验组D3密度下的体长生长更合适(表4、图2)。
2.4 体长的绝对生长速度和生长拐点
为反映体长在其生长过程中某一时刻点的增长率,由模型的一阶导数求得体长关于时间的瞬时生长速度[8,11-13]。由图3可知,SL1试验组不同密度下的Gompertz模型和SL2试验组不同密度下的Logistic模型描述的吉富罗非鱼体长瞬时增长速度变化趋势大致相同,均为先上升后降低。SL1试验组不同密度下的Gompertz模型描述的曲线在4周龄同时达到峰值;SL2试验组不同密度下的Logistic模型描述的曲线变化趋势不完全一致,其中D1和D2密度下模型描述的曲线在4周龄同时到达峰值,D3密度下模型描述的曲线在3周龄达到峰值。
整个生长过程中生长速率最大值点即是生长曲线的拐点。由表5可知,SL1试验组不同密度下的Gompertz模型的拐点分别出现在4.862、4.476、4.776周,拐点体长分别为6017、5.648、5.731 cm,还比较相近。SL2试验组不同密度下Logistic模型的拐点分别出现在4.220、4.026、3.800周,拐点体长分别为8.608、8.442、7.718 cm。SL2试验组D3密度下的拐点出现时间相对较早,拐点性状值相对较小。
3 讨论
3.1 不同放养规格和密度下的体长生长特征
体长是影响吉富罗非鱼雄鱼的重要性状指标,并且相对体质量指标来说,体长指标可以最大限度地减少环境的影响[13],所以本试验采用体长指标讨论吉富罗非鱼的最优生长模型。范立民等发现体长指标在吉富罗非鱼养殖中对体质量的影响较大,尤其在低密度养殖中最显著,因此可以利用吉富罗非鱼的体长生长模型预测后期的体长和体质量,达到对体质量的早期选择[1]。
该研究中SL2试验组是SL1试验组经由约15 d养殖所得, 后期吉富罗非鱼SL2试验组的体长增长速度较SL1试验
组明显更快,且本试验结束时间为10月26日,此时气温开始下降,吉富罗非鱼需转移进温室进行保温养殖,若此时体长达到一定标准,第2年温度升高后,吉富罗非鱼的体质量较易增长,因此SL2试验组比SL1试验组更具养殖优势。吉富罗非鱼总体体长增长速度是D1>D2>D3。
鱼类在人工养殖过程中可能因为抢食不均而遭受饥饿胁迫[14-15],处于饥饿胁迫的鱼类在恢复食物供给后会出现一段快速生长期,其生长速度快于同期非饥饿的鱼类,这一现象称为鱼类的补偿生长[16-17]。SL1试验组D3密度下的Gompertz模型描述的吉富罗非鱼体长瞬时增长速度曲线后期高于D2密度下的曲线,可能是一种补偿生长现象。
3.2 最适生长模型的选择
一个完整的生物体生长过程可以用一条S形曲线表示,根据其生长速度的快慢,一般可以分为初始生长阶段、指数生长阶段和稳定生长阶段这3个阶段,且具有“慢-快-慢”这样的生长特征[8,11,18-22]。SL1和SL2试验组中,吉富罗非鱼體长生长曲线经过峰值后都是不断下降,趋近于零,符合鱼类生长的规律。虽然SL1和SL2试验组在生长过程中有一段生长是有重叠的,但我们发现不同规格适合不同的生长模型。
在动物生长最优模型的研究上,不同物种或同一物种的研究结果都不完全相同,可能受研究对象的生长环境和养殖模式影响[12,23-24],并且不同的生长发育阶段也可能会呈现不同的生长规律[25-27]。同一鱼类种苗不同,预测模型也可能不同[7]。Gompertz模型和Logistic模型在较多鱼类体长研究中适用,唐章生等发现Gompertz GF生长模型对网箱养殖吉富罗非鱼体长生长的拟合效果最好[6],何小燕等发现Logistic模型对大口黑鲈体长生长拟合效果最佳[24],郭媛等发现Gompertz生长模型对美洲红点鲑(A)和白斑红点鲑(B)及其杂交子代的体长生长曲线拟合效果最好[5]。Gompertz和Logistic模型不仅对吉富罗非鱼体长拟合度高,并且曲线描述的体长瞬时增长速度变化趋势和拐点时间也符合2种放养规格下的吉富罗非鱼的体长生长规律,所以该研究认为Gompertz和Logistic模型可分别作为SL1和SL2试验组下的最适体长生长模型。endprint
3.3 模型在吉富罗非鱼养殖中的指导意义
在实际养殖生产中,可以根据建立的吉富罗非鱼的生长模型对其生长情况进行预测,根据不同生长阶段的特点来确定吉富罗非鱼的养殖生长潜力,优化养殖管理模式,实现吉富罗非鱼养殖经济效益最大化[12]。本研究对不同放养规格和养殖密度下的吉富罗非鱼生长规律进行探索,其生长模型的建立将有助于为养殖户选择放养规格和养殖密度提供重要参考;此外,也可以为不同规模的养殖户在不同情况下选择最佳的养殖模式提供理论指导。
参考文献:
[1] 范立民,Kamira B,宋 超,等. 不同养殖密度下吉富罗非鱼生长性状的通径分析[J]. 中国农学通报,2015,31(11):83-87.
[2]朱佳杰,甘 西,谢尔登,等. 放养规格、养殖密度和水深对吉富罗非鱼养殖效果的影响[J]. 水产科技情报,2012,39(2):99-101.
[3]刘旭光,高 丽,赵益贤. 淮南麻黄鸡生长曲线分析与拟合的研究[J]. 安徽农业大学学报,1997,24(4):362-365.
[4]李乃宾,杜炳旺,杨芬霞,等. 贵妃母鸡生长模型拟合和分析的比较研究[J]. 家禽科学,2015(2):9-11.
[5]郭 媛,户 国,谷 伟,等. 美洲红点鲑和白斑红点鲑及其杂交子代幼鱼的生长曲线拟合[J]. 中国水产科学,2015,22(1):51-58.
[6]唐章生,林 勇,杨慧赞,等. 吉富罗非鱼生长模型研究[J]. 广东农业科学,2011(18):104-107.
[7]肖 俊,凌正宝,唐瞻杨,等. 尼罗罗非鱼(Oreochromis niloticus)生长相关分析及生长模型构建[J]. 海洋与湖沼,2012,43(6):1272-1278.
[8]符世伟,刘志刚,王 辉,等. 马氏珠母贝壳长生长模型研究[J]. 广东海洋大学学报,2008,28(4):30-35.
[9]王 辉,郭 宏. AIC准则应用于动物最佳生长模型的选择[J]. 哲里木畜牧学院学报,1998,8(1):34-38.
[10] 宋喜芳,李建平,胡希远. 模型选择信息量准则AIC及其在方差分析中的应用[J]. 西北农林科技大学学报,2009,37(2):88-92.
[11]王 辉,刘志刚,符世伟. 湛江北部湾海域养殖墨西哥湾扇贝重量性状增长规律的研究[J]. 热带海洋学报,2007,26(5):53-59.
[12]郭华阳,李有宁,张 楠,等. 企鹅珍珠贝早期养殖生长性状的增长规律及生长曲线拟合研究[J]. 南方水产科学,2016,12(5):71-80.
[13]唐瞻杨,林 勇,陈 忠,等. 尼罗罗非鱼的形态性状对体重影响效果的分析[J]. 大连海洋大学学报,2010,25(5):428-433.
[14]Abolfathi M,Hajimoradloo A,Ghorbani R,et al. Compensatory growth in juvenile roach Rutilus caspicus:effect of starvation and re-feeding on growth and digestive surface area[J]. Journal of Fish Biology,2012,81(6):1880-1890.
[15]Velazquez M,Zamora S,Martinez F J. Influence of environmental conditions on demand-feeding behaviour of gilthead seabream (Sparus aurata)[J]. Journal of Applied Ichthyology,2004,20(6):536-541.
[16]Peres H,Santos S,Oliva-Teles A. Lack of compensatory growth response in gilthead seabream (Sparus aurata) juveniles following starvation and subsequent refeeding[J]. Aquaculture,2011,318(3/4):384-388.
[17]Ali M,Nicieza A,Wootton R J. Compensatory growth in fishes:a response to growth depression[J]. Fish and Fisheries,2003,4(2):147-190.[HJ1.66mm]
[18]刘志刚,王 辉,符世伟. 湛江北部湾养殖墨西哥湾扇贝的形态增长规律[J]. 水产学报,2007,31(5):675-681.
[19]邬思荣,刘志刚,王 辉. 湛江北部湾马氏珠母贝红壳色选育系生长模型研究[J]. 广东海洋大学学报,2011,31(3):16-24.
[20]Kuhi H D,Kebreab E,Lopez S,et al. An evaluation of different growth functions for describing the profile of live weight with time (age) in meat and egg strains of chicken[J]. Poultry Science,2003,82(10):1536-1543.
[21]Gamito S. Growth models and their use in ecological modelling:an application to a fish population[J]. Ecological Modelling,1998,113(1/2/3):83-94.
[22]邢黎峰,孙明高,王元军. 生物生长的Richards模型[J]. 生物數学学报,1998,13(3):348-353.
[23]颉晓勇,钟金香,李思发,等. 吉富品系尼罗罗非鱼选育系F6、F7和F8当年鱼生长对比研究[J]. 南方水产,2009,5(1):48-53.
[24]何小燕,白俊杰,樊佳佳,等. 大口黑鲈早期生长发育规律的研究[J]. 大连海洋大学学报,2011,26(1):23-29.
[25]索效军,张 年,熊 琪,等. 麻城黑山羊生长曲线的拟合与分析[J]. 江苏农业科学,2015,43(11):291-293.
[26]Chen X B,Liu H B,Su Y P,et al. Morphological development and growth of the freshwater mussel Anodonta woodiana from early juvenile to adult[J]. Invertebrate Reproduction & Development,2015,59(3):131-140.
[27]Urban H J. Modeling growth of different developmental stages in bivalves[J]. Marine Ecology Progress Series,2002,238(1):109-114.endprint
