巧用转化思想，解决图形问题

我们都知道“司马光砸缸”的故事，司马光巧用了转化的方法，成功解决了难题.让我不禁联想到，在解数学题中，用好转化的思想可以使问题化难为易，最近在学习“5.3展开与折叠”的过程中就遇到了这样一道题：

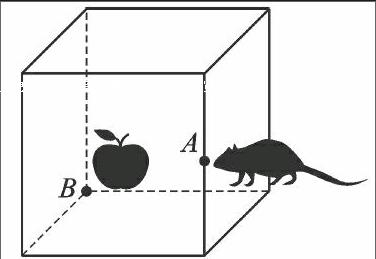
如图，一个无盖的正方体盒子棱长为12dm，外侧点A为所在棱的中点，点A处有一只小老鼠，盒子里内侧点B有一个苹果，老鼠的爬行速度是1dm/s，小老鼠最快用几秒爬到苹果处？

刚开始看到这题，我有点头疼，这两点不仅不在同一平面内，而且一个点在外侧，一个点在内侧，两个点完全没有联系.但我转念又想，老师常说再难的题目一定可以转化为我们学过的知识来解决.

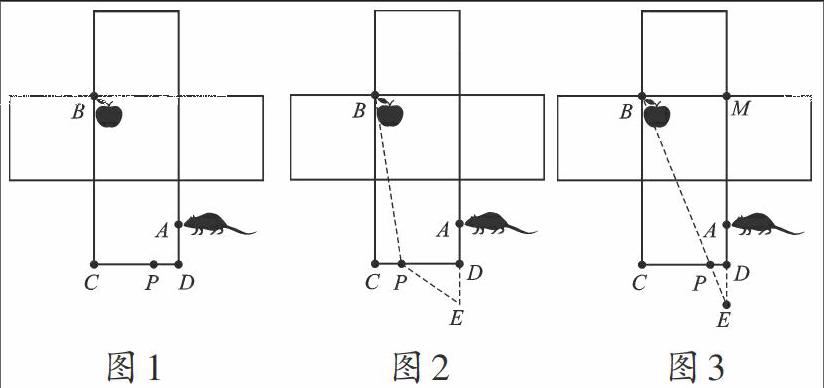
经过仔细思考和分析，我发现这道题可以通过把正方体侧面展开，将不在同一平面的两个点转化到同一平面来解决.于是，我将正方体盒子展开得到如图1所示的一个平面图形，设线段CD上有一点P，那么这道题可以转换为求点P到点A、B距离之和的最小值.这又让我犯难了，但我想到之前学过两个与“最短”有关的结论，分别是“两点之间线段最短”和“直线外一点与直线上各点连线中垂直线段最短”，那应该怎么转化呢？我灵机一动，将点A沿CD所在直线翻折得到如图2的平面图形，那么该题又转化为求点P到点E、点B最短距离之和，因为“两点之间线段最短”，所以应该如图3，连接EB，线段EB的长度就是所要求的最短距离.求解EB的长度让我想到了勾股定理的知识，根据作图可知2DE=BM=12dm，所以ME=2BM+DE=30dm，又因为BM=12dm，因此在Rt△EBM中，∠BME=90°，BM2+EM2=BE2，所以EB==dm，又根據t=得到t=s.答：小老鼠最快用s爬到苹果处.

其实不仅是上面这一道题，许多不熟悉的题目我们都可以结合已学过的知识合理转化，从而找到解题的金钥匙.

教师点评

在中学数学学习中，转化的思想不仅是一种常用的重要思想，也是一种解题和学习的基本思想，是将未知的、陌生的、复杂的问题通过演绎、归纳转化为已知的、熟悉的、简单的问题，从而使问题顺利解决的数学思想.可以说，中学数学的解题过程实际就是一个转化的过程.从光佳璐同学的学习反思可以看出，她是一个善于思考的同学，在解决问题的过程中充分运用了转化思想，将问题与所学知识进行最近联想，逐步找到了解决这个较为复杂问题的方法.正如她所说，合理应用这种思想，可以起到事半功倍的效果，是解题的金钥匙.

（指导教师：袁 芬）endprint