浅析接触网定位器长度与定位器坡度的选择

黄 河

浅析接触网定位器长度与定位器坡度的选择

黄 河

对接触网定位器的2种计算模型进行比较，找出了计算结果的差异，得出了定位器坡度计算方法。

接触网；定位器；定位器坡度

0 引言

接触网工程现场施工时，定位器坡度选择通常需按照安装通用图的说明进行。虽然安装图对拉出值范围、超高范围等均进行了说明，但实际工程中仍存在由于定位器坡度选择不当导致定位器抬升或导线工作面不正等问题。本文从定位器的受力状态分析入手，对定位器坡度和定位器长度的选择进行讨论。

1 定位器状态分析

1.1 定位器受力分析和计算

现以定位器为受力单元，以其受力平衡为前提，详细分析各个力的作用及大小和方向。假设：直线区段上，正定位拉出值a=200 mm；相邻跨距L=50 m；定位管坡度为0；导线线密度ρ=1.082 kg/m；1000型定位器重量Gd=1.68 kg（含定位线夹），长度LD=1 000 mm；导线张力T= 1 500 kg；定位器两侧吊弦间距Ld=4 500 mm。图1为定位器受力状态分析图[1]。

图1中，Fz为定位点所受之字力，其值为Fz=，由图可得

因为定位器受力并处于平衡状态，其合力应该在AB延长线上，则有

则定位器开口值为

图1 定位器受力分析

将设定数据带入式（1）—式（4）得直线区段D=371 mm（D2取12 mm）。

曲线区段上，设曲线半径为2 200 m，超高110 mm，定位器选用1200型（含线夹重量1.84 kg），则得出D=394 mm（D2取12 mm）。

直线与曲线区段D值与《时速200 km通化2009（1006）安装图》中的数值基本一致。在实际施工中，可根据式（1）—式（4）按照不同超高、曲线半径、定位器型号分别进行定位器坡度的计算，以减小后期调整工作量。

1.2 以定位器质点为中心的受力分析和计算

第1.1节中所采用的计算模型是将定位器整体归算至定位线夹处建立的，它无法反映定位器长度与坡度之间的动态关系，因而需要重新建立以定位器质点为中心的数学模型[2]（图2）。

图2 以定位器质点为中心的受力分析

由图2可得，定位器在上述力系的作用下保持平衡，承受平面一般力系，可写出定位器钩位置的力矩平衡方程为

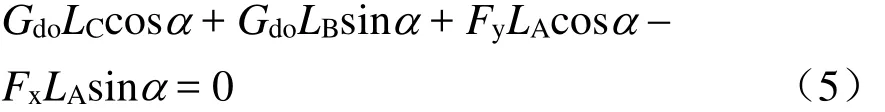
则

其中，Fx可按本文1.1节中水平分力计算，Fy为定位点两侧分别至第一吊弦点的导线重量。仍按第1.1节中相关计算数据代入式（5）、式（6）中，可得直线、曲线区段定位器开口值分别为366 mm、387 mm。

2 定位器长度与坡度的选择

通过以上分析可知，2种模型在直线区段定位器开口值数据相差5 mm，曲线区段相差7 mm。究其原因，以质点为中心的计算模型考虑了定位器质点处定位器自重对定位线夹处受力力矩的叠加效果，由于定位器长度的不同，质点的位置也随之变化，从而引起质点对定位线夹处的力矩也不同。在200 km时速内，由于受电弓抬升对定位器工况的影响相对较小，但时速超过250 km后，受电弓抬升明显加大，对定位器工况产生较大影响。

综上所述，在进行定位装置计算时，应先确定定位器长度，然后根据拉出值、定位器长度、线路情况等进行坡度计算，尤其是在缓和曲线区段，需根据不同超高确定相应定位器坡度（必要时还需考虑张力差的影响）。

3 结语

本文基于2种计算模型对定位器坡度进行了相应计算，并对计算结果的差异进行了比较分析，找出了产生差异的原因，得出了定位器坡度计算的控制点，可直接指导相关现场施工。

[1]黄河.高速电气化铁道受电弓抬升对定位器产生硬点的探讨[J].石家庄铁道大学学报（自然科学版），2013（s1）：115-117.

[2]于万聚.高速电气化铁路接触网[M].成都：西南交通大学出版社，2003.

The paper compares the two calculation models for steady arms for overhead contact system,finds out the differences between the two calculation results,obtains the calculation methods on steady arm gradient.

Overhead contact system;steady arm;gradient of steady arm

U225.4+2

B

1007-936X(2017)06-0034-02

10.19587/j.cnki.1007-936x.2017.06.009

黄 河.中铁八局集团电务工程公司，高级工程师。

2017-02-08