关于曲线积分计算的探讨
2018-01-05孟献青高晓燕
孟献青,高晓燕
(1.山西大同大学数学与计算机科学学院山西大同037009;2.山西大同大学教育技术学院山西大同037009)
关于曲线积分计算的探讨
孟献青1,高晓燕2
(1.山西大同大学数学与计算机科学学院山西大同037009;2.山西大同大学教育技术学院山西大同037009)
曲线积分是高等数学的一个重要内容,具有重要的实际应用。根据曲线积分与其它积分的关系,以及曲线积分的对称性,可以一题多解简化计算。
曲线积分;格林公式;对称性
高等数学是理工科学生的一门重要的基础课,具有高度的严谨性和抽象性,它在培养学生的思维能力和处理问题能力等方面,是其它任何课程无法取代的。高等数学也是理工科学生学习其他后续课程和解决实际问题的重要工具。许多学生在学习高等数学的时候会感到非常吃力,尤其在学习多元函数积分学时,由于涉及到的积分类型众多,各类积分之间又存在内在联系,学生难以得心应手。本文根据曲线积分与其它积分的关系,以及曲线积分的对称性,讨论曲线积分的计算。
1 两类曲线积分的联系与区别[1]
曲线积分分为对弧长的曲线积分和对坐标的曲线积分,两类曲线积分都可以通过各自的计算公式转化为定积分进行计算。两类曲线积分的区别在于:第一类曲线积分与曲线的方向无关,化为定积分后,要求下限小于上限;第二类曲线积分与曲线的方向有关,化为定积分后,下限是曲线的起点对应的参数,上限是曲线终点对应的参数,且两类曲线积分可以通过公式相 互 转 化 ,其 中(cosα,cosβ,cosγ)是曲线L在点 (x,y,z)处切向量的方向余弦。
2 曲线积分的计算
曲线积分可以根据曲线L的给出形式,根据公式进行计算,也可以根据积分的内在联系进行转化,如平面曲线满足一定的条件后,可用格林公式转化成二重积分进行计算,空间闭曲线可以用斯托克斯公式转化为曲面积分进行计算,且两类曲线积分亦可相互转化,使复杂问题简单化,因此在曲线积分的教学中要加强一题多解的训练及各类积分相互转化的训练,使学生能更好地掌握曲线积分的计算。下面,通过几个例题加以讨论。
例1计算曲线积分,其中L是x2+y2=R2在第一象限从(0 ,R)到(R,0)的一段弧。
解1利用直角坐标计算。

解2利用参数方程计算。
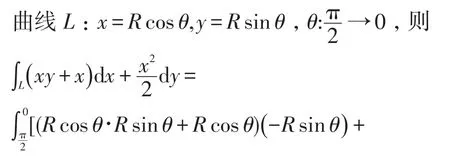

解3利用格林公式进行计算。令A(0,R),B(R,0),则围成闭区域D,且。由格林公式得

故

解4利用曲线积分与路径无关计算。
例2计算曲线积分

解1 利用直角坐标计算。
方 程 为 :z=0,x+y=1 或z=0,y=1-x,x:1→0;
方 程 为 :x=0,y+z=1 或x=0,z=1-y,y:1→0;
方 程 为 :y=0,x+z=1或y=0,z=1-x,x:0→1;
解2利用斯托克斯公式计算。

或

另外,如果被积函数具有奇偶性且积分区域具有对称性,可以利用对称性简化计算,尤其对于第二类曲线积分,可以避免因为没有考虑方向而出现的错误[2]。
例3计算 ∫L( )3x2+2xy+4y2ds,其中L是椭圆,且其周长为a。
解由于L关于x轴对称,且2xy是关于y的奇函数,故

例4 计算,其中,逆时针方向。
解对于积分,因为曲线L关于x轴对称且方向相反,函数是关于y的偶函数[3],所以;同理,对于积分,曲线L又关于y轴对称且方向相反,函数是关于x的偶函数,所以。

3 结语
通过上述例题发现,同一积分问题的解法很多,不同的解法体现了积分之间的内在联系,不同积分的相互转化,可以降低计算难度,另外,通过观察曲线积分的特征以及被积函数的奇偶性,可以简化计算,提高计算的准确率。
[1]同济大学数学系.高等数学(第七版)[M].北京:高等教育出版社,2014.
[2]江蓉,王守中.关于曲线积分与曲面积分教学的探讨[J].西南师范大学学报(自然科学版),2012,37(2):142-146.
[3]曹斌,孙艳.对称性在积分计算中的应用[J].吉林师范大学学报(自然科学版),2012,8(3):125-128.
Discussing on the Calculation of Curve Integral
MENG Xian-qing,GAO Xiao-yan
(School of Mathematics and Computer Sciences,Shanxi Datong University,Datong Shanxi,037009)
Curve integral is an important part of higher mathematics,and it has important practical application.According to the relation between curve integral and other integral,and the symmetry of curve integral,we can simplify the calculation by solving multiple problems.
curve integral;Green formula;symmetry
O172.2
A
1674-0874(2017)06-0012-02
2017-07-30
山西省高等学校科技研究开发项目[20121015];山西省青年科技研究基金项目[2013021001-1];山西大同大学大学生创新创业项目[XDC2017205]
孟献青(1979-),女,山西怀仁人,硕士,讲师,研究方向:图论及高等数学。
〔责任编辑 高海〕
