用能量法求解分布载荷作用下的静不定梁

张涛,吴晓

(1. 澧县第一建筑工程有限责任公司,湖南 澧县,415000;2. 湖南文理学院 机械工程学院,湖南 常德,415000)

用能量法求解分布载荷作用下的静不定梁

张涛1,吴晓2

(1. 澧县第一建筑工程有限责任公司,湖南 澧县,415000;2. 湖南文理学院 机械工程学院,湖南 常德,415000)

采用能量法求解了分布载荷作用下静不定梁的内力。算例计算表明,采用能量法求解分布载荷作用下静不定梁的内力,比积分法、力法、位移法等方法简洁。

能量法;分布载荷;静不定;梁;内力

由于静不定梁在土木、机械等实际工程中得到了广泛应用,因此,许多文献都研究了静不定梁内力的求解方法。文献[1]讨论了在数学推导过程中能量法的适用条件,证明了在线性条件下利用卡氏第二定理求解梁的内力时使用叠加原理是成立的。文献[2]采用能量法研究了超静定桁架杆件内力的求解。文献[3]利用拉普拉斯变换求解了静定及静不定梁的弯曲变形。文献[4]讨论了叠加法在计算梁的弯曲变形时的应用。文献[5]讨论了叠加法计算静不定梁的适用范围。文献[6]采用积分法研究了超静定梁的弯曲变形。文献[7]采用单位载荷法求解了静不定结构的位移。在材料力学、结构力学教材中,多采用积分法、力法、位移法、单位载荷法等方法研究分布载荷作用下静不定梁内力求解问题,但是上述方法的计算过程繁琐复杂。能量法由于着眼于宏观,具有计算过程简洁的优点,更易于推广应用。所以,本文将采用能量法研究分布载荷作用下静不定梁内力求解问题。

1 静不定梁的能量法求解

由材料力学可知,对于轴力可忽略的结构体系,其弯曲应变能表达式为

式中:U为应变能;M(x)为梁任意截面的弯矩;E为弹性模量;I为惯性矩;l为梁长。

把式(1)对外力求一阶导数可得卡氏第二定理表达式为

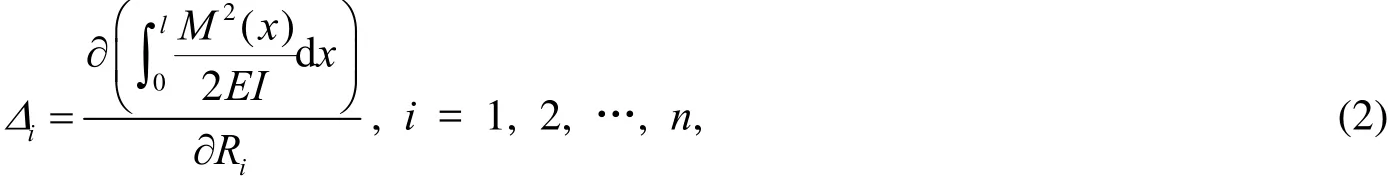
式中:Ri为作用在梁上的第i个力;Δi为第i个力Ri作用处的广义位移。

2 算例

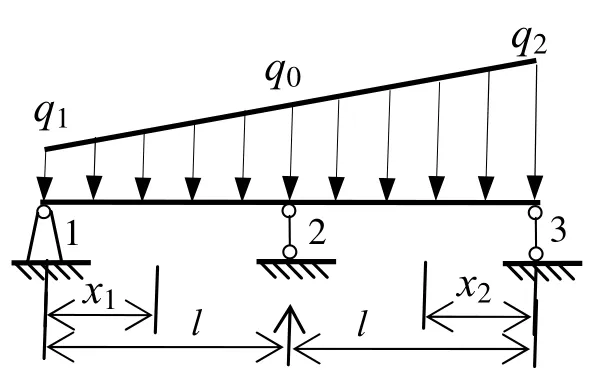
图1 连续梁

将U代入式(2),并利用Δ1=0、Δ3=0可得∂U/∂R1=2R1l3/3-q1l4/4-(q0-q1)l4/15=0;∂U/∂R3=2R3l3/3-q2l4/4+(q2-q0)l4/15=0。求解该式有R1=3q1l/8+(q0-q1)l/10,R3=3q2l/8-(q2-q0)l/10。当q1=q2时,R1、R3即退化为文献[8]给出的结果。

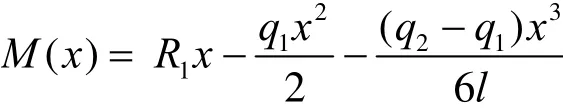
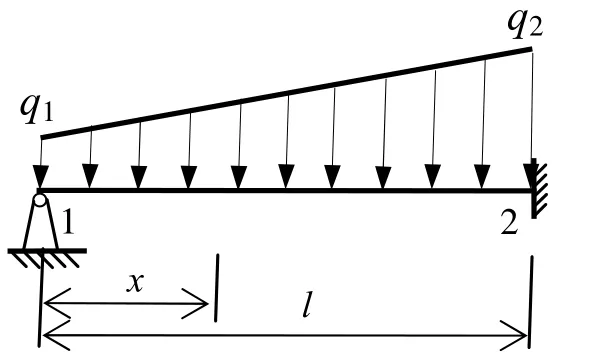
图2 一次静不定梁

将U代入式(2),并利用Δ1=0可得∂U/∂R1=2R1l3/3-q1l4/4-(q2-q1)l4/15=0,求解该式有R1=3q1l/8+(q2-q1)l/10。若q1=q2,R1即为文献[8]给出的结果。

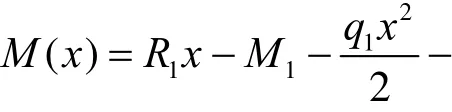
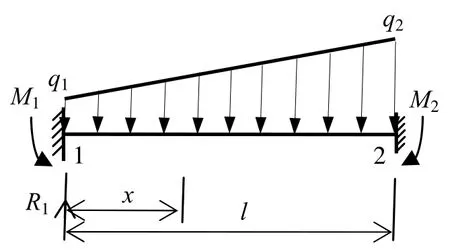
图3 三次静不定梁

3 小结

对以上计算结果进行分析可知,采用能量法研究分布载荷作用下静不定梁内力求解的问题,具有计算过程简洁的优点。若采用积分法、力法、位移法、单位载荷法等方法研究分布载荷作用下静不定梁内力求解问题,其推导运算过程极其繁琐复杂。其原因是积分法、力法、位移法、单位载荷法等方法研究分布载荷作用下静不定梁内力求解问题着眼于微观,在复杂条件下很难直接积分给出一个简单代数结果。而能量法研究分布载荷作用下静不定梁内力求解问题着眼于宏观,在复杂条件下仅限于积分求导即可得到简单代数结果,且计算过程有程序化的方法,易于工程设计人员掌握。

[1] 刘胜来,李金旺. 从数学推导过程讨论能量法的适用条件[J]. 力学与实践,2014,36(4):497-499.

[2] 王钟羡. 建立超静定杆系变形协调方程的能量方法[J]. 力学与实践,1998,20(6):55-56.

[3] 袁祥忠. 拉普拉斯变换求解梁的弯曲变形[J]. 力学与实践,1983,5(6):37-41.

[4] 李尧臣. 关于逐段变形效应叠加法的证明与讨论[J]. 力学与实践,2007,29(6):64-65.

[5] 蒋持平,严鹏. 计算梁与刚架位移两类叠加法的适用范围[J]. 力学与实践,2003,25(6):62-64.

[6] 王秀华,张春秋,门玉涛,等. 超静定梁变形计算的积分法[J]. 力学与实践,2009,31(4):79-81.

[7] 吴鹤华. 静不定结构求位移的方法及其证明[J]. 力学与实践,1998,10(2):47-50.

[8] S 铁摩辛柯,J 盖尔. 材料力学[M]. 胡人礼,译. 北京:科学出版社,1990:237-242.

Solving statically indeterminate beam under distribution loading by energy method

Zhang Tao1,Wu Xiao2
(1. Lixian First Construction Engineering Co Ltd,Lixian 415000,China;2. College of Mechanical Engineering,Hunan University of Arts and Science,Changde 415000,China)

The internal force of statically indeterminate beam under distribution loading is solved by energy method.The calculation results show that the energy method solving statically indeterminate beam under distribution loading is simpler than other methods such as integral method,force method and displacement method.

energy method;distribution loading;statically indeterminate;beam;internal force

O 341

A

1672–6146(2017)04–0066–02

10.3969/j.issn.1672–6146.2017.04.016

吴晓,wx2005220@163.com。

2017–04–21

湖南省科技计划项目(湘财企指[2011]65 号)；湖南“十二五”重点建设学科项目。

(责任编校:刘晓霞)