一体化智能电网中模块化功能单元的设计与实现
2018-01-04,
,
(1.四川水利职业技术学院,四川 成都 611231;2.四川明星电力股份有限公司信通公司,四川 遂宁 629000)
一体化智能电网中模块化功能单元的设计与实现
王珂涛1,廖兵2
(1.四川水利职业技术学院,四川 成都 611231;2.四川明星电力股份有限公司信通公司,四川 遂宁 629000)
随着现代电力系统复杂度的不断增加,其运行和控制相比传统电网而言面临着巨大的挑战。现代电力系统需要一方面实现各组件之间的协调运行;另一方面也要实现各自“即插即用”的模块化运行功能,由此实现在一体化智能系统引导下的模块化灵活运行模式。为此给出了一体化智能系统中模块化功能单元设计和实现的具体方法。首先,从模块化功能单元彼此之间协调运行的角度入手,以阻抗匹配特性作为系统稳定运行的判定标准;其次,从网侧交互稳定运行的角度入手,给出了对变换器网侧阻抗的估算方法。从理论上分析了上述方法的工作原理,而后利用Matlab/Simulink搭建了包含多台并联模块化单元的仿真模型,验证了上述所提出的模块化功能单元在一体化智能电网中的应用。
智能电网;模块化运行;阻抗匹配;高频谐波注入
0 引 言
随着可再生能源在电力系统中使用率的不断提高,传统的能源结构产生了巨大的改变。与此同时,人们对于环境污染、能源来源等方面需求的不断加深,进一步加速了能源形式的改变[1-3]。传统的电力系统以大型发电机为主要供电单元,而负荷多为感应电机、照明等常规负载形式,因此其在结构和复杂度方面相对现代电力系统而言更为简单。在现代电力系统结构中,不仅仅包含传统的发电和用电设备。从发电侧的角度讲,现代电力系统中一方面包含传统的发电机等供电单元,同时存在光伏、风电、燃料电池以及电池储能等多种新型的能源形式[4-6]。上述新型的能源形式不仅在时间尺度上和传统的发电单元具有动态过程上的差别,而且在输出功率方面存在随机性特点,即其可以提供的功率随着光照、风强等方面的因素会发生波动性变化。从负荷侧角度讲,现代电力系统在传统的感应电机、照明等常规负荷的基础上,增加了多种其他的负荷形式,其一方面包括具有阻抗性质的电阻型负载;另一方面包括具有恒功率性质的功率型负载,因此负载的稳态和动态过程也更为复杂[7-8]。
为了对上述日益复杂化的电力系统结构进行研究,实现有效的建模和控制,学者们提出了智能电网的概念,以便对现代电网进行有效调度和管理[9-12]。概括来讲,智能电网可以看作是对新型能源结构的区域化汇总,对传统电网的划分管理,在每一部分中实现电源侧和负载侧的功率平衡,同时满足稳定性运行的需要。需要指出的是,由于大量的新型能源形式,如光伏、风电等,广泛存在于智能电网之中,且其满足分布式接入的特点,因此智能电网具有分散化特点,在控制和建模等方面也更为复杂。与此同时,为了有效地管理各种新能源发电单元和各类新型负载,通常需要引入电力电子接口电路,利用并联运行的接口电路实现不同单元的分布式运行。在此基础上,为了实现对智能电网的有效管理,学者们提出了基于接口电路的多种分布式控制方法。具体来讲,分布式控制方法基于本地信息,实现模块化运行,满足各个模块之间以及模块和网侧之间的稳定性要求。
从功能的角度讲,模块化运行单元实现以下几方面的要求:
1) 实现本地电压及电流的控制,满足谐波和不对称度方面的标准要求;
2) 实现并网和离网运行控制,同时实现两种运行模式下的灵活切换;
3) 实现对系统整体稳定性的监测和在线实时评估,确保系统稳定运行;
4) 实现低电压穿越、本地无功补偿、黑启动等辅助性功能。
在满足上述本地功能的基础上,模块化单元还需要通过和网侧的信息交互,实现对网侧状态的监测,一方面实现在本地故障时的自身快速切除,以避免对外部大系统的扰动;另一方面也要在网侧出现故障时提供紧急支援,实现对网侧有功功率和无功功率的补给。
为了确保现代电力系统的可靠运行,在模块化功能单元的各项性能要求中,最为重要的一点在于系统稳定性的监测和评估,包括各模块化功能单元之间的稳定性判定;也包括模块化功能单元和外部电网之间的稳定性判定。在满足上述两方面稳定性要求的基础上,整体系统的供电质量才能得以保证[13-16]。
在分析现代电力系统结构和功能的基础上,首先介绍了模块化功能单元的需求和特点,而后着重分析了系统的稳定运行问题,包含两方面的内容,即各功能模块之间的稳定运行判定和模块与网侧之间的交互稳定性判定。在模块之间稳定性判定的过程中,引入了阻抗匹配的思想[17-18],利用分析得到的变换器的输出阻抗,利用阻抗匹配判定原理实现对并联运行的各模块单元稳定性的判断。上述方法对于多变换器系统的稳定性具有很好的检测和判定效果。通过对输出阻抗的实时检测,可以有效地判断多变换器系统的阻抗特性是否满足系统稳定性要求;同时,可以进一步计算得到系统的稳定裕度,确保整体运行效果满足设计要求。在模块和网侧之间稳定性判定的过程中,利用高频谐波注入的方法,实现对网侧阻抗的监测。当网侧阻抗过大的时候,本地系统的稳定裕度会大幅降低,因此会产生并网过程中失稳情况的出现。基于高频注入的方法,通过对本地模块化功能单元的输出电压和并网电流的傅里叶分析,提取所需要的频率分量,以实现对网侧阻抗的在线估算,进而实现对本地功能性模块单元和网侧交互过程中的稳定裕度的在线监测。
1 模块化单元功能分析
智能电网中的模块化功能单元适用于多种发电和用电组件,例如:光伏、风电、燃料电池、储能、主动性负载等,其示意结构如图1所示。从图1中可以看出,智能电网中的各个单元实现模块化运行,因此可以有效地降低控制复杂度。与此同时,各单元基本上均需要利用接口电路连接到公共母线,因此可以增加对电能质量额外的控制自由度,且可以实现各类辅助功能。
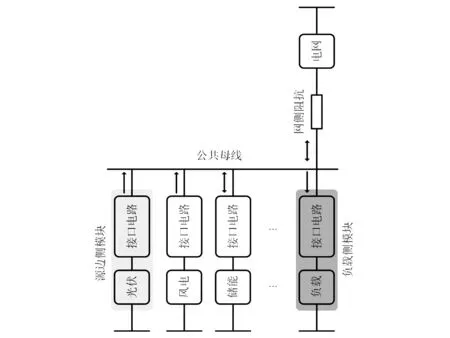
图1 智能电网中模块化功能单元的结构
从功能的角度讲,智能电网中的模块化功能单元一方面需要实现本地功能需求;另一方面需要实现本地和网侧协调的运行要求,示意结构如图2所示。为了实现对后续稳定性的评估,对图1的结构可以进行简化,简化结果采用戴维南等效电路,如图3所示。从图3可以看出,稳定性的判定需要从两方面进行,其一在于各个模块之间的稳定性评定,通过各模块之间输出阻抗的匹配关系实现;其二在于本地模块和网侧交互过程中的稳定性评定,通过观测网侧阻抗值实现。

图2 智能电网中模块化单元功能
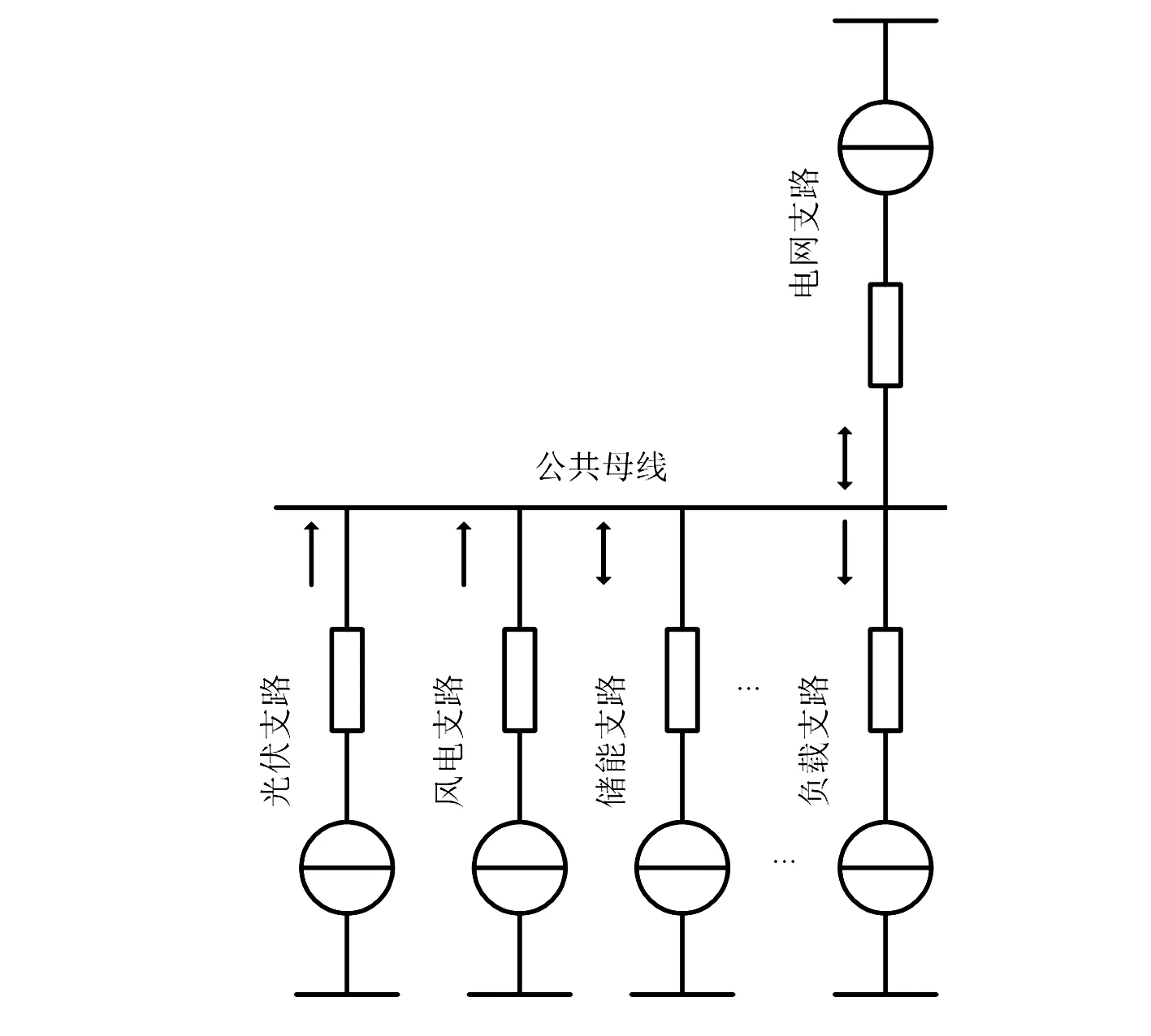
图3 模块化功能单元简化模型
2 模块化单元间稳定运行分析
为了实现对模块化功能单元彼此之间稳定性的评估,需要得到各模块的输出阻抗,进而利用阻抗匹配原理实现对稳定性的判定。
对于发电单元的输出阻抗,首先需要确定发电单元的控制结构。具体来讲,其控制结构如图4所示。其中,本地输出电压和电流采用比例-谐振(proportional-resonant,PR)控制,其结构形式如式(1)、式(2)所示:
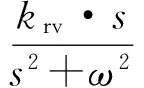
(1)
(2)
式中,Gprv和Gprc分别为电压和电流的比例-谐振控制器。
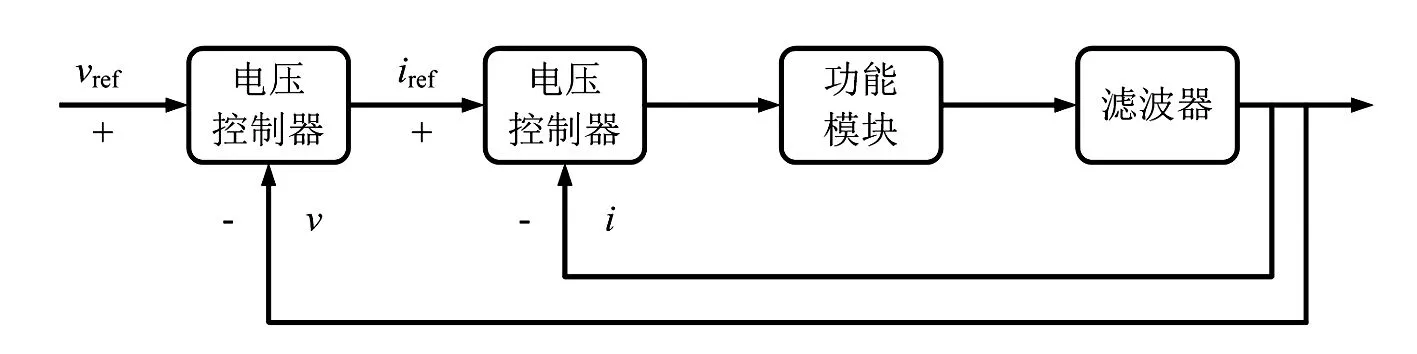
图4 模块化单元控制结构
在分析控制结构的基础上,可以推导得到模块的输出阻抗,其表达式为
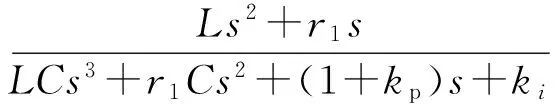
(3)
式中:L和C分别为滤波器的电感和电容值;r1为电感串联电阻;kp和ki分别为控制器比例和谐振项系数。
对于负载侧的阻抗,可以分为两方面推导得到:对于恒阻抗负载,其阻抗计算方法如式(4)所示;而对于恒功率负载,其阻抗计算方法如式(5)所示。
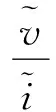
(4)
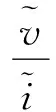
(5)
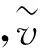
为了实现对于并联模块彼此之间稳定性的分析,此处需要使用阻抗匹配的判定方法。具体来讲,电源侧模块的阻抗和负载侧模块的阻抗需要代入式(6)所示的判定表达式。
Z=(1+Zload/Zsource)-1
(6)
若式(6)所示表达式的极点均在频域内的稳定区域,则系统阻抗匹配得以实现,即系统稳定性得以保证。此处所使用的是闭环极点稳定性判据。当且

图5 式(5)极点轨迹随模块输出阻抗变化情况
仅当系统所有闭环极点均处于s域左半平面时,系统稳定。以包含两个模块化单元的系统为例,在一个模块的输出阻抗变化的情况下,式(6)的极点变化情况如图5所示。可以看出,通过合理设计模块的输出阻抗,可以有效地确保模块之间的稳定性运行要求。
3 模块化单元和网侧交互影响稳定性分析
上面分析了模块化功能单元彼此之间的稳定性问题,下面进一步分析模块化功能单元和网侧交互部分的稳定性情况。
这里采用基于高频谐波注入的方法,即在变换器的输出电压中叠加具有很小幅值的高频谐波,通过傅里叶分析方法,提取模块输出电压和并网电流之中所需要的谐波分量,进而实现对网侧阻抗的在线监测。为了确保本地模块在网侧交互的过程中系统稳定,需要保证上述监测得到的阻抗值小于预设阈值。
注入的高频信号具有如下形式:
vinject=Ainjectsin(ωht)
式中:Ainject为注入信号的幅值(小信号);ωh为注入信号的频率(高频)。
而所使用的信号提取方法为

(7)
在此基础上,利用式(7)所示的信号提取方法,对模块输出电压和并网电流进行特定次谐波的提取,而后基于提取出的信号可以计算得到网侧阻抗,计算方法为
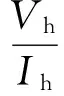
(8)
式中,Vh和Ih分别为模块输出电压和电流在注入谐波频率的幅值。
为了确保系统稳定,需要限定网侧阻抗小于预定阈值,即满足
Rg≤Rgmax,Lg≤Lgmax
(9)
4 仿真验证
为了对上述模块化功能系统进行有效验证,利用Matlab/Simulink搭建了系统级仿真模型。模型中包含4组功能模块,其中2组为源边侧模块,2组为负载侧模块,同时本地公共母线和外部电网相连。
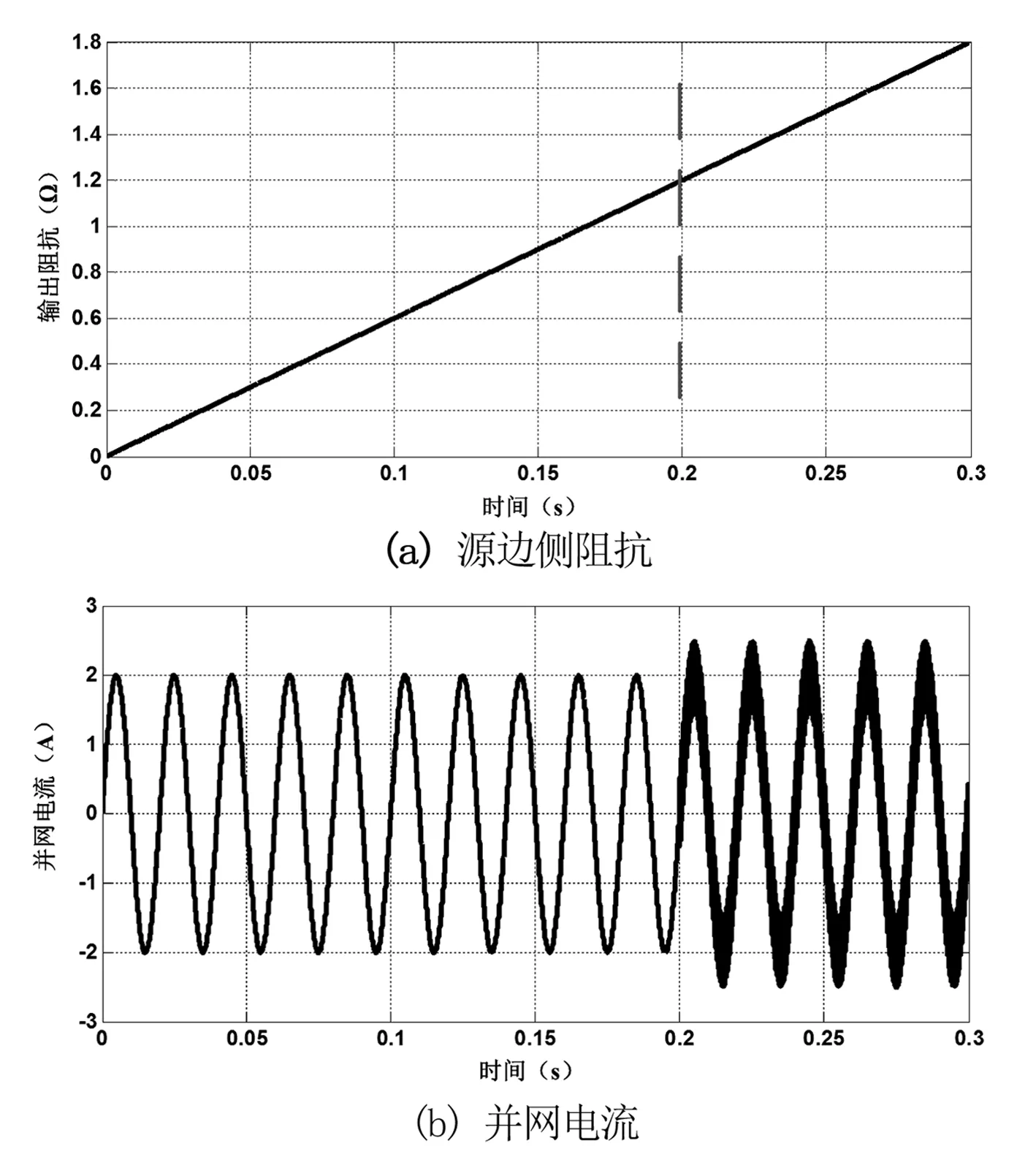
图6 源边侧阻抗增大时的并网电流波形
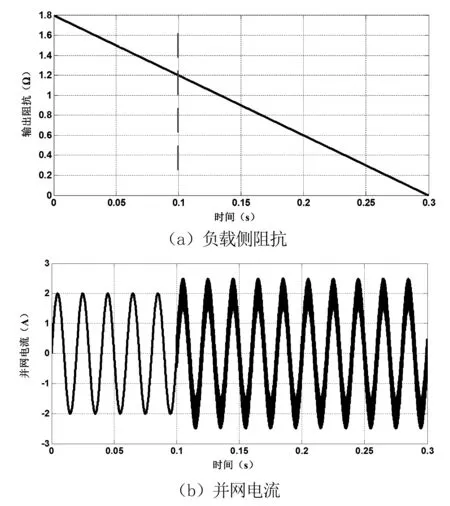
图7 负载侧阻抗减小时的并网电流波形
案例1:模块间的稳定性判定
如图6所示,当源边侧1号模块的输出阻抗增大时,系统在阻抗超过阈值时失稳;如图7所示,在负载侧3号模块的输入阻抗减小时,系统在阻抗超过阈值时失稳。
案例2:模块和网侧交互过程中的稳定性判定
利用所提到的网侧阻抗监测方法,计算得到的网侧阻抗如图8和图9所示。当网侧阻抗小于阈值时,如图8所示,系统运行稳定;而当网侧阻抗大于阈值时,如图9所示,系统运行失稳。

图8 网侧阻抗较小时的并网电流波形
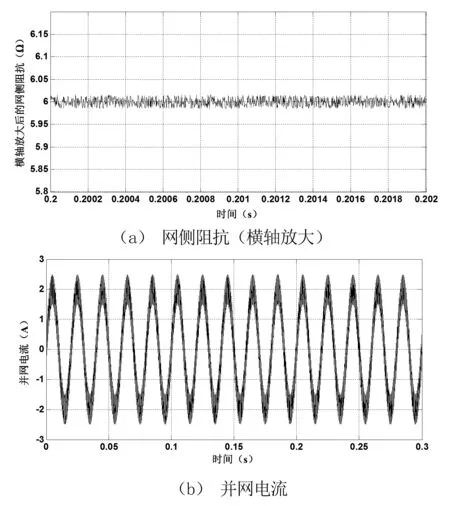
图9 网侧阻抗较大时的并网电流波形
5 结 论
在分析智能电网中模块化功能结构的基础上,对系统的稳定性进行了详细的分析。具体来讲,给出了各个模块之间的稳定性判定方法以及模块和网侧之间的稳定性判定方法。在模块化之间的稳定性分析过程中,利用阻抗匹配方法监测系统的稳定性;而在本地模块和网侧的交互过程中,利用监测网侧阻抗的方法对稳定性进行判定。其中,对于网侧阻抗的监测利用高频信号注入和傅里叶频域信号提取实现。仿真结果验证了模块化结构和稳定性评估方法的有效性。
[1] 陈树勇,宋书芳,李兰欣,等.智能电网技术综述[J].电网技术, 2009,33(8):1-7.
[2] 余贻鑫,栾文鹏.智能电网述评[J].中国电机工程学报,2009,29(34):1-8.
[3] 高明,李文云,顾全,等.一体化电网运行智能系统调度员驾驶舱的构想与实践[C].云南电力技术论坛论文集,2011:211-216.
[4] Yuan Wu,Lau, V.K.N.,Tsang, D.H.K.,et al. Optimal Energy Scheduling for Residential Smart Grid with Centralized Renewable Energy Source[J].Systems Journal,2014,8(2):562-576.
[5] Chenrui Jin,Xiang Sheng,Ghosh, P.Optimized Electric Vehicle Charging with Intermittent Renewable Energy Sources[C].IEEE Journal of Selected Topics in Signal Processing, 2014,8(6):1063-1072.
[6] Tian Zhang,Wei Chen,Zhu Han,et al.Charging Scheduling of Electric Vehicles with Local Renewable Energy Under Uncertain Electric Vehicle Arrival and Grid Power Price[J].IEEE Transactions on Vehicular Technology, 2014,63(6):2600-2612.
[7] Vlachogiannis J.G.Probabilistic Constrained Load Flow Considering Integration of Wind Power Generation and Electric Vehicles[J].IEEE Transactions on Power Systems, 2009,24(4):1808-1817.
[8] Tao Hong,Wilson J,Jingrui Xie.Long Term Probabilistic Load Forecasting and Normalization with Hourly Information[J]. IEEE Transactions on Smart Grid,2014,5(1):456-462.
[9] Xiao Z, Li T, Huang M.,et al.Hierarchical MAS Based Control Strategy for Microgrid[J].Energies,2010(3):1622-1638.
[10] Wencong Su,Zhiyong Yuan,Moyuen Chow.Microgrid Planning and Operation:Solar Energy and Wind Energy[C].Power and Energy Society General Meeting, 2010:1,7, 25-29.
[11] Xiaonan Lu,Guerrero,J.M.,Kai Sun,et al.Hierarchical Control of Parallel AC-DC Converter Interfaces for Hybrid Microgrids[J].IEEE Transactions on Smart Grid,2014,5(2):683-692.
[12] Yun Wei Li,Ching-Nan Kao,An Accurate Power Control Strategy for Power-Electronics-Interfaced Distributed Generation Units Operating in a Low-Voltage Multibus Microgrid[J].IEEE Transactions on Power Electronics,2009,24(12):2977-2988.
[13] Milasi,R.M.,Lynch A.F.,Yun Wei Li.Adaptive Vector Control for Voltage Source Converters[J].Control Theory & Applications, IET,2013,7(8):1110-1119.
[14] Guerrero,J.M.,Poh Chiang Loh,Tzung-Lin Lee,et al.Advanced Control Architectures for Intelligent Microgrids—Part II: Power Quality, Energy Storage, and AC/DC Microgrids[J].IEEE Transactions on Industrial Electronics, 2013,60(4):1263-1270.
[15] Wencong Su,Eichi H.,Wente Zeng,et al.A Survey on the Electrification of Transportation in a Smart Grid Environment[J].IEEE Transactions on Industrial Informatics, 2012,8(1):1-10.
[16] Xiaonan Lu,Kai Sun,Guerrero J.M.,et al.State-of-Charge Balance Using Adaptive Droop Control for Distributed Energy Storage Systems in DC Microgrid Applications[J].IEEE Transactions on Industrial Electronics, 2014,61(6):2804-2815.
[17] Guerrero J.M.,Garcia De Vicuna L.,Matas J.,et al.Output Impedance Design of Parallel-Connected UPS Inverters With Wireless Load-Sharing Control[J].IEEE Transactions on Industrial Electronics, 2005,52(4):1126-1135.
[18] Ciobotaru Mihai.,Teodorescu R.,Blaabjerg F.On-line Grid Impedance Estimation Based on Harmonic Injection for Grid-connected PV Inverter[C].IEEE International Symposium on Industrial Electronics, 2007:2437-2442.
With the development of the complexity of modern power system, its control and operation are facing great challenges compared to the conventional power system. Coordinated control of parallel functional units in modern power system should be satisfied. Meanwhile, "plug-and-play" should be achieved for each unit. Hence, the flexible operation and modular design should be realized in modern smart grid. In order to fulfill the above-mentioned requirements, the integrated design and implementation for modern smart grid is presented. Firstly, as viewed from the coordinated control of different modular functional units, the impedance matching is taken as the criterion. Secondly, as viewed from the interaction between the local inverter and external utility grid, the estimation method for grid impedance is proposed. Theoretical analysis is carried out, and then the simulation model composed of multiple parallel inverters is established with Matlab/Simulink, which is implemented to verify the effectiveness of the proposed method.
smart grid; modular design; impedance matching; high-frequency harmonic injection
TM71
A
1003-6954(2017)06-0039-05
王珂涛(1974),硕士、讲师、工程师,目前主要从事信息理论和信息新技术在电力系统中的应用研究及教学,重点研究方向为人工智能技术在电力系统中的应用以及电力系统故障分析与诊断。
2017-06-24)
