基于分布式电源与负荷双重不确定性的配电网综合规划研究
2018-01-04,,,,
,,,,
(1.国网四川省电力公司技能培训中心,四川 成都 611133;2.国网成都供电公司,四川 成都 610000;3.国网四川省电力公司经济技术研究院,四川 成都 610041)
基于分布式电源与负荷双重不确定性的配电网综合规划研究
杨力1,成思琪2,苏韵掣3,郑和平1,卢国栋1
(1.国网四川省电力公司技能培训中心,四川 成都 611133;2.国网成都供电公司,四川 成都 610000;3.国网四川省电力公司经济技术研究院,四川 成都 610041)
随着分布式电源大量渗入配电网,配电网在规划时要同时面临电源侧和负荷侧的不确定因素。首先,依据分布式电源出力与负荷的概率密度函数建立配电系统多状态模型,通过多状态潮流计算模拟它们的不确定性。其次,建立基于机会约束规划的分布式电源与配电网架综合规划模型,针对配电网规划问题的非线性、大规模等特点提出一种改进的遗传算法用于求解。通过对某地区实际配电网的计算分析,验证了所提算法具有良好的运行效率和收敛性能。算例结果表明,分布式电源的接入与网架结构调整相配合能够提升配电网的经济效益。
分布式电源;不确定性;多状态潮流计算;机会约束规划;改进遗传算法
0 引 言
配电网与大容量、远距离、结构清晰的输电网络不同,配电网节点众多、线路密集、改动频繁的特点导致配电网中存在相当多的不确定性,如负荷波动与增长的不确定性、线路间频繁转供导致的网架结构的不确定性等。具有波动性与间歇性特点的分布式电源(distributed generation, DG)接入配电网后将会进一步增加配电网中的不确定性,来自负荷侧与电源侧的双重不确定性给配电网规划带来巨大挑战。传统规划方法在一种确定的运行状态下得到的最优方案在其他系统状态下不一定仍是最优,从而降低甚至失去了最优规划的意义,甚至造成巨大的损失。
对于DG接入后的配电网规划问题,国内外已有许多研究成果,其关注重点主要集中在不确定性的处理与规划模型的建立上。
在不确定性问题的处理中往往面临着精确度与计算量之间的矛盾,文献[2-3]采取蒙特卡洛仿真来模拟DG与负荷的不确定性。虽然计算结果较为准确,然而若DG大规模渗入配网,系统中不确定因素进一步增加,求解规划问题时将很可能无法承受蒙特卡洛模拟所需的庞大计算量。文献[4-5]采用多场景法来分析系统中的不确定因素,这实质是综合若干个确定工况下的计算结果来分析系统的不确定性;由于场景数较少,各场景发生的概率制定也缺乏理论依据,导致该方法在不确定性的处理上不够精确。
在规划模型方面,国内外已有学者针对给定网架结构与变电站配置下的DG选址定类定容问题进行了研究。文献[6]以系统网损最小为目标,求解分布式风机与微型燃气轮机两种DG在配电网中的最优配置。文献[7]以年费用和运行费用最小分别作为上下层规划目标函数建立了基于机会约束规划的二层规划模型,实现配电系统中有功和无功功率的优化调度。然而,将DG接入与配电网网架结构调整相结合的综合规划研究尚不多见。文献[8]应用多智能体遗传算法对DG的位置、容量及配电网网架进行了整体优化,但并未考虑配电网中的不确定性。文献[9]先应用遗传算法求解DG的最优位置、容量,再运用模拟退火算法规划扩展网络,但将两者孤立求解对最终规划结果及算法计算效率都有影响。
针对上述文献中存在的不足,下面充分考虑分布式风机、分布式光伏发电以及负荷的不确定性,依据概率密度函数建立配电系统多状态模型,进而进行配电系统多状态潮流计算。根据计算结果建立基于机会约束规划的DG与配电网架综合规划模型,并提出一种改进的遗传算法用于求解,对某地区实际配电网的算例仿真验证了所提模型和方法的可行性和有效性。
1 不确定性分析
1.1 配电系统多状态模型
根据配电网中DG出力和负荷功率的概率分布,可将它们离散化为多种状态,则含DG的配电系统成为一个多状态系统。
采用文献[7]中的方法,将分布式风机离散化为Nw种状态。其中,风机出力为0时对应状态1;风机输出为额定功率时对应状态2;风机出力随风速变化时,先将风速离散化为Nw-2种状态,再求取各状态下风机的出力,状态划分结果见表1。
表1中:Pw为风机的输出功率;vi为切入风速;vr为额定风速;vo为切出风速;Pr为风机额定功率;
f(v)为风速分布概率密度函数。通过相似的方法可将分布式光伏发电离散化为Nz种状态,负荷离散化为NL种状态。采用Weibull分布描述风速特性,Beta分布描述光照强度特性,正太分布描述负荷特性。设Ph(l,m,n)是分布式风力发电出力为Pw(l)、分布式光伏发电出力为Pz(m)、负荷量为PL(n)时的系统状态,此状态发生的概率为F(l,m,n),则配电系统多状态模型可表示为
(1)
将此配电系统多状态模型代入规划计算,便能一定程度上反应配电网中分布式电源侧和负荷侧的双重不确定性,Nw、Nz、NL取值越大,系统总状态数越多,对不确定性的处理就越为准确,但计算量也越大。
1.2 配电系统多状态潮流计算
单次稳态潮流计算只能取得一种特定工况下系统的运行情况,这显然难以反映出配电网中的不确定性。这里借鉴随机潮流计算思想,对每种状态下的配电系统分别进行潮流计算,在最终输出的统计结果中可以直观地查看某条线路上的潮流有多大概率会超出它所允许的极限值,以及一些小概率极端状态下线路上最大潮流值是多少等详细信息。多状态潮流计算比单工况潮流计算更接近真实情况,也能更好地指导配电网的规划与设计。
2 配电网综合规划模型
考虑DG和网架结构的综合规划模型是含有多个随机变量的优化问题,采用机会约束规划的方法可以更好地处理随机变量的不确定因素。机会约束规划考虑到所做决策在不利的情况出现时可能不满

表1 风力发电机多状态模型
足约束条件,而采用一种原则:即允许所做决策在一定程度上不满足约束条件,但该决策使约束条件成立的概率必须不小于某一个足够小的置信水平。
2.1 目标函数
所设计模型以系统各状态依其发生概率加权平均后的系统经济性最优为目标,目标函数表达式为
(2)
式中:Closs为年化电能损耗费用;Cinv为年化设备投资及运行维护费用,由DG投资及运行费用、分段开关投资及运行费用、线路改造升级及运行费用3部分组成;Ctran为每年从上级电网的购电总费用。三者的详细表达式分别见式(3)、式(4)、式(5)。
Closs=ClPloss
(3)

(4)
(5)
式中:Cl为年化单位网损成本;Ploss为系统有功功率损耗;NDG为DG安装总数;CDGi为第i个DG的年化单位容量固定投资成本;PDGi为第i个 DG的安装容量;WDGi为第i个DG的检修、维护成本;Nl为支路总数,包括所有已有支路和待选新建支路;αlj为支路选择0-1变量,若为已有支路且无需改造,则α为 0,若为新增支路,则α为1;Clj为第j条支路的年化单位长度固定投资成本;Llj为第j条支路的长度;Wlj为第j条支路的检修、维护成本;Nst为开关总数;αst为0-1变量,若为已有开关,则α为0,若为新建开关,则α为1;Cs为新建一个开关所需的年化固定投资成本;Ws为一个开关的检修、维护成本;PAL为系统总负荷值;Poi为第i个DG的实际出力值。
2.2 约束条件
模型的约束条件分为概率机会约束和常规等式、不等式约束两类。考虑到不同状态下主要影响的是电网的运行情况,即电压、网损、支路潮流等,因此,将与之相关的约束条件采用机会约束的形式给出,具体包括支路功率概率约束、DG接入容量概率约束、节点电压概率约束。表达式分别见式(6)至式(8)。
(6)
P{PDGi(ξ)≤PLi}≥βDGi∈DDG
(7)
(8)

而模型中其他相对“确定”(即不受多状态影响)的约束条件,依旧采取传统的常规等式、不等式约束形式,包括功率平衡约束、DG安装个数约束和DG安装总容量约束。表达式分别为式(9)至式(12)。
(9)
(10)
(11)
(12)
式中:Pa、Qa分别为节点a注入的有功功率和无功功率;Gab、Bab、δab分别为节点a、b之间的电导、电纳与电压相位差;Nnode为配电网中节点总数;Ua、Ub分别为节点a、b的电压幅值;η为DG渗透率;PLdj为第j节点的有功负荷。
2.3 模型求解过程
遗传算法是从一种模仿生物界的自然进化过程演化而来的随机化搜索算法,以其通用性强、具有自组织、自适应和自学习性、不依赖问题模型等特性,在配电网规划中得到广泛应用。
配电网规划中往往可供选择的规划方案数量庞大,故需要大规模种群多代进化之后才能得到较理想的结果。然而标准遗传算法在高阶、长距离的进化过程中,交叉、变异操作有时会对最优个体起破坏作用,故这里在标准遗传算法的基础上加入精英保留策略[10],把种群进化过程中每代最好的个体保存至额外的个体空间里,并让它以100%的概率遗传至下一代种群。
配电网规划中可能遇到的另一个问题是:几种规划方案对配电网的影响在各个方面均很接近,故无论如何选取目标函数,都很难拉开几种方案的优劣差距。在这种情况下,若采取常规适应度函数的计算方法,群体中的高素质个体也就失去了在进化过程中的遗传优势。针对此问题,提出了一种适应度函数自适应策略,先将种群中的所有个体按优劣程度进行排序,再利用线性函数对最高级别个体到最低级别个体分别进行适应度赋值,具有相同适应度的个体共享适应度值。设所有个体已经按照优劣程度从高到低的顺序排序,最优个体的适应度值为Kf,则余下个体的适应度函数可由式(13)计算。
(13)
式中:F(x)为标准遗传算法中的适应度函数计算;F’(x)为改进后的适应度函数计算;Kp为种群中的个体数量。应用适应度函数自适应策略后,优质个体将有更大概率遗传至下一代;同时也增加了劣质个体被淘汰的速度,从而有效提高了遗传算法的优化性能。采用改进遗传算法求解规划模型的过程如图1所示。
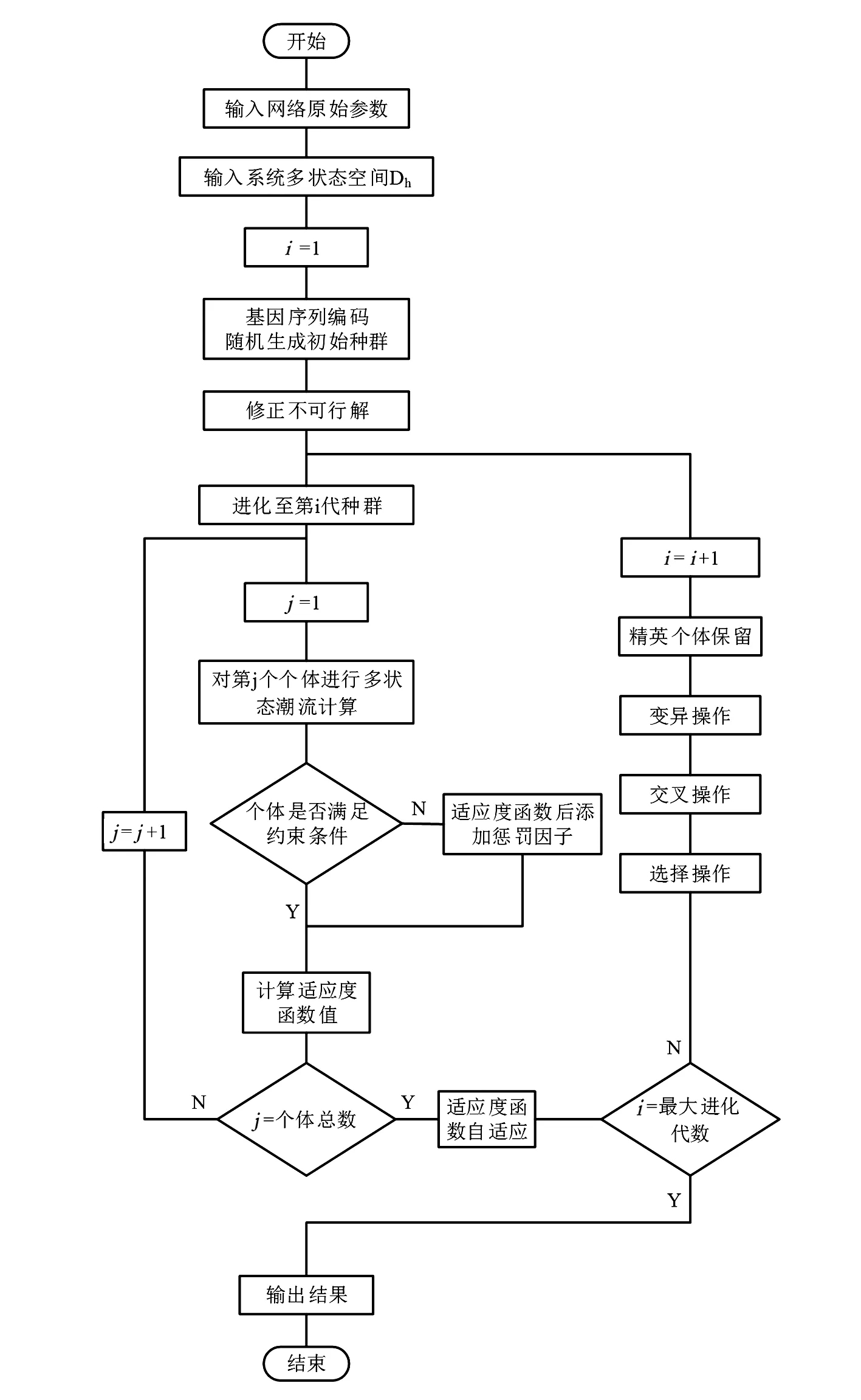
图1 规划模型计算流程图
3 算例分析
以某地区实际电网3条10 kV馈线作为算例进行计算分析,其网架结构如图2所示。3条馈线长度共计31.92 km,总供电半径约为 5 km。共有负荷节点152个,负荷共计16.06 MW和7.78 MVA,支路156条,其中包含3条待选新建支路及2条正常情况不投入运行的馈线转供支路。
下面针对以下几种规划方式进行分析:
1)在系统中选取不多于4个节点加入DG,DG 候选安装位置共有16个,已在图2中给出。DG候选安装类型有风机和光伏发电2种,分布式风机采用的型号为Northern Power公司制造的NPS 100-24,切入、额定、切出风速分别为3 m/s、7.5 m/s、25 m/s,额定功率为100 kW;光伏电池方阵组件选择PILKINGTON SFM144Hx250wp型,每个组件面积为2.16 m2,光电转换效率为13.44%,一个光伏电池方阵的组件个数为 400个,额定容量100 kW。风机单节点安装台数不超过3台,光伏电池方阵单节点安装数不超过3个。
2)在图2中的支路(1)、(8)、(11)所示位置新建线路。

图2 算例配电系统
3)改变系统中已有联络开关的状态,其中:常闭联络开关位于图2中标注的支路(2)、(3)、(4)、(6)、(7)、(9)、(10);常开联络开关位于支路(5)、(12),支路(5)和(12)为正常情况下不投入运行的馈线转供支路。
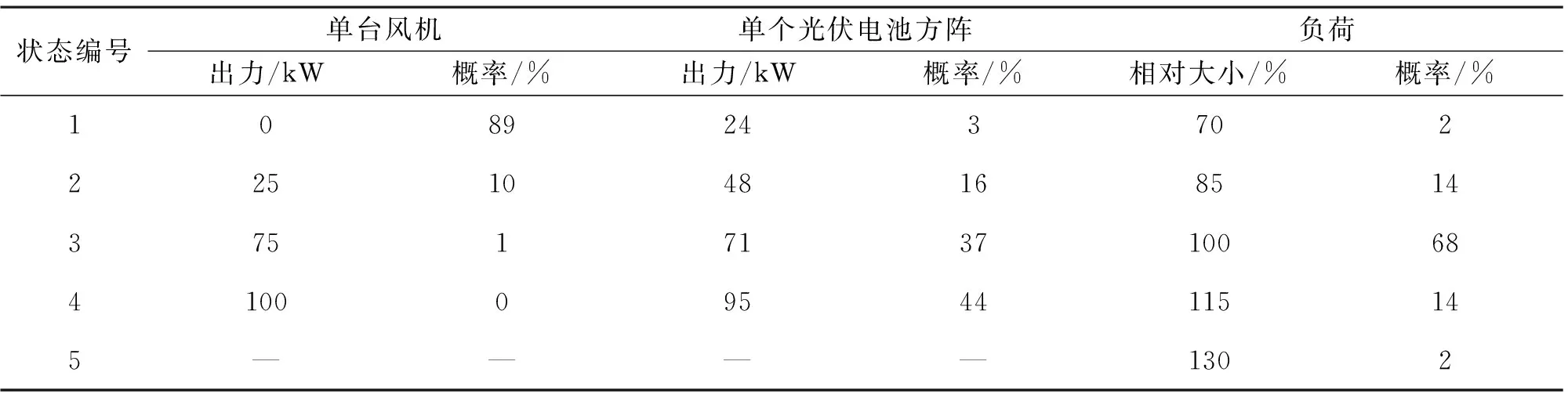
表2 多状态模型参数
为分析配电网中的不确定性,由规划区域气象观测数据计算风速、光照强度的概率密度函数参数,Weibull分布中k为1.35,c为1.65;Beta分布中α为2.16,β为1.35,最大光照强度为820 W/m2。基于以上结果建立算例系统多状态模型,其中分布式风机、光伏发电的不确定状态数为 4,负荷的不确定状态数为 5, 各状态下的具体参数见表2。
目标函数中的相关价格参考文献[11],模型约束条件里,概率约束中的置信水平均取0.9;节点电压上、下限分别为1.1 p.u.、0.9 p.u.,DG 最大渗透率为30%。
分别采用标准遗传算法和改进遗传算法对算例进行规划计算,种群迭代过程如图3所示。
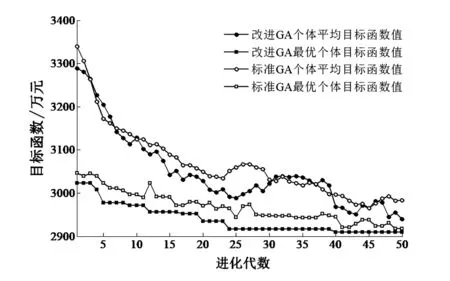
图3 算法迭代过程对比
由图3可知,改进的遗传算法通过精英保留策略解决了最优个体在进化的过程中遭到破坏的问题,通过适应度函数自适应策略增加了算法搜索过程中对优质个体的识别能力。由改进遗传算法求得的系统规划方案见表3,规划前后的费用比较见表4。
分析表中规划结果,DG在4个节点都接入最大容量300 kW,说明在一定渗透率的范围内,DG的接入可以提高系统的经济性,且DG接入的容量越大,提高越明显。4个节点接入的DG均为光伏发电,这可能是由于规划区域深处内陆山区,可利用的风能十分有限,因此光伏发电的效益将高于风力发电。4个DG接入节点都位于馈线A和馈线B上,这可能是由于这两条线路本身负载较重,且线路始端有一段同杆架设的长距离输电线路,在这段线路上将产生较大的电能损耗,而DG的接入,无疑将使这一情形得到改善。网架结构的调整与DG接入相配合,将馈线B上的11个负荷节点转由馈线A供电,使此区域内3条馈线的负荷量更加均衡。从费用上来看,接入DG后除增加了设备投资费用以外,电能损耗费用、购电费用分别降低了18.17%,6.10%,采用规划方案后此算例区域每年将节省210万元,比例达到6.73%。

表3 规划方案

表4 费用对比 单位:万元
4 结 论
1)依据概率分布对含DG的配电系统建立的综合多状态模型能较充分地反映配电系统中的不确定性。
2) 改进的遗传算法通过精英保留策略解决了最优个体在进化过程中遭到破坏的问题。通过适应度函数自适应策略增加了算法搜索过程中对优质个体的识别能力,其在处理含DG接入的配电网规划问题时具有良好的运行效率和收敛性能。
3)计及不确定性因素后,DG的接入与网架结构的调整相配合仍能够有效减小系统网损,提升配电网的经济效益。此外,不同类型DG的收益与其对应可再生一次能源的丰富程度有很大关联,故在DG选址定容定类的规划过程中,不仅应结合电力设备自身特点,规划区域的气象条件也应被纳入考虑范围。
[1] 杨毅, 韦钢, 周冰, 等. 分布式发电的规划模型及其求解方法[J]. 上海电力学院学报, 2010, 26(2): 113-118.
[2] 刘志鹏, 文福拴, 薛禹胜, 等. 计及可入网电动汽车的分布式电源最优选址和定容[J]. 电力系统自动化, 2011, 35(18):11-16.
[3] 高军彦, 麻秀范. 计及分布式发电的配电网扩展规划[J].中国电力, 2010, 43(2): 39-43.
[4] Vinicius F.Martins, Carmen L.T. Borges. Active Distribution Network Integrated Planning Incorporating Distributed Generation and Load Response Uncertainties[J].IEEE Transactions on Power Systems, 2011, 26(4): 2164-2172.
[5] 李亮, 唐巍, 白牧可, 等. 考虑时序特性的多目标分布式电源选址定容规划[J].电力系统自动化, 2013, 37(3): 58-63.
[6] 胡吟, 韦钢, 言大伟, 等. 分布式电源在配电网中的优化配置[J].电力系统保护与控制, 2012, 40(11): 100-105.
[7] 张璐, 唐巍, 丛鹏伟, 等. 基于机会约束规划和二层规划的配电网广义电源优化配置[J].电力系统自动化, 2014, 38(5): 50-58.
[8] 徐玉琴, 李雪冬, 张继刚, 等. 考虑分布式发电的配电网规划问题的研究[J].电力系统保护与控制, 2011, 39(1): 87-91.
[9] 王成山, 陈恺, 谢莹华, 等. 配电网扩展规划中分布式电源的选址和定容[J].电力系统自动化, 2006, 30(3):38-43.
[10] 闫若冰, 唐巍. 基于Pareto最优前沿的中压配电网多目标无功优化规划[J].电力系统保护与控制, 2010, 38(24):115-119.
[11] 白牧可, 唐巍, 张璐, 等. 基于机会约束规划的DG与配电网架多目标协调规划[J].电工技术学报, 2013, 28(10): 346-354.
[12] Aboelsood Zidan, Mostafa F.Shaaban, Ehab F.El-Saadany. Long-term Multi-objective Distribution Network Planning by DG Allocation and Feeders′Reconfiguration[J].Electric Power Systems Research, 105(2013): 95-104.
[14] 庄园, 王磊. 分布式电源在配电网络中优化选址与定容的研究[J].电力系统保护与控制, 2012, 40(20):73-78.
With the penetration of distributed generation (DG), distribution network planning is faced with the uncertainties coming from both sides of power supply and load. Firstly, according to the probability density function, the multi-state model of distribution system is established, which represents the uncertainties by means of multi-state power flow calculation. Secondly, a comprehensive planning model of distribution network with DG and network structure adjustment based on the chance constrained programming is proposed, which is optimized by an improved genetic algorithm. By calculating and analyzing practical examples of distribution network in an area, it is demonstrated that the proposed algorithm has a good efficiency and convergence performance. The results show that the economic benefits are effectively improved by comprehensive planning of DG and the network reconfiguration.
distributed generation (DG); uncertainty; multi-state power flow calculation; chance constrained programming; improved genetic algorithm
TM727
A
1003-6954(2017)06-0034-05
杨 力(1965),副教授,长期从事配电网自动化及可靠性研究。
2017-03-14)
