基于非参数估计的在线电压预测

(中国电力工程顾问集团西南电力设计院有限公司，四川 成都 610021)

基于非参数估计的在线电压预测

尤金
(中国电力工程顾问集团西南电力设计院有限公司，四川 成都 610021)

随着电网规模扩大、复杂度加深，对在线潮流计算确定节点电压提出严峻挑战，通过电压对无功的响应数据来快速精确预测电压发展趋势具有重要意义。提出基于非参数估计的节点电压快速预测方法，以系统负荷水平、无功激励为输入，节点电压为输出，以均方误差作为电压预测精度的指标，衡量预测效果。最后将该方法的预测结果与传统神经网络、自适应神经网络的预测结果作比较分析。通过IEEE 24节点系统标准算例验证表明，非参数估计方法具有较强的电压拟合能力和外推能力，其预测精度与神经网络算法的预测精度相当。

电压估计；BP神经网络；遗传算法；非参数估计

0 引 言

近年来随着中国国民经济的飞速发展[1]，电力负荷增长明显，电网规模日益扩大、结构日趋复杂，为传统在线潮流计算电压带来严峻挑战，但是随着数据采集技术、存储技术和处理技术的提高，使得通过大数据分析技术实现电压在线预测成为可能。

节点电压作为判断电网无功平衡和衡量电能质量的重要指标，其在线预测具有重要意义。目前关于电压预测的方法主要有最小二乘估计[2]、潮流估计[3]、灵敏度矩阵估计[4]以及公共耦合点电压预测[5]， 上述方法适用于采集部分信息的中小型网络。随着终端数据采集量的激增，可得到更加完善的信息；但这些信息在现有潮流计算方式下难以充分发挥作用，因此需借助统计学对数据价值进行充分挖掘，实现电压的在线预测。

借助统计学中非参数估计方法，提出基于Group-Lasso的电压在线预测方法，通过IEEE 24节点标准算例测试Group-Lasso方法的电压拟合能力和泛化能力，并将该方法的电压预测结果与传统神经网络、自适应神经网络算法的预测结果进行对比，验证了所提思路的有效性。

1 样本生成

产生样本的总思路是根据各负荷场景下变电站节点的电压和无功功率越限情况，按照九区图控制策略将电压、无功功率拉回至正常范围，并记录下该过程中负荷水平、发电机出力、变压器分接头挡位、电容器组投切量和节点电压，作为初始样本集。

1.1 负荷场景产生原理

产生负荷场景所涉及的负荷调整仅针对系统中的PQ节点进行，先大致构造日有功负荷曲线和日无功负荷曲线，如图1所示。

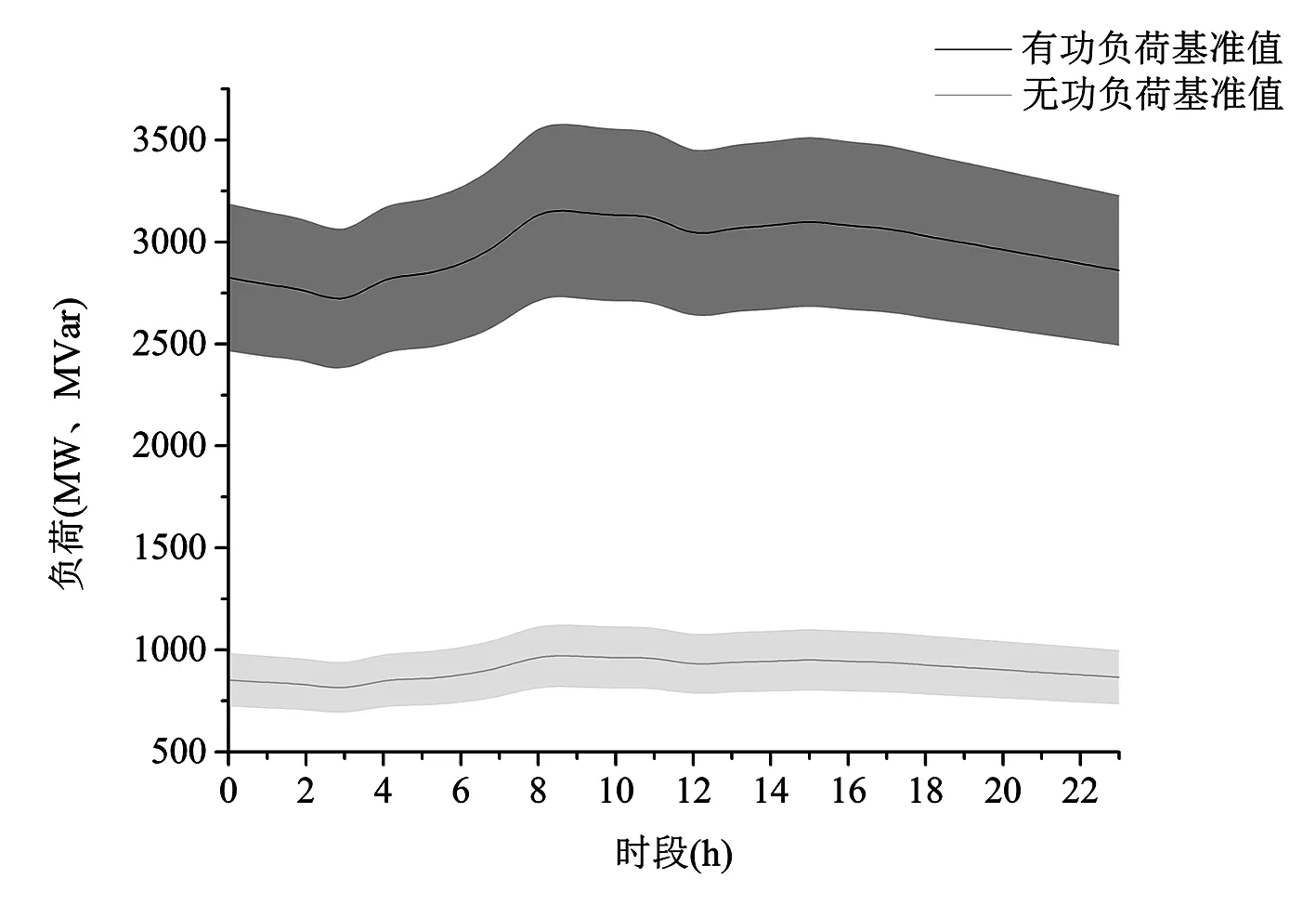
图1 日负荷曲线

图1中浅色曲线代表1天24 h的无功负荷基准值，深色曲线代表对应的有功负荷基准值。将浅色曲线乘以1.2作为无功负荷上限，乘以0.8作为无功负荷下限，形成图1中浅色的无功负荷带;同理可以得到图1中深色的有功负荷带。为了保证产生的负荷场景具有典型性，需在不同时段对应的两条负荷带内随机独立选取有功负荷值和无功负荷值。

1.2 调压机制

九区图控制策略按照固定的电压、无功上下限将整个控制区域划分为九宫格的形式。根据中国能源部制定的SD 325-1989《电力系统电压和无功电力技术导则》规定：变电所35～110 kV母线在正常运行时电压允许偏差范围为相应额定电压的[-3%,+7%]，对于220 kV及以下变电所，由电网供给的无功功率与有功功率比值范围为[0,0.33]。因此将九区图的电压上下限分别设为1.07和0.97，将无功功率与有功功率的比值上下限分别设为0.33和0，九区图控制策略下的设备动作规则参见文献[9]，此处不再赘述。

在1.1节构造的负荷场景中，如果变压器低压侧母线电压越限或高压侧母线无功功率越限，按照九区图控制规则进行设备调整，反之设备不动作。调压细则如下：对于每个负荷场景的电压无功控制最大调节次数不超过8次。220 kV变压器高压侧分接头调节范围为 [0.9,1.1]，每次调节步长为230×0.012 5。电容器组投切点均设置在变压器低压母线侧，且仅对PQ节点进行无功补偿，138 kV节点每次补偿步长为4 Mvar。系统中PV节点属于发电机节点，在实际运行中会自发地调整出力，因此需将发电机出力记录下来作为影响节点电压的一类因素。

2 基于Group-Lasso的非参数估计原理

所提两种预测模型的输入都是负荷场景、发电机出力、变压器变比以及电容器组投切量，统称特征属性，输出的目标属性均为节点电压标幺值。基于自适应神经网络的预测方法已在文献[10]中详细叙述，故不再赘述。

2.1 样本预处理

由于所涉及的数据维度较大，首先应排除与节点电压关联性不强的特征属性，采用非参数独立性筛选方法[11](nonparametric independence screening，NIS)进行弱关联特征属性的剔除，其基本思路是将各特征属性对目标属性依次进行以B-样条(basis-spline，BS)为基的非参数回归拟合，计算相应的残差平方和(residual sum of squares，RSS)并排序，RSS越大说明特征属性与目标属性关联度越小，最后根据关联度大小，逐一剔除弱关联特征属性。假设存在如下样本集：

(X1，X2，…，Xp，Y2，…，Yk)

(1)

其中，式(1)为n×(p+k)阶矩阵，表示该样本集包含n条独立样本、p个特征属性以及k个目标属性。对每个特征属性Xj进行BS展开，取Xj中第i条样本xij为例，其B-样条展开形式为

(2)

式中：aji1,aji2,…,ajin为xij经过BS展开后各项前的回归系数，由最小二乘法求得；bj4,bj5,…,bjn为插值节点，一般情况下在Xj的值域空间中按固定比例取值；n为自由度，它决定着fBij(xij)所含项数，n最小为3。

自由度的选取影响着回归模型的拟合精度，为寻找最优拟合效果对应的自由度，采用交叉验证(cross validation，CV)获取最优自由度，求取属性Xj回归函数的最优自由度步骤如下：

1)设定自由度取值区间 [3,n]，初始化自由度d=3。

2)将全部样本按顺序均分为m组，初始化i=1。

3)取自由度为d，以第i组以外的m-1组样本为训练集进行非参数回归。

4)以第i组样本为测试集，计算该回归模型的RSS。

5)若i=m，求得自由度为d时的m个RSS的均值，作为自由度d的RSS；若i≠m，则i自增1，返回3)。

6)若d=n，计算结束，提取每个自由度对应的RSS；若d≠n，则d自增1，返回2)。

7)对RSS进行排序，对应RSS最小者为该属性回归函数的最优自由度。

将各个特征属性按各自的最优自由度进行BS展开，展开的简化形式如下：

fBij(xij)=φBij1(xij1)+φBij2(xij2)+φBij3(xij3)+φBijn(xij)

(3)

用所有特征属性对各目标属性做回归拟合，计算其对应RSS值并由高到低进行排序，其中以RSS值有明显下降的拐点为分界线，分界线以前的特征属性表示与所考察目标属性关联性很弱，需剔除，保留分界线以后的特征属性作为后续步骤的输入样本。

对于NIS筛选后的特征属性，根据实际经验，某些特征属性变化幅度大，如负荷场景、发电机出力等;某些特征属性变化幅度小，如变压器变比。为了避免扭曲特征属性的实际影响力，需要对所有特征属性做统一的无量纲化处理，这里采用中心化处理方式：

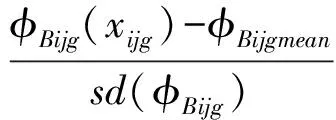
(4)

式中：φBijgmean为φBijg(xijg)的均值；sd(φBijg)为φBijg(xijg)的标准差，这样得到的φijg(xijg)就是中心化后的特征属性展开项。于是式(3)可改写为

(5)

式中，df为最优自由度，至此样本预处理完毕。

2.2 基于Group-Lasso的非参数估计

Group-Lasso回归模型通过将各特征属性的非线性函数相叠加来解决非线性问题[12]。其可加模型如式(8)所示：

(8)

那么Group-Lasso回归模型可表示为

(9)

式中，λ为惩罚参数。在矩阵稀疏化的过程中，当某些特征属性的惩罚参数λ压缩至0的时候，这些特征属性模长的权值就变为0，说明这些属性被回归模型自动剔除了。将式(5)所示的预处理样本带入Group-Lasso回归模型式(9)，可得

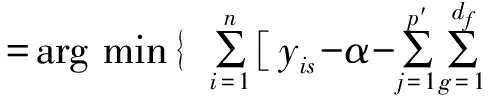
(10)

式(10)称为Group-Lasso回归模型的具体应用模式，最后该模型需要同时满足如下可识别条件：

(11)

基于Group-Lasso的非参数估计的总体流程图如图2所示。

图2 基于Group-Lasso的非参数估计流程

3 算例分析

以IEEE 24节点标准系统为例，采用所提两种方法与传统BP神经网络分别进行电压估计，分析三者优劣。IEEE 24节点系统的参数由文献 [13]给出，其系统结构如图3所示。

图3 IEEE 24节点系统结构

样本生成是基于Java调用BPA潮流计算程序实现的，总共产生10 000条样本，经人为剔除不变化的属性后，每条样本包含43个特征属性和15个目标属性，具体属性如表1、表2所示。

表1 样本特征属性

注：发电机出力中的PQ分别代表有功出力和无功出力，负荷场景中的PQ分别代表有功负荷和无功负荷，VQC中的C表示电容补偿，k表示变比，下标表示节点编号。

表2 样本目标属性

表3 3种方法的预测精度比较

将上述10 000条样本按75%和25%的比例分为训练集和测试集，将训练集分别提供给传统BP网络(BPNN)、自适应BP神经网络和Group-Lasso模型进行训练，即可得到关于节点电压的估计模型，再运用测试集测试模型的外推能力。这里采用均方误差(mean squared error, MSE)作为适应度函数，其表达式如下：

(12)

从表3中不难看出，以该样本量为前提，对电压估计精度最高的是GA-BPNN算法，BPNN与Group-Lasso的估计精度较为接近。另从表3中也能明确看到基于自适应遗传算法优化的BP神经网络无论是对训练集的拟合精度还是对测试集的估计精度都优于传统BP网络，提高了一个数量级的精度，说明将遗传算法和神经网络相结合确实得到了取长补短的效果。

4 结 语

从数字建模方式出发，绕过电力元件模型的建立，借助统计学思想，提出采用Group-Lasso算法对节点电压进行在线预测，并将预测精度与传统BP神经网络和自适应BP神经网络相比较，通过IEEE 24标准算例验证表明，GA-BPNN的电压预测精度最高，Group-Lasso与BPNN的预测精度相当，说明Group-Lasso算法具有较好的电压拟合能力和外推能力，可为传统的电压预测提供辅助手段。

[1] 鞠平，沈赋，陈谦．新背景下电力系统的建模思路[J]．南方电网技术，2016，10(3)：32-34．

[2] 王晨，童晓阳，王睿晗．有限相量测量单元下最小二乘估计的广域后备保护算法[J]．电力系统自动化，2015，39(20)：124-129．

[3] 邵黎，谢开贵，王进，等．基于潮流估计和分块负荷削减的配电网可靠性评估算法[J]．电网技术，2008，32(24)：34-37．

[4] 李卫东，宋家骅，武小梅．基于人工神经网络和灵敏度分析的快速电压估计[J]．东北电力学院学报，1994，14(1)：1-8．

[5] 张继红，贺智勇，邢军．利用公共耦合点电压估计的微电网逆变器下垂控制策略[J]．大电机技术，2015(1)：57-61．

[6] 陈伟根，滕黎，刘军，等．基于遗传优化支持向量机的变压器绕组热点温度预测模型[J]．电工技术学报，2014，29(1)：44-51.

[7] 马晋弢，杨以涵．遗传算法在电力系统无功优化中的应用[J]．中国电机工程学报，1995，15(5)：347-352．

[8] 史坤鹏，范国英，赵伟，等．基于BP神经网络的电网安全性预警系统开发[J]．南方电网技术，2013，7(6)：141-144．

[9] 厉吉文，潘贞存，李红梅，等．变电所电压和无功自动调节判据的研究[J]．中国电力，1995(7)：12-15．

[10] 尤金，刘俊勇，邱高，等. 基于自适应神经网络的电压快速估计[J]. 电力勘测设计，2017(1)：44-49.

[11] Fan Jianqing, Feng Yang, Song Rui. Nonparametric Independence Screening in Sparse Ultra-high-dimensional Additive Models[J]. Journal of the American Statistical Association, 2011, 106(494): 544-557.

[12] Huang Jian, Horowitz J L, Wei Fengrong. Variable Selection in Nonparametric Additive Models[J]. Annals of Statistics, 2010, 38(4): 2282-2313.

[13] Feng C L, Yuan Y H. IEEE Reliability Test System[J]. IEEE Transactions on Power Apparatus and Systems, 1979, PAS-98(6): 2047-2054.

With the expansion of grid scale and complexity, it is difficult to determine the node voltage by on-line power flow calculation, so it is very important to predict the trend of voltage quickly and accurately by the voltage response data. A fast voltage prediction method based on nonparametric estimation is proposed, which takes the system load level and reactive power as the input and the node voltage as the output. The mean square error is used as the index of the voltage prediction accuracy to measure the prediction effect. Finally, the prediction results of the proposed method are compared with those of the traditional neural networks and adaptive neural networks. The results of standard IEEE 24-bus system shows that the nonparametric estimation method has strong ability of voltage fitting and extrapolation, and its prediction accuracy is equivalent to the prediction accuracy of neural network algorithm.

voltage estimation; BP neural network; genetic algorithm; nonparametric estimation

TP183

A

1003-6954(2017)05-0001-04

尤 金(1990)，硕士，研究方向为电力系统数据挖掘。

2017-08-11)