基于MSN方法的洪涝灾害现场调查推算模型*
2018-01-04郭桂祯周洪建
郭桂祯,周洪建
(民政部国家减灾中心,北京 100124)
基于MSN方法的洪涝灾害现场调查推算模型*
郭桂祯,周洪建
(民政部国家减灾中心,北京 100124)
传统的空间推算方法对空间的均质性要求比较高,然而在洪涝灾害中,空间的均质性很难满足。该文将分层非均值地表推断方法(MSN)用于洪涝灾害损失现场调查,建立基于MSN的洪涝灾害现场调查推算模型,并用2013年黑龙江省汛期洪涝灾害验证本模型,总体推算误差控制在15%以内,较好的反应了整个灾区的受损情况。
洪涝灾害;MSN;房屋;倒损评估;现场调查;非均质;推算模型
1 研究背景及数据源
1.1 研究背景
洪涝灾害是一种严重威胁人类生存与发展的自然灾害,发生频率高,影响范围广,造成损失重。全世界每年因洪涝灾害造成的伤亡人数超过全部因自然灾害伤亡人数的65%,造成的损失超过所有因自然灾害损失的30%[1]。我国每年汛期都会发生洪涝灾害,给人民群众财产和生命安全造成巨大损失,2006-2015年,平均每年造成200多万间房屋不同程度受损,洪涝灾害已经成为人社会共同面临和关注的重大问题。
对洪涝灾害的评估也成为国内外学者研究的重点内容。传统的评估方法主要包括回归分析、模糊数学、GIS空间分析和实验分析风方法[2-11]。单九生等基于淹没水深和社会经济数据建立了BP神经网络模型洪涝灾害损失评估GIS模型,对洪涝灾害经济损失进行评估[12];葛鹏等改进传统的模糊数学方法,建立了洪涝灾害风险等级和损失等级评价数学模型,用于洪涝灾害风险评估[13];胡俊峰等建立了历史气象水文要素和灾情之间的洪涝灾害损失回归模型,用于洪涝灾害经济损失灾前预警评估和灾后损失评估[14]。洪涝灾害致灾因子复杂性和致灾方式多样行性决定了洪涝灾害损失评估模型的复杂性,导致上述评估模型精度较低,不能满足程度政府精准决策的要求,因此现场调查成为洪涝灾害损失评估的重要手段。
通常洪涝灾害的影响范围比较广,受人力资源约束,很难把所有的受灾区域都纳入到调查区域,因此,如何由较小的样本数量估计整个受灾区域损失就成为制约现场调查评估精度的重要因素。抽样理论的迅速发展为该问题的解决提供了有效的途径,它利用精度较高的有限样本点对其他未调查地区进行估计,从而达到对总体损失的估计。与经典抽样方法相比,空间抽样方法考虑了地理对象之间存在的自相关性,提高了对总体的估计精度。由Wang等提出的MSN(分层非均质地表均值估计)模型[15-16]在考虑相关性的基础上加入了地物对象可能存在的异质性特点,进一步提高了对总体的估计精度。本文将MSN模型引入到洪涝灾害现场调查评估,建立洪涝灾害现场调查总体推算模型。
1.2 数据源
本研究的数据主要包括2013年黑龙江省汛期洪涝灾害损失数据、降雨数据、河网密度空间分布数据、地形指数数据和分结构房屋存量数据,具体数据及其来源见表1。

表1 数据来源
2 模型方法
2.1 MSN模型原理
传统的空间推算方法(Kriging方法)对地表的均质性要求比较高,然而,在洪涝灾害中,地表的均质性很难满足。非均质地表推算模型(MSN),对洪涝灾害的复杂性具有较强的适应性。
假设空间场y(s),它是空间位置的函数(s是在区域上变化),具有非均质性,在数学上可以表示为一个均值和方差随空间变化的随机场模型。
E[y(s)|s∈h]=常数。
(1)
式中:E[·]表示均值算子。
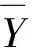
(2)
式中:yhi是h层内第i个样本点的值,whi是该点的权重。若要使是的无偏估计,则必需满足
(3)
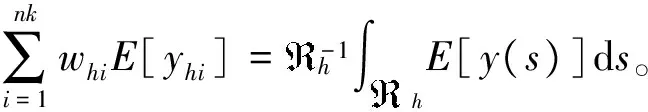
(4)
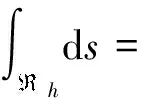
(5)
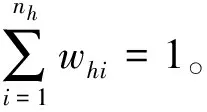
(6)
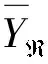
(7)
一般来说,该式对非均质性地表都是适合的。
根据上面的分析,空间属性特征地表的估计问题转变为寻找适当的权重系数whi(h=1;…,H:i=1,…,nh),它能同时满足(7)式无偏性和估计均值的方差最小:
(8)
针对分层非均质地表,满足条件的whi可以通过求解下面的方程组得到:
(9)
式中:μp是拉格朗日乘子,ah=h-1,ap=p-1。cov(yhi,ypj)是第h层中第i个样本点(si)与第p层中第j个样本之间的协方差,当h=p时,cov(yhi,ypj)表示同一层内特征属性之间的空间相关性(si∈h,sj∈h);当h≠p时,cov(yhi,ypj)表示不同层间特征属性之间的空间相关性(si∈h,sj∈p)。
2.2 基于MSN的洪涝灾害损失现场调查总体推算模型
(1)样本空间分层
根据洪涝灾害形成机理,日最大降雨量、累计降雨量、地形指数、河网指数是影响洪涝灾害的4个最重要指标,因此将这4个指标作为本模型分层依据。本模型采用k-means算法将样本空间进行分层,使得层内样本属性相差较小,层间样本属性相差较大。k-means算法是一种得到最广泛使用的基于划分的聚类算法,把n个对象分为k个簇,以使簇内具有较高的相似度。首先从总体中随机地选择k个对象,每个对象初始地代表了一个簇的平均值或中心;然后对剩余的每个对象根据其与各个簇中心的距离,将它赋给最近的簇;最后重新计算每个簇的平均值,这个过程不断重复,直到准则函数收敛。
(2)MSN模型实现
充分利用GIS的高效数据管理、丰富的可视化和强大的空间分析功能,选择了以Spatial.NET为基本组件的GIS开发平台进行灾害数据的管理和分析。同时,运用R语言的高效、快速统计建模优势进行底层关键模型的编写,实现洪涝灾害现场调查总体推算模型。首先根据选取的基础指标对空间进行分层,把受灾县分成不同的层;然后分析层内各县的相关性,从而得到层内所有县的损失;最后运用MSN模型分析层间的相关性,从而推算受灾区域内所有受灾县的损失(图1)。
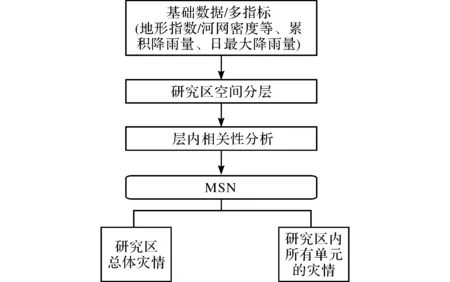
图1 模型架构图
3 案例验证
3.1 案例背景
本研究以2013年汛期黑龙江洪涝灾害为案例验证模型。2013年入汛以后,东北地区连续遭受强降雨过程,汛期平均累计降雨量达462 mm,较常年同期偏多26%,为1995年以来历史同期最多,加之上游水库泄洪,部分提防决口,给人民群众生产生活和社会经济造成了严重的影响,由于此次洪涝灾害致灾因子复杂,很难用一般的灾害损失评估模型计算灾害损失,因此采用现场调查方法估算此次洪涝灾害房屋倒塌和严重损坏数量。通过现场调查计算样本县的损失数据,之后用基于MSN的洪涝灾害现场调查推算模型估算整个灾区的损失。
3.2 模型计算
考虑灾情的严重程度和空间分布,选取五常、萝北、红星、抚远和林口五个县区为样本县,经过现场调查得出分县损失率如表2所示。
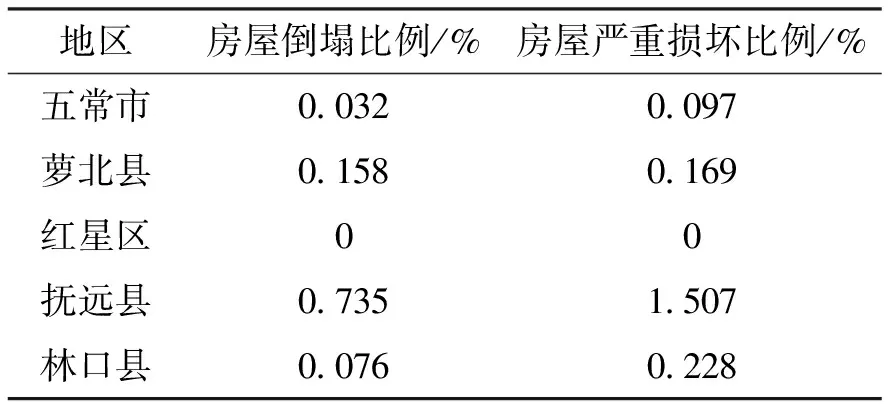
表2 现场调查样本结果
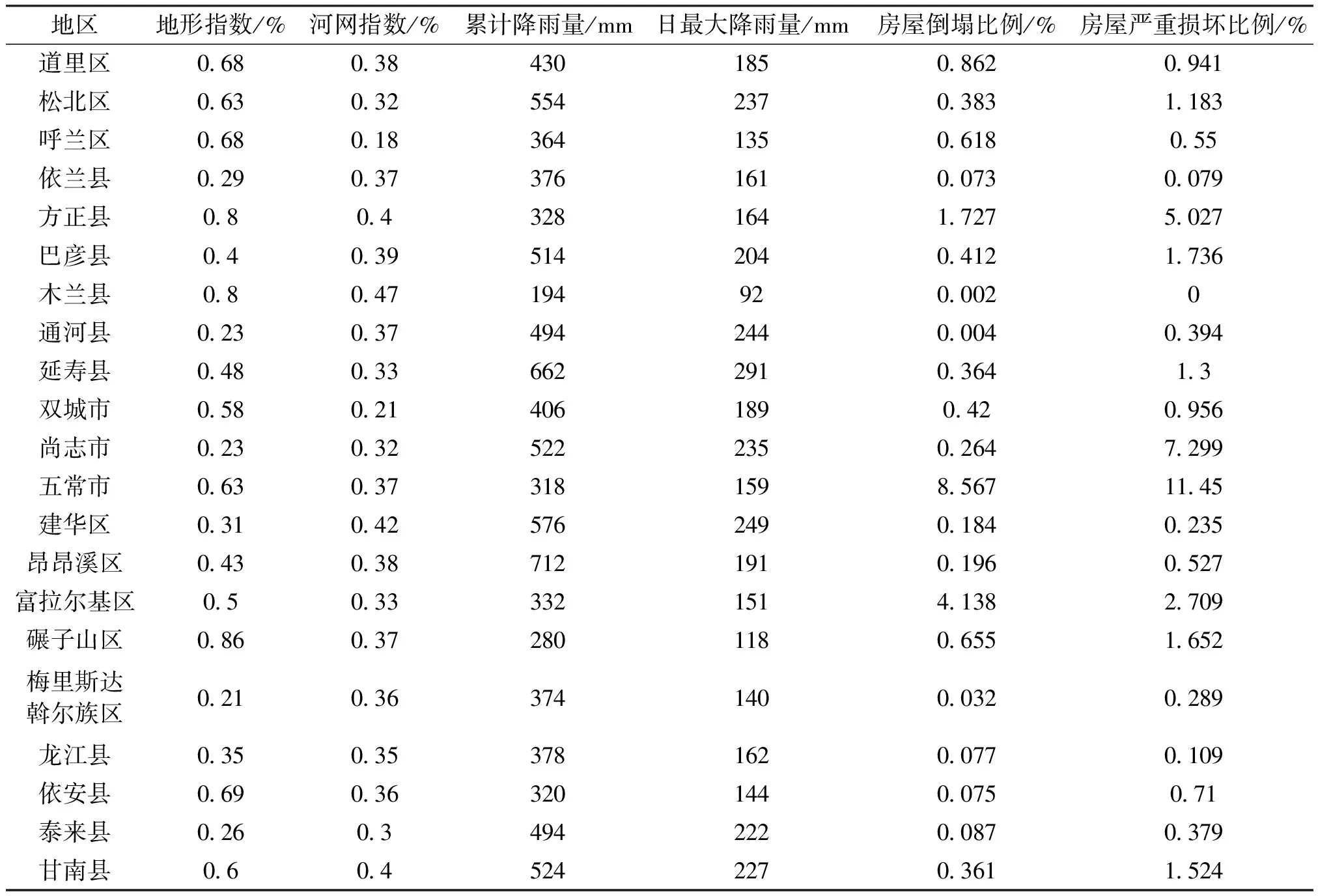
表3 部分受灾县基本指标及推算结果展示
把基本指标输入模型,得到黑龙江省置信区间为(0.3,0.8)全部受灾县的计算结果,标准差为0.15,部分受灾县的基本指标和计算结果展示如表3所示。
黑龙江全省房屋倒损数量计算值和灾情上报值对比如表4所示。
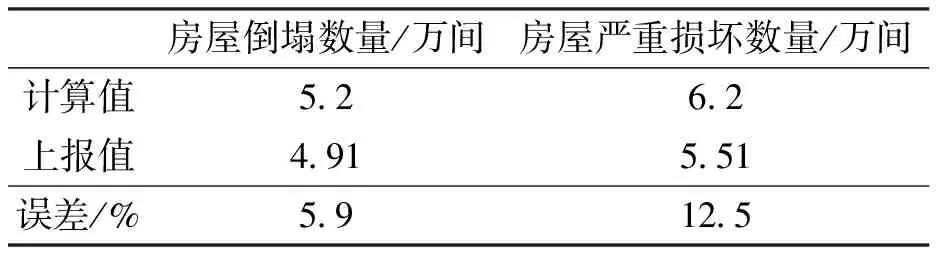
表4 总体结果对比
从计算结果来看,推算值和上报值的误差控制在15%以内,推算值能比较好反应整个灾区的损失情况。
4 结论
非均质地表推算模型(MSN)能很好的适应洪涝灾害的复杂性特点,把日最大降雨量、累计降雨量、地形指数、河网指数4个指标作为分层依据的基于MSN的洪涝灾害现场调查推算模型能比较精确的从样本损失推算空间总体损失,能为政府救助决策起到很好的指导作用。在下一步研究中,将进一步探索样本数量对模型精度的影响,从而达到更好的模型应用效果。
[1] Askew A J.Water in the international decade for natural disaster reduction [C]//Destructive Water :Water -Caused Natural Disasters, UK:IAHS Publ, 1997.
[2] 魏一鸣,金菊良,周成虎,等.洪水灾害评估体系研究[J].灾害学,1997,12(3):1-5.
[3] 李春.区域性洪涝灾害的灾情评估[J].自然灾害学报, 2004, 13(4): 75-81.
[4] 赵士鹏.基于GIS的山洪灾情评估方法研究[J].地理学报, 1996, 51(5): 471-479.
[5] 姜蓝齐,马艳敏,张丽娟,等.基于GIS的黑龙江省洪涝灾害风险评估与区划[J].自然灾害学报, 2013, 22(5): 238-246.
[6] 丁志雄,胡亚林,李纪人,等.基于空间信息格网的洪涝灾害损失评估模型及其应用[J].水利水电技术, 2005, 36(6): 93-101.
[7] 王艳艳.不同尺度的洪涝灾害损失评估模式述评[J].水利发展研究, 2002, 2(12): 66-69.
[8] 廖永丰,聂承静,杨林生,等.洪涝灾害风险监测预警评估综述 [J].地理科学进展, 2013, 31(3): 361-367.
[9] 李春梅,刘锦銮,潘蔚娟,等.暴雨综合影响指标及其在灾情评估中的应用.广东气象, 2008, 30(4): 1-4.
[10] 周瑶,王静爱.自然灾害脆弱性曲线研究进展[J].地球科学进展,2012,27(4):435-422.
[11] 扈海波,张艳莉.暴雨灾害人员损失风险快速预评估模型 [J].灾害学, 2013, 29(1): 30-36.
[12] 单九生,徐星生,樊建勇,等.基于GIS的BP神经网络洪涝灾害评估模型研究[J].江西农业大学学报, 2009, 31(4):777-780.
[13] 葛鹏,岳贤平.洪涝灾害承灾体易损性的时空变异——以南京市为例[J].灾害学, 2013, 28(1): 107-111.
[14] 胡俊峰,杨月巧.基于气象水文要素的洪涝灾害损失评估[J].南水北调与水利科技,2014,12(1):26-31.
[15] WANG Jinfeng,George Christajos,HU Maogui.Modeling spatial means of surfaces with stratified nonhomogeneity[J].IEEE Transactions on Geoscience and Remote Sensing, 2009,47(12):4167-4173.
[16] HU Maogui,WANG Jinfeng.A spatial sampling optimization package using MSN theory[J].Enviromental Modeling &Software.Machine learning,2011,26(1):546-548.
A Flood Field Investigation Caculating Method Based On MSN Method
GUO Guizhen and ZHOU Hongjian
(NationalDisasterReductionCenterofChina,Beijing100084,China)
Traditional spatial calculation method needs homogeneity, but homogeneity usually cannot be satisfied in flood disaster. We use Spatial Means of Surfaces with Stratified Nonhomogeneity method to build A Flood Field Investigation Caculating Method. At last, 2013 Heilongjiang Provence foold disater is uesed to verify the model; the error is under 15% which can indicate loss of the whole disaster area.
flood; MSN; house; damage assessment; field investigation; nonhomogeneity; calculation model
郭桂祯,周洪建.基于MSN方法的洪涝灾害现场调查推算模型[J].灾害学,2018,33(1):19-22.[GUO Guizhen and ZHOU Hongjian.A Flood Field Investigation Caculating Method Based on MSN Method [J].Journal of Catastrophology,2018,33(1):19-22.
10.3969/j.issn.1000-811X.2018.01.004.]
2017-03-29
2017-06-28
国家科技支撑项目(2013BAK05B02)
郭桂祯(1984-),男,山东聊城人,汉族,助理研究员,博士,主要从事自然灾害灾害损失评估研究.
E-mail: guoguizhen2008@126.com
X43;TV122.1
A
1000-811X(2018)01-0019-04
10.3969/j.issn.1000-811X.2018.01.004
