超声导波在H型钢结构损伤识别中的应用

2018-01-04王国锋李富才

振动、测试与诊断 2017年6期

关键词：翼板导波端面

王国锋，王敏，刘阳，孙杰，李富才，孟光

(1．上海交通大学机械系统与振动国家重点实验室上海，200240)(2. 中国船舶重工集团公司第704研究所上海，200031)

超声导波在H型钢结构损伤识别中的应用

王国锋1，王敏2，刘阳1，孙杰2，李富才1，孟光1

(1．上海交通大学机械系统与振动国家重点实验室上海，200240)(2. 中国船舶重工集团公司第704研究所上海，200031)

针对H型钢在损伤情况下对超声导波的影响，提出基于超声导波的结构健康监测方法，并探讨了应用超声导波检测技术在H型钢中对结构损伤识别的可行性及其识别能力。采用中心频率为87.5 kHz的波形为汉宁窗调幅3.5个周期正弦曲线作为激励波形，应用商业有限元软件ABAQUS对导波在H型钢构件中的传播进行了仿真，同时对无损伤以及有损伤的仿真模型进行实验验证。实验中利用压电材料锆钛酸铝(piezoelectric lead zirconate titanate，简称PZT)换能器来激发和接收在H型钢中传播的导波信号，借助于Morlet小波时频分析等方法对仿真和实验采集到的信号进行处理，并比较实验结果与仿真结果的吻合度。最后分析H型钢中损伤的大小等因素对损伤识别的影响，以及超声导波在H型钢中的损伤识别能力。

导波; Morlet小波；损伤识别；结构健康监测

引言

H型钢性能良好，广泛应用于建筑、工业、桥梁及机械等结构中，在工业生产、公共设施及交通等方面发挥着重要作用，而其结构健康状况直接关系到整个系统的安全性。H型钢的服役环境通常比较恶劣，随着服役时间的增长，受复杂工况的影响，不可避免出现损伤。近年来基于超声导波的无损检测技术，在结构健康监测方面取得很大的发展，成为结构健康监测领域重要的研究方向之一[1]。对于损伤的识别一般包括两个方面：损伤的位置识别以及严重程度判断。损伤的位置一般是通过计算导波的飞行时间(time-of-flight，简称ToF)和波速来确定[2]。在损伤类型确定的情况下，损伤的严重程度主要指损伤大小。孙凯等[3]研究厚梁结构中槽损伤位置、大小和疲劳裂纹等损伤对导波的影响。Alleyne等[4-5]研究板中切口损伤、复合板中的分层损伤等对Lamb波传播的影响。Lowe等[6-7]通过实验与有限元仿真等手段，研究板中裂纹对导波的作用规律，包括兰姆波的S0与A0模式等。

笔者重点研究H型钢损伤位置以及大小与导波信号的关系，包括导波信号飞行时间和波包幅值等有效的信号特征，分析这些因素对损伤识别的影响，为损伤大小识别奠定基础。

1 研究对象中导波信号的激发和接收

本研究对象为H型钢，其截面尺寸如图1所示，腹板厚度为8 mm，翼板厚度为10 mm，弹性模量为208 GPa，泊松比为0.28，密度为7 800 kg/m3。研究中对H型钢构件引入穿透性圆孔等损伤，采用Lc符号来表示损伤的真实位置(亦即损伤与传感器试件端面的距离)。研究中使用了损伤轴线距离相同(Lc=500 mm)、但损伤位置不同的试件，损伤位置分别为腹板的中轴线上的孔损伤、上翼板半侧的中轴线的孔损伤以及上翼板棱边的切槽损伤。

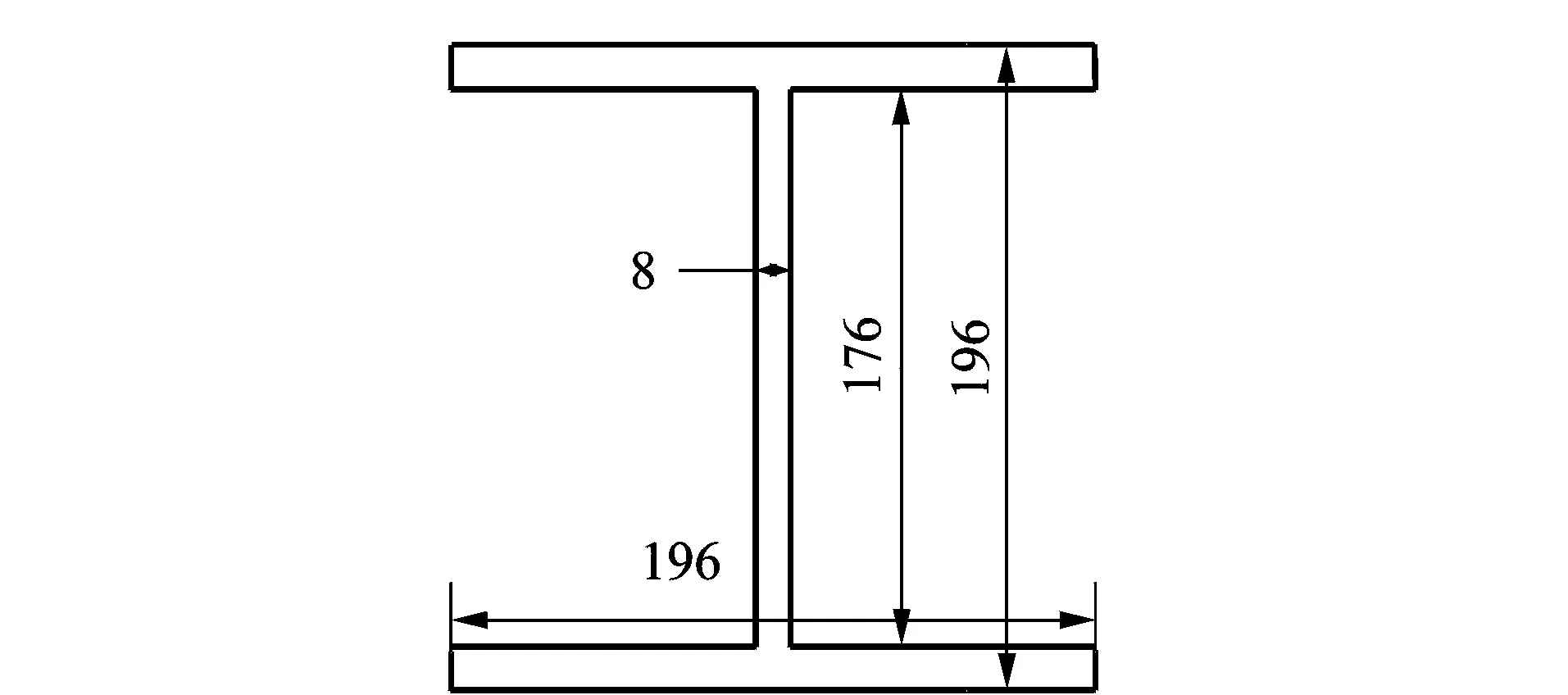
图1 H型钢截面尺寸(单位：mm)Fig.1 The section size of H-shape steel(unit:mm)

目前没有H型钢频散方程解析表达式，难以直接算出频散特征曲线。但是H型钢是由一个等厚度的腹板与两个等厚度的翼板组成，所以它的导波与板中导波具有一定的关联性，先从板中导波特性出发，选择合适的激励频率进行有限元仿真。

对上述的H型钢材料，Lamb波的频散曲线如图2所示，其中红色虚线为对称模式，黑色实线为反对称模式[8]。

如图2所示，Lamb波随着频厚积fd的增加，各个模式的群速度与相速度最终都收敛，除了A0与S0两种模式导波波速收敛于瑞利波波速，其他高阶模式导波波速收敛于横波波速。

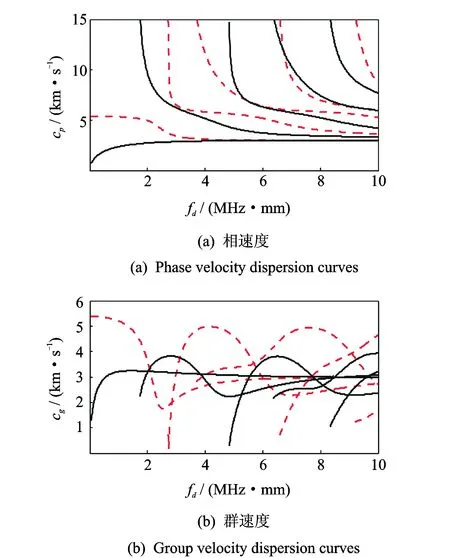
图2 Lamb波频散曲线Fig.2 Lamb wave dispersion curves

由于不同模式的传播速度不一致，当激励出的响应波信号模式数目较多时，传感器接收的信号含有多个模式成分，不利于损伤的识别和定位，故通常需要减少导波模式。在频厚积小于1.616 3 MHz·mm时，Lamb波只存在A0与S0两种频散的模式。由图 2可知，在此频厚积范围内，A0与S0两种模式导波分别存在一定群速度对频厚积非常敏感的区域，其中频厚积在(0～0.6) MHz·mm之间时A0模式频散比较严重，而频厚积在(1.2～1.616 3) MHz·mm之间时S0模式频散比较严重。检测信号应避开频散严重区域范围。从减少导波模式和降低频散效应影响的角度出发，应选择激励频厚积(0.6～1.2 M)Hz·mm之间。对于8 mm的翼板和10 mm的腹板，选择如图3所示的87.5 kHz波形为汉宁窗调幅的3.5周正弦曲线为激励信号。

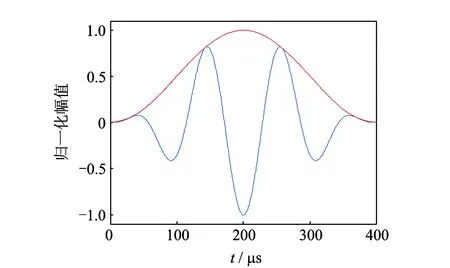
图3 汉宁窗调幅正弦波(87.5 kHz，3.5周)Fig.3 Hanning-windowed sinusoid(87.5 kHz,3.5cycle)

2 信号处理方法

鉴于实验中采集的信号受环境噪声的影响，所以需要对信号进行适当的处理以提取信号的特征。本研究通过低通滤波器处理信号以去除高频环境噪声的影响[9-10]。

笔者采用小波变换处理响应波信号以获得信号的时间-频率的关系。小波变换的基本思想是：对信号加窗，窗口大小不变、形状可变，是一种时间窗和频率窗都可以改变的时频分析方法。考虑小波母函数与激励信号的相似程度，笔者采用以Morlet小波(见图4)为母函数的连续小波变换对导波信号进行处理。

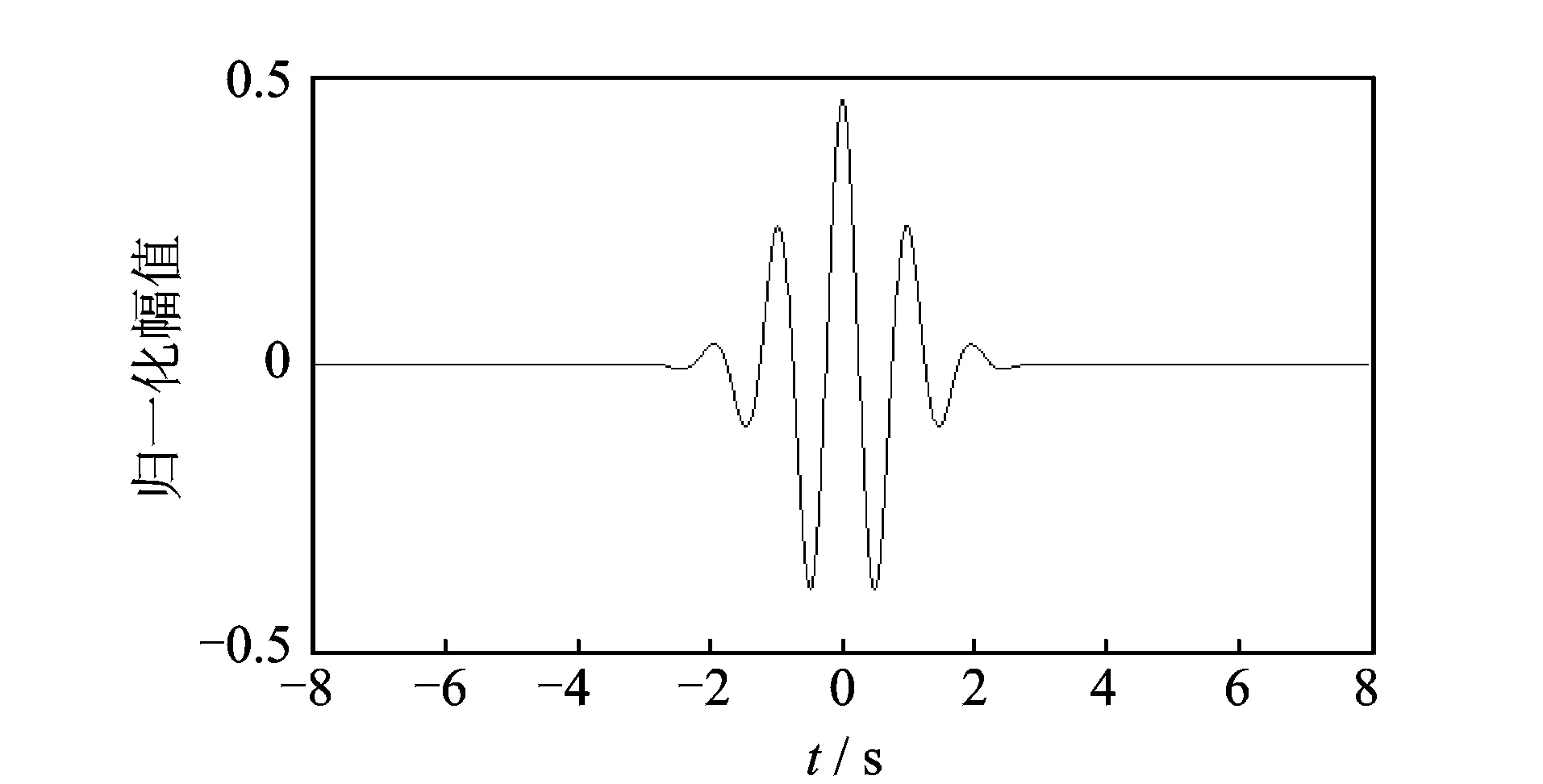
图4 Morlet小波Fig.4 Morlet wavelet

在小波变换中小波的尺度与频率有如下的转换关系

Fa=Fc/SΔT

(1)

其中：Fa为对应尺度的假拟频率;ΔT为采样周期；Fc为小波的中心频率；S为尺度。

将经小波变换后得到的时间、频率及相关系数绘制成等高线图，能够清晰地看出故障损伤的位置。例如损伤在H型钢的腹板中轴线的信号图与经小波变换后得到的等高线图，如图5所示。

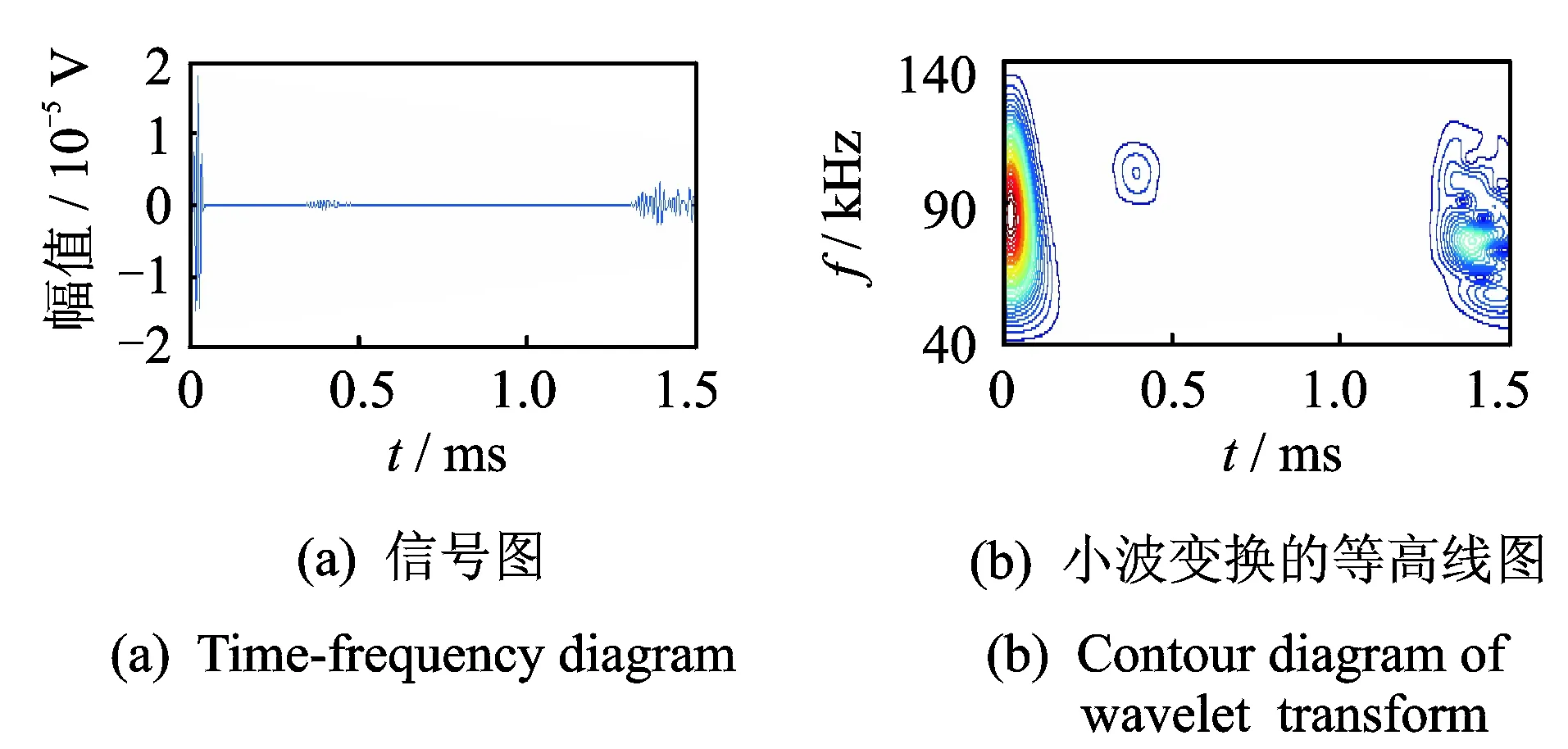
图5 腹板中存在孔损伤的H型钢Fig.5 Hole-damage in the web of H-shape steel

3 仿真与实验

本研究采用PZT晶片来激发和接收在H型钢构件中传播的相应波。PZT晶片具有双向压电效应，所以可以作为作动器和传感器。选用尺寸为20 mm×5 mm×1 mm的块状PZT。对于作动器位置分别选取如下：a.在腹板端面中间对称位置的20 mm×5 mm 范围内A1和A2施加相反的激励信号(以下简称腹板反对称激励)；b.在腹板端面中间对称位置的20 mm×5 mm 范围内A1和A2施加一样的激励信号(以下简称腹板对称激励)；c.在腹板端面中间位置的20 mm×5 mm 范围内A1施加激励信号(以下简称腹板单侧激励)；d.在翼板端面正中间位置的20 mm×5 mm 范围内A4施加激励信号(以下简称翼板中间激励)；e.在翼板端面一侧A3中间位置的20 mm×5 mm 范围内施加激励信号(以下简称翼板一侧激励)。激励信号如图2所示。对于传感器的位置分别选取如下：a.在腹板端面中间位置的一侧20 mm×5 mm 范围内S1(以下简称腹板接收)；b.在翼板端面一侧中间位置的20 mm×5 mm 范围内S2～S5(以下简称翼板一侧接收)。具体的激励与接收位置如图6所示。

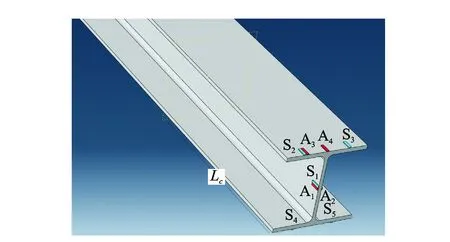
图6 作动器与传感器的位置Fig.6 The location of the actuators and sensors

3.1 仿真算例

在ABAQUS软件平台上选用三维实体8节点缩减积分单位(C3D8R Element)，采用ABAQUS Explicit求解器，进行动态有限元分析，对上述H型钢导波的传播特性进行仿真，并用删除单元的方法来模拟损伤的存在。通过该方法能很容易实现损伤深度或者厚度的变化，而不影响总体网格布局、编号等，从而为研究损伤大小变化对信号的影响奠定基础。

在对导波传播进行有限元仿真过程中，为了保证模拟相应导波波长在传播过程中的空间迭代产生的误差较小，减少由于网格划分引起的误差，防止计算结果发散，对仿真过程的时间和空间分辨率有严格要求，即

Le≤λmin/10

(2)

其中：λmin为最小波长；Le为最大网格尺寸。

此仿真过程中最大的网格尺寸为2.16 mm，而激励频率为87.5 kHz时，最小波长约为40 mm，满足式(2)。

仿真过程中，每增加时间Δt，新进入网格的计算区域应大于导波增加的传播范围。为了使算法稳定，需限定计算的时间步长，其大小需满足

Δt≤Lmin/cL

(3)

在此仿真中，时间步长为5.0×10-8s，最小网格尺寸为1.91 mm，纵波波速为5 848.0 m/s，满足要求。

在ABAQUS中通过施加集中力模拟PZT通电后由于逆压电效应产生应力、应变，在S1～S5处模拟PZT接收的信号，其中各个传感器的位置如图6所示。通过上述5种激励方式，其中腹板反对称激励的导波传播情况如图7所示。

通过仿真结果可知，H型钢的导波与板中导波具有一定的关联性，导波传播都是以激励为中心的圆形向外传播，H型钢中在未经边界面反射回来的导波成分与平板类似，从而验证了基于Lamb波的理论进行分析的有效性。

仿真中考虑了腹板与翼板的差异，分别在腹板与翼板中各自进行损伤的识别(以直径为8 mm的孔损伤为参考)。作动器激励的位置与传感器接收的位置也决定了导波传播的路径。因此必须考虑激励与接收位置对识别的影响，通过仿真腹板与翼板损伤在对上述5种不同激励条件下分别在腹板与翼板的接收情况。

图7 腹板对称激励下的导波传播情况Fig.7 Guided wave propagation under web symmetrical excitation

仿真对于腹板与翼板损伤在不同激励与接收条件下的导波情况如图8所示，其中(a)与(b)是腹板存在损伤时不同激励方式作用下，腹板与翼板的接收情况。从图中比较可知，对于腹板的损伤，在腹板反对称激励与腹板接收条件下识别情况最为理想。(c)与(d)是翼板存在损伤时不同激励方式作用下，腹板与翼板的接收情况。从图中可知，对于翼板的损伤，在翼板一侧激励(与损伤同一侧)与翼板一侧接收的条件下识别情况最为理想。

综合比较腹板与翼板的损伤情况可知：腹板反对称激励与翼板一侧激励的两种激励方式效果比较好；而腹板对称激励、腹板单侧激励以及翼板中间激励效果均较差；同时对于激励、损伤和接收在同一板面上(即导波的传播路径不经过腹板与翼板的交界面)的情况下识别情况最好。因此，可以以腹板与翼板交界处为分割面，将H型钢分割成5个小窄板分别进行损伤识别，即1块腹板与4小块翼板。

3.2 实验算例

在仿真的基础上，进行实验验证，实验现场如图9所示。由型号为TEK AFG3022B的信号发生器产生激励信号，将该信号分成两路：一路直接连接示波器以作参考信号，用来判断零时刻；另一路经过型号为KH-7602M的功率放大器将信号幅值放大，再通过PZT晶片将电信号转换为机械信号，在检测结构中产生导波，由PZT晶片将机械信号转换为电信号。通过型号为 DPO 3014 的示波器显示、平均化处理，保存导波响应波信号，以供后期信号处理，实现损伤的识别与定位。

仿真所得到的导波响应信号，无背景噪声，可通过求取波包的包络线获取不同模式、不同传感路径的导波的传递情况。实际实验中，由于受电磁干扰、背景噪声、传感器与作动器的安装误差等方面影响，使得实验所得的导波响应信号与仿真信号存在一定差异。使用示波器内嵌的多次平均功能，多次采样后平均处理，减小随机噪声的影响，最后通过小波变换重构采集的信号进行分析。

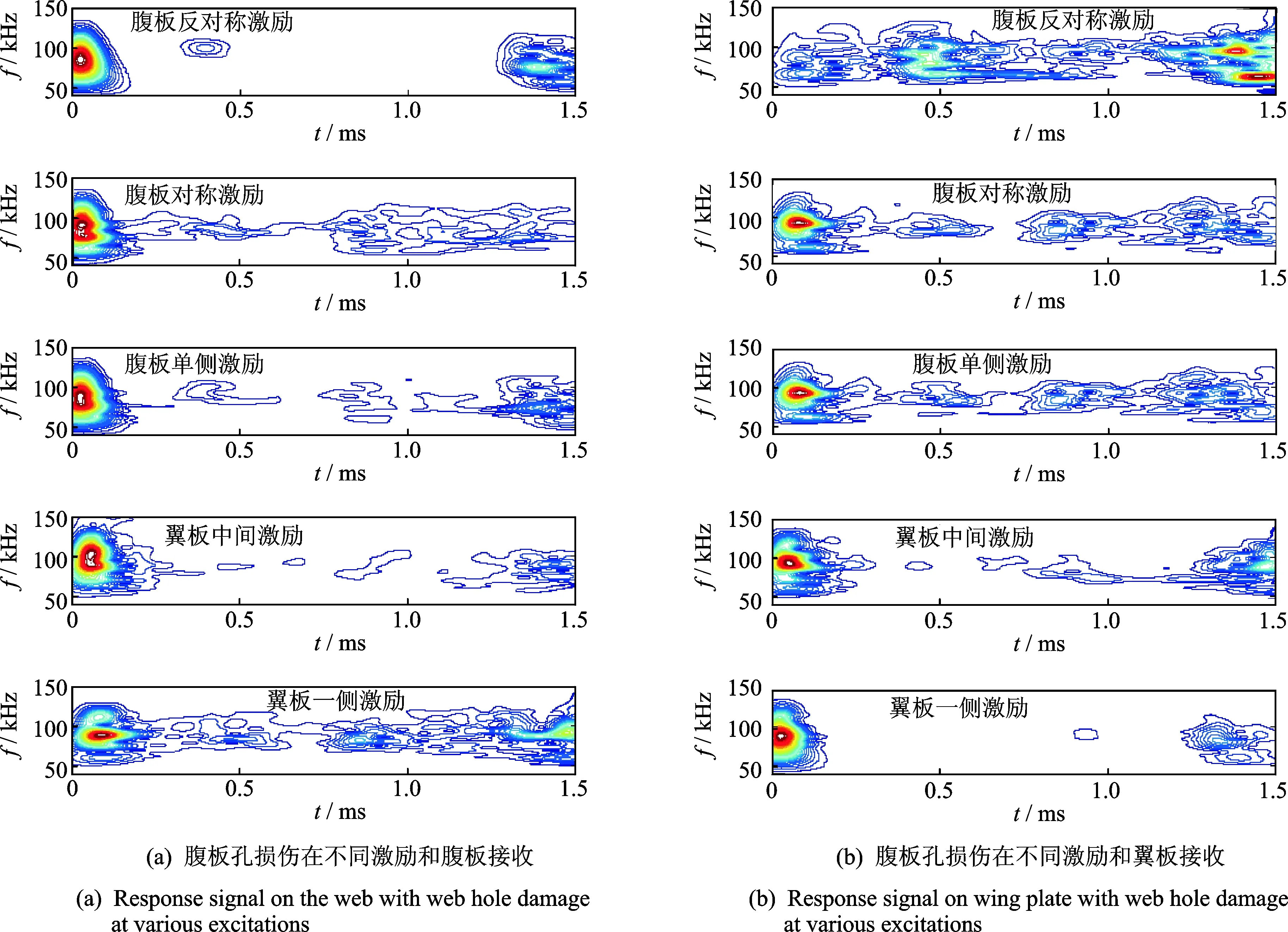
图8 不同激励与接收对损伤识别情况Fig.8 Identification ability under different excitation and receive

图9 实验现场Fig.9 Experimental environment

图10 作动器和传感器布局Fig.10 The layout of Actuator and sensor layout

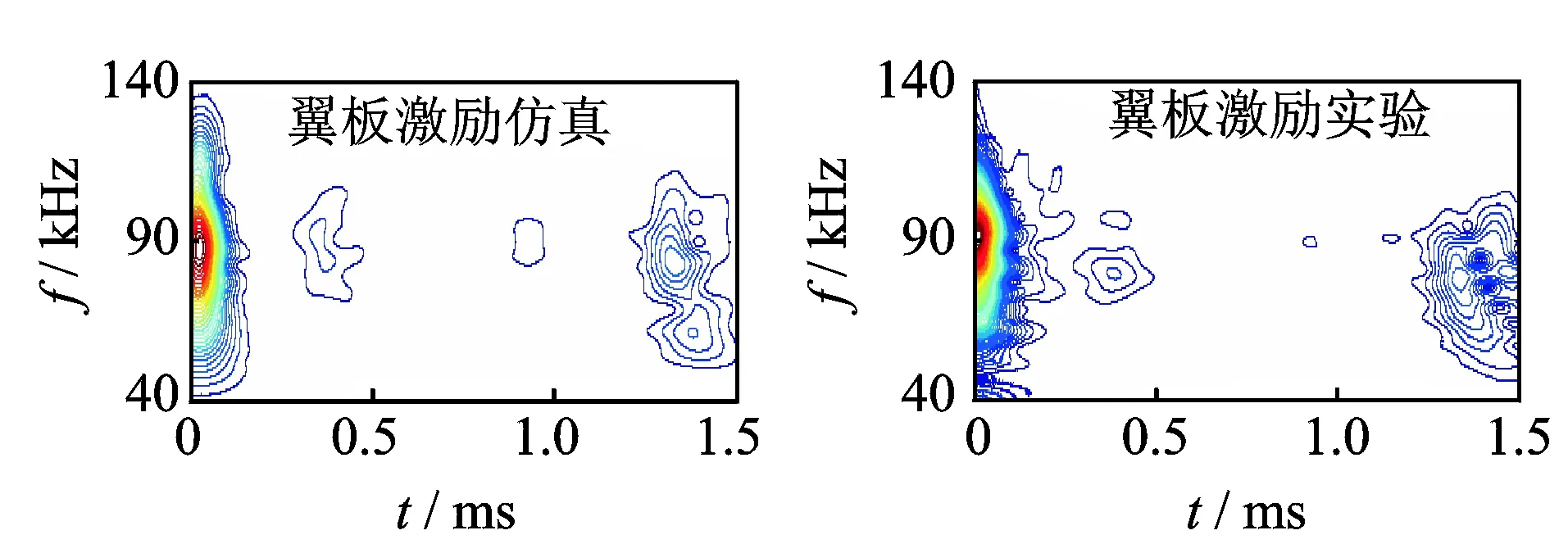
图11 相同翼板孔损伤下仿真与实验对比Fig.11 Experimental compare with the simulation result

布置如图10所示的传感网络，通过作动器A1和A2对实验工件进行激励，通过3个传感器进行数据采集，取各传感器采集信号的512组平均值经过小波变换重构。在与仿真相同位置的翼板处加工一个孔损伤，进行如图 9所示实验，同样取各传感器采集信号的512组平均值经过小波变换重构。将传感器S2的损伤信号与仿真的数据进行比较，由图11可知，实验数据与仿真数据在时间上吻合比较好，频率上由于实验过程中存在外界环境的干扰存在一定差异，但是该差异较小，不影响实验结果。

用同样的实验方法，对腹板孔损伤进行识别能力实验。在H型钢腹板进行反对称激励并用传感器进行导波信号接收。分别选取腹板存在直径为2，4，8 mm的孔损伤H型钢与无损伤的进行实验比较。导波信号如图12所示。

图12中，直径8 mm的孔损伤可以明显地识别出来，而直径为2，4 mm的孔损伤未能被识别。因此考虑对损伤信号与无损伤信号进行作差比较，提高识别度。在图13中，直径4 mm的孔损伤也可以明显地识别出来。

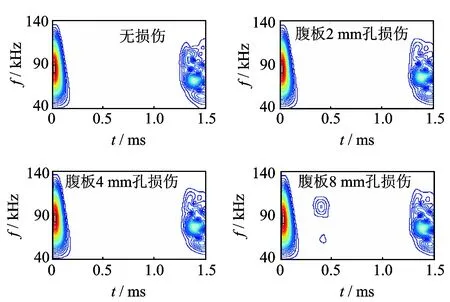
图12 腹板孔损伤的识别情况Fig.12 Web′s hole-damage identification ability

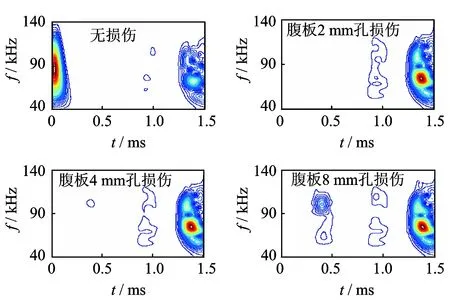
图13 腹板孔损伤的差信号Fig.13 Difference signals of the web′s Hole-Damage

4 结论

1) 以H型钢为例进行损伤定位研究。可参照Lamb波传播机理，综合导波模式、波包时域分辨率及波的结构等因素选择频率。本研究中，选用87.5 kHz的激励信号，采用Lamb波A0模式进行检测。

2) 对比A0与S0模式进行检测情况，可知A0对损伤比较敏感，所以在微损伤识别能力上强于S0模式。

3) 经过有限元仿真，采用腹板反对称激励、翼板一侧激励，将H型钢分割成5个小窄板分别进行损伤识别，能够较准确地实现H型钢的损伤定位。

4) 对于损伤信号进行作差处理，可以提高识别能力。对于本研究的H型钢，在作差的条件下可以识别出直径4 mm的孔损伤。

[1] Raghavan A, Cesnik C E S. Review of guided-wave structural health monitoring[J]. Shock and Vibration Digest, 2007, 39(2): 91-116.

[2] 陆希,孟光,李富才. 基于Lamb波的薄壁槽状结构损伤检测研究[J]. 振动与冲击,2012,12:63-67.

Lu Xi, Meng Guang, Li Fucai. Lamb wave-based damage detection for a channel-like thin-wall structure[J]. Journal of Vibration and Shock, 2012,12:63-67.(in Chinese)

[3] 孙凯, 孟光, 叶林, 等. 基于超声导波的钢梁结构损伤大小识别研究[J]. 振动与冲击, 2011, 30(9): 227-231.

Sun Kai, Meng Guang, Ye Lin, et al. Damage size identification of thick steel beam based on ultrasonic guided wave[J]. Journal of Vibration and Shock, 2011, 30(9): 227-231. (in Chinese)

[4] Alleyne D N, Cawley P. The interaction of Lamb waves with defects[J]. Ultrasonics, Ferroelectrics and Frequency Control, IEEE Transactions on, 1992, 39(3): 381-397.

[5] Alleyne D N, Cawley P. Optimization of Lamb wave inspection techniques[J]. NDT & E International, 1992, 25(1): 11-22.

[6] Lowe M J S, Cawley P, Kao J Y, et al. The low frequency reflection characteristics of the fundamental antisymmetric Lamb wave a0 from a rectangular notch in a plate[J]. The Journal of the Acoustical Society of America, 2002, 112(6): 2612-2622.

[7] Lowe M J S, Diligent O. Low-frequency reflection characteristics of the S0 Lamb wave from a rectangular notch in a plate[J]. The Journal of the Acoustical Society of America, 2002, 111(1): 64-74.

[8] Rose J L. Ultrasonic waves in solid media[M]. [S.l.]:Cambridge University Press, 2004:82-107.

[9] Bartoli I, di Scalea F L, Fateh M, et al. Modeling guided wave propagation with application to the long-range defect detection in railroad tracks[J]. NDT & E International, 2005, 38(5): 325-334.

[10] Giurgiutiu V. Tuned Lamb wave excitation and detection with piezoelectric wafer active sensors for structural health monitoring[J]. Journal of Intelligent Material Systems and Structures, 2005, 16(4): 291-305.

10.16450/j.cnki.issn.1004-6801.2017.06.022

国家自然科学基金资助项目(11372179)；教育部新世纪优秀人才资助项目(NCET-13-0363)

2015-12-13；

2016-01-19

TH113.1； TB559