基于FBG的齿根弯曲应力在线检测方法

2018-01-04王洪海李洋洋汪金铭李政颖

振动、测试与诊断 2017年6期

王洪海，李洋洋，2，徐刚，3，汪金铭，李政颖，4

(1.武汉理工大学光纤传感技术国家工程实验室武汉，430070) (2.中国长江电力股份有限公司宜昌，443000)(3.湖北工程学院机械工程系孝感，432000)(4.武汉理工大学光纤传感技术与信息处理教育部重点实验室武汉，430070)

基于FBG的齿根弯曲应力在线检测方法

王洪海1，李洋洋1，2，徐刚1，3，汪金铭1，李政颖1，4

根据国际标准化组织(international organization for standardization, 简称ISO)和美国齿轮制造者协会(American gear manufacturers association,简称AGMA)关于渐开线圆柱齿轮强度的计算方法，在计算单个齿轮齿根弯曲应力时，可将轮齿简化为一悬臂梁。基于此，提出了一种齿根弯曲应力在线检测的新方法，利用光纤布拉格光栅(fiber Bragg grating，简称FBG)的应变特性和齿轮传递扭矩时轮齿产生的挠度，将齿根弯曲应力的测量转化为光栅反射波长的测量，通过对反射波长的实时解调，能够实现对运行中齿轮的齿根弯曲应力进行实时在线检测。通过对一对渐开线圆柱尼龙斜齿轮进行分析，并在1～18 N·m扭矩范围进行实验，结果表明该方法能够准确测量齿根的弯曲应力，灵敏度高达70 pm/MPa，线性拟合度达0.99以上，且响应速度快。利用光纤光栅准确检测齿轮运行时的齿根弯曲应力，不但能够代入实际工况实现在线检测，同时对齿轮的设计和故障诊断具有指导意义。

齿轮; 弯曲应力; 光纤光栅; 在线检测

引言

随着齿轮的不断发展和应用场合的更加严苛，对齿轮的强度分析提出了更加精确的要求，尤其是针对运行状态的齿轮系。关于渐开线齿轮齿根弯曲应力的计算方法和测量方法，各国学者都进行了深入的研究，同时也颁布了许多相应的标准，当前使用比较广泛的基础标准主要是ISO和AGMA标准[1]，二者的共同之处是均将单个轮齿视为悬臂梁进行求解，因为在轮齿弹性范围内将其近似为悬臂梁并不会产生很大误差。

目前，国内外许多学者提出了多种方法对齿根弯曲应力进行研究[2-6]，主要包括理论分析和实际测量两种方法。理论分析方法主要包括公式的推导优化和三维的仿真分析两种。公式推导优化虽然能够从理论上针对各种工况进行参数上的修正，但各个参数的选择大多只能依靠经验进行，不能把传动时的实际工况考虑进来，导致了结果的差异性；三维仿真分析是近些年使用比较多的方法之一，主要是通过建模软件建立三维模型，然后导入Ansys等分析软件进行力学分析。三维仿真相对公式推导而言更加接近实际情况，但由于边界条件仍难以与实际工况完全相符，导致仿真结果与真实值存在一定的出入[7]。目前，实际测量方法主要是采用粘贴应变片的方法，应变片测量的方法虽然能够代入工况进行实际测量，但是应变片的组桥方式较为复杂，动态信号不易采集，且齿根处的粘贴空间较为狭小，实际操作中大多需要对轮齿进行二次加工。经过再加工的齿轮使用时必然会在加工处出现应力集中现象，不但会影响到测量结果的准确性，还降低了齿轮的使用寿命，严重时甚至会发生安全事故，故应变片多用于静态的测量和标定。因此，对于高速、狭小的齿轮系统，急需一种新的齿根弯曲应力检测方法。

近些年来，光纤光栅传感技术取得了突飞猛进的发展[8]，光纤光栅凭借其体积小、成本低、灵敏度高及抗电磁干扰等优势，目前已成为最具代表性、最有发展前途的传感器之一。随着研究的不断深入，光纤光栅传感技术应用场合愈来愈广泛，测量更是涉及到温度[9]、燃气泄漏[10]、应变[11]及振动[12]等各个领域内，不论是在实验室还是在实际使用中均取得了良好的效果。同样，将光纤光栅用于应力测量和状态检测的案例不胜枚举，例如：兰玉文等[13]设计了一种光纤光栅三维应力传感器，能够准确测量三维空间任意方向的应力；祁耀斌等[14]使用光纤光栅传感技术成功对海上浮吊吊臂桁架结构进行了健康监测。

齿轮在啮合传动时，齿轮之间扭矩的传递是通过轮齿之间的相互作用进行的，在传递扭矩的同时齿根处会产生弯曲应力，轮齿相对于齿根位置会产生一定的挠度。考虑到对挠度的测量比直接对应力进行测量要更加容易，而且光纤光栅在测量微小应变时可以极大地发挥其独特的优势，笔者基于光纤光栅传感技术和齿轮理论分析，提出了一种新型齿根弯曲应力在线检测方法，设计了一种光纤光栅在齿轮上的布置方法和信号采集装置，并通过对一对相互啮合的渐开线塑料斜齿轮进行实验研究来验证本方法的准确性。

1 齿根弯曲应力的光纤光栅测量方法

1.1 齿根弯曲应力的计算模型

图1所示为一长度为l的悬臂梁在端部受单个载荷F作用下的变形简图，以沿梁的长度方向为坐标轴，根据材料力学相关知识，其挠曲线方程为

(1)

其中：E为材料的弹性模量；I为对中性轴的惯性矩；EI合称为梁的抗弯刚度；a为载荷作用点距离固定端的距离；x为任意点距离固定端的距离。

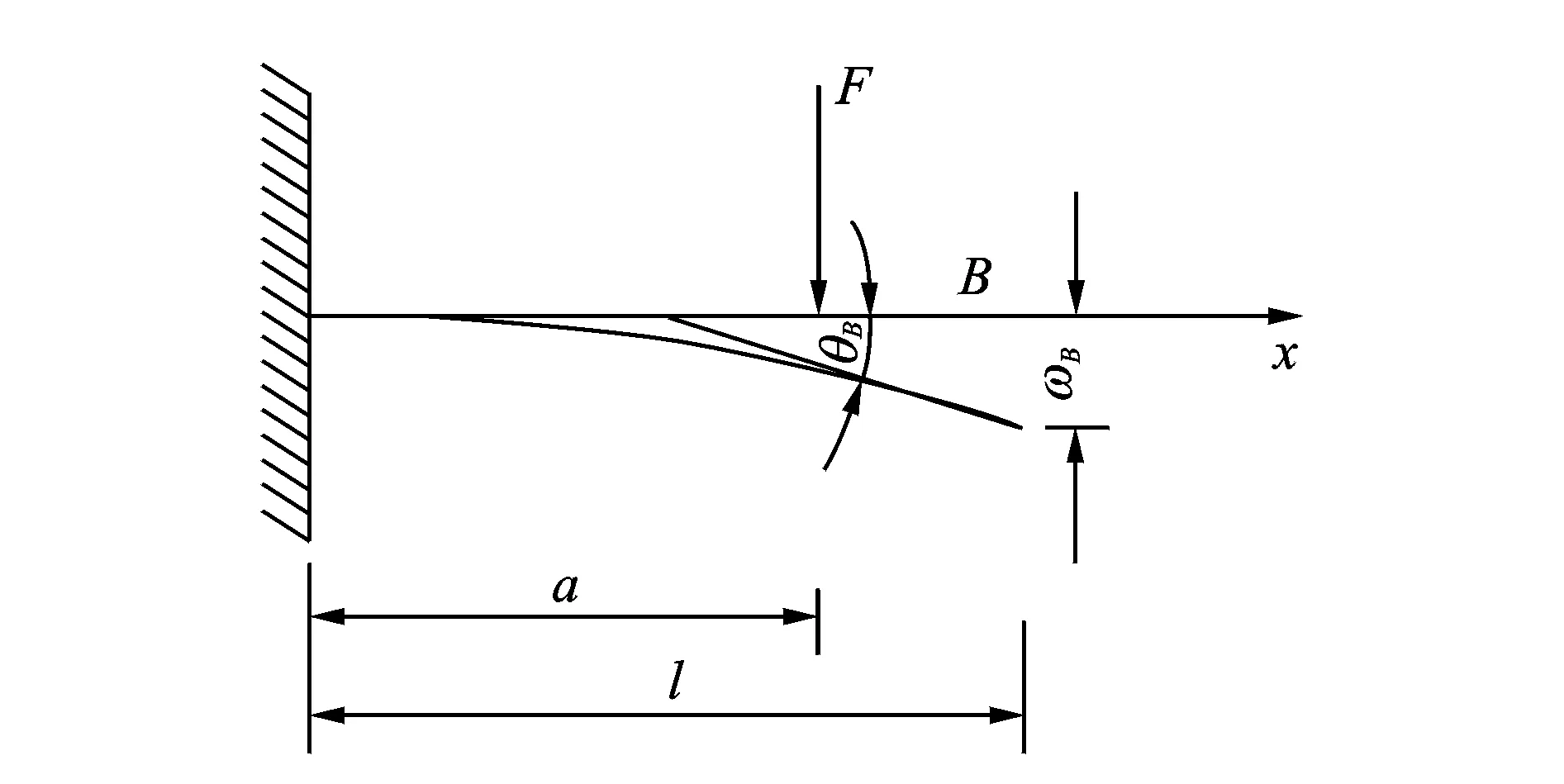
图1 悬臂梁受力分析Fig.1 Force analysis of cantilever beams

由式(1)能够看出，当施加的单个载荷F作用的位置固定后，则在某一固定位置由该载荷作用所产生的挠度ω只跟载荷F的大小有关，且二者成线性关系。由此考虑，若将齿轮轮齿视作悬臂梁，当齿轮受到载荷的作用时，将会沿圆周方向产生很小的挠度，如图2所示，该挠度将会与齿轮所受的圆周力成线性关系。

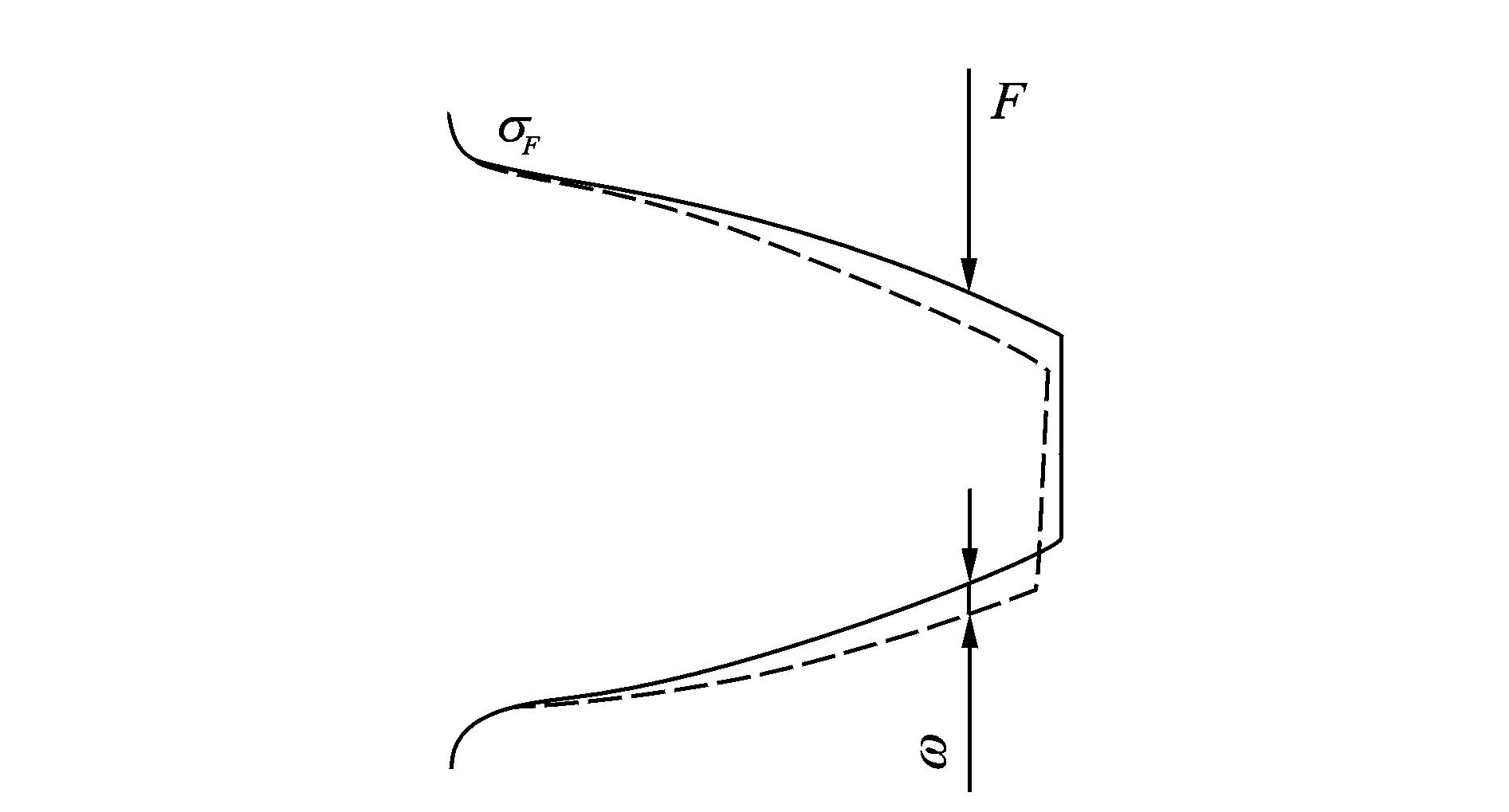
图2 轮齿变形示意图Fig.2 Schematic diagram of gear tooth deformation

在斜齿轮传动中，齿轮受力分析如图3所示。作用在齿面上的法向载荷Fn垂直于齿面，该载荷与节圆柱的切面Pa′bc倾斜成一角度，称为法向啮合角αn。法向力Fn可分解为3个相互垂直的分力，分别为沿齿轮周向的力Ft、沿齿轮径向的力Fr以及沿轴向的力Fa，3个分力的方向如图3所示。由机械设计相关知识，斜齿轮轮齿的弯曲应力公式为

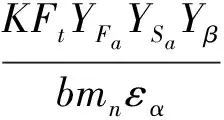
(2)

其中：K为载荷系数；YFa为齿轮的齿形系数；YSa为应力校正系数；Yβ为螺旋角影响系数；b为齿宽；mn为法向模数；εα为端面重合度。

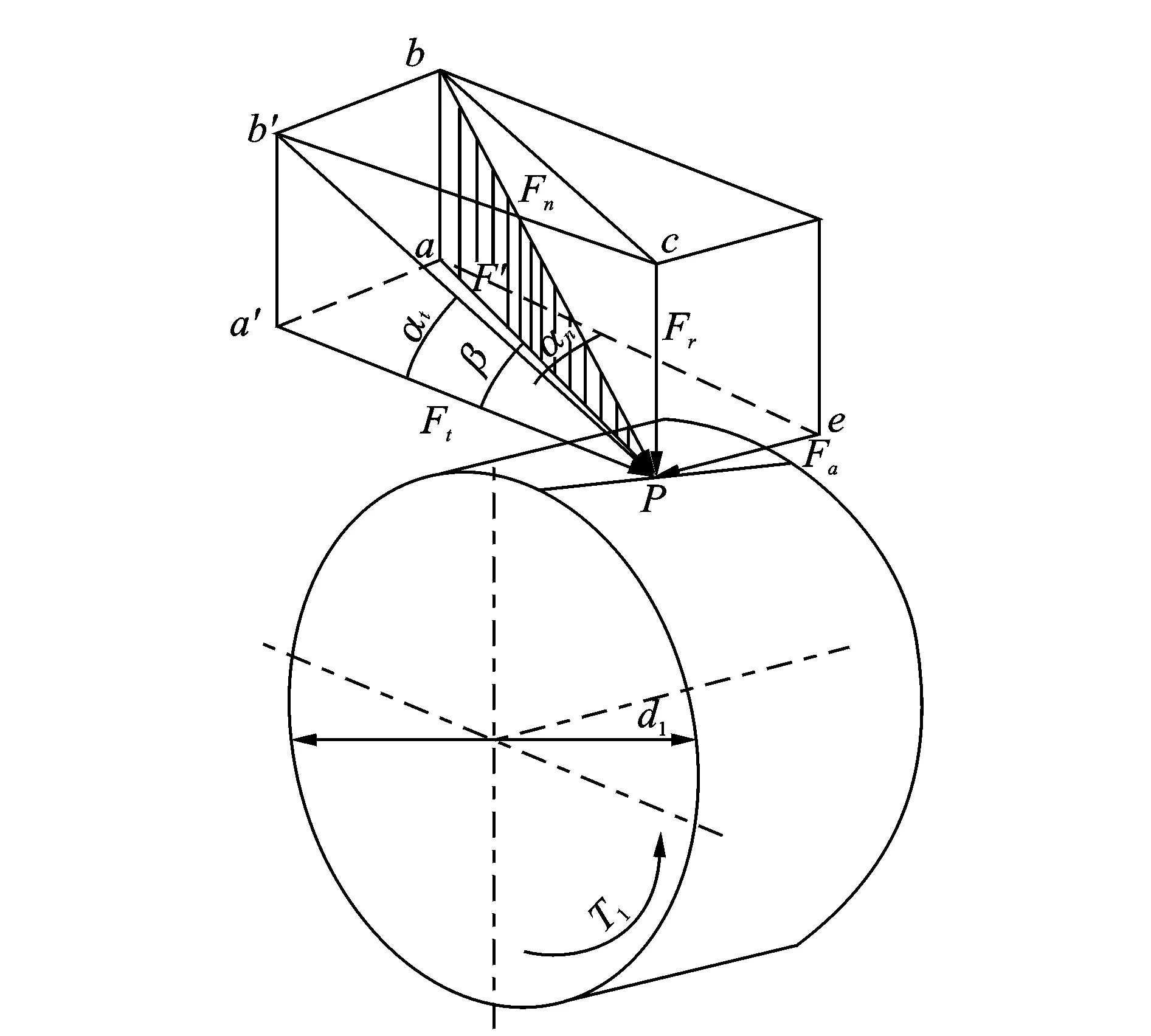
图3 齿轮受力分析Fig.3 Force analysis of gear

以上各个系数中，除了Ft随着传动的扭矩发生变化之外，其余都可通过齿轮参数进行计算或者查阅相关手册得到，并且当齿轮型号选定且不改变相互配合的情况下，则齿根的弯曲应力随着Ft单调变化且呈线性关系，进而跟齿轮所产生的挠度即应变同样呈线性关系，这就从理论上保证了光纤光栅测量弯曲应力会有很好的线性输出。

1.2 光纤光栅测量应变的基本原理

用一束宽带光谱注入到光纤布拉格光栅，则其会反射回来一束窄带光波，反射回来的光波的中心波长称之为布拉格波长，由光纤耦合模理论可知其数学表达式为

λB=2neffΛ

(3)

其中：Λ为光栅的栅格周期；neff为光纤纤芯的有效折射率。

当光纤布拉格光栅受到轴向外界力的作用时，光栅周期Λ会产生ΔΛ的变化，同时由于光弹效应会导致光栅的有效折射率neff发生Δneff的变化，二者的变化会导致反射光波的波长λB发生ΔλB的偏移。将式(3)进行微分并忽略高阶无穷小后得到

ΔλB=2ΔneffΛ+2neffΔΛ

(4)

将以上两式相比得到

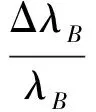
(5)

在光栅的弹性范围内有

ε=ΔΛ/Λ

(6)

其中：ε为光栅的轴向应变。

当光栅只受到轴向力的作用，由轴向变形引起的弹光效应所带来的折射率变化为

Δneff/neff=-Pε

(7)

其中：P为一个跟折射率、弹光常数和材料泊松比有关的系数，当光纤光栅的材料确定后，P可视作一常数。

将式(6)和式(7)代入到式(5)中有

ΔλB/λB=(1-P)ε

(8)

由式(8)能够看出，光纤光栅的反射波长变化与光纤光栅的轴向应变呈线性关系，因而可以通过解调反射的布拉格波长反演出光纤光栅的轴向应变。

2 实验方案设计

2.1 实验装置

实验以一对相互啮合的渐开线圆柱斜齿轮为研究对象，齿轮参数和材料属性如表1和表2所示。

表1 齿轮的基本参数

表2 齿轮材料属性

实验以变频电机为驱动原件带动齿轮对传动，电机受变频器控制可对其转速进行调谐；以磁粉制动器为负载装置，利用张力控制器可对其施加的扭矩加以控制；使用光纤滑环连接器作为光栅信号的传输中介，利用其相对转速高的原理，实现信号由高速旋转轴到静态解调仪的传输；利用扭矩转速传感器采集扭矩和转速的信号，便于后续分析。实验装置简图和实物图分别如图4和图5所示。

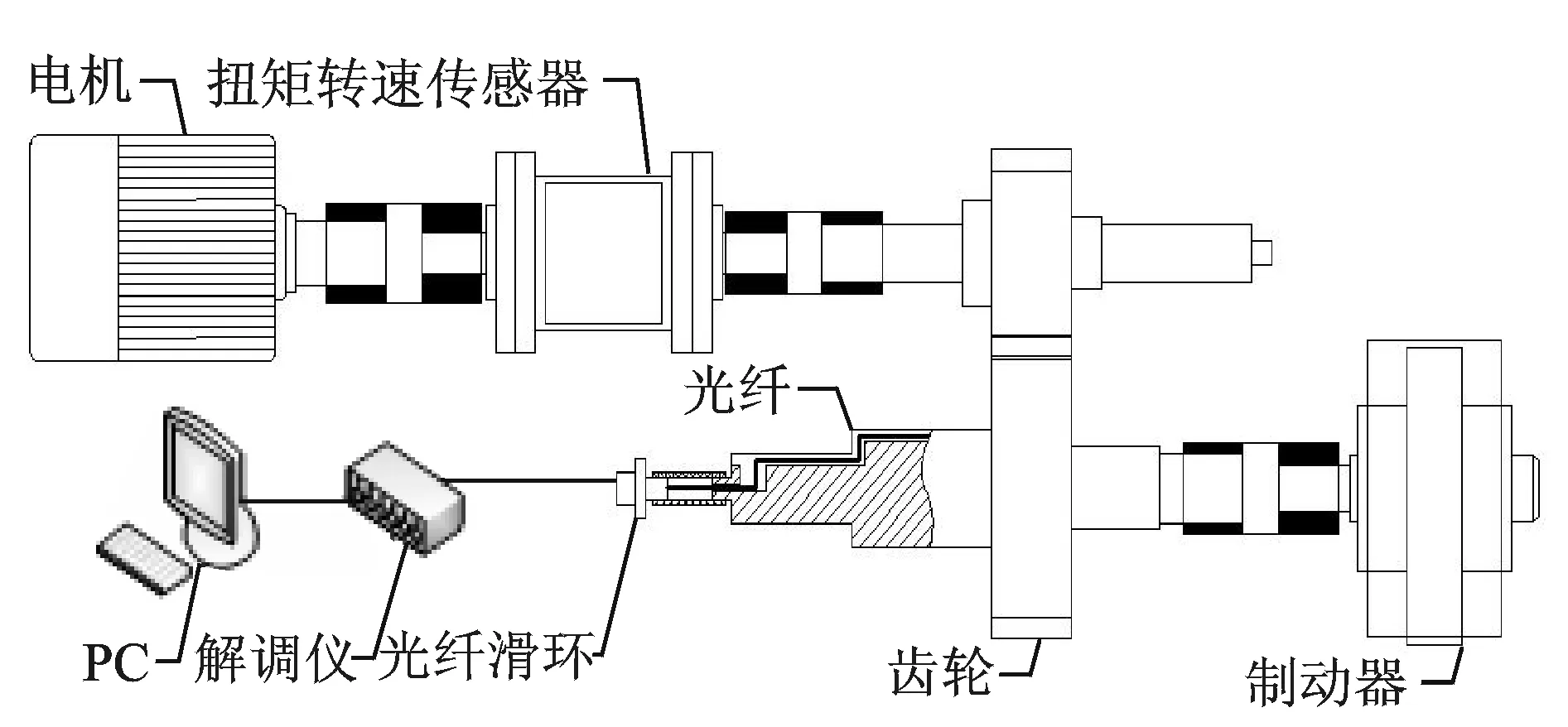
图4 实验系统示意图Fig.4 Schematic diagram of experimental system

图5 实验台实物图Fig.5 Picture of test-bed

2.2 光纤光栅和应变片的粘贴方法

根据光纤光栅传感检测的原理，光纤光栅只能感受轴线方向的应变，因此需要合理布置光纤光栅的位置，使轮齿所发生的挠度能够转化为光纤光栅轴线方向的应变。实验中所采用的光纤光栅和应变片的布置方法如图6所示。通过将光纤粘贴在两相邻轮齿的齿侧，保证测量光栅处在两轮齿之间，根据材料力学知识，轮齿在受力发生偏移的时候，由于挠度相对轮齿高足够小，故在轮齿弹性范围内可看作应变是沿着光栅轴线方向，并且由此所引起的误差是在所允许的范围之内。由式(1)分析可知，越靠近齿顶的地方发生的挠度越大，因而光栅的位置越靠近齿顶，波长的漂移量越大，灵敏度越高，对光栅的预拉伸量要求就越高，对误差的放大也就越明显。综合考虑以上因素并进行相关实验分析，本实验选择距离齿根5 mm处的位置进行光栅的粘贴测量，光栅长度为4 mm。

与此同时，在轮齿的齿根处粘贴测量应变片，参考应变片粘贴在齿侧处。通过应变片组成电桥测量不同转矩下的齿根弯曲应力，通过光栅测量对应的波长漂移，进行波长漂移和齿根弯曲应力之间的标定。由于齿根空间狭小，故选用敏感栅尺寸为1.0 mm×2.0 mm的箔式电阻应变片进行弯曲应力的测量。应变片体积相对齿根安全区域极小，故应变片的应变可完全视为齿根应力所引起的，使用电阻应变仪的分辨率能够达到0.1 με，其对应的波长漂移为0.122 pm，高于解调仪的精度；因此，使用应变片进行光栅标定不会损失精度。

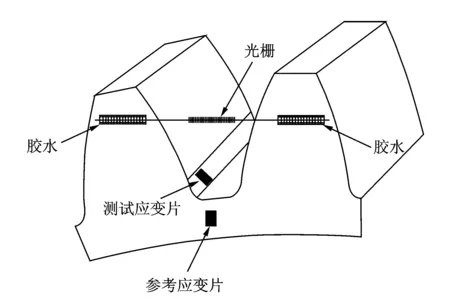
图6 光纤光栅和应变片粘贴示意图Fig.6 Paste of fiber Bragg grating

3 实验结果分析

3.1 静态下的实验结果

实验分别在6种不同扭矩下，采用应变片和光纤光栅同时测量齿轮在不发生转动的极限弯曲应力和与其对应的波长漂移量，并根据式(2)计算得到弯曲应力的理论值，结果如表3所示。绘制波长增量随应变片测得的弯曲应力的变化曲线如图7所示，不同转矩下应变片测得弯曲应力和理论计算弯曲应力关系如图8所示。

表3静态时不同扭矩下的弯曲应力与波长增量

Tab.3Bendingstressandwavelengthincrementunderdifferentstatictorque

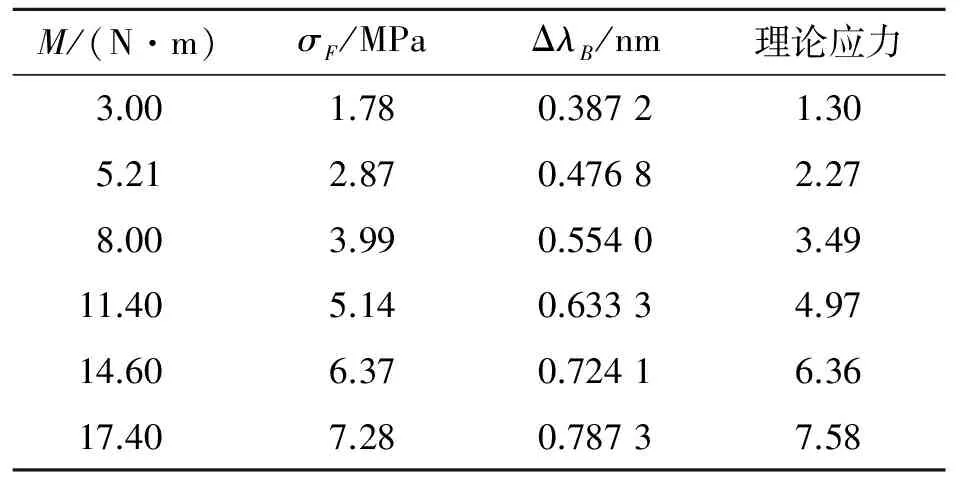
M/(N·m)σF/MPaΔλB/nm理论应力3．001．780．38721．305．212．870．47682．278．003．990．55403．4911．405．140．63334．9714．606．370．72416．3617．407．280．78737．58

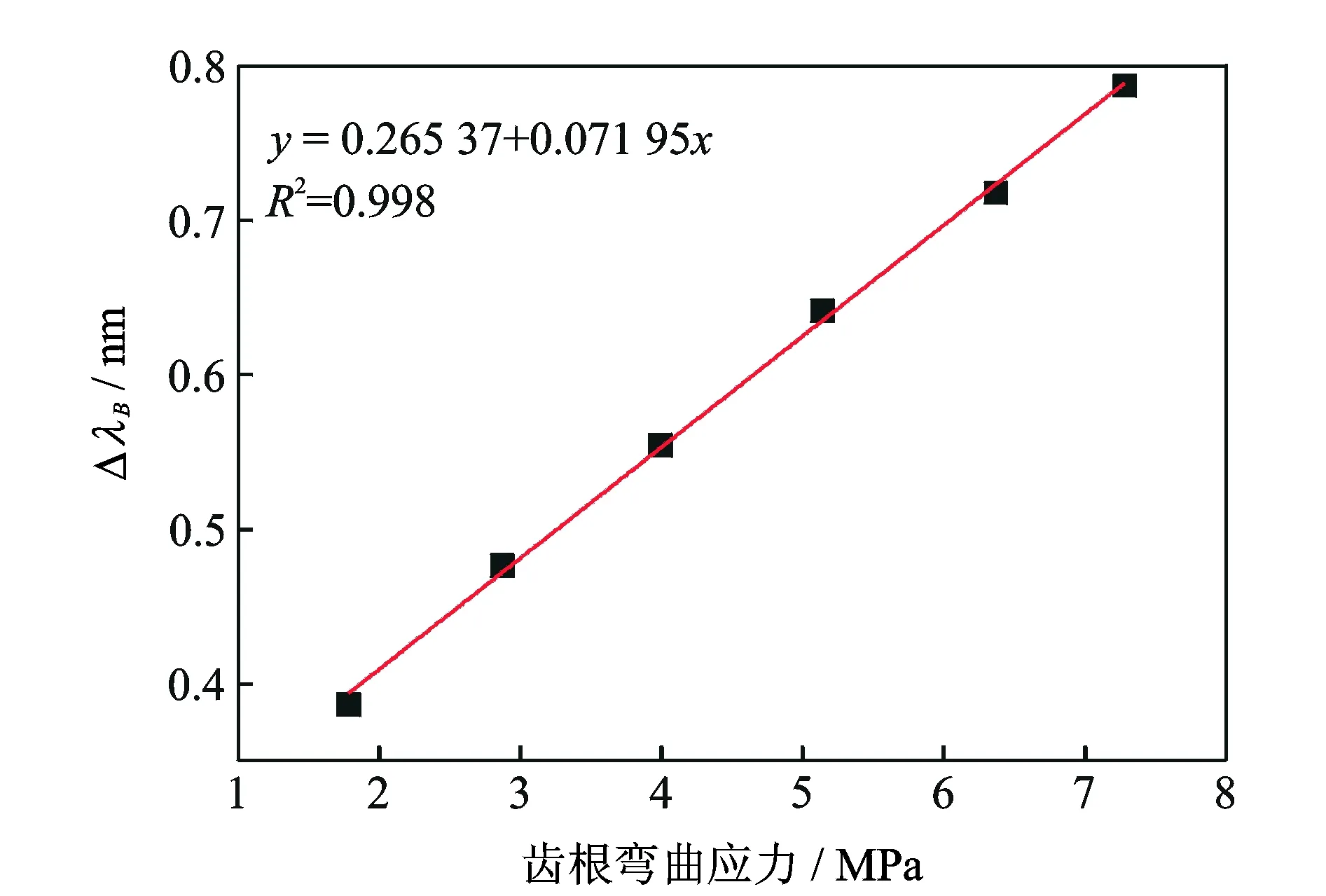
图7 静态时ΔλB-σF图Fig.7 ΔλB-σF in static state

图8 应变片测得弯曲应力和理论值的关系Fig.8 The relationship of bending stress between the strain gauge and the theoretical stress

由图7可知，在不同的扭矩下波长增量与齿根弯曲应力变化趋势一致，且二者呈线性变化，线性拟合度达到0.998。由图8可以看出，使用应变片测得弯曲应力值和理论计算值相差不大，用来标定光栅不会产生很大误差。静态下的实验结果表明，通过这种方式粘贴的光纤光栅在测量齿根处的弯曲应力时有良好的线性输出。

3.2 动态测量的实验结果

图9(a)为光纤光栅在转速为500 r/min时连续采集的几个周期的信号。由图中可以看到，在一个啮合周期内，光纤光栅呈现先被拉伸之后又被压缩的状态。这是由于当粘贴光栅的第1个轮齿进入啮合区时，由于圆周力的原因对光栅有沿轴线拉伸的作用；当粘贴光栅的第2个轮齿也进入啮合区时，由于会受到相同方向的圆周力，该圆周力使光栅沿轴向方向压缩，所以会减弱对光栅的拉伸；随着啮合的深入，第1个轮齿渐渐退出啮合区，光栅就从拉伸状态转为压缩状态。由图中可以看到信号周期为0.18 s，取图中的ΔλB为光栅波长漂移量，由于外界温度等噪声信号的影响，只会是波长图整体上下漂移，结果取ΔλB进行分析已经消除了由于温度带来的影响，故无需做温度补偿。图9(b)为对上述信号进行傅里叶变换之后的频谱图，可以看到信号主要成分为频率为5.56 Hz及其倍频分量。根据主动轮转速为500 r/min，传动比为3∶2，所计算出来从动轮的啮合周期为0.18 s，频率为5.56 Hz，与得到的信号相吻合，说明该方法可以准确采集到运行状态下的齿根弯曲应力。

实验测量了在3种不同转速、6种不同扭矩下反射波长的变化情况，如图 10 所示。根据静态时所标定函数关系进行弯曲应力的换算，得到每个转矩对应下的弯曲应力值，结果如表4所示。根据弯曲应力随扭矩的变化关系所拟合出的曲线如图11所示。

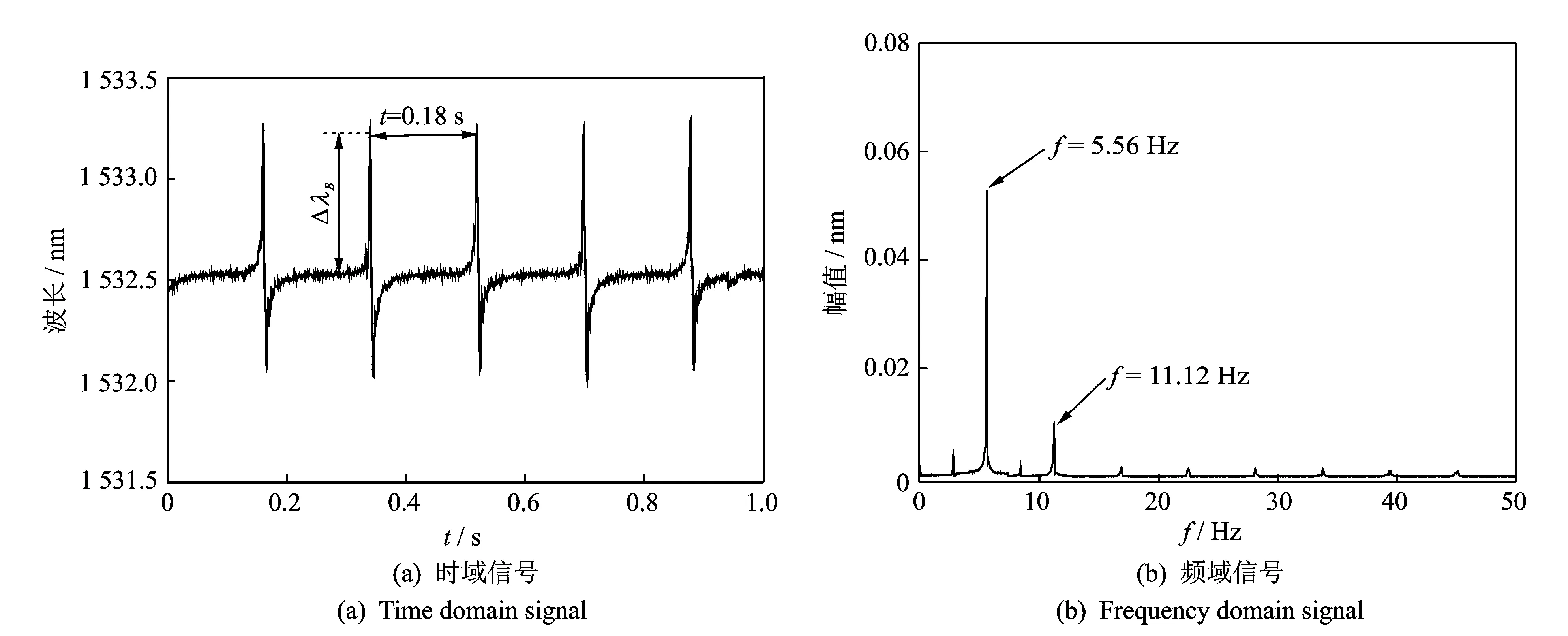
图9 光纤光栅应变信号Fig.9 Fiber Bragg grating strain signal

表4不同工况下测得的弯曲应力

Tab.4DetectionofbendingstressunderdifferentworkingconditionsMPa

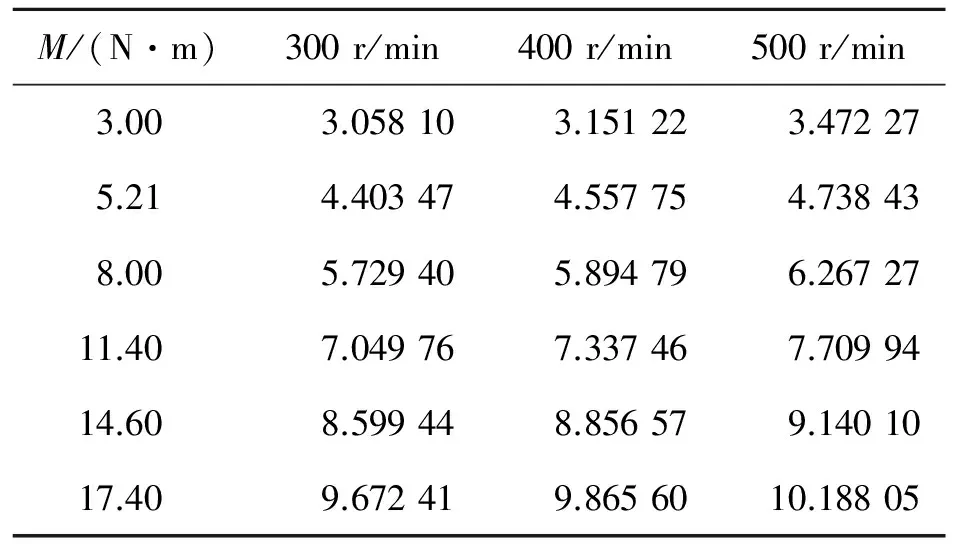
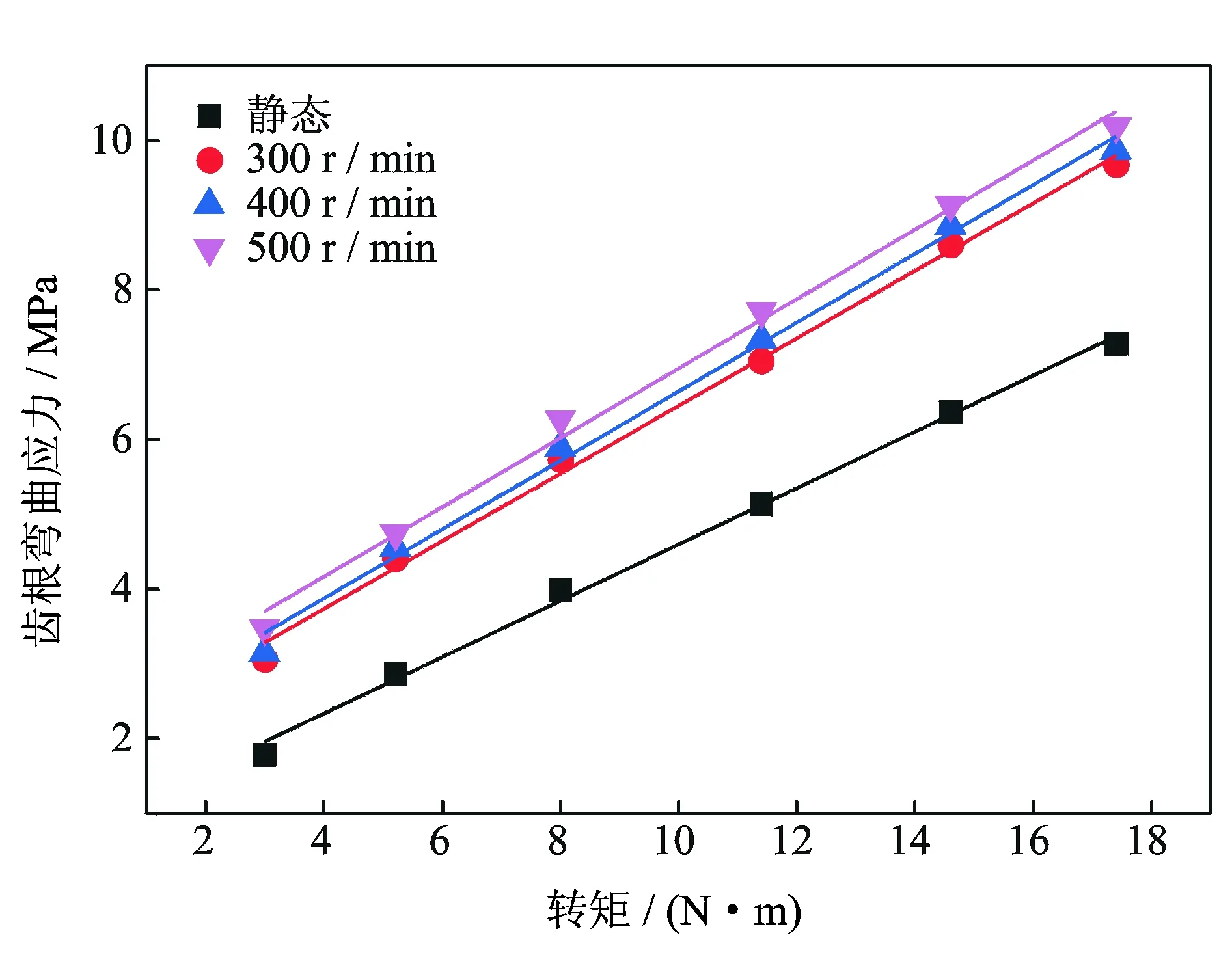
图11 不同扭矩下测得的弯曲应力Fig.11 Detection of bending stress under different working conditions

由图10可以看到，齿轮在啮合时，随着转速的提高，相同时间内出现的啮合次数随之增加；随着齿轮传递转矩的增大，轮齿所受力越大，挠度越大，对光栅产生的轴向应变就越明显，反射波长变化就越大。由图11可以看到，随着齿轮传递扭矩的增加，光纤光栅所测得的弯曲应力也随之增加，且二者呈良好的线性关系，线性拟合度因子均达到0.99以上，所以波长变化能够很好地表征齿根的弯曲应力。针对本实验中的塑料斜齿轮和光栅粘贴的位置，灵敏度在70 pm/MPa以上。由于使用系数KA和动载荷系数KV的原因，在同一扭矩下，动态弯曲应力比静态弯曲应力要大，就测得弯曲应力而言，二者的比值在1.2～1.4之间，且随着转速的增大，该比值也在增加。由机械手册查得，在该工况下KAKV的乘积在1.4以上，说明使用理论公式计算的弯曲应力是偏于保守的。

4 结束语

本研究从计算轮齿弯曲应力时可将其视作悬臂梁模型的理论出发，结合FBG传感的独特优势，提出了一种在线检测齿根弯曲应力的新方法。针对不同的转速和扭矩分别进行了多次实验，结果证明该方法能够有效地针对正常运行中的齿轮进行齿根弯曲应力的在线检测，且线性度好，灵敏度高，效果理想。该方法克服了传统方法弊端，能够把实际工况代入进行测量，结果更加真实可靠。

[1] 吴昌林,吕云霏.ISO与AGMA渐开线圆柱齿轮强度计算标准的比较[J].中国机械工程, 2011,12:1418-1423,1465.

Wu Changlin，Lü Yunfei. Comparison between ISO and AGMA gear strength rating methods for involute cylindrical gears[J].China Mechanical Engineering, 2011,12:1418-1423,1465. (in Chinese)

[2] Wang Yao, Lin Chao, Cai Zhiqin, et al. Bending stress analysis of orthogonal curve-face gear[J]. Journal of Advanced Mechanical Design, Systems and Manufacturing, 2016, 10：15.

[3] Deng Song, Hua Lin, Han Xinghui, et al. Finite element analysis of contact fatigue and bending fatigue of a theoretical assembling straight bevel gear pair[J]. Journal of Central South University, 2013(2):279-292.

[4] Zhao Xindan, Niu Hang, Zhang Xiaodong. Research on measurement for bending stress of gear with fiber Bragg grating (FBG) and optimization of FBG probe installation[C]∥International Conference on Ubiquitous Robots and Ambient Intelligence. Goyang, South Korea: IEEE, 2015:336-340.

[5] Pedersen N L. Minimizing tooth bending stress in spur gears with simplified shapes of fillet and tool shape determination[J]. Engineering Optimization, 2015,47(3):805-824.

[6] 彭玉海,侯红玲,王长乾,等.齿轮齿根弯曲疲劳耐久性测试方法及测试装置：中国，CN104266836A[P]. 2015-01-07.

[7] 李晗,谭跃刚,蒋熙馨,等.基于光纤光栅的直齿圆柱齿轮应力修正系数优化[J].机械工程师,2015,10:142-146.

Li Han, Tan Yuegang, Jiang Xixin, et al.Stress concentration factor optimization of spur gear based on FBG strain measurement[J]. Mechanical Engineer, 2015,10:142-146. (in Chinese)

[8] 张小栋,谢思莹,牛杭,等.光纤动态检测技术的研究与进展[J]. 振动、测试与诊断, 2015,35(3): 409-416.

Zhang Xiaodong, Xie Siying, Niu Hang, et al. Research on dynamic measurement technology of fiber optic sensors and their development[J]. Journal of Vibration， Measurement & Diagnosis, 2015,35(3):409-416. (in Chinese)

[9] Sugino M, Ogata M, Mizuno K, et al. Development of zinc coating methods on fiber bragg grating temperature sensors[J]. IEEE Transactions on Applied Superconductivity, 2016, 26(3):1-9.

[10] 任亮,夏梦颖,姜涛,等. 基于环向应变的燃气管道泄漏监测试验[J]. 振动、测试与诊断, 2015,35(5):820- 825.

Ren Liang, Xia Mengyin, Jiang Tao, et al. Leakage detection of gas pipeline based on hoop strain monitoring [J]. Journal of Vibration,Measurement & Diagnosis, 2015, 35(5):820-825. (in Chinese)

[11] Li Kuo, Zhou Zhen′an. A high sensitive fiber Bragg grating strain sensor with automatic temperature compensation[J]. Chinese Optics Letters, 2009(3):191-193.

[12] 李琳,付世晓,杨建民.运用光纤光栅传感器的涡激振动测试技术[J].振动、测试与诊断,2011,31(6):728-732.

Li Lin, Fu Shixiao, Yang Jianmin. Measuring technique based on the fiber bragg used in the vortex-induced- vibration model test[J]. Journal of Vibration,Measurement & Diagnosis, 2011,31(6):728-732. (in Chinese)

[13] 兰玉文,刘波,罗建花.光纤光栅三维应力传感器的设计与实现[J].光子学报,2009(3):656-659.

Lan Yuwen, Liu Bo, Luo Jianhua. Design and realization of three dimensional stress sensor of fiber Bragg grating[J]. Acta Photonica Sinica, 2009(3):656-659. (in Chinese)

[14] 祁耀斌,何进飞,梁磊.大型海上浮吊吊臂桁架结构光纤光栅实时监测系统研究[J].中南大学学报：自然科学版,2012(9):3455-3463.

Qi Yaobin, He Jinfei, Liang Lei. Fiber bragg grating real-time monitoring system of boom truss structure of large-scale offshore floating crane[J]. Journal of Central South University：Natural Science Edition,2012(9):3455-3463. (in Chinese)

10.16450/j.cnki.issn.1004-6801.2017.06.013

国家自然科学基金资助项目(61575149，61290311)

2015-12-22；

2016-04-28

TH132.41