齐射型多管火炮内弹道性能仿真

肖建光,郑元枫，郭张霞，刘宗超，高跃飞

(1.中北大学 机电工程学院， 太原 030051； 2.北京理工大学 爆炸科学与技术国家重点实验室， 北京 100081；3.内蒙古北方重工业集团有限公司，内蒙古 包头 014033)

【火炮和自动武器】

齐射型多管火炮内弹道性能仿真

肖建光1,郑元枫2，郭张霞1，刘宗超3，高跃飞1

(1.中北大学 机电工程学院， 太原 030051； 2.北京理工大学 爆炸科学与技术国家重点实验室， 北京 100081；3.内蒙古北方重工业集团有限公司，内蒙古 包头 014033)

基于经典内弹道方程组，引入新的内弹道参数-身管个数，推导了齐射型多管火炮内弹道方程组。结果表明，火药燃气由单个药室沿多个身管膨胀时，引起了内弹道基本方程的显著变化。管数的增加虽然使次要功成倍增加，但弹丸动能也相应提高，二者的比值保持不变，即齐射型多管火炮次要功系数与同口径单管火炮相等。当将齐射型多管火炮内弹道方程组用相对量表示时，它与经典内弹道方程组具有统一的形式。二者之间的区别在于常量的计算方式不同，如药室容积缩颈长l0、弹丸极限速度vj、综合参量B等。通过对常量计算公式的分析，提出了两种齐射型多管火炮内弹道计算的等效方法，即单管等效与多管等效。

掘进系统；齐射；多管火炮；内弹道仿真；等效法

钻地武器是高效毁伤地下深层目标，如地下指挥所、核设施等高价值军事目标的重要手段。随着地下目标埋藏深度的提高，钻地弹得到了迅速的发展[1-5]。从1991年海湾战争中使用的宝石路激光制导炸弹GBU-28，到“炸弹之母”GBU-43，再到“炸弹之祖”GBU-57，其发展仅仅经历了十几年的时间，对混凝土的穿透能力也由6 m提高得到了60 m。2007年3月14日，美国国防威胁降低局(DTRA)宣布成功试验了用于毁伤地下硬质目标设施的13.6吨级常规“巨型钻地弹———MOP”，也就是人们所熟知的“炸弹之祖”。它不仅能够摧毁采用混凝土加固地下60 m的目标，还具有精确打击能力，是美军现役最大的常规钻地炸弹。然而，由于“炸弹之祖”庞大的自身重量，其携载平台受到了严格的限制，目前只有B-2、B-52等型号的战略轰炸机才能满足挂载需求。因此，采用新的钻地原理实现钻地武器的小型化是当今钻地弹发展的重要方向之一。

深钻地掘进武器系统概念及技术的发展，为有效打击地下深层坚固目标提供了新的思路和途径[6]。深钻地掘进武器又叫“深度挖掘者”，其重量仅为90 kg，对混凝土的穿透能力为10 m。它对目标的打击和毁伤过程可分为两个阶段，第一阶段为掘进开坑过程，通过弹载多管火炮系统齐射多枚侵爆子弹，利用侵爆子弹的侵彻/爆破作用，将地下岩土抛掷至地面以上，形成一个用于投放主战斗部的井道。第二阶段为主战斗部随进和摧毁目标过程，主战斗部爆炸后产生强烈的冲击波与大量高温高压爆轰产物对深埋地下的指挥人员与设备进行致命打击[7-8]。

深钻地掘进武器采用弹载多管火炮完成对侵爆子弹的发射，其内弹道过程与传统火炮具有显著的区别。传统火炮通常采用单药室完成单枚子弹的发射，而“深度挖掘者”中的弹载多管火炮为了形成形状较为规则的投放通道，需要采用单药室完成对多枚子弹的发射。为了研究弹载多管火炮的内弹道性能，本文拟基于经典内弹道计算方法，通过引入身管个数n，建立单药室多管火炮的内弹道计算模型，采用Matlab软件编制内弹道计算程序，以实现对齐射型多管火炮内弹道性能的仿真。

1 掘进系统结构组成

新概念深钻地弹利用弹载多管火炮掘进系统实现大侵深目的，从而显著降低了对弹体速度的要求，降低了战斗部引战配合面临的技术难度。该弹主要包括供电系统、制导系统、着陆系统、掘进系统、有效载荷与控制系统等。掘进系统主要任务是以多枚侵爆子弹的连续侵彻，为终端毁伤战斗部投放提供通道。它主要由火炮身管、纵动式炮闩、自动供弹机、弹药舱、侵爆子弹和全可燃药筒组成，如图1所示。掘进系统是新概念深钻地弹实现其战术目的的关键技术之一，该系统利用侵爆子弹侵彻-爆破联合作用，实现对目标深侵彻的目的。

图1 掘进系统

2 计算模型

经典内弹道方程组为[9-10]：

(1)

齐射型多管火炮具有单个药室多个身管，其火药燃烧规律与经典内弹道火药燃烧规律并无实质性区别，因此形状函数与燃速方程不变。身管个数的增加一方面使弹丸沿膛线部分的摩擦功、火药气体的运动功以及后坐部分的运动功等成倍增加，对次要功系数有重要影响；另一方面火药燃烧产生的气体由药室沿多个身管膨胀，将会引起内弹道基本方程的变化，如图2所示。假设多管火炮各个身管内弹道过程相同，并且不考虑火药燃气流场引起膛内压力的变化，下文将对齐射型多管火炮内弹道方程组进行推导。

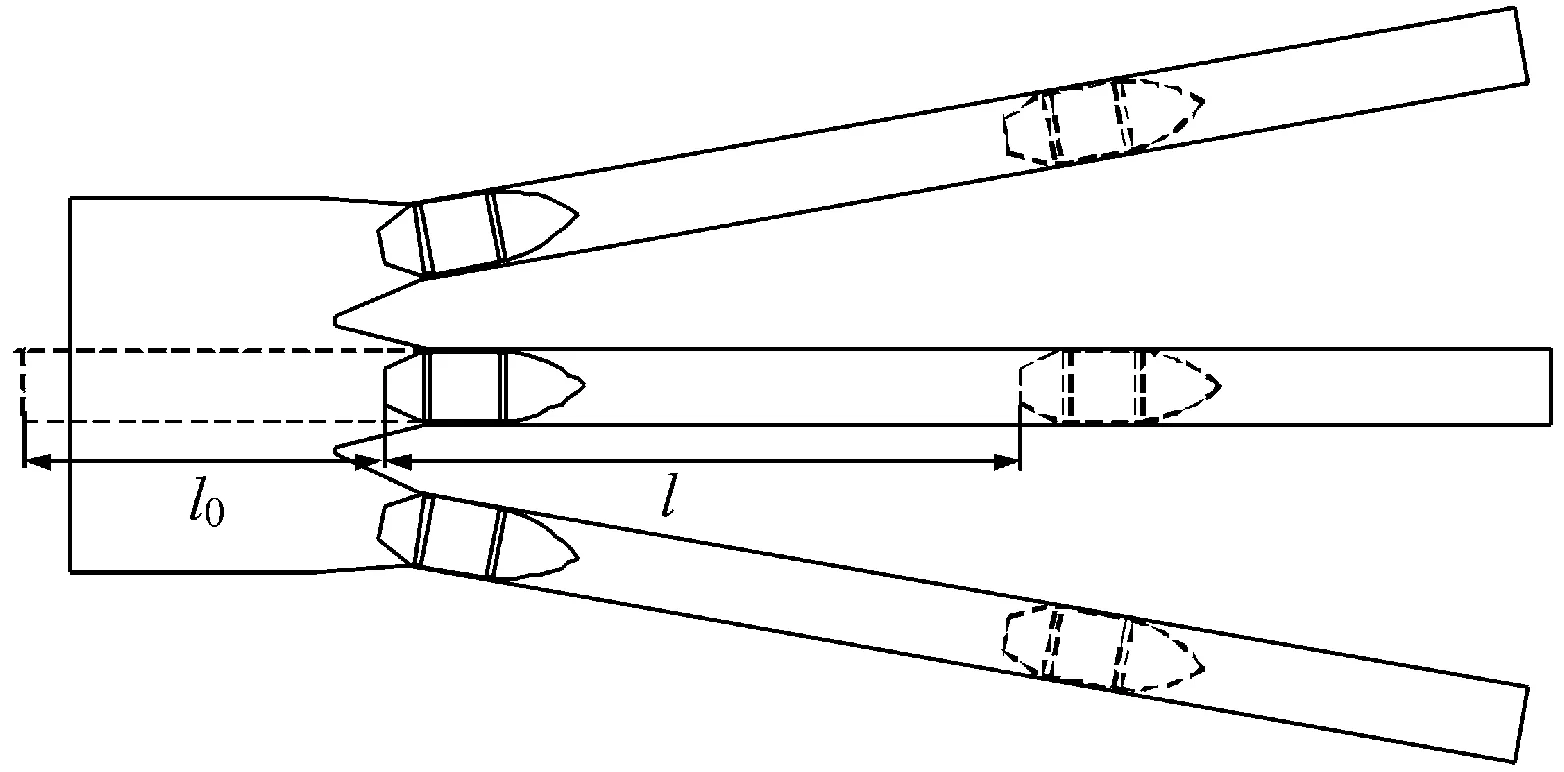
图2 射击时膛内容积变化图解

2.1 内弹道基本方程

设多管火炮身管个数为N，单个身管的横断面面积为S，在药室容积V0中装有质量为ω的火药，火药密度为ρp；假定当火药燃烧到ψ时，单枚质量为m的弹丸向前运动的距离为l，则弹后空间增加的体积为NSl。这时，弹丸后部的自由容积为：

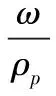
(2)

令

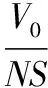
则对于齐射型多管火炮，体现膛内能量转换过程的内弹道学基本方程变换为：

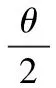
(3)

式中，θ=k-1，k为火药燃气比热比；f为火药力(J/kg)；φ为次要功系数。

2.2 次要功系数

单管火炮次要功系数计算公式为：

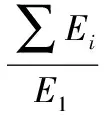
1+K2+K3+K4+K5

(4)

式中，∑Ei为火药燃气所做的总功、E1为弹丸动能、K2、K3、K4、K5分别为弹丸旋转运动所消耗的能量、沿膛线部分的摩擦功、火药气体的运动功以及后坐部分的运动功与弹丸动能之比。

由于管数的增加，齐射型多管火炮弹丸个数也相应的增加，则弹丸旋转运动消耗的能量、沿膛线部分的摩擦功、火药气体的运动功以及后坐部分的运动功也成倍增加。由以上分析可知，齐射型多管火炮的次要功计算公式为：

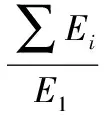
1+K2+K3+K4+K5

(5)

由此可见，管数的增加虽然使次要功成倍增加，但弹丸动能也相应提高，二者的比值则保持不变，即齐射型多管火炮次要功系数与同口径单管火炮相等。

2.3 相对量表示的内弹道方程组

2.3.1 将行程l转换为相对量

(6)

2.3.2 将速度v与压力p转换为相对量

在式(3)中，将火药力f用温度表示，考虑到火药燃气变容状态方程，则有：

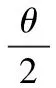
NSp(lψ+l)=ωψRT

(7)

式中:T1为火药燃气生成时的初始温度;T为变容燃烧过程中火药燃气平均温度。

一般情况下，火药通常能在膛内燃烧结束，燃烧结束时ψ=1，设Tg、vg分别表示弹丸出炮口瞬间的膛内火药气体温度和弹丸速度，则在出炮口瞬间有：

(8)

当Tg=0时，弹丸得到在这种装填条件下的极限速度vj，其大小为：

(9)

由V0=NSl0，可得Δ=ω/V0=ω/NSl0，式(6)两端同时除以fω，得：

(10)

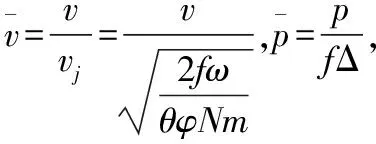
(11)

2.3.3 将时间t转换为相对量

对于速度表达式

把v、l以相对量形式代入，有

2.3.4 引入综合参量B

把相对压力、相对速度、相对行程和相对时间关系代入燃烧速度定律和弹丸运动方程，有

(12)

(13)

(14)

(15)

综合式(11)、(14)、(15)，结合多孔火药几何燃烧规律，可得采用相对量表示的齐射型多管火炮内弹道模型，即：

常量计算公式：

3 等效方法

由以上推导过程可以看出，与单管火炮内弹道方程组相比，齐射型多管火炮内弹道基本方程存在显著差异。然而，将齐射型多管火炮内弹道方程组用相对量表示时，它与经典内弹道方程组具有统一的形式。二者之间的区别在于常量的计算方式不同，如药室容积缩颈长l0、弹丸极限速度vj、综合参量B。此外，从常量计算公式可以看出，身管个数N总是与药室容积V0或装药量ω成对出现，这为齐射型多管火炮的内弹道计算等效方法的提出提供了可能性。

齐射型多管火炮内弹道等效方法可以从单个身管或所有身管形成单个身管考虑，相应的等效方法本文称之单管等效与多管等效。身管是将药室内火药能量转换为弹丸动能的装置，通常火药质量越大，弹丸速度就越高。对于齐射型多管火炮中的任意一个身管，推动弹丸做功的火药应为总药量的N分之一；此外，为了保证装填密度Δ不变，药室容积也应变换为原容积的N分之一，这种方法称为单管等效。如果考虑所有的身管组成一个更大的身管，则药室容积V0与装药量ω不变，而身管横截面积为单个身管的N倍，并且此时火药能量对所有弹丸加速，弹丸质量也应为单个弹丸质量的N倍，该种方法称为多管等效。等效参数变换如表1所示，从表中可以看出，采用等效方法计算得到的常量与前文推导完全一致。

4 齐射型多管火炮内弹道计算

采用Matlab软件编制内弹道计算程序，对掘进系统中的多管火炮进行内弹道性能仿真，输入的原始数据如表2所示，内弹道计算结果见图3。

表1 等效法参数变换及常量计算

表2 齐射型多管火炮原始数据

余容α/(m3·kg-1)1×10-3装药量ω/kg0．378燃速指数n0．75燃速系数u1/(m·Pa-n·s-1)8．6×10-7火药种类6/7火药厚度2e1/m0．0082孔道直径d0/mm0．015药粒长度2c/mm0．08孔数n7身管个数N7

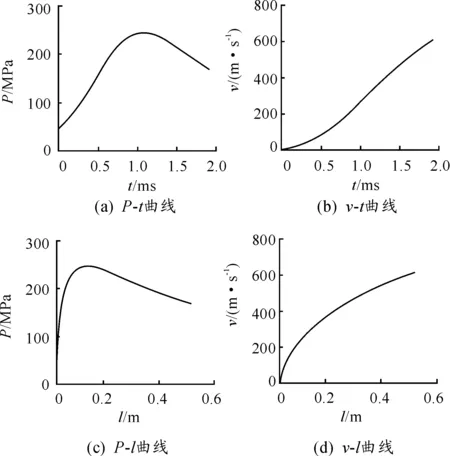
图3 齐射型多管火炮内弹道计算结果

[1] 于雪泳, 朱清浩.美军钻地弹的发展使用及其防御技术综述[J].飞航导弹, 2012(11):56-58.

[2] 王涛, 余文力, 王少龙.美军钻地武器的现状及发展趋势[J].飞航导弹, 2004(8):4-7.

[3] 石艳霞, 郝丽萍.国外钻地武器的技术特点及发展趋势[J].导弹与航天运载技术, 2003(4):50-53.

[4] 刘永远, 姜正平, 张进.钻地弹及其发展趋势[J].飞航导弹, 2006(3):34-37.

[5] 周义, 王永良, 王自焰.地下堡垒克星——美军钻地弹的应用与发展[J].飞航导弹, 2005(4):41-45.

[6] WANG H, XIAO J, ZHENG Y, et al.Failure and Ejection Behavior of Concrete Materials under Internal Blast[J].Shock and Vibration,2016,(2016-1-5), 2016, 2016(5):1-7.

[7] DAVID BURNS.Deep digger weapons system concept[C]//Medium Caliber Weapons Systems Branch, US Army ARDEC, 41st Annual NDIA Gun and Missile Systems Conference, 2005:1-14.

[8] DAVID BURNS.Deep digger weapons system development[C]//Medium Caliber Weapons Systems Branch, US Army ARDEC, 42st Annual NDIA Gun and Missile Systems Conference, 2006:1-22.

[9] 金志明.枪炮内弹道学[M].北京：北京理工大学出版社, 2004.

[10] 鲍廷玉.内弹道学[M].北京：北京理工大学出版社, 1995.

SimulationofInteriorBallisticPerformanceforMultiple-VolleyGun

XIAO Jianguang1, ZHENG Yuanfeng2, GUO Zhangxia1, LIU Zongchao3, GAO Yuefei1

(1.College of Mechatronic Engineering, North University of China, Taiyuan 030051, China; 2.State Key Laboratory of Explosion Science and Technology, Beijing Institute of Technology, Beijing 100081, China;3.Inner Mongolia North Heavy Industries Group Corp.Ltd., Baotou 014033, China)

Interior ballistic equations set available for multiple-volley gun is developed by introducing the number of barrels as new parameter. The results show that the interior ballistic basic equation is remarkably different from that of classic interior ballistic equations set, because propellant gas has expanded in more barrels. More barrels manyfold increase the secondary work while the projectile kinetic energy increases accordingly, therefore, the coefficient of secondary work of multiple-volley gun, which represented by the ratio of the two, remains the same to that of identical caliber single barrel gun. Interior ballistic equations set for multiple-volley and single barrel gun has uniform shape when expressed by relative quantities. The differences are just in the constant calculation equations, such as the equivalent length of chamber volumel0, maximum velocity of projectilevj, synthesis parameterB, and so on. Based on the comprehensive analysis on these constant calculation equations, two equivalent methods for multiple-volley gun, single barrel equivalent and multiple barrels equivalent, are proposed in this paper.

deep digger weapons system; volley gun; multi-barrel gun; interior ballistic simulation; equivalent method

2017-08-20；

2017-09-12

肖建光(1984—)，男，博士，主要从事新概念火炮、高效毁伤弹药等方面的研究。

10.11809/scbgxb2017.12.001

本文引用格式：肖建光,郑元枫，郭张霞，等.齐射型多管火炮内弹道性能仿真[J].兵器装备工程学报，2017(12):1-5.

formatXIAO Jianguang, ZHENG Yuanfeng, GUO Zhangxia, et al.Simulation of Interior Ballistic Performance for Multiple-Volley Gun[J].Journal of Ordnance Equipment Engineering,2017(12):1-5.

TJ414.+3

A

2096-2304(2017)12-0001-05

(责任编辑周江川)