基于大数据技术的军事比武路径优选方法研究

姚俊萍　李新社　李晓军

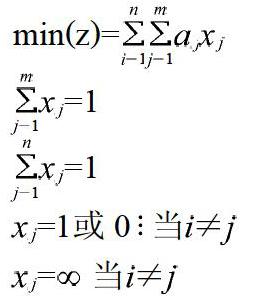
摘 要 数据已经成为信息化时代的关键生产要素，将大数据技术应用于军事领域具有重要的意义。本文首先利用百度地图中的大数据，计算出军事比武中待经过点之间的距离，然后设计算法变换距离数据表使得零个数达到最多，最终得出军事比武距离中的最短路径，从而节省了时间，提高了部队战斗力。

关键词 大数据 优化 最短路径

中图分类号：TP274 文献标识码：A DOI：10.16400/j.cnki.kjdkz.2018.10.035

Abstract Data has become a key production factor in the information age； applying big data technology to the military field is of great significance. We calculate the distance between points in military contest based on big data in Baidu Maps， design algorithms to transform the distance data table to maximize the number of zeros， and find the shortest path in the military distance in this paper. It improves the combat effectiveness of the troops effectively.

Keywords big data； optimization； shortest path

大数据常用的分析方法有统计、数据挖掘、预报、文本挖掘和优化。优化方法从前一直被忽视，但发展前景不可小视。比如军事比武路径优选、安全警勤巡查路线优选、武器快速配发、快件快速投递，将优化方法应用在这几个领域，可以节约资源、节省时间，尤其是在军事斗争领域可以提高战斗力。这里以军事比武路径优选为例，每个参与比武的选手必须在某个区域内的所规定位置必须巡视一次，也只需一次，然后回到出发点。至于如何规划行走路线可以八仙过海，各显神通。再假设比武工具为摩托车，几乎不受交通影响，且各道路行走难易程度一样。

如何规划行走路线使得耗费最低？对一个选手来说，固有技能已经确定，关键是选择行走路线，显然行走路线最短的一条应为首选。巡视点位确定后，任意两个巡视点的距离可以通过百度地图计算出来。一个可以但比较坏的想法是通过排列组合进行穷举比较选择，该种想法只有在巡视点很少情况下才可以，否则计算量很大，难以实现。

1 研究基础及其依据

假设巡视点为A、B、C、D、E、F，通过百度地图计算各巡视点的距离如表1所示。

当不等于时为百度地图计算出的值，等于时为∞。

定义 矩阵代表各点之间的计算距离，为求解结果，于是行走路线问题转化为如下求解最小值的数学模型问题。

其中，的每行每列都只有1个1，其余为零，说明每个点只能从其他一个点到达。通过这个解可以形成一个路线，该路线经过所有点，除回到出发点外，每点只经过一次，关键是路线距离最短。

数据表中的一行（列）各元素减去该行列的最小元素，得到新的表格数据。原、新两个表格数据求解结果相同，这是因为到某点距离同时增大或缩小相同值与选择合适路径无关，犹如在五个数中选出最小的那一个，所有数据同时增加或减小相同值不改变选择的对象。

若能通过数据表变换，在数据表中找出个独立的0元素，然后令中对应这个独立的0元素取值为1，其它元素取0，也就得到了原问题的最优解。因为这样就可使 达到最小，且实现了选择最短路线的目的。

2 算法构建

我们的方法是通过数据表的行（列）变换，寻找个独立的0。下面是變换的方法步骤。

第一步，利用行（列）减其最小值，使得变换所得系数矩阵中含有很多0元素。

第二步，计算覆盖所有0元素的行和列数，确定该数据表中能找到最多的独立0元素个数。

（1）从只有一个0元素的行（列）开始，然后划去所在列（行）的其他0元素，记作 ；

（2）重复执行（1），若同行（列）的0元素至少有两个，比较这行（列）各0元素所在列（行）中0元素的数目，选择0元素少的那列的0元素，然后划掉同行同列的其它0元素。可重复执行，直到所有0元素都已圈出或划掉。

（3）对没有0元素的行打√，然后对已打√的行中所含元素 的列打√，再对打有√的列中含有0元素的行打√，直到得不出新的打√的行或列为止。

（4）计算没有打√的行数和有打√的列数的和，就得到0元素独立个数。若少于总点数，则需要重新变换数据表。

注意，从第二次开始执行数据表变换时，选取打√行中所有元素的最小值（除 元），打√行各元素都减去这个最小值，而打√列各元素都加上这个最小值，得到新数据表。

3 实例验证

（1）设巡视检查的点位为A，B，C，D，E，F；通过百度地图计算所得的任意两点距离（自己到自己定义为∞），结果如表2。

（2）对表格按照算法步骤的第一步对数据表进行变换得表3。

（3）对表3按照算法步骤2打√，得表4。

（4）由表3知，没有打√的行数和打√的列数之和为4，小于总点数，此时选取表3中打√行中所有元素最小值（除 元），打√行各元素都减去这个最小值，而打√列各元素都加上这个最小值，得新数据表5。

（5）对表4进行打√，得表6。

（6）由表6知，没有打√的行数和打√的列数之和为5，小于总点数，此时选取表-6中打√行中所有元素的最小值（除 元），打√行各元素都减去这个最小值，而打√列各元素都加上这个最小值，得到新数据表7。

此时，此时发现列中元素出现负值，让该列各元素加上最小值的绝对值，得数据表8。对表8进行打√，得表9。

（7）由表9知，没有打√的行数和打√的列数之和为5，小于总点数，选取表8中打√行中所有元素的最小值（除 元），打√行各元素都减去这个最小值，而打√列各元素都加上这个最小值，得到新数据表10。

对表10按照算法第二步的（1）和（2）处理后，得到表11和表12，没有可打√的，计算结果为6，0独立元素个数为6。

（8）将表10和表11转化为最优解，即为表13，表14。

从表12和表13立刻可以得出最优路线A——D——E——F——C——B，或A——B——C——F——E——D。

4 结论

整个算法基于数据表，利用的变换只有加减法，没有复杂乘法、求逆等，计算量很小，可以通过编程有效实施完成。于是也就可以利用该算法快速解决武器快速配送分发、急行军路线优化选择、重要安全场地巡视等问题。

参考文献

[1] Martins E Q，Santos J L.A new shortest paths ranking algorithm[J].Investigacao Operacional，2000.20（1）：47.

[2] 于海璁，陆锋.一种基于遗传算法的多模式多标准路径规划方法[J].测绘学报，2014（1）：8.

[3] 宋晓宇，许鸿斐，孙焕良等.基于签到数据的短時间体验式路径搜索[J].计算机学报，2013.36（8）：1693.

[4] 唐炉亮，常晓猛，李清泉.出租车经验知识建模与路径规划算法[J].测绘学报，2010（4）：404.

[5] 毕马威中国大数据团队.洞见数据价值大数据挖掘要案纪实.清华大学出版社，2018.

[6] 赵卫东，董亮.数据挖掘实用案例分析.清华大学出版社，2018.2.

[7] James Evans.Business Analytics[M].New York：Person Education Limited，2017.

[8] 陈春宝，钟飞等.大数据与机器学习实践方法与行业案例[M].机械工业出版社，2017.