齿线有曲线方程吗

周田虎+黄元华

齿轮是日常生产生活中常见的传动设施。本文中，我们称类似齿轮轮廓线的曲线叫齿线。齿线可以有各种形状，如机械手表的机芯为圆形齿线，木工用的锯条为直线型齿线。当然也可以根据特殊需要设计其他形状的齿线。我们感兴趣的是各类齿线是否存在一种具有一定规律可循的曲线方程？带着这个问题，笔者经过初步探究，得到了一种简单实用的构造各种形状齿线方程的方法。

一、课本原题的推广

新课标高中数学教材必修4（北师大版）第一章三角函数中有一道习题：利用五点法或借助信息技术画出函数y=sinx-|sinx|的图像。

本题难度不大。笔者对本题展开了一般化研究，借助几何画板，画出了更多的形如y=a+b（sinnx±|sinnx|）（a，b∈，b≠0，n∈*，下同）的函數图像，发现它们均呈齿线形状。图1为函数y=2+0.2·（sin10x-|sin10x|）（x∈[-2仔，2仔]）的图像。

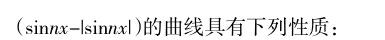
（1）在[0，2仔]上曲线的齿数为n；

（2）齿长（齿尖到直线y=a的距离）为2|b|；

（3）当b>0时齿尖向下，当b<0时齿尖向上。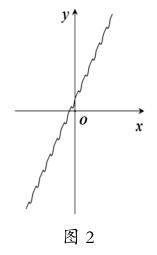

二、齿化曲线的方程

我们尝试把方程y=a+b·（sinnx-|sinnx|）中的a换为kx+m，即得方程y =kx +m +b（sinnx-|sinnx|）。例如，y=2x+1+0.2（sin10x-|sin10x|），借助几何画板，画出其曲线，如图2。可以说，方程y= 2x+1+0.2（sin10x-|sin10x|）把直线y=2x+1齿化了。

一般地，若曲线C：y=f（x），则曲线C忆：y=f（x）+ b（sinnx-|sinnx|）（b≠0）①为曲线C的一种齿化曲线，称①为曲线C的齿化曲线方程。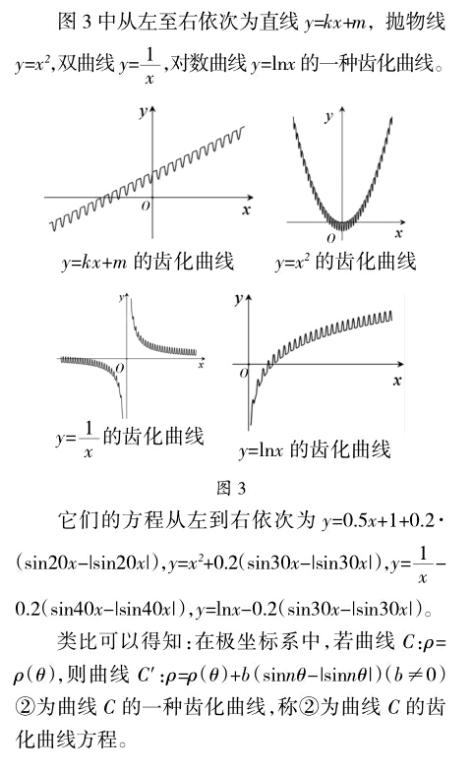

利用几何画板，可以画出极坐标系中圆C：籽= 2的一种齿化曲线C忆：籽=2±0.2（sin20兹-|sin20兹|）。

图4中左图的方程为籽=2 + 0.2·（sin20兹-|sin20兹|），右图的方程为籽=2-0.2·（sin20兹-|sin20兹|）。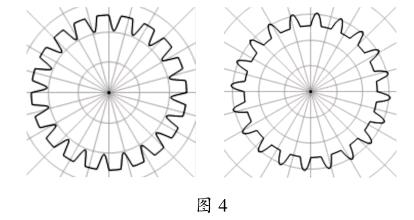

这里，我们不仅得到了两个非常漂亮的齿线，也得出了一种具有实用价值的设计圆形齿线的简洁方法。依照这个方法我们就可以根据齿轮的多少、齿长的大小等要求设计齿轮。

图5是极坐标系中的一些曲线的齿化曲线。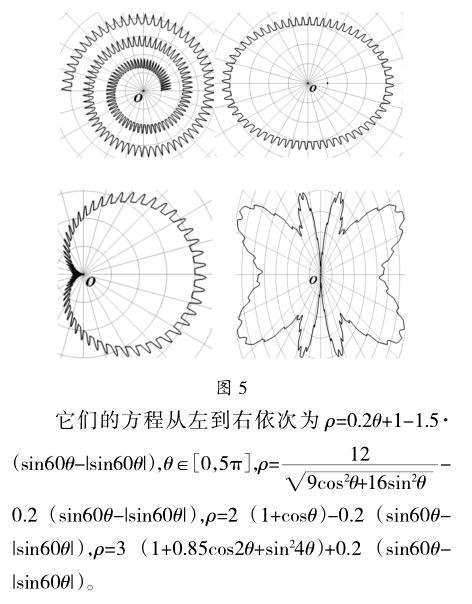

容易知道，若把上面的（sinnx-|sinnx|）换成另外一些具有一定周期的齿形函数，将可得到很多千姿百态的齿线，有兴趣的读者不妨继续探讨。

（作者单位：广东省深圳高级中学）