基于TOF相机的机械部件快速重建与测量方法

王 涛，薛少辰，梁 梓

（中国人民解放军陆军装甲兵学院车辆工程系，北京 100072）

基于TOF相机的机械部件快速重建与测量方法

王 涛，薛少辰，梁 梓

（中国人民解放军陆军装甲兵学院车辆工程系，北京 100072）

针对机械类装备教学工作开发的维修训练增强辅助系统，为修理人员训练提供了与指导人员实现多维信息交换的交互平台。基于TOF相机的深度图增强算法原理，基于Kinect的旋转刚体三维重建方法，通过对机械部件三维点的云获取以及线、面、体的几何测量，完成对整个部件的三维重构建模，以应用于机械维修训练增强辅助系统中。

TOF深度图像；三维重建；点云计算；配准

10.16621/j.cnki.issn1001-0599.2017.12.55

0 前言

机械类装备功能的多样性需求使得安装在其上的设备在结构上和原理上复杂多样，对维修人员的知识广度和深度要求较高，多数维修保障人员的能力还不能满足现实维修保证需求。随着科学技术水平的不断发展，20世纪90年代初，增强实现技术应运而生，该技术英文简称为Augmented Reality，此时该技术成为相关学者研究热点。这一技术实际应用中，主要通过虚实结合实现零件模型的有效组合，同时，优化装配真实空间，进而有利于优化装配效果，有利于营造良好的装配环境，此外，交互方式能够具体应用[1]。一套行之有效的对机械类装备各部件进行快速三维重构和测量，从而建立虚拟三维模型的方法是必要的。

1 研究现状

1.1 TOF相机原理

TOF（Time of Flight）相机以微软公司的价格低廉的Kinect为媒介，包含彩色摄像头、深度（红外）摄像头、红外线投影机以及4个麦克风[2]。其中彩色摄像头用于拍摄彩色视频图像；红外投影机投射近红外光谱，接受前方不光滑的物体或毛玻璃产生的扭曲散斑，处理反射信息，获取物体成像像素的深度值，生成深度图像。4个麦克风组成四元线性麦克风阵列，处理声音信号，过滤背景噪声，定位发生源方向。由于在深度图像中，场景中物体到相机的距离可以其深度值表示，因此场景中物体的三维结构信息可以通过深度值体现。与传统的彩色图像相比，深度图像在人体姿态估计、目标检测等领域都有着更为广泛的应用前景[3]。

1.2 国内外研究现状

目前，国内学者以及其他外国学者在探究三维重建技术的过程中，适当应用Kinect于其中，主要有4种方式。

（1）保持被研究对象以及所在场景于静止状态，与此同时，适度改变Kinect位置，完成深度图像的有效收集，最终完成重建任务[4]。

（2）站在特定角度实施相关深度图像获取活动，在此期间，提高Kinect的应用率，基于此，在短时间内高效重建，某大学著名研究学家对此从不同角度进行信息收集和整理，以便为重建工作提供有力数据支持[5]。

（3）这种方式不同于上述两种，它主要变动物体位置，此时Kinect处于静止状态，以此获取深度图像，完成最终的重建任务，文献[6]中提出了具体的重建方法。

（4）在非匀速非定轴条件下，通过固定位置Kinect采集二维深度图像，并通过点云计算和配准完成全局三维坐标下所有点的表示[7]。装甲车辆部件工作时相互间运动复杂，同时一般属于刚性物体不存在尺度变换，适用于非匀速非定轴刚体条件下的三维重建算法。

2 三维重构

2.1 重构流程

针对三维重建法进行重构流程分析时，将分析条件设定为非匀速非定轴旋转，与此同时，应用Kinect，具体步骤主要有[10]：深度图像获取，固定Kinect获取部件非匀速非定轴旋转中深度图像；事先处理，深度图像获得后，需要进行预处理操作，处理内容分别为去背景、降噪处理；点云计算。计算各点的三维坐标和法向量，由以上6个值组成点云；配准，表示坐标点的过程中，应做好矩阵变换、坐标系转换等工作；映射，求TSDF（Truncated Signed Distance Function，截断符号距离函数）值的过程中，常用加权平均法完成求值工作[11]，实现物体各点从全局三维坐标系到各个体素上的映射；修正，为了提高数据处理源质量，增加数据处理源的准确性，务必实施映射、加权平均法，针对所获得的体素值合理调整、有效修正，最终获取点云数据[12]；表面生成，由于立方体体素数量相对较多，针对等值面获取的过程中，适当应用移动立方体算法[13]，以此生成整体表面。

2.2 三维点云获取

Kinect通过Depth Generate（r深度发生器）得到实际的深度值，单位是mm。即该点与Kinect所在呈90°角。确定世界坐标系，即[R，t]=[I，0]，深度图像上的值即为世界坐标系下的值ZW，对应相应的图像平面的点（u，v），由相机成像原理及投影方程得式（1）。

由于相机内参K以及u，v，ZW己知，可得世界坐标系下坐标为式（2）。

XW，YW，ZW，即点（u，v）对应的世界坐标系下的坐标。通过计算各点、在世界坐标系下的坐标，获得深度图像。

2.3 点云ICP精确配准

采用基于迭代的ICP精确配准算法[14]，对于数据集P中的每个数据点，在目标数据集中找到相应的最近点集Q，该过程记为Q=c（P，T），己知控制点集P，Q，变换矩阵参数的估计记为（H，d）=q（P，Q）。对数据集中的每个点，经过变换矩阵H更新后记为H（P）=R（P）+T。设S为源数据集，设T为目标数据集，初始令 P0=S，R0=I，T0=0，k=0，则 ICP 算法迭代步骤如下。

（1）计算最近点。对Pk的每个数据点，估计目标数据集T中最近点集Qk。

（2）估计配准参数。使目标函数最小化，估计配准参数式（3），计算估计误差 dk。

（3）更新源集，用得到的配准参数Hk，对数据集进行更新，其中 Pk+1=H（kP0）=R（kP0）+Tk；重复迭代：当阈值 ε＞两次估计得到的误差变化时，即||dk-dk+1||＜ε时，迭代停止。

在目标数据集中找出源数据集P中每个点的对应点，对刚体的运动参数进行估计。寻求对应点的方法有最近点匹配、法向投影匹配和相机投影匹配。采用不同的匹配方法通常依赖于数据的几何模型和数据集之间的重叠情况。

2.4 模型表面构建

采用TSDF点云融合和移动立方体算法（Marching Cubes）完成模型表面的构建[15]。根据配准变换参数，与此同时，实现世界坐标的有效转化，数据立方体相应体素内具体投射世界坐标。数据加入模型时，按照式4和式5融合处理，式中di+1表示加入新点云的数据后当前点云对应的SDF（Signed Distance Functions）值，Di表示原有的TSDF加权值。通过权重W 进行融合，新的权重为两权重之和，在KinectFusion算法中当前点的云权重为1。

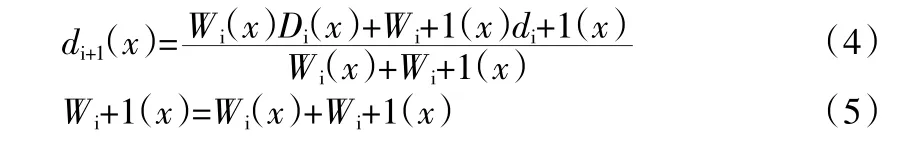
移动立方体算法是一种基于体素（voxel）的表面构建方法。该方法应用的过程中，字母V代表等值面值，同时，假设立方体的棱上值线性变化。如果8个顶点TSDF值均＞或＜V，则等值面重合于该立方体；反之不重合。对于棱，如果两个端点值均＞或＜V，则该棱与等值面不相交；反之有交点，对于棱与等值面的交点，常用线性插值法予以获取。通过组合三角片法实现相同立方体的交点连接，最终形成的面能够代表等值面。

3 几何测量

3.1 对两点间表面距离的测量

本文使用带约束条件的特殊二叉查找树kd-tree（kdimensional tree）算法[16]，采用FLANK，快速最近邻点检索库搜索每个顶点半径为r的邻域的邻接点集合，计算其与顶点间的距离。从点云中构建图结构，每个顶点与其邻接点相连构成图的边，欧式距离作为该边权值。

图中两点之间的最短距离由单源最短路径算法Dijkstra[17]算法得到。设G=（V，E）是一个带权无向图，V和E分别为图中所有顶点集合和所有边集合，假设源点为V0，针对最短路径查找所应用的算法主要有：将顶点集合V分成包含所有己计算出源点到该顶点最短距离的顶点集合S和包含所有未计算出源点到该顶点最短距离的顶点集合U；初始状态，S中只有源点，即S=｛V0｝，U包含了V中除V0外的所有其他顶点。V0到U中任意顶点u的初始距离为：如果存在边＜V0，u＞，边上的权值由两顶点间初始距离表示；如果不存在边＜V0，u＞，

则两顶点间初始距离为无穷大；在u中选择与V0距离最小的顶点k，把k从U移除并添加到S中，更新U中所有顶点到V0的距离：如果从源点V0经k到U中任意点u的距离比原先的距离（即不经过k）短，则更新＜V0，u＞的距离值，新的值为源点到 k 的距离与边＜k，u＞的权值之和，同时，把＜V0，u＞加入源点 V0到u的最短路径中。重复（3），在U中选择与k距离最小的顶点，直到U为空，S中包含所有顶点。

3.2 基于三角网格模型对封闭区域体积的测量

通过构建三角网格模型，指定投影平面，计算三角面片及其在投影平面上的投影三角形围成凸五面体的带符号体积，整个模型体积即其代数和。

与所有三角面片均不相交的任意平面均可作为投影平面，设其z=zmin，其中zmin为三角网格模型顶点Z坐标的最小值。若投影平面不平行于XOY平面，可通过适当的三维旋转变换使投影平面与XOY平面平行。

任意三角面片t和投影平面围成的凸五面体Pt可分为一个三棱柱和2个四面体，其体积和即为凸五面体体积Vt。4个顶点坐标分别为（x1，y1，z1）（，x2，y2，z2），（x3，y3，z3）和（x4，y4，z4）的四面体体积，见式（6）.

需确定各三角面片投影体积的符号：正号在计算时加上该四面体体积，负号则减去。判断符号依据如下[18]：

对于所有三角面片围成的封闭三角网格模型，令三角面片集合为T，其中任意三角面片t在投影平面的投影三角形为tD，计算三角面片集合见式（7）。若集合 At中任意 t和 t′均有 tD⊆tD′或 tD∩tD′=Ø，则 t投影符号为（-1）|At|+1。At计算方法如下。

（1）计算t与投影三角形tp，判断两三角面片的投影三角形的包围矩阵是否有交集，若无交集则两投影三角形无交集。

（2）若满足（1），继续判断两投影三角形各边是否有交集，若是，则相交；若不满足（1），判断两投影三角形是否相互包含，如果不相互包含，那么两投影三角形不相交，反之，则相交

3.3 基于三角网格模型对表面积的测量

同样指定一个平行于XOY平面的投影平面z，通过At和三角面片的方向矢量（x0，y0，z0），可计算出每个三角面片的面积A见式（8），部件的表面积可以简单的用这些三角面片面积之和表示。

4 结论

通过TOF相机获取深度图像，在非匀速非定轴旋转条件下，对获取的点云数据进行精确配准和修正，根据数据进行线、面、体的几何测量，并最终形成基于TOF相机的机械类装备的三维重建方法和测量方法，以应用于机械类装备维修训练增强辅助系统中，为机械类装备维修和教学工作提供了有效支撑，同时为增强现实技术在维修领域的应用研究提供参考。

［1］李阳.基于NyARToolkit的实时增强现实动员仿真系统开发研究［D］.北京：北京交通大学，2015.

［2］邬冠上.基于Kinect的交互式健身游戏的设计与实现［D］.中国科学院大学，2014.

［3］陈理.Kinect深度图像增强算法研究［D］.长沙：湖南大学，2013.

［4］刘金荣，李淳亢，欧阳建权，等.基于联合双边滤波的深度图像增强算法［J］.计算机工程，2014，40（3）:249-252.

［5］刘俊毅.彩色图像引导的深度图像增强［D］.浙江大学，2014.

［6］Kopf J，Cohen M F，Lischinski D，et al.Joint bilateral upsampling［J］.Acm Transactions on Graphics，2007，26（3）:96.

［7］Yang Q，Yang R，Davis J，et al.Spatial-Depth Super Resolution for Range Images.［C］.//IEEE Conference on Computer Vision and Pattern Recognition.IEEE Computer Society，2007:1-8.

［8］Paris S，Durand F.A Fast Approximation of the Bilateral Filter Approach［J］.International Journal of Imaging Systems&Technology，Using a Signal Processing2008，18（2-3）:124-136.

［9］NasonovA V，KrylovA S.FastSuper-Resolution Using Weighted Median Filtering［C］.//on Pattern Recognition.IEEE Computer Society，2010:2230-2233.

［10］韦羽棉，尚赵纬.基于Kinect的旋转刚体三维重建方法［J］.计算机与现代化，2014.5

［11］NewcombeR A，IzadiS，Hilliges，etal.KinentFusion:Realimedense surfane mapping and tracking［C］.//Pro-needings of the 2011 IEEE International Symposium Mixed and Augmented Reality.2011:127336.

［12］IzadiS，Kim D，Hilliges0，etal.KinectFusion:Real-time 3D reconstruction and interaction using a moving depth camera//Proceedingsofthe 24th AnnualACM Symposium on User Interface Software and Technology.2011:559-68.

［13］Curless B，Levoy M. A volumetric method for building complex modelsfrom rangeimages［C］.//ProneedingsofSIGGRAPH 1996.1996:303-12.

［14］Besl P J，McKay H.D.A method for registration of 3-D shapes.IEEE.Transactions on Pattern Analysis and Machine Intelligence，1992，14（2）239-256

［15］Lorensen W E，Cline H E.Marching cubes:a high resolution 3D surfacealgorithm［C］.ACM Siggraph ComputerGraphics.ACM，1987，21（4）:163-169.

［16］刘艳丰.基于kd-tree的点云数据空间管理理论与方法［D］.长沙：中南大学，2009.

［17］严蔚敏，吴伟民.数据结构（C语言版）［M］.北京:清华大学出版社，2007.

TP75

B

〔编辑 凌 瑞〕