天然地基软弱下卧层顶面附加压力计算方法探讨
2018-01-03孙君
孙 君
(常州市规划设计院,江苏常州 213000)
天然地基软弱下卧层顶面附加压力计算方法探讨
孙 君
(常州市规划设计院,江苏常州 213000)
天然地基软弱下卧层承载力验算的关键,为下卧层顶面附加压力的计算。目前规范尚未明确1≤ES1/ES2<3时软弱下卧层顶面的附加压力计算方法,本文分别采用附加应力系数法和地基压力扩散角法(含叶戈罗夫理论解法、高大钊建议方法及地方规范提供方法),同时考虑了压缩模量比和计算深度的变化,对各计算方法下卧层顶面附加压力计算结果进行了分析对比,并给出1≤ES1/ES2<3时软弱下卧层顶面附加压力的计算方法建议。
软弱下卧层;压缩模量比;附加应力系数;地基压力扩散角
0 前言
软弱下卧层是指承载力小于持力层的下卧层(高大钊,2010年),建筑地基基础设计规范(GB50007-2011)(后简称“规范”)(中国建筑科学研究院,2010年)要求当地基受力层范围内存在软弱下卧层时,应进行软弱下卧层地基承载力验算,而验算的关键是计算软弱下卧层顶面处的附加压力值。
规范采用地基压力扩散角简化计算式(1)、式(2),并分别给出了压缩模量比ES1/ES2为3、5、10时的地基压力扩散角,用于计算软弱下卧层顶面处的附加压力。
条形基础:

矩形基础:
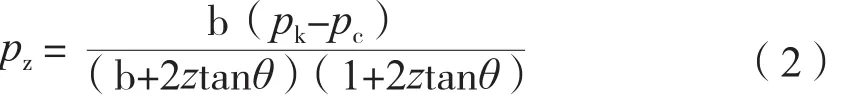
而在工程实践中,常常出现1≤ES1/ES2<3的情况,此时软弱下卧层顶面的附加压力如何计算,规范尚未明确。
1 软弱下卧层顶面附加压力计算方法
当1≤ES1/ES2<3时,目前文献提出的软弱下卧层顶面附加压力计算方法主要分两类:附加应力系数法、地基压力扩散角法。
1.1 附加应力系数法
1≤ES1/ES2<3时,由于持力层和下卧层压缩模量差异不明显,很多学 者(隋艳革等,2001年;余晓东,2001年;孔祥国,2004年;张启兵,2008年;张高峰,2007年)提出可近似看作均质地基,采用附加应力系数法计算软弱下卧层顶面附加压力。
附加应力系数法假定地基为均质的线性变形半空间,即压缩模量和泊松比各处相等,采用弹性力学Bousssinesq 公式计算。
按附加应力系数法计算时,软弱下卧层顶面各点的应力值不同,中心点处最大,远离中心点逐渐减小。从安全角度考虑,验算时取软弱下卧层顶面中心点处的附加应力值。
1.2 地基压力扩散角法
(1)叶戈罗夫理论解
地基压力扩散角的确定主要有两种方法:试验法和理论解。追溯规范下卧层验算公式的来源和理论依据,地基压力扩散角θ的取值和应用条件是在双层地基叶戈罗夫理论解和试验统计数据两者综合分析的基础上确定的。试验法最直观,与实际情况吻合度高,但由于试验条件、试验数量、土性差异的局限以及硬土层厚度的不同,很难得出各种工况下的压力扩散角,理论法确定压力扩散角不失为一种有效解决方法(茅卫兵,2007年)。
根据规范条文说明中的叶戈罗夫理论解换算所得地基压力扩散角表格(张晓范,2007年)(表1),建议采用线性内插求出1≤ES1/ES2<3的地基压力扩散角,整理后如表2。

表1 规范中地基压力扩散角理论解Tab.1 Theoretical solution of expansion angle of subgrade pressure in nation standard
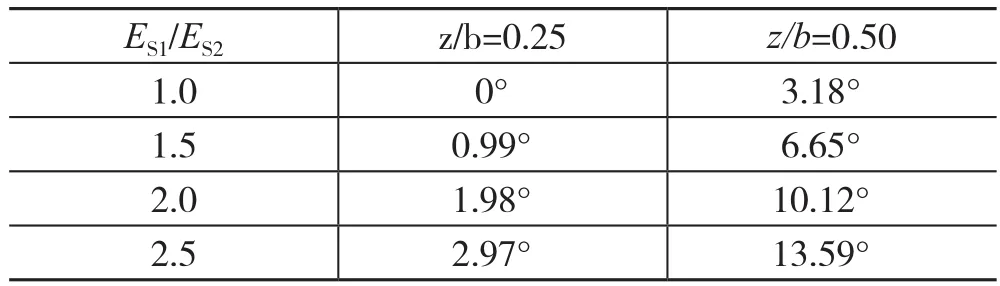
表2 1≤ES1/ES2 <3的地基压力扩散角内插理论解Tab.2 Interpolation theoretical solution of expansion angle of subgrade pressure in the case of 1 ≤ ES1/ES2 <3
(2)高大钊建议方法
高大钊(2010年)建议在1≤ES1/ES2<3情况下,优先采用附加应力系数法计算软弱下卧层顶面附加压力,同时也认为此时用模量比为3时的扩散角计算的结果和均质土的应力计算结果接近,建议仍可用压缩模量比等于3的扩散角计算软弱下卧层顶面附加压力。
(3)地方规范法
部分地方规范(浙江省建设厅,2003年;天津市城乡建设委员会,2000年)明确了1≤ES1/ES2<3情况下的θ值,并通过内插整理为表3。
2 多种计算方法的对比分析
2.1 算例
天然地基方形基础,基础边长b,基底附加应力为p0,计算ES1/ES2=1、1.5、2、2.5情况下,基础底面至软弱下卧层顶面距离z分别取0.25b和0.50b时的软弱下卧层顶面附加压力值。

表3 地方规范中地基压力扩散角Tab.3 Expansion angle of subgrade pressure in local standards
计算思路:
(1)附加应力系数法:基础等分为4个小正方形,根据规范附录K查出小正方形角点下对应深度处的附加应力系数α值,再叠加计算附加应力即可。
(2)地基压力扩散角法:将式(2)简化为式(3)和式(4):
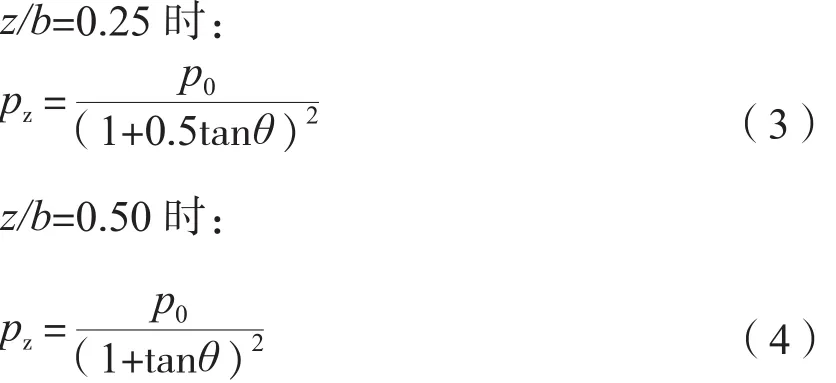
分别将各方法对应的θ值带入即可求得对应深度处的附加应力值。
2.2 多种方法计算结果
采用附加应力系数法、叶戈罗夫理论解法、高大钊建议方法、地方规范法分别计算出ES1/ES2=1、1.5、2、2.5时,z=0.25b和z=0.50b处的附加应力值,如表4、表5所示。

表4 z/b=0.25时的pz值Tab.4 Vulue pz when z/b=0.25
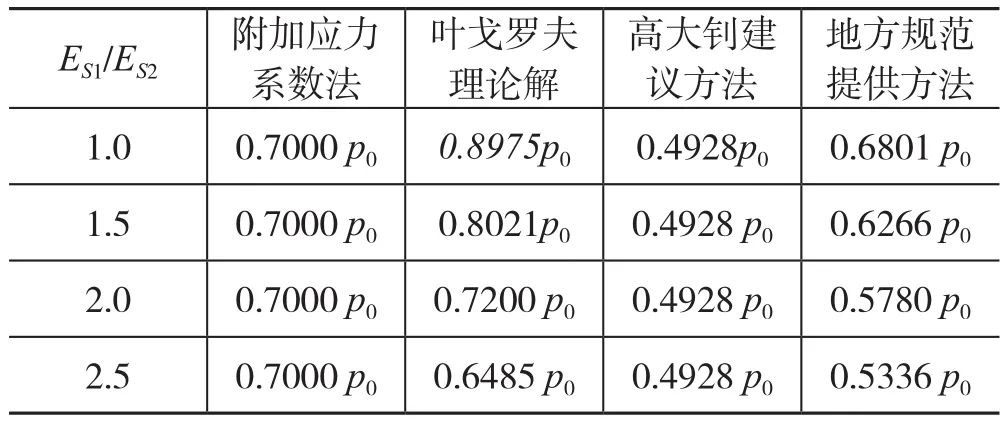
表5 z/b =0.50时的pz值Tab.5 Vulue pz when z/b=0.50
2.3 各计算方法对比分析
根据上表z/b、ES1/ES2及pz计算值,以ES1/ES2为横坐标,pz/ p0为纵坐标,对各计算方法所得结果及其平均值进行对比,如图1、图2所示。
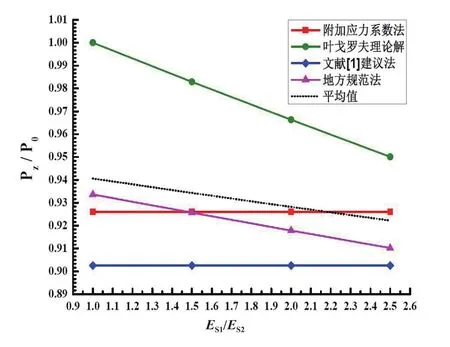
图1 ES1/ES2~ pz / p0计算值对比图(z / b=0.25)Fig.1 ES1/ES2~ pz / p0 calculated values comparison(z / b=0.25)

图2 ES1/ES2~ pz / p0计算值对比图(z / b=0.50)Fig.2 ES1/ES2~ pz / p0 calculated values comparison(z / b =0.50)
由图1、图2可见,当1≤ES1/ES2<3时:
(1)叶戈罗夫理论解计算所得软弱下卧层顶附加应力pz最大,安全度最高,但过于保守;根据高大钊建议,取压缩模量比等于3的扩散角计算所得pz最小,安全度最低。
(2)z/b相同的情况下,叶戈罗夫理论解和地方规范法计算所得pz值随ES1/ES2的增大而减小,即随着ES1/ES2的增大,扩散作用增强。而附加应力系数法和高大钊建议方法计算所得pz值保持不变。
(3)ES1/ES2一定的情况下,pz随 z/ b值(z/b≤0.5)的增大而减小,即z/b≤0.5情况下,压缩模量比相同时,基础底面至软弱下卧层顶面距离z越大,扩散作用越强。
(4)当ES1/ES2≤2时,附加应力系数法和地方规范法计算所得pz值接近平均值,且两者相差不大;当2<ES1/ES2<3时,附加应力系数法和地方规范法计算所得pz值差异增大。总体上,与地方规范法相比,附加应力系数法稍偏安全。
3 结语
对于江南地区,软弱下卧层验算时,1≤ES1/ES2<3的情况较为常见,此时可认为上下土层压缩模量差异较小。综合比较,叶戈罗夫理论解和高大钊建议方法所得结果偏差较大;附加应力系数法和地方规范法计算结果相对合理,但考虑到附加应力法理论成熟、应用广泛且在造价可接受的范围内稍偏安全,建议优先采用附加应力系数法;同时对于江南地区而言,通过试验等途径获得符合地区土性的地基压力扩散角经验值,也是值得尝试探索的方法。
高大钊,2010. 岩土工程勘察与设计—岩土工程疑难问题答疑笔记整理之二[M]. 北京:人民交通出版社.
住房与城乡建设部,国家质量监督检验检疫总局,2011. 建筑地基基础设计规范(GBT50007-2011)[S]. 北京:中国建筑工业出版社.
隋艳革,杜栩,张朝庆,2001. 软弱下卧层承载力验算通用计算方法理论模式的剖析[J]. 林业科技情报,35(1):1-2.
余晓东,2008. 软弱下卧层的验算方法及对浅基础不良影响的探讨[J]. 硅谷,(1):179.
孔祥国,2004. 软弱下卧层的验算方法探讨[J]. 岩土工程技术,18(3):141-143.
张启兵,2008. 软弱下卧层地基承载力验算中常见的几个问题分析[J]. 安徽建筑,(3):100-101.
张高峰,2007. 验算软弱下卧层强度时应注意的问题[J]. 岩土工程技术,21(4):199-201.
茅卫兵,姚恒,陈蕾,等,2007. 地基软弱下卧层验算中有关问题的探讨[J]. 江苏建筑,(6):23-25.
张晓范,吕志忠,姜继红,等,2007. 关于地基压力扩散角θ的取值方法的探讨[J]. 沈阳大学学报,19(2):103-104.
浙江省建设厅,2003. 浙江省建筑地基基础设计规范(DB33 1001-2003)[S]. 浙江:浙江大学出版社.
天津市城乡建设委员会,2011. 天津市岩土工程技术规范(DB 29-20-2000)[S]. 北京:中国建筑工业出版社.
Discussion on Calculation Methods of Additional Stress on Top Surface of Weak Substratum under Natural Foundation
SUN Jun
(Changzhou City Planning and Design Institute, Changzhou 213000)
The key point of weak underlying layer examination under natural foundation is the calculation of additional stress on top surface of weak substratum. At present, the additional stress coefficient calculation is not clear and defined if 1≤ES1/ES2<3 in national standards, so this paper adopts two methods to calculate the stress coefficient as additional stress coefficient method and expansion angle of subgrade pressure methods (including Yegorov theoretical solution method, suggestion method by GAO Dazhao and local standards), meanwhile considers changes of compression modulus ratio and depth, and analyzes and compares the calculating results from different calculation methods. The suggestions of additional stress calculation in the case of 1≤ES1/ES2<3 is provided.
Weak substratum; Compression modulus ratio; Additional stress coefficient; Expansion angle of subgrade pressure
A
1007-1903(2017)04-0083-04
10.3969/j.issn.1007-1903.2017.04.016
孙君(1983- ),男,硕士,高工,主要从事岩土工程勘察相关工作。E-mail:sunjun_czpad@163.com
