两类图的符号控制数

闫云娟，徐保根，冯大一

（华东交通大学理学院，江西 南昌330013）

两类图的符号控制数

闫云娟，徐保根，冯大一

（华东交通大学理学院，江西 南昌330013）

设图 G=（V，E）为一个图，一个双值函数如果对任意的 v∈V,均有 f（N［v］）≥1成立，则称 f为图 G 的一个符号控制函数,图 G 的符号控制数定义为 γs（G）＝min｛f（V）｜f为图 G 的一个符号控制函数｝。C（n，m）=CnPm表示Pm的一个端点与Cn中的一个点粘接（重合）而成的图；C（n，m，n）=CnPmCn表示Pm的两个端点分别粘接一个Cn而成的图。 文章确定了 C（n，m）和 C（n，m，n）的符号控制数。

图；符号控制函数；符号控制数

1 相关定义及推论

设图G=（V，E）,对于任意顶点v∈V,在G中与v点相邻的所有顶点的集合称为v在图G中的开邻域，记作 NG（v）=｛u｜uv∈E（G）｝，v 点在图 G 中的闭邻域记为 NG［v］＝NG（v）∪｛v｝。 顶点 v 在 G 中的度是指 v 在 G中邻点的个数，记作，不引混乱时，分别简记为 N（v），N［v］和 d［v］。 Cn和 Pn分别表示 n 阶圈和路。

对于图 G=（V，E），定义一个函数 f：V→R 和 G 的一个子集

J E Dunbar[1]等在1995年首次提出了图的符号控制的概念，这很快受到了学者们的广泛关注。

定义 1[2-4]设图 G=（V，E）为一个图，一个双值函数 f：V→｛1，1｝，如果对任意的 v∈V，均有 f（N［v］）≥1成立，则称f为图G的一个符号控制函数，图G的符号控制数定义为：γs（G）＝min｛f（V）｜f为图G的一个符号控制函数｝，并将使得γs（G）＝f（V）的符号控制函数称f为图G的一个最小符号控制函数。

引理 1[5-7]设 f为图 G 的一个符号控制函数，v∈V,当 d（v）为奇数时 f（N［v］）≥2，当 d（v）为偶数时 f（N［v］）≥1。

引理 2[8-9]设 n≥3，圈 Cn的最小控制数

定义2 由Pm的一个端点与Cn中的一个点粘接（重合）而成的图形称为气球图记为C（n，m）=CnPm，Pm与Cn的粘接点记为v2（um）；在Cn上从v1开始逆时针编号，在Pm上从u1开始从左到右编号。

定义3 由Pm的两个端点分别粘接一个Cn而成的图形称为哑铃图记为C （n，m，n）=CnPmCn，左侧Cn和 Pm的粘接点记为v2（w1），右侧 Cn和 Pm的粘接点记为 u2（wm）；在左侧 Cn上从 v1开始逆时针编号，在右侧Cn上u1从开始顺时针编号，在Pm上从w1开始从左到右编号。

2 主要结论及证明

证明 设圈Cn和路Pm的粘接点为v2=um，圈Cn上共有n个点，路Pm上有m个点；设f为图G1的一个最小符号控制函数，则 γs（G）=f（V），显然 f（u1）=f（u2）=1，否则与 f为图 G1的一个最小符号控制函数矛盾。

1） 当 m=3t时。

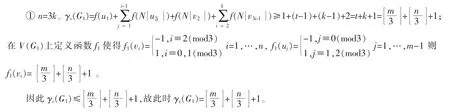
② n＝3k+1 。 因为 d（v2）=3，必有 f（N v2[]）≥2，故 v2闭邻域内对应的最小符号控制函数值为“-1”的点至多只有一个，分以下两种情况讨论：

情况2 若v2闭邻域内标号为“-1”的点不在圈上。则必有f（v2）=1。

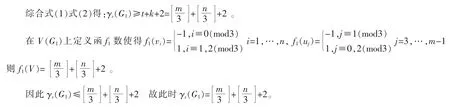
③n＝3k+2。由②同理：

情况 1 不妨设 f（vn）＝f（v1）=f（v2）=1 。

证明 由Pm的两个端点分别粘接一个Cn而成的图形称为哑铃图记为C（n，m，n）＝CnPmCn，左侧Cn和Pm的粘接点记为 v2（w1），右侧 Cn和 Pm的粘接点记为设 f为图 G2的一个最小符号控制函数，则 γs（G）=f（V）。

1） 当 n=3l时 。

[1]DUNBAR J E，HEDETNIEMI S T，HENNING M A，et al.Signed domination in graphs[J].J Shanghai Univ，2006（10）：4-8.

[2]BONDY J A，MURTY V S R.Graph theory with applications[M].Amsterdam：Elsevier，1976.

[3]HAYNES T W，HEDETNIEMI S T，SLATER P J.Signed，domination in graphs[M].New york：Marcel Dekker Inc，1998.

[4]徐保根.图的控制理论[M].北京：科学出版社，2008.

[5]徐保根.图的控制与染色理论[M].武汉：华中科技大学出版社，2013.

[6]徐保根.关于图的符号星控制数[J].华东交通大学学报，2004，21（4）：116-118.

[7]徐保根.两类图的符号星控制数[J].华东交通大学学报，2005，22（4）：146-148.

[8]徐保根.偶图符号控制数的下界[J].华东交通大学学报，2014，31（6）：93-95.

[9]徐荣贵，孔祥阳，徐保根.两类特殊图的控制数[J].江西科学，2015，33（1）：57-58.

On Signed Domination Numbers for Two Classes of Graphs

Yan Yunjuan，Xu Baogen，Feng Dayi
（College of Science,East China Jiaotong University,Nanchang 330013,China）

LetG=（V，E） be a graph,a functionf：V→{1，－1}is said to be a signed dominating function(SDF);when S⊆V,there is the followingf（S）holds for all v∈V,the signed domination number is γs（G）＝min ｛f （V）｜f is an SDF of G}.In this paper,the signed domination problem for two classes of special graphs is researched and the signed domination numbers ofC（n，m）=CnPmandC（n，m，n）=CnPmCnare obtained.

graph;signed dominating function;signed domination number

（责任编辑 姜红贵）

O157.5

A

1005-0523（2017）06-0109-07

2017－06－22

国家自然科学基金（11361024）；江西省高校科技落地计划项目（KJLD12067）；江西省自然科学基金项目（20171BAB201009）

闫云娟（1977—），女，讲师，研究方向为图与网络。