使用混合代理模型的自主式水下航行器藕节壳体多目标优化

何衍儒, 宋保维, 曹永辉

(西北工业大学 航海学院, 陕西 西安, 710072)

使用混合代理模型的自主式水下航行器藕节壳体多目标优化

何衍儒, 宋保维, 曹永辉

(西北工业大学 航海学院, 陕西 西安, 710072)

针对已有藕节壳体结构优化设计均为简化模型, 且没有对内部有效体积进行分析的问题, 文中使用非支配排序遗传算法(NSGA-II)和由径向基函数、支持向量回归函数、Kriging函数构建的混合代理模型,对自主式水下航行器(AUV)的切弧连接藕节壳体和环肋加强藕节耐压壳体进行了浮重比和内部有效体积的多目标优化, UG二次开发程序实现了藕节壳体的参数化建模, 并在满足强度和稳定性要求的前提下, 准确有效地获得该多目标优化问题的Pareto前沿, 可为AUV壳体优化设计提供参考。

自主式水下航行器(AUV); 藕节壳体; 多目标优化; 混合代理模型; NSGA-II

0 引言

自主式水下航行器(automatic underwater vehicle, AUV)近年来广泛应用在科学、商业和军事等领域。传统水下航行器的设计往往依靠圆柱型壳体的经验公式, 构造环肋加强圆柱壳体。然而,随着水下航行器航行深度的增加, 环肋加强壳体满足强度和稳定性条件的压力逐渐增大[1-3]。虽然先进的复合材料可以提高水下航行器壳体结构的性能, 但是生产成本也大大增加。一种有效的解决方案是在设计阶段, 利用计算机辅助工程(computer aided engineering, CAE)改变壳体结构的形状, 从而提高强度和稳定性。

从几何的角度来看, 球形壳体是最佳承压形式, 藕节壳体同时具有球壳和圆柱壳两者的优点,弥补了常规压力壳的缺陷。Liang等[4]采用扩展的内部罚函数法, 研究了藕节耐压壳体的优化设计;伍莉等[5-6]采用有限元方法, 研究了大深度潜水器的三藕节切弧连接耐压壳体的强度和稳定性性能, 提出该结构的材料线性和材料非线性强度经验公式, 并考虑材料非线性初始缺陷的影响, 提出其稳定性经验公式; 宋保维等[7]利用有限元软件对二藕节切弧连接耐压壳体在不同厚度、不同切弧角下的强度和稳定性进行了分析, 给出了最大应力和稳定性系数随厚度和切弧角的变化规律;苟鹏等[8]建立了Kriging代理模型, 对不同工作深度下的深潜多球交接耐压壳进行了结构的优化研究; 董华超等[9]使用Kriging代理模型和一种多起点全局优化方法, 对环肋加强藕节球壳进行了优化。上述研究均是对2到3个藕节球壳进行分析, 设计参数较少, 且并没有应用到具体的水下航行器。

基于代理模型的全局优化算法已经广泛用于解决需要长时间计算模拟的黑箱问题。代理模型[10-12]优化过程包括 3个步骤: 1) 选择采样点;2) 构造替代模型; 3) 优化并加入新的采样点。基于多个子代理模型的混合代理模型[13-17]方法, 可以降低优化问题的差异性和不可预测性, 同时提高模型的精确度。相对于传统的环肋加强圆柱壳体, 藕节壳体结构虽然在强度和稳定性满足要求的前提下浮重比有了大幅提高, 即加强了负载能力, 但是内部可用体积有一定的下降。根据这个问题, 文中研究了基于混合代理模型的 AUV藕节壳体结构的多目标优化, 可以在满足强度和稳定性要求的前提下, 准确有效地获得该多目标优化问题的Pareto前沿, 对于解决带约束的非线性多目标优化问题具有较好的工程参考价值。

1 混合代理模型

带约束的黑箱全局优化问题可以定义为

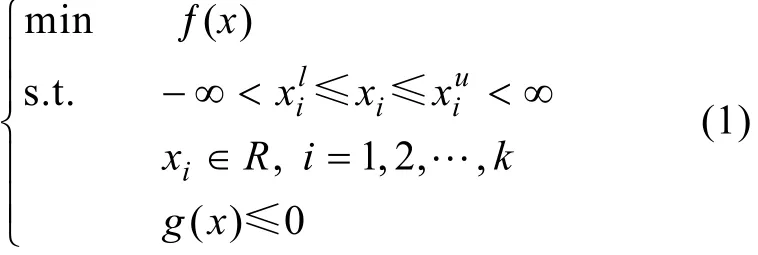
单个代理模型对不同优化问题具有很大差异性和不可预测性, 这给工程优化带来了一定的风险性。针对这个问题, 提出了基于多个子代理模型构造混合代理模型的方法, 可降低这些风险,同时提高模型的精确度。混合代理模型为

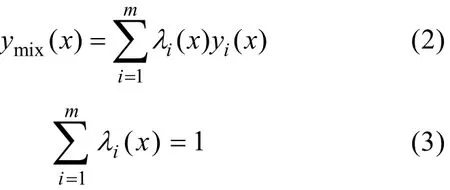
式中: x为设计变量; ymix为混合代理模型的响应值; m为混合代理模型包含的子代理模型个数;yi( x)和 λi( x )分别代表第i个子代理模型和相对应的权重系数, 权重系数之和等于1。

支持向量回归(support vector regression, SVR)方法[18]、径向基函数(radial basis functions, RBF)方法[19]和克里格(Kriging)方法[20]是工程中应用比较广泛的代理模型方法, 文中选取这 3种方法来构造混合代理模型。

1.1 SVR代理模型

SVR方法支持向量机在回归学习上的应用,该方法可以简要概述如下。给定一组训练样本｛(x1, y1) ,(x2, y2),… ,(xn, yn)｝, 其中每一个xi∈R表示样本点的输入, 并且有一个相对应的目标值yi∈R, 对应训练样本的数目。SVR估计函数的一般形式为

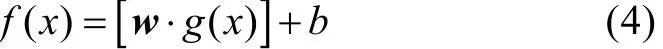
式中: w是权重向量;g( x)是从低维输入空间到高维特征空间的一组非线性变换;b是偏差。

SVR非线性拟合函数

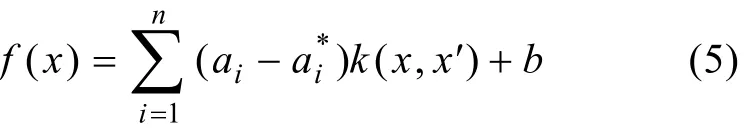
1.2 RBF代理模型

RBF是以径向函数为基函数通过线性叠加构造的模型, 基本形式

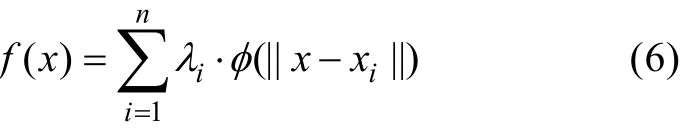
式中: n是采样点数; | |x - xi||是x与第i个采样点xi在设计空间的距离; φ(·)为基函数; λi是基函数在第i个采样点的未知加权因子。

经过测试, 文中选取3次函数作为基函数的RBF模型。

1.3 Kriging代理模型

Kriging是一种使用广义高斯方程作为基函数的特殊形式径向基函数插值方法, 该方法是根据样本空间的位置不同与样本间相互关联程度而不同, 对每个样本赋予不同的权进行滑动加权平均, 用来估计未知空间的样本信息。Kriging模型的预测响应值和均方误差(mean square error,MSE)可以表示

1.4 权重系数计算

构建混合代理模型的核心是确定子代理模型的权重系数 λi(x)。留一交叉验证法(leave one out, LOO)可以有效地获得子代理模型的特征值。首先取出 1个采样点, 用剩下的采样点和他们相对应的目标函数值和约束值构建代理模型, 然后用重建的代理模型重新预测取出采样点的目标函数值和约束值, 最后可以得到每个代理模型对每个采样点的预测值。文中选取相关系数(correlation coefficient, CC)、均方根误差(root mean square error, RMSE)和最大绝对误差(maximum absolute error, MAE)作为代理模型的特征值。其中

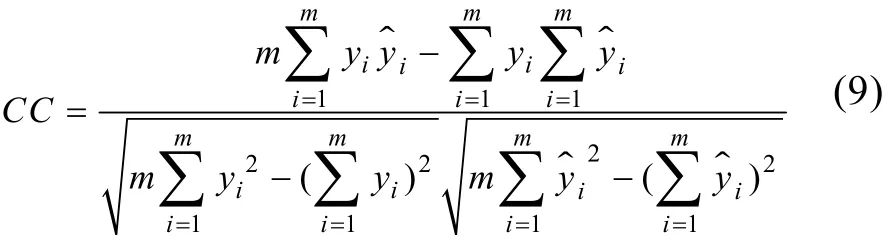
相关系数越高(接近1), 均方根误差和最大绝对误差越低(接近0), 说明代理模型的准确性越好。

D-S证据理论[21](dempster-shafer theory, DST)是一种由Dempster于1967年提出的不确定性推理方法, 该理论允许把整个问题和证据分解为若干个子问题、子证据, 在对子问题、子证据做出相应地处理后, 利用Dempster组合规则可以得到整个问题的解, 组合规则的形式为

2 自适应罚函数

文中对藕节球壳体进行强度和稳定性分析,所以把最大等效应力和屈曲系数被设定为约束条件。现有的文献中已经提出了许多不同的约束处理方法[22-24], 常见的包括以下几种: 保护可行解、罚函数、分离可行解和不可行解决以及混合方法。Woldesenbet等[25]提出了基于平衡可行解和不可行解的自适应惩罚函数方法来解决带约束的多目标优化问题。如果当前种群中的可行解较少, 则使用较大的惩罚因子将解推向可行区域,否则使用较小的惩罚因子。自适应罚函数包含 2个部分: 距离和自适应惩罚。可以表示为

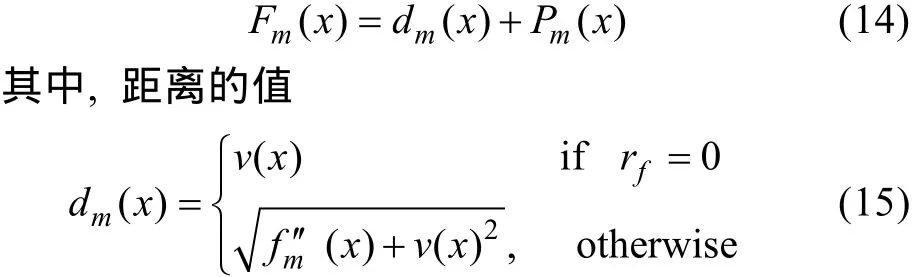
其中: v( x)是整体的约束冲突; rf是种群中可行解所占的比例; fm'' ( x)是第m个目标的归一化目标函数值, 且

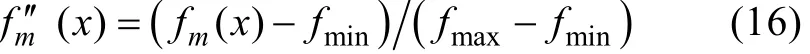
式中, fmax和 fmin是相应目标函数当前的最大值和最小值。

3 混合代理模型优化算法

Deb等[26]提出的非支配排序遗传算法(nondominated sorting genetic algorithm II, NSGA-II)是一种进化优化算法, 该方法不仅能获得均匀分布的Pareto最优解集, 而且有很强的稳定性和适应性, 是广泛使用的多目标算法。

文中提出的优化框架是基于混合代理模型和NSGA-II的全局优化策略(具体步骤见图1)。

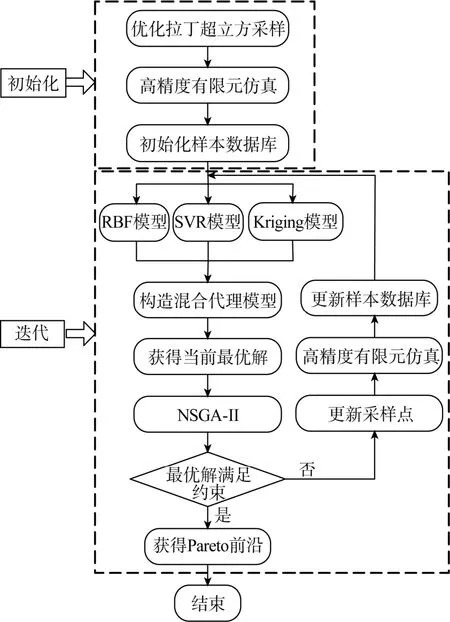
图1 基于混合代理模型和NSGA-II的全局优化流程Fig. 1 Flowchart of global optimization process based on mixture surrogate model and non-dominated sorting genetic algorithm II(NSGA-II)

每一次迭代过程中通过 NSGA-II补充一组采样点, 并对这一组采样点进行高精度有限元仿真分析, 将分析结果加入到样本数据库, 从而更新混合代理模型。以此往复求得Pareto最优解。基于混合代理模型和NSGA-II的全局优化策略总结如下。1) 试验设计: 使用优化拉丁超立方采样方法在整个设计空间生成 N个采样点。2) 对生成的N个采样点进行有限元分析, 并将结果存储在样本中。3) 根据计算值对所有样本进行排序。4) 构建混合代理模型的目标约束函数, 样品值使用真实的有限元分析计算值。5) 通过NSGA-II方法获得下一代采样点。6) 对新的采样点进行有限元分析。7) 将新的采样点计算值添加到样本数据库并进行更新, 获得Pareto前沿。8) 重复步骤4)到7), 直到Pareto前沿几乎不变。

4 AUV藕节球壳体多目标优化

4.1 优化模型

常见的藕节壳体包括2种结构形式: 切弧连接和环肋加强。图 2显示了2种藕节壳体的截面几何参数。图中: R=324 mm为AUV平行中段半径值; Re是有效半径; L是相邻藕节肋骨的间距;t是壳体厚度; r是圆角半径; x1, x2, x3, x4为环肋加强藕节壳体的肋骨截面参数; α为回转角度。文中, AUV平行中段的总长L为1 500 mm, 藕节肋骨数为n。肋骨数为8的AUV藕节耐压壳体参数化模型如图3所示。

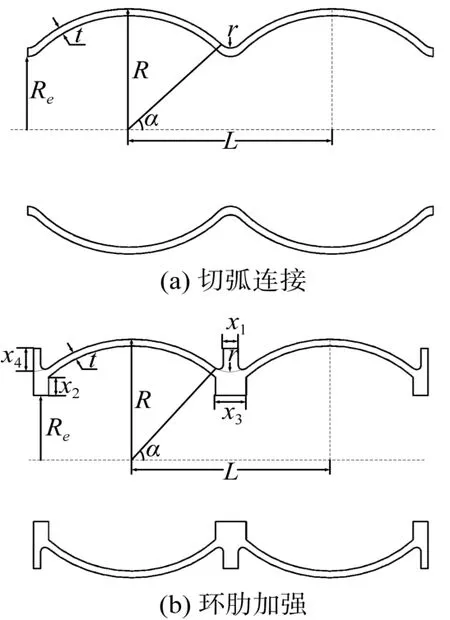
图2 藕节壳体几何参数Fig. 2 Geometry parameters of multiple intersecting spheres

图3 藕节壳体模型Fig. 3 Model of multiple intersecting spheres

AUV切弧连接和环肋加强藕节球壳体的多目标优化问题可以分别定义如下

式中: 切弧连接藕节壳体的设计变量为t和α;环肋加强藕节壳体的设计变量为t, x1, x2, x3,x4; B/ G为浮重比; Ve为壳体内部的有效体积;Re为壳体结构的有效半径; n为藕节肋骨的数目; t为壳体厚度; α为旋转角度; σmax为壳体的最大等效应力; bf为壳体的屈曲系数; 等效应力安全因子γ1=1.2; 屈曲系数安全因子γ2=1.2;x1, x2, x3, x4为环肋加强藕节壳体的结构参数。

文中材料选用钛合金, 屈服极限σs=930 MPa, 杨氏模量E=96 GPa, 泊松比μ=0.36, 密度ρ=4.62×103kg/m3, 耐压壳体的最大下潜深度为1 000 m, 此时壳体所受外压载荷P=10 MPa。有限元分析中, 端面轴向载荷的值

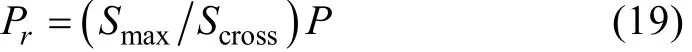
式中: Smax为最大横截面积; Scross为壳体端面面积。

可以通过满足几何约束来确定旋转角度α的初始范围。然后使用随机抽样的方法选取设计点, 并对其进行有限元分析。考虑等效应力约束和屈曲系数约束, 可以获得设计变量 x1, x2, x3, x4的初始范围。具体参数如式(17)和(18)所示。

经过初步的参数化建模和有限元分析计算,对壳体进行了结构受力分析和失稳分析。当藕节数 n ≥ 9 时, 切弧连接藕节壳体的设计变量区间变得很窄, 浮重比很低, Pareto前沿很窄; 当n≤ 5 时, 切弧连接藕节壳体的内部有效体积很小; 当 n ≥ 1 1时, 环肋加强藕节壳体的设计变量区间变得很窄, 浮重比很低, Pareto前沿很窄; 当n≤ 7 时, 环肋加强藕节壳体的内部有效体积很小。综上所述, 考虑到实际应用问题, 文中对藕节数 n = 6 , n = 7 , n =8的切弧连接藕节壳体以及藕节数 n = 8 , n = 9 ,n =10的环肋加强藕节壳体进行浮重比和内部有效体积的多目标优化设计。

4.2 计算结果与分析

初始样本点数目选为20v, v表示设计变量的数目。通过优化拉丁超立方采样方法构造初始样本点, 并对样本点进行高精度有限元分析, 获取结构的浮重比、内部有效体积、最大等效应力、屈曲系数, 形成初始样本数据库。文中, NSGA-II的代数设为500, 种群大小为30, 经过10次的迭代更新, 多目标优化问题的Pareto前沿基本不再发生变化, 考虑到计算成本, 可以停止迭代, 获得Pareto前沿。

1) 混合代理模型的准确性

混合代理模型的预测值是否精确对后续的多目标优化问题有着显著影响, 因此, 有必要对混合代理模型的精确性进行分析。针对藕节数n=8的环肋加强藕节壳体, 根据第2节所述, 通过优化拉丁超立方采样方法获得 100组采样点, 对最大等效应力和屈曲系数混合代理模型。此外,用拉丁超立方采样方法产生新的 20组采样点用作比较, 对新的采样点, 混合代理模型预测值与实际有限元分析的计算值对比见图4。可以发现,浮重比和内部有效体积的混合代理模型预测值与有限元计算值很接近, 说明代理模型精确度很高;相对而言, 最大等效应力和屈曲系数的代理模型精确度低了一些。为了验证混合代理模型的准确性, 采用CC, RMSE和MAE 3个指标来进行计算分析。此外, 分别单独使用SVR、RBF和Kriging来构造代理模型。浮重比( B / G)、内部有效体积Ve、最大等效应力σmax、屈曲系数bf的误差分析结果见表1。

根据误差系数计算, 相对于单个代理模型,混合代理模型的CC更高, RMSE和MAE更低,说明精确度更高, 因此选取混合代理模型进行下一步的优化。

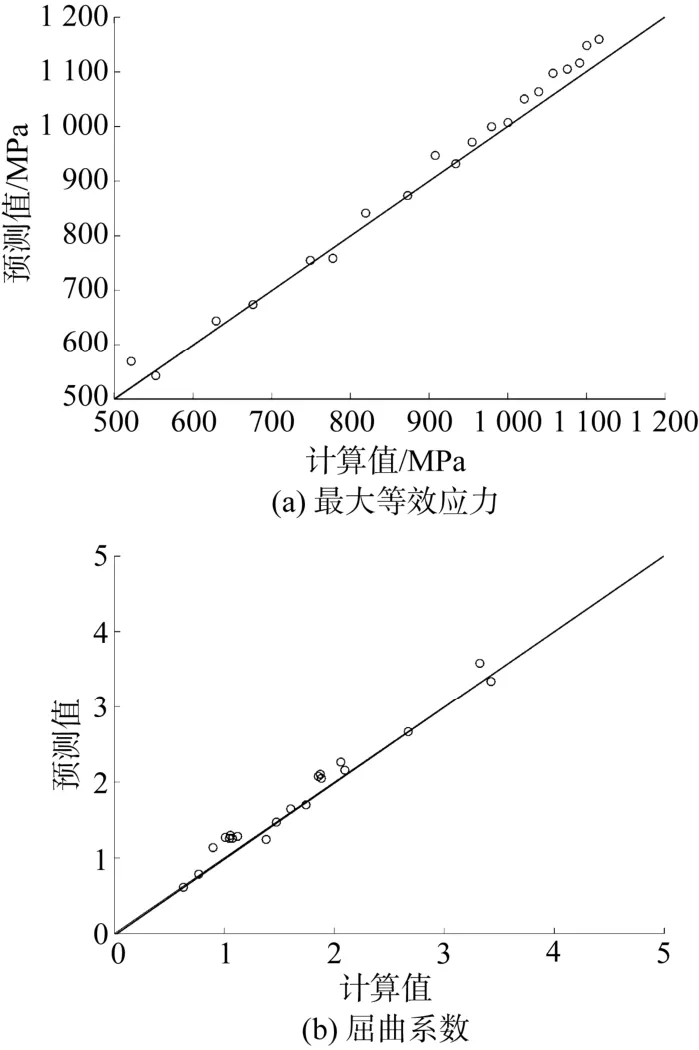
图4 代理模型预测值与有限元计算值对比图Fig. 4 Results comparison between surrogate model prediction and finite element analysis

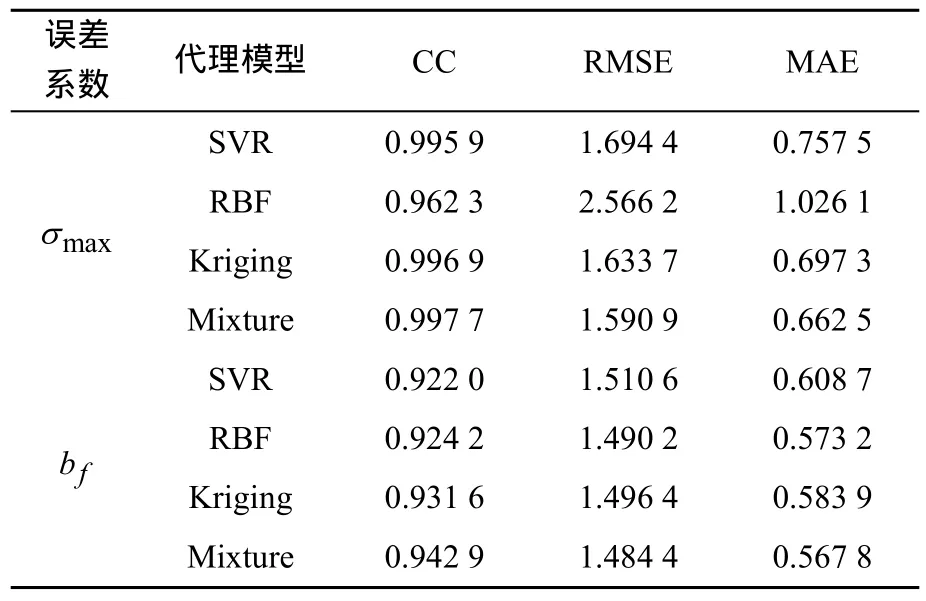
表1 误差系数分析结果Table 1 Results of error coefficient analysis

2) 切弧连接藕节壳体

藕节数 n=8时, 切弧连接藕节壳体的 Pareto前沿如图5所示。

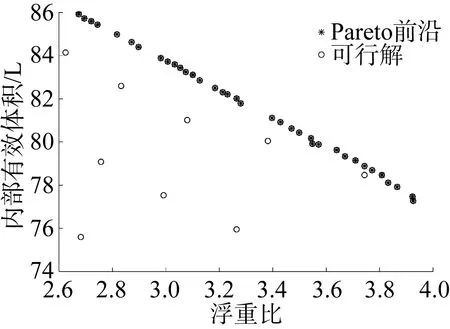
图5 n=8时切弧连接藕节壳体的Pareto前沿Fig. 5 Pareto front of tangent arc connective multiple intersecting spheres when n=8

当藕节数n=8时, 在构造切弧连接藕节壳体的最大等效应力、屈曲系数的混合代理模型过程中, RBF代理模型在构造壳体最大等效应力、屈曲系数的代理模型时体现了较高的准确性。

藕节数n=6, n=7, n=8的Pareto前沿如图6所示。其中, 当藕节数n=7时, Pareto前沿的跨度最大, 包含的可行解最多。随着藕节数的增加, 壳体的浮重比相对减小, 壳体的内部有效体积也随之增大。在相同的浮重比下, 藕节数越大, 内部的有效体积越大。

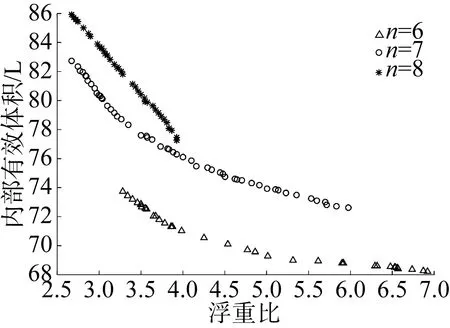
图6 n=6, 7, 8时切弧连接藕节壳体的Pareto前沿Fig. 6 Pareto front of tangent arc connective multipleintersecting spheres when n=6, 7 and 8

3) 环肋加强藕节壳体

藕节数 n=8时, 环肋加强藕节壳体的 Pareto前沿如图 7所示。此时, 在构造环肋加强藕节壳体的最大等效应力、屈曲系数的混合代理模型过程中, SVR代理模型体现了较高的准确性。

藕节数n=8, n=9, n=10的环肋加强藕节壳体Pareto前沿如图8所示。其中, 当藕节数为8时,Pareto前沿的跨度最小, 包含的可行解最少。随着藕节数的增加, 壳体的浮重比减小, 壳体的内部有效体积也随之变大。在相同的浮重比下, 藕节数越大, 壳体内部的有效体积越大。当藕节数n=8时, 切弧连接藕节壳体和环肋加强藕节壳体的Pareto前沿如图9所示。可以发现, 切弧连接藕节壳体的Pareto前沿较为宽广和平滑, 而环肋加强藕节壳体的Pareto前沿较为狭窄。相比于切弧连接藕节壳体, 环肋加强藕节壳体的浮重比有了显著的提升, 而内部有效体积也随之减小。当壳体以浮重比为主要优化目标时, 可以选用环肋加强藕节壳体, 当需要更多的内部有效体积时,切弧连接藕节壳体更加合适。

图7 n=8时环肋加强藕节壳体的Pareto前沿Fig. 7 Pareto front of ring-stiffened multiple intersecting spheres when n=8

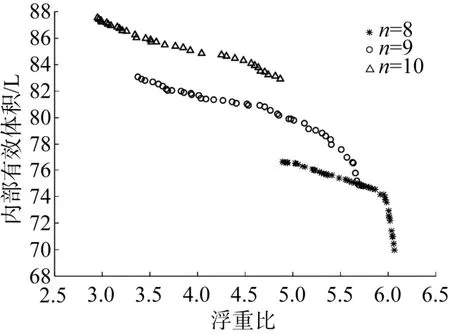
图8 n=8, 9, 10时环肋加强藕节壳体的Pareto前沿Fig. 8 Pareto front of ring-stiffened multiple intersecting spheres when n=8, 9 and 10

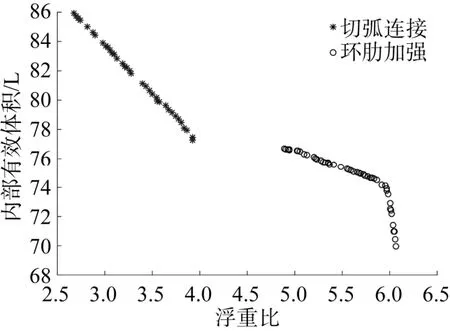
图9 n=8时2种藕节壳体所对应的Pareto前沿对比图Fig. 9 Pareto front comparison between two multiple intersecting spheres when n=8

5 结论

文中使用基于混合代理模型和NSGA-II的多目标优化方法, 实现了2种AUV藕节壳体的结构优化设计, 主要结论有: 1) 对相同藕节数和藕节形式的壳体, 在厚度不变的情况下, 回转角度α越大, 壳体强度和稳定性越好; 2) 对环肋加强藕节壳体而言, 加强环肋结构的横向参数x1和x3对壳体强度和稳定性的影响要远大于纵向参数x2和x4对壳体的影响; 3) 相比于切弧连接藕节壳体,环肋加强藕节壳体的浮重比更高, 内部有效体积相对较低。当以负载能力为主要优化目标时, 可以选用环肋加强藕节壳体; 当水下航行器需要更多的内部有效体积时, 切弧连接藕节壳体更加合适; 4) 随着藕节数目的增加, 壳体内部有效体积会增大, 但是壳体的浮重比也会减小。对同一种结构形式的藕节壳体而言, 当以负载能力为主要优化目标时, 可以选用较小的藕节数; 相反地,当水下航行器需要更多的内部有效体积时, 应该选用较大的藕节数; 5) 混合代理模型可以提高模型的精确度, 减少计算成本。基于混合代理模型和NSGA-II的全局优化策略可以有效快速地对藕节壳体进行优化。

文中对水下航行器藕节壳体优化问题具有一定的工程参考价值, 后续将进行试验验证分析。

[1] Alam K, Ray T, Anavatti S G. Design and Construction of an Autonomous Underwater Vehicle[J]. Neurocomputing,2014, 142(SI): 16-29.

[2] 朱崎峰, 宋保维, 李懿霖, 等. 基于CAD的自主式水下航行器几何模型参数化建模[J]. 机械设计, 2013, 30(9):58-62.Zhu Qi-feng, Song Bao-wei, Li Yi-Lin, et al. Parametric Modeling of Autonomous Underwater Vehicle Geometric Model Based on CAD[J]. Journal of Machine Design,2013, 30(9): 58-62.

[3] 董华超, 宋保维, 王鹏. 水下航行器壳体结构多目标优化设计研究[J]. 兵工学报, 2014, 35(3): 392-397.Dong Hua-chao, Song Bao-wei, Wang Peng. Multi-objective Optimal Design of Automatic Underwater Vehicle Shell Structure[J]. Acta Armamentarii, 2014, 35(3): 392- 397.

[4] Liang C C, Shiah S W, Jen C Y, et al. Optimum Design of Multiple Intersecting Spheres Deep-submerged Pressure Hull[J]. Ocean Engineering, 2004, 31(2): 177-199.

[5] 伍莉, 徐治平, 张涛, 等. 球形大深度潜水器耐压壳体优化设计[J]. 船舶力学, 2010, 14(5): 509-515.Wu Li, Xu Zhi-ping, Zhang Tao, et al. Optimum Design of Spherical Deep-submerged Pressure Hull[J]. Journal of Ship Mechanics, 2010, 14(5): 509-515.

[6] 伍莉, 陈爱志, 陈小宁, 等. 藕节形大深度潜水器耐压壳体强度与稳定性研究[J]. 船舶力学, 2010, 14(1): 74-83.Wu Li, Chen Ai-zhi, Chen Xiao-ning, et al. Strength and Stability Study of Multiple Intersecting Spheres for Great Deep-submerged Pressure Hull[J]. Journal of Ship Mechanics, 2010, 14 (1): 74-83.

[7] 宋保维, 成鹏飞, 曹永辉, 等. 藕节形耐压壳体强度与稳定性有限元分析[J]. 计算机仿真, 2013, 30(2): 38-41.Song Bao-wei, Cheng Peng-fei, Cao Yong-hui, et al. Strength and Stability Study of Multiple Intersecting Spheres for Pressure Hull[J]. Computer Simulation, 2013,30(2): 38-41.

[8] 苟鹏, 崔维成. 基于 Kriging 模型的深潜器多球交接耐压壳结构优化[J]. 船舶力学, 2009, 13(1): 100-106.Gou Peng, Cui Wei-cheng. Structural Optimization of Multiple Intersecting Spherical Pressure Hull Based on Kriging Model[J]. Journal of Ship Mechanics, 2009, 13(1):100-106.

[9] Dong H C, Song B, Wang P. Surrogate-Based Optimization for Autonomous Underwater Vehicle′s Shell Design[C]//Distributed Computing and Applications for Business Engineering and Science(DCABES)[C]//Cambridge, MA, USA: 2015 14th International Symposium on.IEEE, 2015: 393-397.

[10] Forrester A I J, Keane A J. Recent Advances in Surrogate-based Optimization[J]. Progress in Aerospace Sciences, 2009, 45(1): 50-79.

[11] Queipo N V, Haftka R T, Shyy W, et al. Surrogate-based Analysis and Optimization[J]. Progress in Aerospace Sciences, 2005, 41(1): 1-28.

[12] 韩忠华. Kriging模型及代理优化算法研究进展[J]. 航空学报, 2016, 37(1): 3197-3225.Han Zhong-hua. Kriging Surrogate Model and Its Application to Design Optimization: A Review of Recent Progress[J]. Acta Aeronautica et Astronautica Sinica, 2016,37(1): 3197-3225.

[13] Zhang J, Chowdhury S, Messac A. An Adaptive Hybrid Surrogate Model[J]. Structural and Multidisciplinary Optimization, 2012, 46(2): 223-238.

[14] Viana F A C, Haftka R T, Watson L T. Efficient Global Optimization Algorithm Assisted by Multiple Surrogate Techniques[J]. Journal of Global Optimization, 2013, 56(2): 669-689.

[15] 解欢, 杨岳, 童林军, 等. 基于混合代理模型的高速轨道车辆悬挂参数多目标优化[J]. 铁道科学与工程学报,2016, 13(10): 2056-2063.Xie Huan, Yang Yue, Tong Lin-jun, et al. Multi-objective Optimization of the Suspension Parameters for High Speed Rall Vehicle Based Ona Hybrid Surrogate Model[J].Journal of Rallway Science and Engineering, 2016, 13(10):2056-2063.

[16] 李召, 王大志, 时统宇, 等. 基于熵权与混合代理模型的永磁驱动器的优化设计[J]. 电机与控制学报, 2016,20(6): 102-108.Li Zhao, Wang Da-zhi, Shi Tong-yu, et al. Optimization Design for Permanent Magnet Drive Based on Entropyweight and Hybrid Surrogate Model[J]. Electric Machines and Control, 2016, 20(6):102-108.

[17] Müller J, Piché R. Mixture Surrogate Models Based on Dempster-Shafer Theory for Global Optimization Problems[J].Journal of Global Optimization, 2011, 51(1): 79-104.

[18] Yang H, Chan L, King I. Support Vector Machine Regression for Volatile Stock Market Prediction[C]//International Conference on Intelligent Data Engineering and Automated Learning. Berlin: Springer-Verlag, 2002: 391-396.

[19] Sun G, Li G, Gong Z, et al. Radial Basis Functional Model for Multi-objective Sheet Metal Forming Optimization[J].Engineering Optimization, 2011, 43(12): 1351-1366.

[20] Sun C, Song B, Wang P. Parametric Geometric Model and Shape Optimization of an Underwater Glider with Blended-wing-body[J]. International Journal of Naval Architecture and Ocean Engineering, 2015, 7(6): 995-1006.

[21] Sentz K, Ferson S. Combination of Evidence in Dempster-shafer Theory[M]. Albuquerque: Sandia National Laboratories, 2002.

[22] Qu B Y, Suganthan P N. Constrained Multi-objective Optimization Algorithm with an Ensemble of Constraint Handling Methods[J]. Engineering Optimization, 2011, 43(4): 403-416.

[23] Fonseca C M, Fleming P J. Multiobjective Optimization and Multiple Constraint Handling with Evolutionary Algorithms. I. A unified formulation[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part A: Systems and Humans, 1998, 28(1): 26-37.

[24] Qu B Y, Suganthan P N. Constrained Multi-objective Optimization Algorithm with Diversity Enhanced Differential Evolution[C]//Evolutionary Computation(CEC). Barcelona, Spain: IEEE, 2010: 1-5.

[25] Woldesenbet Y G, Yen G G, Tessema B G. Constraint Handling in Multiobjective Evolutionary Optimization[J].IEEE Transactions on Evolutionary Computation, 2009,13(3): 514-525.

[26] Deb K, Pratap A, Agarwal S, et al. A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II[J]. IEEE Transons on Evolutionary Computation, 2002, 6(2): 182-197.

Mixture Surrogate Model Based Structural Optimization Design of Multiple Intersecting Spheres for Automatic Undersea Vehicle

HE Yan-ru, SONG Bao-wei, CAO Yong-hui
(School of Marine Science and Technology, Northwestern Polytechnical University, Xi′an 710072, China)

To solve the problem that the existing structural optimization designs of multiple intersecting spheres are simplified models and are lack of internal effective volume analysis, this paper uses the non-dominated sorting genetic algorithm II(NSGA-II) and the mixture surrogate model constructed by radial basis function, support vector regression function and Kriging function to perform multi-objective optimization of the tangent arc connective and ring-stiffened multiple intersecting spheres of an autonomous undersea vehicle(AUV) in terms of the buoyancy-weight ratio and the internal effective volume of the spheres. Parametric modeling of the two multiple intersecting spheres are implemented using UG secondary development. The Pareto front of this multi-objective optimization problem is obtained under the constraint of satisfying maximum equivalent stress and bulking factor. This research may provide a reference for optimization design of AUV shell.

automatic undersea vehicle(AUV); multiple intersecting spheres; multi-objective optimization; mixture surrogate model; non-dominated sorting genetic algorithm II(NSGA-II)

U674.941; TJ630.2

A

2096-3920(2017)05-0410-08

10.11993/j.issn.2096-3920.2017.05.003

何衍儒，宋保维，曹永辉. 使用混合代理模型的自主式水下航行器藕节壳体多目标优化[J]. 水下无人系统学报, 2017, 25(5): 410-417.

2017-09-11;

2017-10-27.

国家自然科学基金资助项目(51375389).

何衍儒(1988-), 男, 在读博士, 主要研究方向为基于代理模型的水下航行器结构优化设计.

(责任编辑: 杨力军)