浅析培养中学生数学解题能力的策略

周洪波+++王喜红+++马旭

摘要：提高学生的解题能力是数学教学中的重要环节。学生的解题能力必须在教学的全过程中进行培养，在培养各种数学基本能力的同时逐步提高。本文结合案例提出了三个培养学生解题能力的策略：一是进行解题思维训练；二是掌握和运用数学思想方法；三是重视非智力因素，持续提高解题能力。

关键词：中学数学教学 解题能力 策略

目前中学生对数学学习是重视的，但效果却不是很理想，最突出的问题是，基本概念不清，基本技能不熟，数学解题能力薄弱，学习方法被动，集中暴露出来的问题是，数学能力不强。对此，有些教师采用了“题海战术”，在教学中只注重“就题论题”，抓具体解法的灌输，而忽视根本的数学能力的培养以及学习方法的指导。解题教学在数学教学中占有及其重要的地位，数学课对于解题教学，应予以高度重视，本文就如何提高中学生数学解题能力问题进行分析。帮助学生养成良好的数学学习习惯和数学学习方法，更灵活的分析问题、解决问题。

一、数学解题的意义

我国《普通高中数学课程标准》把“数学地提出、分析和解决（包括简单的实际问题）的能力”作为数学课程的主要目标，美国《学校数学课程的原则与标准》也把数学问题的解决作为各年级数学课程的重要组成部分，可见数学问题解决收到世界各国的广泛重视。研究解题的方法，掌握解题的规律，有助于发展数学思维能力，数学表达能力，提高数学学习的效率。

二、数学问题特点

数学问题是丰富多样的，它遍及数学学习的各个领域。无论是在学校生活中还是在日常生活中，到处都充满数学问题，这些问题既有魅力、又富有挑战性，他们有如下特点：

（一）数学问题的情境性

中学数学问题，往往与一定的具体情境相联系，联系具体的情景提出问题与解决问题，有助于激發学习动力，了解问题产生的背景，发展学生的数学引用能力。

（二）数学问题的挑战性

在数学学习中，有些数学问题的解决是没有常规的公式与套路，需要经过一定的努力与探究才能够解决。

（三）数学问题与数学思想方法的关联性

数学思想是人们探究数学自身规律，以及运用数学知识与规律解决有关问题的思维活动，它是数学的精髓和灵魂。数学方法是人们运用数学解决有关问题的手段和策略，是数学知识与解决问题相互联系的纽带，数学知识和数学方法相互紧密联系，方法以思想为指导，思想以方法为体现。数学解题要以一定的思想为指导，对数学思想的概括就形成了某种方法。

三、培养中学生数学解题能力的策略

解题是数学教师职业生活必不可少的部分，教师要指导学生解决形形色色的数学问题，在指导解决问题的过程中，帮助学生加深理解、温故知新、融会贯通，善于解题的教师能够使学生掌握解题的思路、方法，下面给出几点培养中学生解题能力的策略。

（一）进行系统的解题思维训练

1.审题思维训练，提高学生审题能力

阅读和仔细审题，是解题中的重要环节。解题方法，解题途径的选择和运用都有赖于仔细审题，有的教师要求学生至少审题三遍，直到题意清楚明白，是很有道理的，也是很有必要的。数学题目包括“已知”和“未知（结论）”两部分组成，对于较复杂的综合题，一般说来，题目中的已知和未知不全明显，或者条件比较隐蔽，就需要首先认真分析题目的隐蔽条件，因此，提高学生的审题能力，要注意训练学生善于分析隐蔽条件，转换已知和未知的审题思维。

例1 先后抛掷两枚均匀的正方体骰子（它们的六个面分别标有点数1、2、3、4、5、6），骰子朝上的面的点数分别为X、Y，则log2xY=1的概率为多少？

2.通过问题发散，训练学生思维的广阔性

通过一题多解、一题多变、一题多思培养学生发散思维品质，拓宽解题思路，提高解题的灵活性，同时也培养了学生综合运用数学知识的能力。一题多解训练，就是启发和引导学生从不同的角度、不同的思路，用不同的方法和不同的运算过程去分析、解答同一道数学题的练习活动。上这种课的主要目的有三条：一是为了充分调动学生思维的积极性，提高他们综合运用已学知识解答数学问题的技能技巧；二是为了锻炼学生思维的灵活性，促进他们长知识、长智慧；三是为了开阔学生的思路，引导学生灵活地掌握知识的纵横联系，培养和发挥学生的创造性。

（二）掌握数学思想方法是培养学生解题能力的关键

函数与方程思想、数形结合思想、分类讨论思想、转化与化归思想并称为高中数学四大数学思想，在解题过程中都是非常重要的思维方式，也是高中数学的主要培养目标。

1.数形结合思想

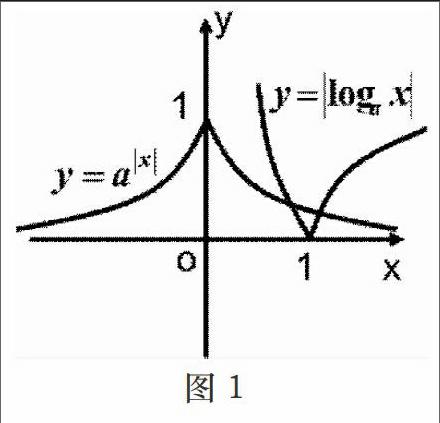
数形结合思想是非常重要的数学思想方法，可解决方程、不等式、函数问题，尤其在解析几何中显得尤为重要，其实质是将抽象的数学语言与直观的图形结合起来，使抽象思维和形象思维相互作用，通过对图形的处理，发挥直观对抽象的支柱作用，化难为易。

评析 本题很好的体现了数形结合的优越性，如果单纯的从数的观点来解题的话，得出交点个数是有一定难度的，但从形的角度出发，可以很直观的看出，平时解题时，一定要注意这种思想的应用。

例3 解决与几何有关的问题：已知α、b、c、d∈R+，证明：存在这样的三角形，它的三边等于

分析 题设的代数式比较复杂，略加化简可知，可以构造三角形使它的三边恰能用题设的代数式表示。

如图2所示，构作矩形。

2.分类讨论思想

分类讨论思想是中学数学教学中有着广泛应用的数学思想和方法，是一种重要的解题策略，教师在这解这类问题时一定引导学生将题目分析全面，确定讨论的对象和分类的标准，进行逐一讨论，归纳总结。

3.化归与转化思想

将未知问题化为已知，将复杂的问题化归为容易的、简单的问题，将整体问题分割为一些子问题去研究，都是化归思维的具体体现，教师要善于引导学生用合适的方法将问题转化，达到化繁为简，化生为熟.endprint

4.函数思想

函数思想是指用运动变化的观点来研究两个变量之间的相互联系与变化规律，并借助函数图像和性质去分析、解决问题的数学思想。在解题过程中会经常用到函数思想，例如：构造函数解决不等式问题，以此来研究函数的单调区间，单调性；运用函数思想解方程、比较大小、解決数列问题等等，在做题过程中灵活运用。

（三）重视非智力因素，持续提高解题能力

波利亚指出，“认为解题纯粹是一种智能活动是错误的，决心与情绪所起的作用很重要”。数学解题的过程是艰苦的，而将题目解出来的快乐是巨大的。数学解题不仅仅是智力因素在起作用，非智力因素的影响也是极其重要的。

首先，教师要调动学生学习数学的兴趣，兴趣是最好的老师，教师应该善于利用各种因素，调动学生的兴趣，吸引学生。一旦学习数学的兴趣被调动起来，他将会从常规的基本题，到极富挑战性的竞赛题，层层突破。

其次，鼓励学生要有信心，勇于克服困难，随着解答出来的题目越多，信心就会越强，信心越强，就越愿意去解题，逐步进入良性循环的轨道。

最后，教会学生解题要有耐心，有些学生，难题做不了，容易题不愿意做，所以解题能力得不到应有的提高，解数学题要沉得住气，在解题过程中。

四、结语

在数学学习中，要想提高解题能力，必须先学好数学基础知识，数学概念及公式、定理是解题的理论基础，是解题能力的关键所在。解题方法、解题途径的选择和运用都有赖于仔细审题，也是解题的重要环节，解题时要一题多解、一题多思、一题多做，灵活运用数学思想方法，同时，教师要注重非智力因素对解题能力的影响，培养学生数学学习的兴趣、信心和耐心，将智力因素和非智力因素相结合，才能够促进学生对知识技能的学习和掌握。数学的解题教学应该落实在解题的实践中，作为数学教师应该帮助学生掌握数学解题的基本策略，在培养学生数学能力的同时，教师自身的数学能力也得到提升，这就是教学相长的原理。

参考文献：

[1]曹才翰，章建跃.中数数学教学概论[M].北京：北京师范大学出版社，2012.

[2]许娟娟.数学教学中学生审题能力极其培养[J].教育与管理，2012，（24）.

[3]牟雪珍.巧用数形结合思想的解题探究[J].中学数学，2012，（12）.

[4]张平.略谈数学思想的渗透[J].吉林教育，2012，（12）.

[5]袁武平.高中数学教学中如何提升学生的解题能力[J].学周刊B版，2013，（03）.

[6]卢晓云.高中数学教学中学生解题能力的培养策略[J].考试周刊，2015，（87）.

（基金项目：2016 年宁夏回族自治区高等学校本科教学工程基于计算思维能力培养的师范生计算机基础课程教学改革研究 NXJG2016060；作者简介：[1]周洪波，硕士研究生，宁夏师范学院 数学与计算机科学学院，研究方向：数学学科教学；作者单位：宁夏师范学院 数学与计算机科学学院。 ）endprint