从解题错例中分析高中数学的难点

沈赫

摘要：在人类的历史长河以及社会生活中，数学是无处不在的，它是一门研究数量、结构、空间以及信息等概念的學科。数学的难点主要是为了考验学生思维反应能力。本文会以高中数学错题为例，分析高中数学难点，从而帮助学生找到攻破难点的方法。

关键词：高中数学 错题解析 难点攻破

高中数学由必修课程和选修课程组成，研究方向包括《集合与函数》《三角函数》《不等式》《数列》《复数》《排列、组合、二项式定理》《立体几何》《平面解析几何》等部分。只要学生有正确的学习方法以及认真的学习态度，攻克高中数学的难点完全不是问题。

一、知识掌握不透彻，容易混淆概念

高中数学的知识点较多，有的学生在学习的时候为了追求速度或者学习过后没有及时地复习，很容易把类似的知识点弄混，比如说这题：

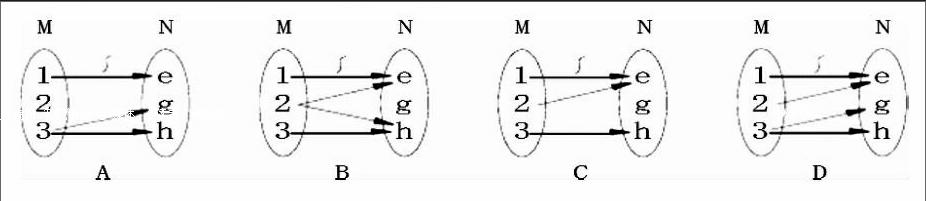
设M={1、2、3}，N={e、g、h}，从M至N的四种对应方式，其中是从M到N的映射是（ ）

映射的概念具体如下：

设A是一个集合、B也是一个集合，如果在此时为其选择一个相对应的关系f，那么此时A集合中对应的元素就为x，B集合中对应的元素就为y，因此我们说对应关系为f，得出的结论为A集合为B集合的映射。

函数的概念具体如下：

通常我们设定A为一个非空数集，B为一个非空数集，如根据一种法则f，那么A集合中的元素则对应为x，B集合中对应的元素为y，我们称这种集合为A集合到B集合的函数。（函数的本质是建立在两个非空数集上的特殊对应）

映射与函数的区别与联系：函数是建立在两个非空数集上的特殊对应；而映射是建立在两个任意集合上的特殊对应；函数是特殊的映射，是数集到数集的映射，映射是函数概念的扩展，映射不一定是函数，映射与函数都是特殊的对应。

映射与函数（特殊对应）的共同特点：（1）可以是“一对一”；（2）可以是“多对一”；（3）不能“一对多”；（4）A中不能有剩余元素；（5）B中可以有剩余元素。

映射的特点：（1）多元性：在映射中，非空集合A和非空集合B不仅可以是点集、图形集合外，还可以是数集等；（2）方向性：我们知道映射是具有一定的方向的，集合到集合中的映射是不尽相同的；（3）在映射中，A集合中所包含的元素都会在B集合中体现，我们称之为象，不要求B中的每一个元素都有原象；（4）唯一性：映射中集合A中的任一元素在集合B中的象都是唯一的；（5）一一映射是一种特殊的映射方向性。

上题答案应选C

本题是考查映射的概念和特点，应在完全掌握概念的基础上，灵活掌握变型题。俗话说：知道如何停止的人才知道如何加速。只有把基础打好了，才能为后续的题海战术做好充分的准备。

二、懒于画图帮助思考

在遇到有关函数单调性问题的时候，学生懒于画图思考，过于依赖自己的想象力。这样做实际上会延缓解题的速度，在考试的时候甚至会因为紧张而频频出错，比如说这题：

定义在R上的奇函数f（x）在（0，+∞）上是增函数，又f（-3）=0，则不等式x f（x） <0的解集为（）

易判断f（x）在（-∞，0）上的单调性及f（x）图像所过特殊点，作出f（x）草图，根据图像可解不等式。

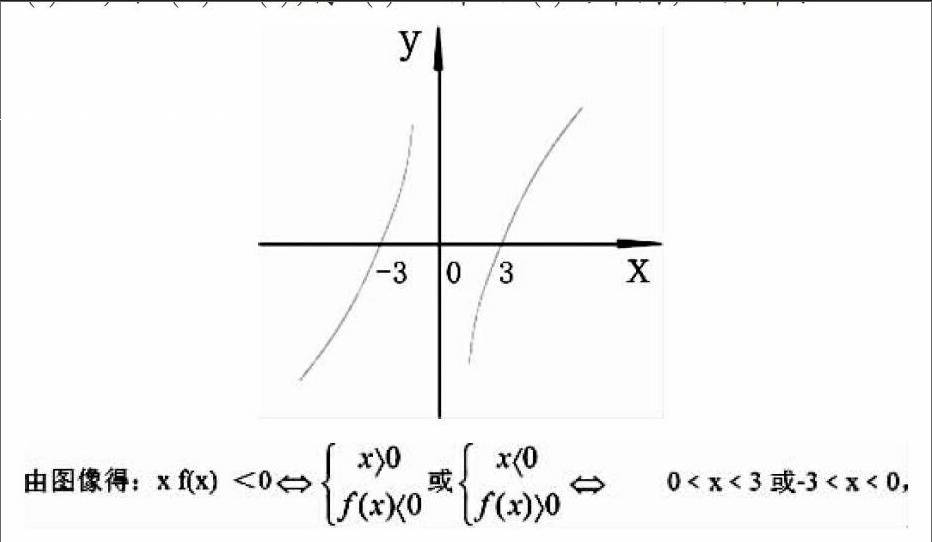
解：∵ f（x）在R上是奇函数，且f（x）在（0，+∞）上是增函数，∴ f（x）在（-∞，0）上也是增函数，由f（-3）=0，可得-f（3）=0，即f（3）=0，由f（-0）=-f（0），得f（0）=0作出f（x）的草图，如图所示：

本题考查函数奇偶性、单调性的综合应用，考查数形结合思想，灵活作出函数的草图是解题关键。

三、忽视题中隐含的关键条件

高中数学有些题目并不会把全部条件都体现在纸面上，而是要通过学生们的思考分析得出，此类题目就是要培养学生掌握挖掘题目实质的能力。比如说这题：

设α、β是方程x2-2kx+k+6的两个实根，则（β-1）2+（α-1）2的最小值是以下选项中的哪一个（ ）

A.8 B.不存在 C. -49/4 D.18

思路分析：在这个题中有且仅有一个是正确的答案，出题人设置了三个误导选项，我们通过正常的解题思路常常会得出α+β=2k， α*β=k+6

∴（α-1）2+（β-1）2=4*（k-3/4）2-49/4

其中存在学生一看到C选项时就选择了C，盲目的选择，这种选择就体现学生反向思维的缺乏。

∵原方程有两个实根α、β

∴△=4k2-4（k+6）≥0，解得k≤-2或k≥3，只有（B）正确。

四、理解偏差，出现错误

理解存在偏差，对问题的思考比较片面，没有考虑到特殊情况，进而导致解答出现漏洞，不能准确的计算出正确而全面的答案。比如说一下这题

求一条直线，该直线经过点（0，1），且该直线与某条抛物线相交，交点只有一个，这个抛物线是y2=2x。

错误解法为：设这条直线的方程式为y=kx+1，那么此时这条直线与y2=2x的焦点则为k2x2+（2k-2）x+1=0，解得k=1/2

根据解题思路我们可以看出，有三个地方是不对的；

首先，当设出直线的方程时，并没有考虑到若k为0的情况和没有斜率的状况，这种思维是不严谨的。

其次，审题后可以得知，我们要求的直线和y2=2x有交点，且只有一个，相交其实具有两种情况，一个是相交，另一个是相切。解题时并未考虑相切状况，存在纰漏。

最后，在解题时，通过将题目中的已知条件进行联立，进而得到一个方程，此时应对其判别式进行考虑，因此K不等于0。结合以上解题来看，并未考虑到种种状况，理解存在偏差，导致解题错误。

五、结语

总的来说，高中数学的难点就是要理解知识概念、了解题目内容、注意解题细节。这些要求对于每个高中生来说都是可以达到的，但又是难以坚持的。所以要攻克高中数学的难点需要持之以恒地做好学习上的每一个小细节，这才能取得长足的进步。

参考文献：

[1]宋胜利，刘立华.从解题错例中分析高中数学难点及认知偏差[J].高中数理化，2015，（12）.

[2]沈宏.高中数学易错题的分类与成因分析[J].中学数学月刊，2015，（12）.

[3]崔睿宁.高中数学错题分析与应对策略[J].考试周刊，2016，（A4）.

[4]王爱军.将错就错引悟促思——提高高中数学错题订正有效性的策略研究[J].上海中学数学，2016，（04）.

（作者单位：齐齐哈尔第八中学）endprint