泉州市工业经济与新兴产业互动关系研究——基于时变参数状态空间模型

(福建农林大学 金山学院,福建 福州 350002)

泉州市工业经济与新兴产业互动关系研究
——基于时变参数状态空间模型

陈 钦，王灿雄

(福建农林大学 金山学院,福建 福州 350002)

基于协整分析和状态空间模型，对2007年～2016年泉州市工业经济增长与新兴产业发展的关系进行实证研究。研究结果显示：从协整分析来看，泉州市工业经济增长与新兴产业发展之间存在着长期均衡关系，经济增长有58.15%的自动修复能力。根据时变参数，泉州工业增长对新兴产业增长的弹性系数动态震荡，在0.717～0.769之间徘徊。在实证分析的基础上对泉州市未来产业经济发展提出了建议。

工业经济；新兴产业；时变参数；状态空间模型

中国正处于工业化发展中期，传统的依靠三驾马车拉动的经济增长模式已不能满足现阶段中国经济发展的需要，迫切需要新的经济增长点来刺激其经济发展。传统产业向新兴产业的过渡、转型、升级是中国寻求新的经济增长点的必然要求。供给侧改革、大众创业、万众创新等的提出为新兴产业的发展注入了活力。泉州市工业经济的发展非常迅猛，自1995年以来，其GDP总量长年位居福建省地级市首位，大致占福建省GDP总量的1/4；2007年以来，随着海峡西岸经济区的确立，泉州市的GDP总量在浙江省、江西省、福建省以及广东省等所纳入核算的20个海峡西岸经济区地级市中依旧位居首位。“一路一带”倡议的提出，进一步推进了泉州市工业的发展，截至2016年，其GDP总值达到6 646.63亿圆，其中，工业产值3 903.85亿圆，工业产值占GDP总值的比重为58.73%，增速达7.4%。纺织鞋服、建筑建材、工艺制品、食品饮料、机械制造等作为泉州市的传统产业，曾经是其经济发展的支柱产业；但近年来泉州市的产业格局经历了一轮又一轮的重大变革，石油化工、电子信息、船舶制造、汽车制造、生物制药等新兴产业成长较快，成为引领泉州经济发展的先锋[1]。新兴产业在泉州市工业经济发展进程中到底扮演着什么样的角色？其对传统产业的发展将产生何种影响？如何制定未来泉州市新兴产业的发展规划？要分析与解决这些问题，可以从两个层面来解析泉州市的工业经济增长与新兴产业发展之间的互动关系。一方面，采用协整分析测度泉州市新兴产业产值与规模以上工业产值之间的短期与长期均衡关系；另一方面，构建时变参数状态空间模型，估算泉州市工业经济增长对新兴产业发展的弹性系数，以反映泉州地区新兴产业的发展态势，进而探索泉州市工业经济增长与新兴产业之间的动态互动关系。

一、理论基础

(一)协整关系

由多个非平稳的经济变量组合而成的经济系统，在短期内，受季节变动因素和其他随机因素的干扰，而使经济变量呈现出内部不均衡的非稳定状态；但从长期来看，这些经济变量会同步波动以致达到内部均衡。在统计学上，把这种短期偏离、长期均衡的关系称为协整。Engle和Granger提出了协整检验方法，通过协整检验可以判断一组非平稳序列的线性组合能否满足协整关系。

(二)误差修正模型

1978年，Davidson、Hendry、Srba和Yeo共同提出了误差修正(ECM)模型的基本形式，因此也可以把误差修正模型称为DHSY模型。ECM模型可以用来描述满足协整关系的经济变量之间的关系。ECM模型的估计方法最常用的是E-G两步法，适用于只有两个经济变量的情况。

(三)时变参数状态空间模型

状态空间模型被用来估计不可观测的时间变量，许多时间序列模型都可写成状态空间模型形式。动态系统和静态系统的最大区别在于它可以把不可观测的状态变量也就是时变参数并入可观测的模型，而且能够通过利用强有力的迭代算法(卡尔曼滤波)得到时变参数的估计值。值得一提的是，在状态空间模型中引入时变参数，有利于动态地了解经济变量之间的关系[2]171-182。

二、变量选择与数据来源

在解释变量和被解释变量选择时，要考虑到数据的可获得性，笔者采用泉州市统计信息网及福建省统计局网站的相关数据。选取了2007年～2016年的泉州市规模以上工业产值(y)作为被解释变量，泉州市五大新兴产业产值(x)作为解释变量，有效样本量为40个。考虑到数据分析的现实意义，同时削弱可能的异方差性，笔者对这两个变量的数据作自然对数处理。需要指出的是，结合研究的需要，笔者用泉州市规模以上工业产值对数(lny)差分与五大新兴产业产值对数(lnx)差分分别代表泉州市的工业经济增长与泉州市新兴产业发展。

三、实证分析

(一)泉州市工业经济增长与新兴产业发展的协整分析

1.平稳性检验

运用Eviews7.0对泉州市规模以上工业产值对数与五大新兴产业产值对数的时序数据进行ADF检验，其结果如表1所示。

表1 变量序列ADF检验

表1是在1%的显著性水平下得出的结论，可见应该拒绝变量Δlny和Δlnx存在单位根的原假设，从而认为Δlny和Δlnx是平稳序列，也就是说，变量lny和lnx属于1阶单整序列，即 lny～I(1)，lnx～I(1)。

2.协整检验

建立回归方程

lny=β0+β1lnx+μt。

运用Eviews7.0进行OLS回归，得估计的回归方程

lny=2.955 4+0.784 5lnx，

(1)

(12.89)(17.14)

对残差序列进行ADF检验，p值为0.000 0，说明残差序列在1%的显著性水平上通过了单位根检验，有理由相信泉州市规模以上工业经济产值与泉州市五大新兴产业产值之间存在协整关系。同时，协整向量为(1，-2.9554，-0.7845)T，相应的两个估计参数的t统计量值分别为12.89和17.14，说明在样本期内，泉州市规模以上工业经济产值与泉州市五大新兴产业产值之间存在长期稳定的均衡关系。

3.ECM分析

沿用E-G两步思想，模型设定为，

Δlnyt=β1Δlnxt-λecmt-1+μt，

其中，ecm表示误差修正项

ecmt-1=lnyt-1-α0-α1lnxt-1。

从模型估计的角度看，采用直接估计法时，模型的形式则设定为

Δlnyt=λα0+β1Δlnxt-λlnyt-1+λα1lnxt-1+μt,此时三个重要的参数分别为：泉州市工业经济增长的长期弹性系数α1；泉州市工业经济增长的短期弹性系数β1；λ为调整系数，表示由于短期波动造成泉州市工业经济产值偏离其长期均衡状态时，那么其自动向均衡点靠近的调整速度为λ。

运用Eviews7.0，采用直接估计法进行OLS回归，得估计的回归方程

Δlnyt=1.796 1+0.721 3Δlnxt-

(3.38)(8.99)

0.599 2lnyt-1+0.465 0lnxt-1，

(2)

(-3.61)(3.31)

Δlnyt=0.721 3Δlnxt-0.599 2ecmt-1；

(3)

ecmt-1=lnyt-1-2.9975-0.776 0lnxt-1；

(4)

由于此方程的参数是由利用直接估计法获得的参数计算而来的，相应统计指标的值未知。利用E-G两步法对ECM模型进行OLS回归，得回归方程

Δlnyt=0.721 7Δlnxt-0.581 5ecmt-1,

(5)

(9.71)(-3.67)

根据回归方程(5)，可以得到三个结论：第一，短期而言，泉州市新兴产业产值每增长1%，就会带动泉州市工业经济产值增长0.7217%；第二，-0.581 5说明在短期波动造成泉州市工业经济产值偏离其长期均衡状态时，其向均衡点靠近的调整速度为-0.581 5，换言之，非均衡状态下向均衡状态逼近的调整力度是-0.581 5；第三，当ecmt-1>0时，可以认为第t-1期泉州市工业经济产值向上偏离长期均衡点时，会以0.581 5的调整速度减少第t期泉州市工业经济产值，从而达到第t期泉州市工业经济产值向长期均衡点靠近的目的；当ecmt-1<0时，可以认为第t-1期泉州市工业经济产值向下偏离长期均衡时，会以0.581 5的调整速度增加第t期泉州市工业经济产值，从而达到第t期泉州市工业经济产值向长期均衡点靠近的目的[3]。

4.因果检验

用格兰杰因果检验考察泉州市工业经济增长与新兴产业发展的内在关系。鉴于2012年泉州市对规模以上企业统计口径进行了调整，所以分两个阶段进行Granger因果检验：第一阶段为2007年第1季度～2011年第4季度，第二阶段为2012年第1季度～2016年第4季度。检验结果如表2所示。

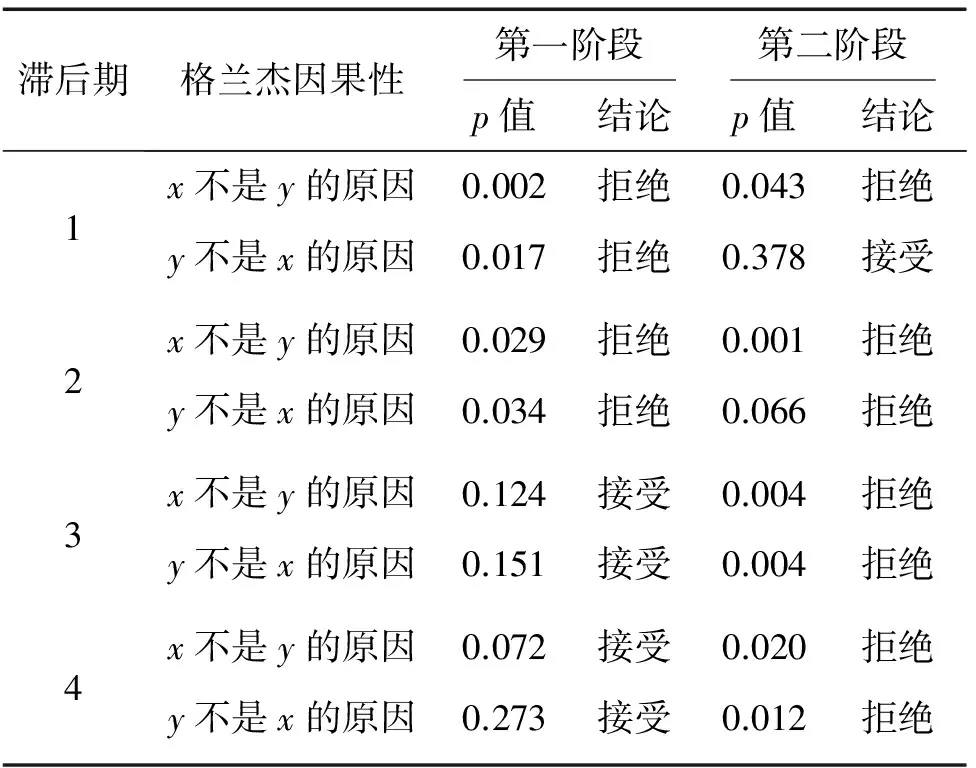
表2 格兰杰因果检验结果

从表2可见，在5%的显著性水平上，第一阶段滞后1～2期时，结论都是“拒绝原假设”，滞后3～4期时，结论都是“不拒绝原假设”。理论上，滞后1期的结论最有说服力，故可以认为新兴产业产值和工业经济产值互为格兰杰原因。因此，泉州市工业经济增长与泉州市新兴产业产值之间存在双向因果关系，这说明不仅新兴产业产值变动影响工业经济产值变动，工业经济产值变动也会影响新兴产业产值变动。第二阶段滞后1期的结论是新兴工业推动工业发展，而工业发展对新兴工业发展没有逆向推动作用；滞后2～4期的结论都是一样的，即新兴工业产值和工业产值互为格兰杰原因。

(二)泉州市工业经济增长与新兴产业发展的状态空间模型分析

利用状态空间模型对时变参数进行估计，试图了解泉州市工业经济增长对新兴产业发展的弹性系数随时间的变动情况，基本形式如下所述。

信号方程

lnyt=htlnxt+ct+νt，t=1，2，…，39，

(6)

状态方程

ht=dt+ftht-1+ωt，t=1，2，…，39。

(7)

运用Eviews7.0,利用卡尔曼滤波算法得到方程如下所述。

信号方程

(8)

状态方程

ht=0.0948+0.8705ht-1+ωt，t=1，2，…，39，

(9)

方程(8)估计的标准误差是0.368 2和0.507 1，方程(9)估计的标准误差是0.134 1和0.183 2。从方程(8)和方程(9)可见，信号方程和状态方程都在1%的显著性水平上通过了检验，ht为时变参数，即泉州市工业经济产值对新兴产业产值的弹性。ft=0.870 5≠0，可见时变参数ht具有自相关性，可以认为除泉州市新兴产业产值与工业经济产值的相互影响外，还存在其他未知的因素对二者的关系存在推波助澜的作用，而且该作用非常显著[4]。

泉州市2007年第1季度～2016年第4季度工业经济产值对新兴产业产值的弹性系数的变化趋势如图1所示。

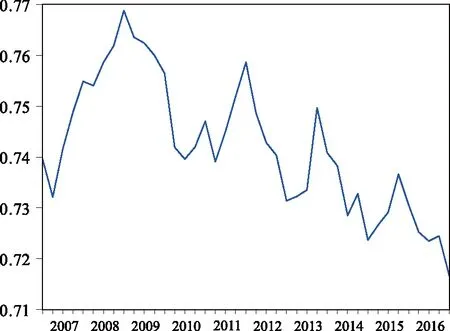
图1 工业经济产值对新兴产业产值的弹性

从图1中可以看出，在样本期间泉州市工业产值对新兴产业产值的弹性在0.717～0.769之间波动。表明在此区间，当泉州市新兴产业产值每增加1%时，工业经济产值增加幅度为71.7%～76.9%。可见，泉州市工业经济增长对于新兴产业发展的依赖程度是比较高的。最高峰值出现在2008年第4季度，从2008年第4季度开始，弹性系数震荡下降，2016年第4季度达到最低值。

那么为何弹性系数会呈现出图中的变动趋势呢？可以从这个时期的国际、国内经济环境着手对其进行分析。以下从美国次贷危机最终引发全球性的经济危机的视角对此弹性系数的变动趋势进行简要阐述。2007年第1季度～2008年第4季度期间弹性系数急剧上升说明泉州市工业经济发展对于五大新兴产业的依赖程度持续走高，此时期是经济危机对中国影响最为严重的两年，泉州市的产业经济对出口外贸的依赖性非常大，在世界经济局势非常恶劣的条件下，企业很难通过外贸途径实现产品的市场价值，扩大内需是这个时期大多数企业的市场战略导向。新兴产业由于其具有“规模小”“发展快”“市场窄”等特点，受金融危机的冲击比较小，在大多数产业处于低迷状态时，其依旧保持着稳定的发展趋势。2008年第4季度～2010年第1季度期间弹性系数急剧下降说明泉州市工业经济发展对于五大新兴产业的依赖程度持续走低，在经历两年经济危机的冲击之后，泉州市的传统支柱产业已经逐渐走出困境，同时在泉州市政府的政策支持下，传统的支柱产业普遍存在的“用工荒”问题也得到了适度的解决，新兴产业由于其依旧保持相对稳定的发展态势，使得工业经济整体发展对其的依赖性降低。2010年第1季度～2016年第4季度弹性系数反复波动说明泉州市工业经济发展已经重新步入正轨，在经历了前面两个经济发展阶段(萧条、复苏)之后，泉州市工业经济发展中的两个重要组成部分：传统产业和新兴产业的发展重新恢复到稳定状态。

四、结 语

(一)主要结论

通过上述关于泉州市工业经济增长与新兴产业发展之间关系的实证分析可以得出如下三个主要结论。

1.泉州市工业增长对新兴产业存在依赖关系

根据协整关系分析可知，2007年～2016年，长期均衡关系存在于泉州市工业经济增长和新兴产业发展之间，这种均衡关系具体表现为泉州市工业经济增长对新兴产业发展的依赖关系。同时，根据ECM分析可知，调整系数值为λ=-0.581 5，这表明：其一，负号表明当被解释变量(工业经济产值)偏离长期均衡点时所采取的是负反馈机制；其二，|-0.581 5|=0.581 5<1表明对被解释变量(工业经济产值)偏离长期均衡点的调整呈现出收敛状态。

2.泉州市工业经济对新兴产业存在逆向推动

根据Granger因果检验可知，2007年～2016年，不仅泉州市工业经济增长对新兴产业存在依赖关系，泉州市工业经济增长对新兴产业也存在逆向推动，这两种关系并存的现象反映了整体产业与局部产业之间的相互依存关系。同时，这种相互依存关系具有明显的时效性，从2007年第1季度～2011年第4季度的数据可知，随着时间的推移，依存关系呈现出减弱的趋势，大致依存的时间跨度为4个季度，即1年；可见在此期间内相对于新兴产业产值对工业经济产值的影响力而言，工业经济增长对新兴产业发展所带来的逆向推动作用稍显薄弱。而2012年第1季度～2016年第4季度期间工业经济增长对新兴产业发展所带来的逆向推动作用明显加强，其原因主要是新兴产业的发展也需要传统产业的支持，各产业的融合度不断加大。

3.泉州市新兴产业的市场稳定性明显优于传统产业

根据状态空间模型分析可知，在样本期内，泉州市新兴产业表现出了稳定的发展趋势，工业经济产值对新兴产业产值的弹性系数呈现出震荡的趋势。尤其是在全球金融危机背景下，2007年第1季度～2008年第4季度期间，金融危机对实体经济的冲击力度越大，泉州市工业经济产值对新兴产业产值的弹性系数就越大；2008年第4季度～2010年第1季度，金融危机对实体经济的冲击力度越小，泉州市工业经济产值对新兴产业产值的弹性系数就越小；2010年第1季度～2016第4季度，彻底摆脱金融危机困扰后，泉州市工业产值对新兴产业产值的弹性系数呈现出收敛震荡的态势。

(二)重要启示

针对上述三个主要推断性结论，以下结合当前泉州市经济发展的实际，笔者对泉州市未来产业经济的发展路径提出三个建议。

1.继续加强对新兴产业的政策扶持

鉴于新兴产业对于泉州市工业经济增长有极强的推动作用，所以加大对新兴产业的政策扶持力度成为促进泉州市产业经济持续、稳定发展的当务之急。当前，泉州市为了进一步推动新兴产业的发展，建立了以博士后科研工作站、软件产业园、生产力促进中心等为基础的一系列高技术企业孵化基地。新兴产业稳定发展的态势从另一个侧面说明其目前的市场化进程还比较有限，因此受到金融危机的影响也比较小。未来政策扶持可以考虑从新技术的市场应用推广方面着手，建立以市场需求为导向的泉州市新兴产业发展制度。

2.重点关注产业对时间的依存关系

当今社会是信息化社会，信息的传播在速度、数量、方式上均呈现出级数扩张的态势，可谓日新月异，尤其是对于具有一定规模的上市企业而言，瞬息万变的市场信息更是对产业的发展产生了极为重要的影响。对于产业的发展而言，信息化是一把双刃剑，利用好信息化平台的优势条件，可以让企业在较短的时间内占领市场、提高影响力；同时，一旦某个产业的发展出现危机可能会以更为迅速的方式影响其他的产业、市场或者企业发展。重点关注产业发展对时间因素的依存关系，无论从宏观层面还是从微观层面都是很有必要的。从宏观层面上看，可以考虑由泉州市政府牵头构建企业信息化服务平台或者构建独立的第三方决策咨询机构；从微观层面上看，企业之间可以通过建立行业协会或者聘请专业的市场分析师来保证企业发展过程中对富含时间效率的市场信息及时把握。

3.合理协调新老产业间的角色定位

传统产业的主要特点是规模大、发展慢、市场宽，与之相对应的新兴产业的主要特点是规模小、发展快、市场窄。两类产业所具有的不同特点决定了其在应对市场环境变化过程中所呈现出的不同状态：一方面，具有较大市场规模的传统产业对于现实市场环境变化较为敏感，其更大程度上属于实体经济范畴；另一方面，具有较小市场规模的新兴产业对于现实市场环境变化的敏感度较低，其更大程度上属于虚拟经济范畴。合理布局新兴产业与传统产业，对于工业整体升级乃至整个国民经济的发展都举足轻重。传统产业对泉州市经济发展的贡献率远大于新兴产业，应该继续扮演“支柱产业”的角色；新兴产业是泉州市未来经济发展的方向，已呈现良好的上升势头，在泉州市产业发展中扮演的是“生力军”的角色。

[1] 泉州统计年鉴2017[EB/OL].(2017-05-05).http://www.qztj.gov.cn/tjzl/tjsj/.

[2] 高铁梅.计量经济分析方法与建模——EViews应用及实例[M].2版.北京：清华大学出版社，2009.

[3] 李子奈，潘文卿.计量经济学[M].3版.北京：高等教育出版社，2010.

[4] 刘巍，陈昭.计量经济学软件：EViews操作简明教程[M].广州：暨南大学出版社，2009.

Study of Relationship Between Industrial Economy and New Industries of Quanzhou——Based on Space State Model of Time-varying Parameter

CHEN Qin, WANG Canxiong

(Jinshan College, Fujian Agriculture and Forestry University, Fuzhou 350002, China)

Through co-integrated Analysis and using the state space model of time-varying parameter, this paper makes an empirical research on the relationship between the industrial economic growth and development of the new emerging industry of Quanzhou according to the data from 2007 to 2016. The results show that, from the perspective of co-integrated analysis, there exists a long-term equilibrium relationship between industrial economic growth and the development of new industries in Quanzhou, and economic growth has 58.15% automatic repairing capacity. Grounded on the time-varying parameters, the coefficient of the dynamic elasticity of Quanzhou industrial growth affecting the output of the new industry fluctuates steadily, hovering from 0.717 to 0.769. At the same time, on the basis of empirical analysis, the paper puts forward enlightenments for the development of Quanzhou′s future industrial economy.

industrial economy; new industries; time-varying parameter; state space model

10.3969/j.issn.1674-5035.2017.06.005

F224.0

A

1674-5035(2017)06-0026-06

2017-06-26

陈 钦(1980-)，女，福建福州人，硕士，讲师，主要从事区域经济可持续发展研究. 王灿雄(1982-)，男，福建晋江人，硕士，副教授，主要从事区域经济可持续发展研究.

福建农林大学金山学院第一批应用型课程建设项目“应用统计学”资助项目(编号：K170208).

(责任编辑杨耕文)