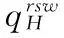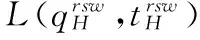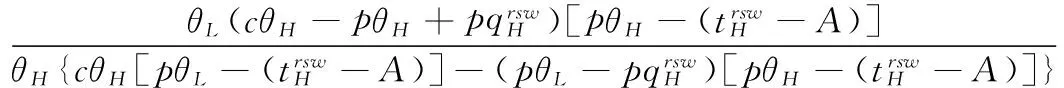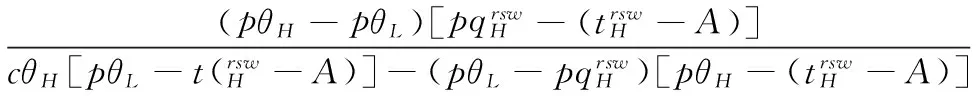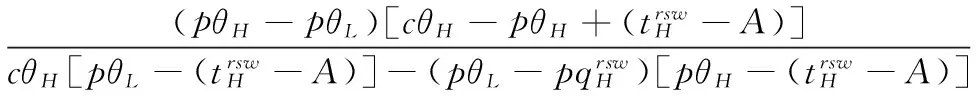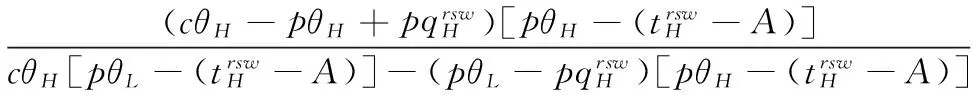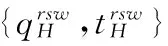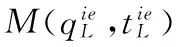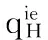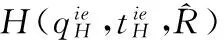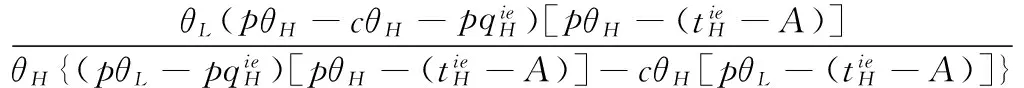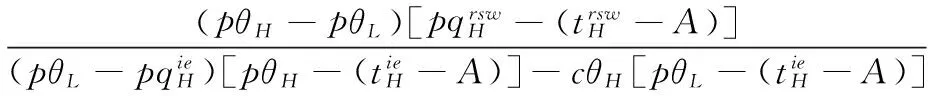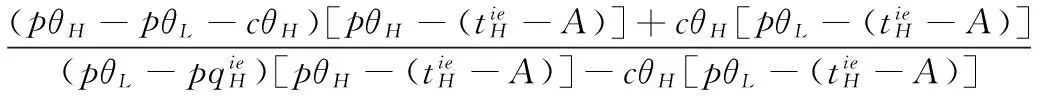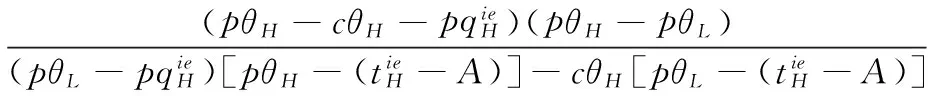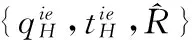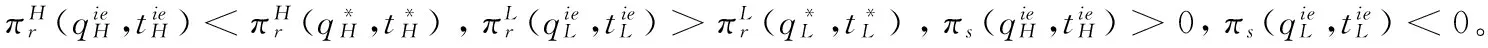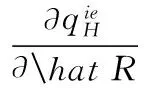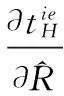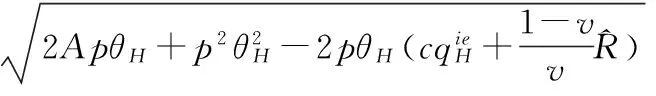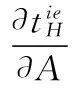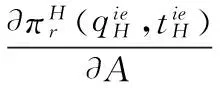零售商主导型供应链中的知情委托方赊销契约机制设计
2018-01-02鄢仁秀汪贤裕
鄢仁秀, 汪贤裕
(1.成都理工大学核技术与自动化工程学院 四川 成都 610059;2.四川大学商学院,四川 成都 610064)
零售商主导型供应链中的知情委托方赊销契约机制设计
鄢仁秀1,2, 汪贤裕2
(1.成都理工大学核技术与自动化工程学院 四川 成都 610059;2.四川大学商学院,四川 成都 610064)
为了研究供应链赊销交易中知情委托方向代理方进行信号显示的问题,考虑由一个供应商和一个零售商组成的二级供应链,双方进行赊销交易。零售商作为核心企业,拥有销售能力的私人信息。基于显示原理,首先设计了具有激励性质且保证供应商单独可获利的低信息密度最优配置,并分析了博弈的完美贝叶斯均衡。结果表明,知情零售商通过提供低信息密度最优配置向供应商传递信号,但存在信号成本,具体表现为:契约呈现“低端不扭曲,高端向上扭曲”特性;且对高能力零售商的初始资金有门槛要求。其次,通过分析知情零售商提供的事中有效配置发现,当供应商对零售商所属类型的信念满足一定条件时,低信息密度最优是事中有效的,此时博弈存在唯一的完美贝叶斯均衡。否则,由事中有效确定的均衡配置集弱帕累托占优于低信息密度最优;高能力零售商的信号传递成本相对降低,具体表现为:“高端向上扭曲”的程度相对较低,且向供应商提供初始资金的门槛要求也更低。本文的研究对供应链管理中,知情委托方的赊销契约设计问题提供了一定的理论基础和实践指导。
赊销;知情委托方;机制设计;低信息密度最优;事中有效;完美贝叶斯均衡
1 引言
随着零售业快速发展,沃尔玛、苏宁等众多连锁零售企业相继利用自身信用向上游供应商赊销。交易过程中,供应商可通过零售商订货量的增加获得产品市场占有率提升,但也往往会因为面临零售商销售能力的私人信息而遭受损失。例如,为有效利用有限货架或展位资源,部分零售企业(或连锁零售企业的部分门店)可能会违背与供应商的事前承诺,而根据季节性、畅销商品的实际情况陈列商品,从而损害供应商的利益导致交易失败。因此,为了保证交易达成,高能力零售商便有动机设计选择性契约,作为向供应商传递自身能力类型的信号。本文主要研究零售商主导型供应链赊销交易中的知情委托方契约机制设计问题。
近年来,众多学者在Goyal[1]研究的基础上从不同角度探讨了赊销交易中的库存优化问题。如Chen[2]在市场需求依赖于商业信用的假设下研究了零售商的最优订货策略。秦娟娟[3]在时变供需环境下探讨了基于商业信用的最优库存优化问题。还有不少学者探讨了供应商主导型供应链的契约协调问题。Lee和Rhee[4-5]、Chen Xiangfeng和WangAnyu[6]及张义刚等[7]分别讨论了收入共享、数量柔性、批发价格契约对供应链运作绩效的影响。近年来,零售商主导型供应链赊销交易中的协调问题也逐渐受到了学者的关注。刚号[8]研究得出供销双方的分散决策无法协调供应链,且存在最优的融资合约能实现供应链的协调。Mahata和Mahata[9]则利用模糊方法研究了零售商的订货决策。以上研究都是基于交易双方信息对称的假设,而对于信息不对称问题则较少涉及。针对零售商主导型供应链中信息不对称的研究,多集中于讨论资金充足供应链中的信息甄别问题。如Chen Fangruo[10],Özer和Raz[11], Çakany1ld1r1m等[12]探讨了以供应商生产成本为私人信息的批发价格契约。Wang等[13-14]在相同信息结构下分析了零售商如何通过二部定价契约、选择性契约真实揭示供应商的私人信息。徐晓燕和吴三平[15]研究了制造商谎报生产成本信息的行为对供应链绩效的影响。曹二保和赖明真[16]构建了基于委托销售的收益共享合约,分析了供应商的成本信息对链内各成员利润及渠道总利润的影响。颜波等[17]则探讨了双渠道供应链中,制造商的成本信息不对称时供应链的最优定价及对供应链的影响。以上研究均针对零售商通过设计契约对供应商进行信息甄别的问题。对于供应链实际运作中的知情委托方契约设计问题,现有研究中很少涉及。Maskin等[18-19]分别针对委托方私人信息具有私人价值与公共价值情形进行了理论研究,得出了相关的均衡契约配置。在此理论基础上,鄢仁秀和汪贤裕[20]分析了资金充足供应链中,拥有销售能力私人信息的零售商向供应商的信号显示问题。
本文将研究供应链赊销交易中,拥有销售能力私人信息的零售商作为核心企业,向供应商显示信号的问题。首先,在满足激励相容、单独可获利的条件下建立信号传递模型,并通过求解最小成本分离均衡,得到博弈的低信息密度最优赊销契约配置;然后求解博弈的事中有效配置,并得出博弈存在唯一完美贝叶斯均衡的条件。
2 问题描述与假设
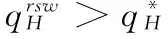
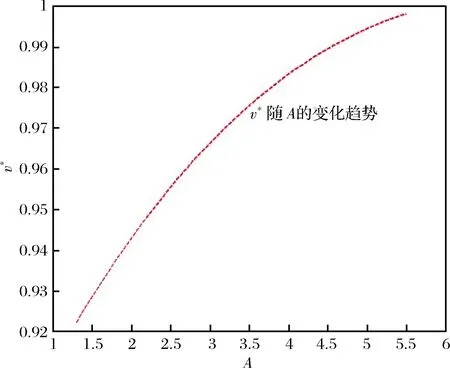
考虑由一个零售商与一个供应商组成的供应链,零售商作为核心企业,要求供应商提供赊销以缓解资金困境或获得快速扩张所需的周转资金。零售商的销售能力为θi∈{θH,θL}为其私人信息,θH>θL。供应商仅知道其类型为θH与θL的概率为v与1-v。零售商在交易前提供赊销契约{qi,ti},订货量qi由零售商根据市场需求x决定。假设x服从[0,θi]的均匀分布[21]。契约签订后,供应商获得零售商的初始资金A(A (1) πs(qi,ti)=E{min[pmin(x,qi),(ti-A)] (2) 本文直接借用鄢仁秀和汪贤裕[20]关于对称信息下最优赊销契约的结论作为此研究的基准。零售商的最优订货量、供应商理应获得的转移支付、两类零售商及供应商的期望利润分别为: (3) (4) (5) (6) 在求解过程中我们发现,对称信息下,两种类型零售商提供的初始资金均不存在门槛要求。即无论低能力或高能力零售商,均可要求供应商提供全额赊销。 零售商拥有销售能力私人信息时,为避免不同类型之间的模仿,须通过提供选择性赊销契约向供应商传递自身类型的信号,以保证双方赊销交易的顺利达成。因此零售商私人信息的存在将契约设计转化成了信号博弈问题。契约时序如图1所示: 图1 非对称信息下的博弈时序 为解决信号博弈可能存在多重贝叶斯均衡的问题,本文借鉴Maskin的方法[19-20],假定知情零售商向供应商提供选择性赊销契约({qH,tH},{qL,tL}),因为相对于“单选契约”(即每类零售商只提议一个契约选项),“选择性契约”既不会扩展配置集,且有助于剔除差的预期。 (7) (8) (9) (10) (11) s.t. (8)(9)(10)(11) 引理1 零售商至少可以获得低信息密度最优利润。 Tirole[22]曾证明了“弱单调利润”假定成立的条件下,分离配置是低信息密度最优的。本文将借用Tirole的方法求解规划P2H和P2L,首先判断“弱单调利润”假定是否成立。 因此,低信息密度最优契约配置可以由对称信息情形规划P1L以及下列规划P3H求得: (12) (13) (14) 命题1知情零售商提供的低信息密度最优赊销契约具有如下性质(证明过程见附录A): (15) (16) (3)无论面临何种类型零售商,供应商均仅能获得保留收益0。 (4)低能力零售商获得与对称信息情形一致的帕累托最优期望利润;而为了向供应商传递自身销售能力较强的信号,高能力零售商须付出信号成本,致使自身期望利润向下扭曲。 (5)为了顺利达成赊销交易,高能力零售商所提供的初始资金存在以下门槛要求: (17) Tirole[22]通过命题6.1指出,当且仅当低信息密度最优是事中有效时,博弈才有唯一的完美贝叶斯均衡。接下来将分析知情零售商能否通过契约改进获得更高的期望利润,即针对博弈是否存在完美贝叶斯均衡进行讨论。 (18) (19) (20) (21) (22) 命题2知情零售商提供的事中有效契约配置有如下性质(证明过程见附录B): (23) (24) (25) (26) (27) (3)为了向供应商传递信号,高能力零售商须付出信号成本,致使自身期望利润较对称信息情形向下扭曲。而对于供应商而言,面临高能力零售商时可获得正的期望利润,面临低能力零售商时则获得负的期望利润,其蒙受的损失转化为了低能力零售商的额外租金。 (4)为了顺利达成赊销交易,高能力零售商所提供的初始资金存在以下门槛要求: (28) 为避免低能力零售商的模仿,高能力零售商不得不以高于对称信息的订货量作为传递自身类型的信号,导致信号成本的产生。因此相较于对称信息情形,低信息密度最优和事中有效的订货量均具有“低端不扭曲,高端向上扭曲”特征。这一结论在现实中也有体现。国美每年都会向上游生产商订购高达1000亿的商品,但其销售额却不到1000亿。虽以其在零售渠道的影响力,可要求上游生产商在销售季末回购未售出商品,但在其销售经营过程中不得不付出库存成本及商品损耗成本。这就相当于国美为了证明自身实力所不得不付出的代价。 结论2低信息密度最优配置、事中有效配置,以及高能力零售商期望利润有如下特征: 结论3存在先验概率的临界值v*,当且仅当v≤v*时低信息密度最优是事中有效的,且是博弈唯一的完美贝叶斯均衡。反之则不存在唯一的完美贝叶斯均衡。v*由下列式子确定: (29) 结论4 信息密度最优和事中有效对低能力零售商所提供的初始资金无门槛要求;而对于高能力零售商而言,低信息密度最优对其初始资金的门槛要求更高。 图2 A对的影响 图3 A对的影响 图4 A 对v* 的影响 由图4可知,v*随A的增大而增大,此时条件v≤v*越容易得到满足,结合命题2可得,随着零售商初始资金的增大,低信息密度最优赊销契约配置为事中有效配置的可能性越大,博弈越有可能存在唯一的完美贝叶斯均衡。 本文研究了供应链赊销交易中,拥有销售能力私人信息的零售商作为核心企业,如何通过赊销契约的设计向其上游供应商进行信号显示的问题。基于显示原理,本文设计了一种具有激励性质且保证供应商单独可获利的低信息密度最优配置,并结合事中有效配置分析了博弈的完美贝叶斯均衡。结果表明,低信息密度最优具有“低端不扭曲,高端向上扭曲”特性,由此导致了高能力零售商的信号传递成本;且供应商对高能力零售商所属类型信念满足一定条件时,低信息密度最优是唯一的完美贝叶斯均衡。否则均衡配置集由事中有效确定,且弱帕累托占优于低信息密度最优。此时高能力零售商的信号传递成本相对降低,具体表现在订货量向上扭曲的程度低于低信息密度最优,且对高能力零售商初始资金的门槛要求也更低。 本文通过对供应链赊销交易中知情委托方契约机制的设计,得到了博弈的均衡配置,为供应链中类似问题提供了一个解决思路和方法。之后还可研究知情委托方向代理方传递信号,同时对代理人进行信息甄别(或减弱代理方的道德风险问题)的问题。 附录A (命题1的证明): 对于规划P3H,令λ与μ分别为约束(13)(14)式的乘子,构造拉格朗日方程: (A.1) (1-μ)θL<λθH<θL (A.2) (A.3) (A.4) 表达式(A.2)要成立,必须满足以下条件: (A.5) (A.6) (A.7) (A.8) (A.9) (A.10) (A.11) 附录B(命题2的证明): 1)首先对于规划Ι,令m为(19)式的拉格朗日乘子,构造拉格朗日方程: (B.1) 2)其次对于规划ΙΙ,令α与β分别为(21)(22)式的乘子,构造拉格朗日方程: (B.2) (1-β)θL<αθH<θL (B.3) (B.4) (B.5) -β(1-v)+α=0 (B.6) (B.7) (B.8) 因而可得: (B.9) (B.10) (B.17) (B.18) (B.19) (B.20) 附录C(结论1的证明): 2)其次,对于高能力零售商而言,由(25)(26)式可得: (C.1) (C.2) 由(B.9)(B.10))两式可得下列关系: (C.3) 由(27)(B.9)两式可得关系式(1-v)(pθH-pθL) (C.4) (C.5) 附录D(结论2的证明): 1) 首先对于低信息密度最优配置,由(15)(16)式可得: (D.1) (D.2) (D.3) (D.4) 2)其次对于事中有效配置,由(25)(26)式可得: (D.5) (D.6) (D.7) [1] Goyal S K. Economic order quantity under conditions of permissible delay in payments [J]. Journal of the Operational Research Society, 1988, 39(3):322-323. [2] Chen S C, Teng J T. Retailer’s economic order quantity when the supplier offers conditionally permissible delay in payments link to order quantity [J]. International Journal of Production Economics, 2014, 155:284-291. [3] 秦娟娟. 时变供需下基于商业信用的零售商最优订货策略[J]. 中国管理科学, 2016, 24(3):89-98. [4] Lee C H, Rhee B D. Coordination contracts in the presence of positive inventory financing costs [J]. International Journal of Production Economics, 2010, 124(2): 331-339. [5] Lee C H, Rhee B D. Trade credit for supply chain coordination [J]. European Journal of Operational Research, 2011, 214(1): 136-146. [6] Chen Xiangfeng, Wang Anyu. Trade credit contract with limited liability in the supply chain with budget constraints [J]. Annals of Operations Research, 2012, 196(1): 153-165. [7] 张义刚, 唐小我. 延迟支付下短生命周期产品批发价契约研究[J]. 中国管理科学, 2011, 19(3): 63-69. [8] 刚号, 唐小我, 慕银平. 零售商主导下融资服务对采购合同的影响 [J]. 系统工程, 2013, 31(4): 32-36. [9] Mahata G C, Mahata P. Analysis of a fuzzy economic order quantity model for deteriorating items under retailer partial trade credit financing in a supply chain [J]. Mathematical and Computer Modelling, 2011, 53(9): 1621-1636. [10] Chen Fangruo. Auctioning supply contracts [J]. Management Science, 2007, 53(10): 1562-1576. [11] Özer ö, Raz G. Supply chain sourcing under asymmetric information [J]. Production and Operations Management, 2011, 20(1): 92-115. [12] Cakanyildirim M, Feng Qi, Gan Xianghua, et al. Contracting and coordination under asymmetric production cost information [J]. Production and Operations Management, 2012, 21(2): 345-360. [13] Wang J C, Lau H S, Lau A H L. When should a manufacturer share truthful manufacturing cost information with a dominant retailer [J]. European Journal of Operational Research, 2009, 197(1): 266-286. [14] Wang J C, Lau A H L, Lau H S. Practical and effective contracts for the dominant retailer of a newsvendor product with price-sensitive demand [J]. International Journal of Production Economics, 2012, 138(1): 46-54. [15] 徐晓燕,吴三平. 生产成本信息不对称的两级供应链协调研究 [J]. 系统工程学报,2009, 24(1): 18-24. [16] 曹二保,赖明勇. 信息不对称的委托销售合约 [J]. 系统管理学报, 2009, 18(2): 199-202. [17] 颜波, 刘艳萍, 李鸿媛. 成本信息不对称下零售商主导的混合渠道供应链决策分析[J]. 中国管理科学, 2015, 23(12):124-134. [18] Maskin E, Tirole J. The principal-agent relationship with an informed principal: The case of private values [J]. Econometrica,1990, 58(2): 379-409. [19] Maskin E, Tirole J. The principal-agent relationship with an informed principal, II: Common values [J]. Econometrica, 1992, 60(1): 1-42. [20] 鄢仁秀, 汪贤裕. 非对称信息下供应链赊销交易中的最优契约机制[J].软科学, 2014, 28(12): 16-49, 94. [21] Perakis G, Roels G. Regret in the newsvendor model with partial information [J]. Operations Research, 2008, 56(1): 188-203. [22] Tirole J. The theory of corporate finance [M]. Princeton: Princeton University Press, 2010. Trade Credit Contracts Design by an Informed Principal in Retailer-dominant Supply Chain YANRen-xiu1,2,WANGXian-yu2 (1. College of Applied Nuclear Technology and Automation Engineering, Chengdu University of Technology, Chengdu610059, China; 2. Business School, Sichuan University, Chengdu 610064, China) Mechanism design by an informed principal needs to take into account the informational leakage taking place when offering a contract to the agent. In this paper, the problem of contract design by an informed principal under trade credit in supply chain is investigated. More specifically, a supply chain consisting of a risk-neural supplier and a risk-neural retailer is considered. As the core enterprise, the retailer finances the inventory using trade credit from the supplier. By the Revelation Principle, we design the low-information-intensity optimum allocation (LII) with incentive compatibility is designed, to realize the informational leakage to the supplier, and avoid the imitation between different types of retailers. By means of the mechanism way of deriving the equilibrium applied by Tirole, it is found that under the weak monotonic profit assumption, the separating allocation is the LII. It’s also shown that to sign the true type to the supplier, the optimal contracts for the retailer with higher ability entails an upward distortion, which causes signaling cost. And the degree of distortion decreases with the increase of the retailer’s initial capital. Meanwhile, the contracts have restrictions of the initial capital. Furthermore, the interim-efficient allocation (IE) is presented to analyze the perfect Bayesian equilibrium (PBE) of the game. It can be shown that the LII is the unique PBE for certain supplier’s ax ante belief. Otherwise, the set of equilibrium payoffs for the two types of retailers weakly Pareto-dominate the LII. And the (IE) still present the same distorted characteristic as the LII, but has lower restrictions on the retailer’s initial capital. Our research will provide some theoretical basis and practical guidance for the mechanism design by an informed principal under trade credit in supply chain. trade credit; informed principal; mechanism design; low-information-intensity optimum; interim-efficient; perfect Bayesian equilibrium 1003-207(2017)11-0085-09 10.16381/j.cnki.issn1003-207x.2017.11.009 F252.3;F273.1 A 2015-01-21; 2016-12-22 国家自然科学基金资助项目(71502037,71501019);教育部人文社科青年基金项目(15YJC630149,14YJC630020,14YJC630187);四川省教育厅人文社科一般项目(16SB0075);成都理工大学机械工程专业教学创新团队项目(10912-JXTD201501) 汪贤裕(1947-),男(汉族),江苏苏州人,四川大学商学院教授,博士生导师,研究方向:激励理论、博弈论等,E-mail:372151486@qq.com.
3 非对称信息下的契约机制设计

3.1 低信息密度最优配置


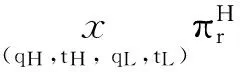
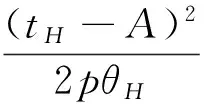
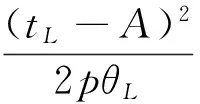
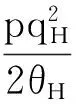
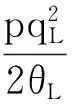
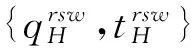
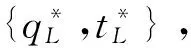
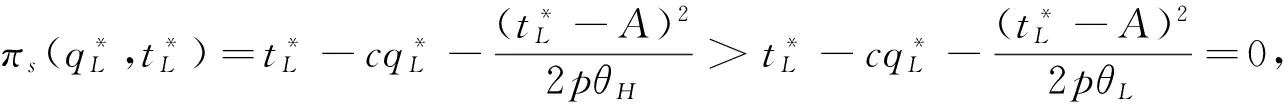
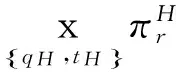
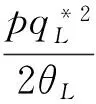
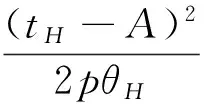
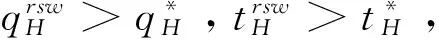
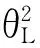
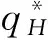
3.2 事中有效配置
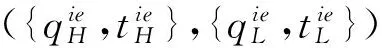
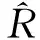
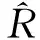
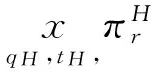
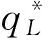
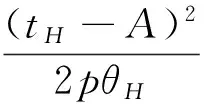

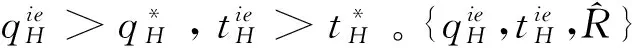
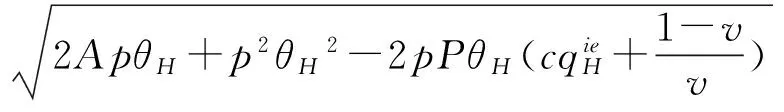
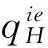
4 模型分析
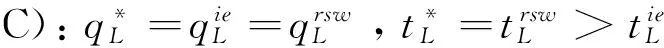
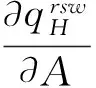
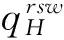
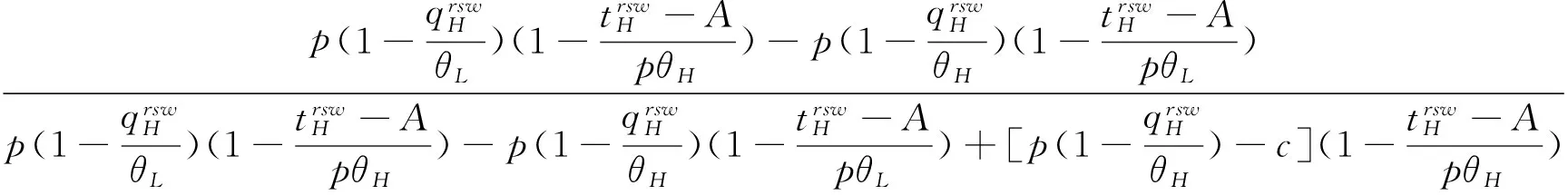
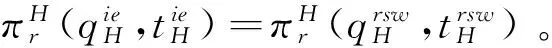
5 算例设计
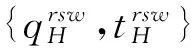
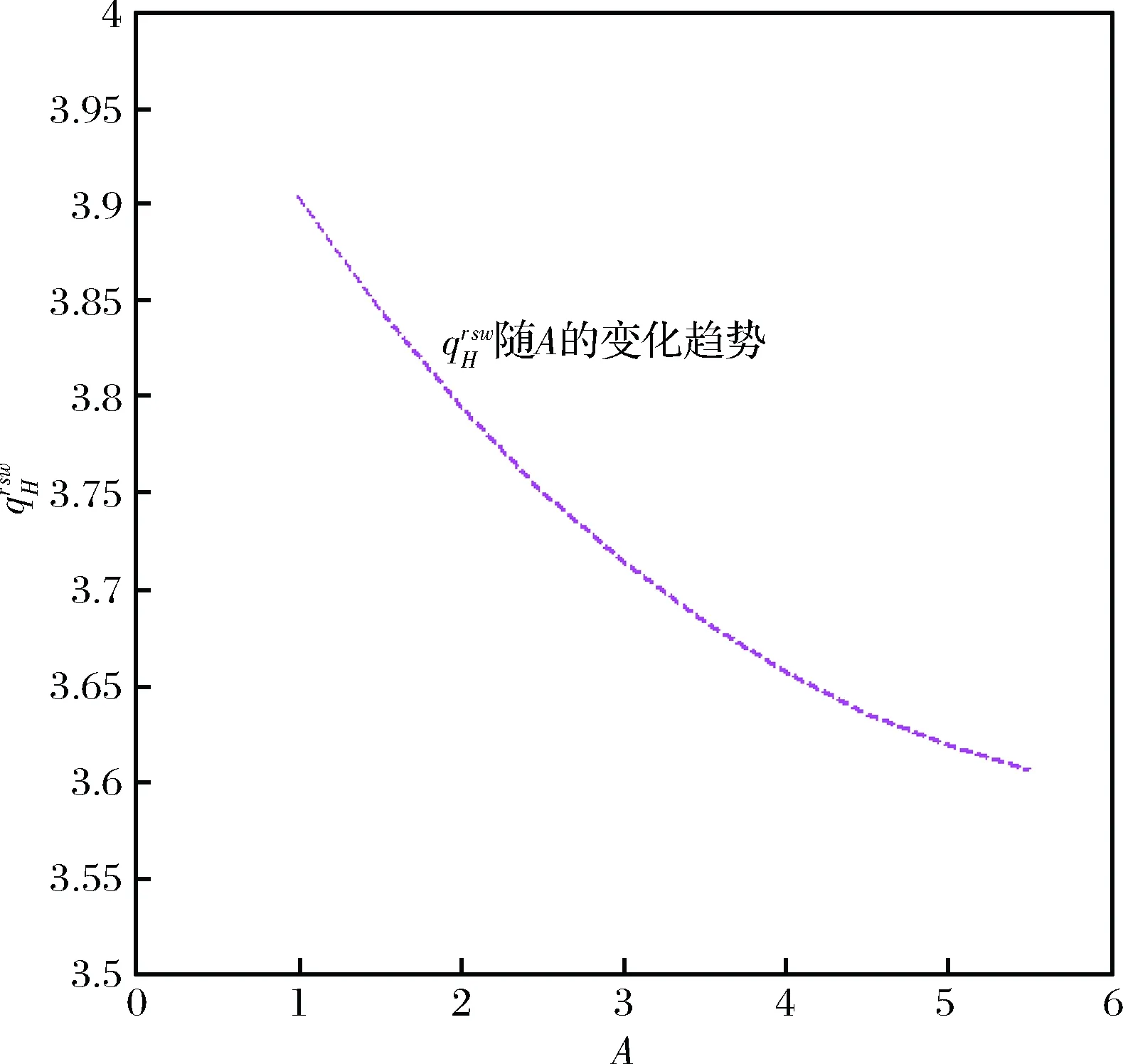
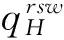
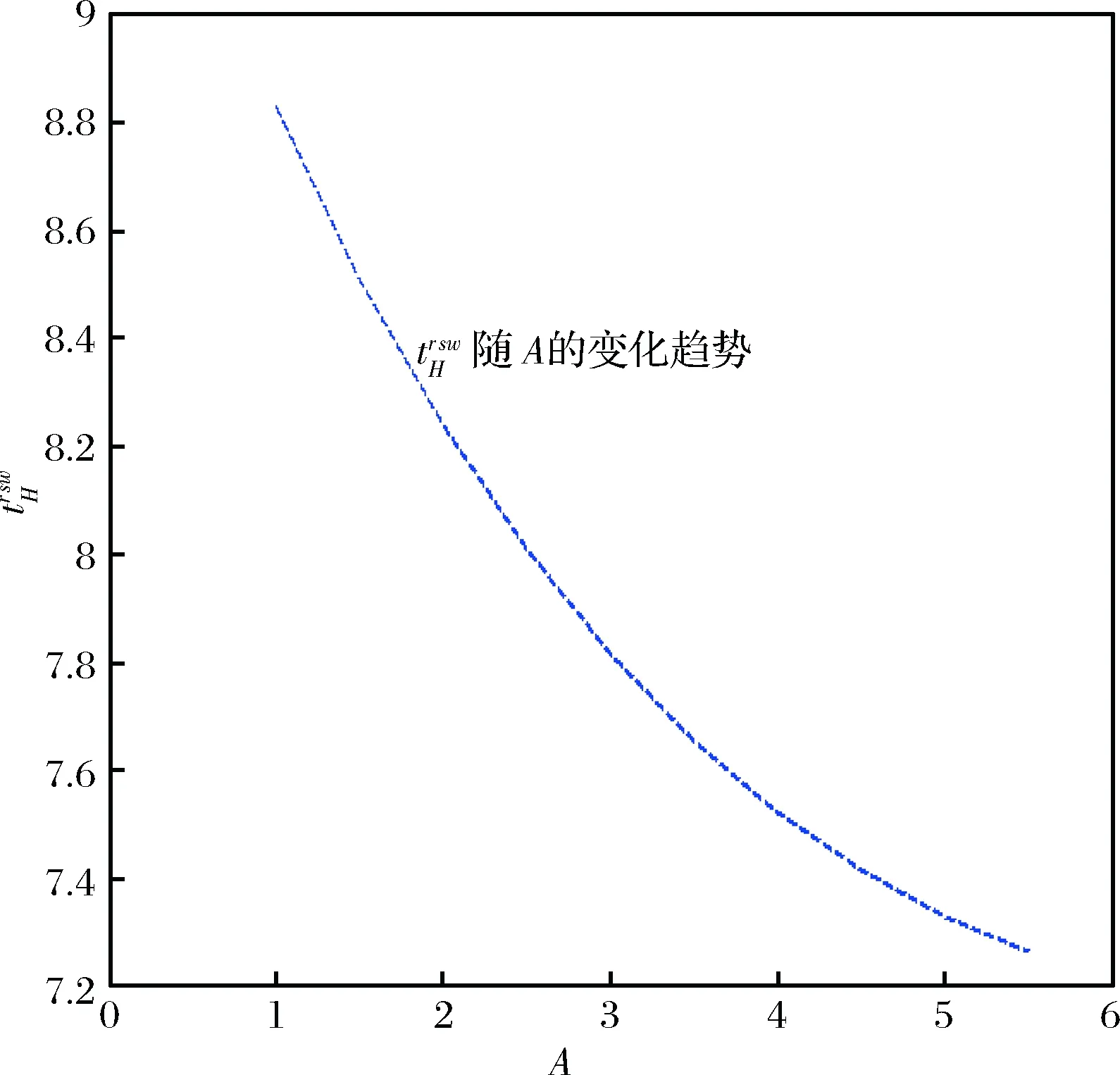
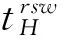
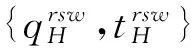
6 结语