基于变参数调整的电容电流测量方法探讨

师丽霞

（国网山西忻州供电公司，山西 忻州 034000）

基于变参数调整的电容电流测量方法探讨

师丽霞

（国网山西忻州供电公司，山西 忻州 034000）

在对配电网系统工作原理电路的模型进行改进的基础上，探讨了基于变参数调整的电容电流测量方法，即在保持变参数前后一定等量关系的前提下不断改变系统参数，然后构建关系式完成对地参数的测量，进而实现电容电流的测量，该方法具有一般性，可同时实现配电网对地电容以及对地绝缘电阻的测量。最后基于Matlab/Simulink平台搭建仿真模型，对电容电流测量方法进行验证，仿真结果验证了该方法的可行性和精确度。

模型改进；变参数调整；电容电流测量；Matlab/Simulink

0 引言

单相接地故障发生时，对于中性点经消弧线圈接地[1-2]的系统来说，故障点电流中的容性成分（即对地电容电流）通过调谐被消弧线圈产生的感性成分抵消，使接地点的电流大大减小，大幅度降低接地电弧发生的概率，提高配电网运行安全水平。为了更好地实现消弧线圈补偿，需要对系统电容电流[3-12]进行精确测量。所以，保证配电网系统安全运行，对地参数的精确测量显得尤为重要。

1 电容电流测量的基本原理

图1为中性点经消弧线圈接地系统图。

图1 中性点经消弧线圈接地系统图

图1为中性点经消弧线圈接地系统图。其中，Ubd为中性点自然不平衡电压；UA、UB、UC分别为电源A、B、C三相相电压；gL为消弧线圈并联电导；L为消弧线圈电感；gA、gB、gC分别为电源A、B、C三相对地电导；CA、CB、CC分别为电源A、B、C三相对地电容；K为开关。

现将中性点电压U0构造成受控电压源，此受控电压源系数为UA，并且以系统相电压 为基础量；系统三相电源支路、消弧线圈支路以及受控电压源与大地支路构成改进后模型的全部回路。系统工作原理电路改进模型如图2所示。

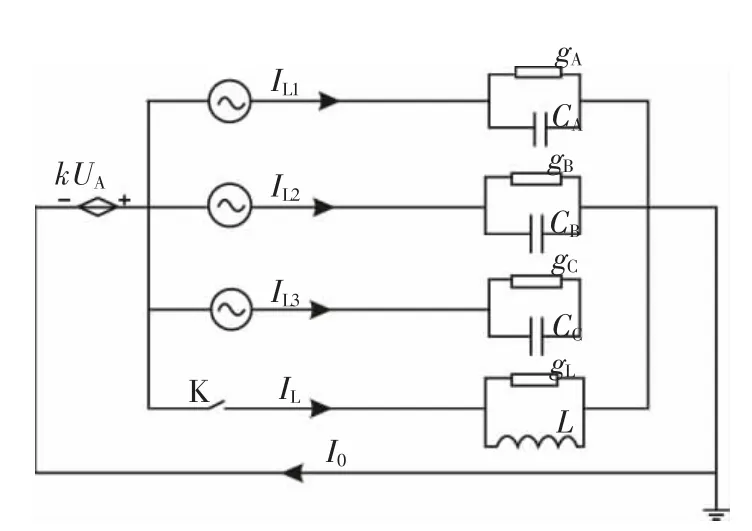
图2 中性点经消弧线圈接地系统工作电路改进模型

系统正常运行时的中性点电压表示为

其中，Yω=ωCΣ-1/（ωL） 为系统失谐量，CΣ=CA+CB+CC为系统总的对地电容；KZ=jωCA+gA+α2（jωCB+gB）+α（jωCC+gC）为系统参数不对称矢量和，其中 α=ej120°；gΣ=gA+gB+gC为系统总的对地电导，R为消弧线圈并联电阻。

对式（1） 两边去绝对值

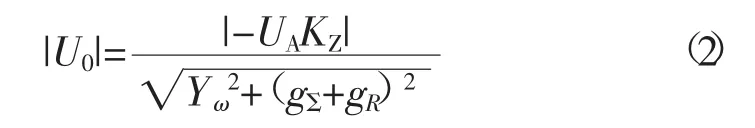
其中，｜U0｜为中性点电压幅值；参数量｜-UAKZ｜在三相对地电容及对地电导不变的情况下为一常数，因此消弧线圈电感量及与其并联的电阻将影响中性点电压幅值。

电容电流为

其中，Ubd＝U0（v－jd） 为中性点自然不平衡电压，其中U0中性点电压，为失谐度，d＝为阻尼率。

2 电容电流测量方法

根据分析可得到以下两种方案。

方案一：在消弧线圈并联电阻不变的情况下，调节消弧线圈电感量，使中性点电压幅值在不同补偿状态下不发生改变；方案二：在改变消弧线圈并联电阻的同时调节消弧线圈电感量，使中性点电压的幅值不发生改变，其中参数的设置可根据牛顿—拉夫逊法得到。

根据方案一可得变参数调整方法：设系统初始状态下失谐量 Yω＞0，即 ωC＞1/（ωL），消弧线圈处于欠补偿状态，记系统此时为状态1，消弧线圈电感量为L1，并联阻尼电阻为R1，测量得中性点电压有效值为U01；保持消弧线圈并联电阻不变即R2=R1，仅调整消弧线圈电感量为L2，使中性点电压幅值不变，即U01=U02，此时消弧线圈处于过补偿状态，系统脱谐量 Yω＞0，即 ωC＞1/（ωL），记录此时为状态2，消弧线圈电感量为L2。根据变化建立并联电阻不变时变参数调整关系，如图3所示。

在消弧线圈的不同补偿状态下，中性点电压幅值相同；在系统三相对地电容及对地电导不变情况下｜-UAKZ｜为一常数，结合图3中的变参数调整关系，可得式（4）。

图3 并联电阻不变时变参数调整关系图

结合变参数过程及调整前后消弧线圈的补偿状态的不同，由式（4） 可得式（5）。

解式（5） 可得系统对地电容表达式（6）。

方案一可实现系统对地电容的测量，但不能实现对地绝缘电阻的测量。根据方案二所述，分析该思路下可同时实现对地电容及对地绝缘电阻测量的方法，其具体变参数调整流程（参数的调整根据牛顿—拉夫逊法进行）。

设系统初始状态下消弧线圈电感量为L1，并联电阻为R1，测量得中性点电压幅值为U01，记系统此时为状态1；此后进行对消弧线圈电感量及并联电阻进行3次调整。一次调整为同时调整消弧线圈电感与并联电阻值为L2、R2，使中性点电压幅值保持不变，即U02=U01，记系统此时为状态2；二次调整为保持阻尼电阻不变R3=R2，仅改变消弧线圈电感量为L3，使中性点电压幅值改变为U03，即U03≠U02，记系统此时为状态3；三次调整为改变电感与电阻值分别为L4、R4，使中性点电压幅值保持不变，即U04=U03，记系统此时为状态4。根据上述变化建立3次变参数调整关系图，如图4所示。

根据图4所示3次变参数调整关系，可建立式（7） 方程组关系。

解式（7） 可求得系统对地电容及对地电导的表达式分别为式（8）、式（9）。

图4 3次变参数调整关系图

根据式（8）、式（9） 及式（3） 即可计算出电容电流的大小，且供电支路的增加（或减少）不会影响该方法对对地参数的测量。基于变参数调整的电容电流测量控制流程图如图5所示。

图5 基于变参数调整的电容电流测量控制流程图

3 基于变参数调整的电容电流测试方法

在中性点经消弧线圈并电阻接地的10 kV配电网系统中，设有5条分别为长度为L1、L2、L3、L4、L5的出线，其中包含长度为10 km、15 km、13 km的架空线，分别对应 L1、L3、L4；长度为6.3 km、5 km电缆线，分别对应L2、L5，并为PI型分布参数。1支路的A相有一个单相PI型线路等效模块L1A，长度为6 km，此线路参数等同于线路零序分布参数。系统中正序参数分布架空线的电感、电容和电阻分别为：1.21×10-3H/km、9.7×10-9F/km、0.17 Ω/km；电缆线的电感、电容和电阻分别为 0.26×10-3H/km、5.94×10-9F/km、0.06 Ω/km。零序参数分布架空线的电感、电容和电阻分别为：4.23×10-3H/km、6.6×10-9F/km、0.21 Ω/km。电缆线的电感、电容和电阻分别为：1.1×10-3H/km、376×10-9F/km、0.09 Ω/km。系统中 B1、B2、B3、B4、B5、B6、B7、B8 为单相断路器 (其中B1、B3、B5、B7分别控制电阻R1、R2、R3、R4，B2、B4、B6、B8 分别控制电感 L1、L2、L3、L4)。

基于变参数调整的电容电流测量方法具体仿真过程如下。

初始状态：设置断路器B1、B2为闭合状态，将消弧线圈的电感以及并联电阻接入系统，测量并记录此时中性点电压有效值为U01。

一次调整：设置断路器B3、B4初始为断开状态，并设置在0.5 s时刻闭合，改变接入系统的消弧线圈电感量以及并联电阻数值，保证中性点电压有效值在变参数前后不发生改变，测量并记录此时中性点电压有效值为U02，则有U01=U02。

二次调整：设置断路器B5、B6初始为断开状态，并设置在1 s时刻闭合，改变接入系统的消弧线圈电感量，但保持并联电阻参数不变R2=R3，仅改变消弧线圈电感量，测量并记录此时中性点电压有值为U03，则有U03≠U02。

三次调整：设置断路器B7、B8初始为断开状态，并设置在1.5 s时刻闭合，改变接入系统的消弧线圈电感量以及并联电阻数值，保证中性点电压有效值在变参数前后不发生改变，测量并记录此时中性点电压有值为U04，则有U03=U04。

经仿真实验可以看出：系统开始运行后，在0.5 s经历第一次调整，消弧线圈的电感量以及并联电阻均发生变化，短暂波动之后，系统中性点电压幅值与参数改变之前的中性点幅值相同；在1 s进行第二次参数调整，仅改变消弧线圈的电感量，短暂波动之后，系统中性点电压幅值稳定下来不等于参数改变之前的中性点幅值；在1.5 s经历第3次调整，消弧线圈的电感量以及并联电阻均发生变化，在经过短暂的波动之后，系统中性点电压幅值稳定下来并与参数改变之前的中性点幅值相同。根据数据以及式（6）、式（7）、式（8）计算所得地参数测量结果如表1所示。

表1 基于变参数调整的电容电流测量方法的仿真数据

从表1数据可以看出，基于变参数调整的电容电流测量方法的探讨中对地电容以及对地绝缘电导的测量误差均较小，测量结果精度高，为电容电流的测量以及中性点电压控制提供了保证。

4 结论

供配电系统中消弧线圈的投入可以提高其安全性和可靠性，但面对不同情况的供配电系统，若要实现系统安全有效地运行，需要在系统正常运行时精确测量系统对地参数。基于变参数调整的电容电流测量方法，在保持变参数前后一定等量关系的前提下不断改变系统参数，然后构建关系式完成对地参数的测量,该方法具有一般性，可同时实现配电网对地电容以及对地绝缘电阻的测量，进而实现配电网电容电流的测量。

[1] 要焕年，曹梅月.电力系统谐振接地 [M].2版.北京：中国电力出版社，2009：81-82.

[2] 李继红.中性点经消弧线圈接地方式及并联中值电阻选线方法介绍 [J].内蒙古电力技术,2007，25(5)：33-36.

[3] 张战永，王建领，康怡，等.调容式消弧线圈自动补偿系统的实现 [J].电力系统保护与控制,2005，33(16)：90-92.

[4] JIN Wei,YUAN Pengsheng,ZHANG Yang,et al.A method of measuring capacitive current in distribution network based on adjusting the neutral grounding impedance[J].Power Systems Protection and Control，2015， 43(7)：37-41.

[5] 曾祥君,易文韬,刘张磊,等.注入信号精确谐振测量配电网电容电流新技术 [J].电力系统自动化，2008，32(4)：77-80.

[6] ZENG Xiangjun,YI Wentao,LIU Zhanglei,et al.A novel technique of capacitive current resonance measurement with signal injected for distribution networks[J].Automation of Electric Power Systems，2008，32(4)：77-80.

[7] 裴善鹏，连鸿波，李万彬，等.快速调匝式消弧线圈及接地选线一体化装置研究 [J].现代电力,2006，23(1)：20-24.

[8] 刘宝稳，李晓波.基于失谐量的消弧线圈跟踪调谐方法[J].电力系统保护与控制，2013(05)：6-9.

[9] 熊娅俐，陈乔夫，盛建科，等.基于注入信号的消弧线圈电容检测方法 [J].高电压技术.2005，30(03)：33-34.

[10] 庞清乐,孙同景,穆健，等.气隙调感式消弧线圈控制系统的设计 [J].高电压技术,2006，32(04)：34-37．

[11] 陈忠仁,吴维宁.调匝式消弧线圈自动调谐新方法.电力系统自动化,2005，29(24):75-78.

[12] ZHU Shuai,LI Xiaobo,CHENG Yukai,et al.Study on a new tuning method based on arc suppression coil[J].Electrical Measurement&lnstrumentation,2010，49 (8)：10-13.

The Method of Capacitance Current Measurement Based on Variable Parameter Adjustment

SHI Lixia
（State Grid Xinzhou Power Supply Company of SEPC,Xinzhou,Shanxi034000,China）

The working principle model of distribution network system is improved，and on that basis,the method of capacitance current measurement based on variable parameter adjustment is discussed.Tobe specific,the method is changingthe systemparameters in the premise that the variable parameters must keep equivalent relationship before and after,and then establish relation for grounding parameters measurement so that the measurement of capacitance current could be realized.The method can be generally used to measure the capacitance to ground and the insulation resistance.Finally,the simulation model is built based on Matlab/Simulink platform,and the method ofcapacitance current measurement is verified.The simulation results showthe proposed method is feasible and accurate.

model improvement;parameter adjustment;capacitance current measuring;Matlab/Simulink

TM835.2

A

1671-0320（2017）06-0018-04

2017-07-19，

2017-10-20

师丽霞（1989），女，山西代县人，2016年毕业于中国矿业大学电气工程专业，高级工程师，主要研究方向为供配电安全技术。