角分辨光电子能谱数据的快速拼接算法设计
2017-12-29贾小文
贾小文
(陆军军事交通学院 基础部,天津 300161)
1887年,赫兹发现当入射光照射到金属表面时,会有电子从金属表面逸出. 1905年,爱因斯坦提出了“光电子”的概念,从量子力学的角度完美地解释了光电效应. 由于光电子携带了材料内部电子结构的信息,因此可以通过探测光电子来研究材料的电子结构,角分辨光电子能谱就是该原理的具体应用[1-3]. 实验上,通过电子能量分析器探测出射的光电子,得到数据为某一方向立体角内电子的统计数. 从实验得到的光电子统计数是按照角度分布的. 为了方便研究,需要将角度转换为动量(实际上是动量在kx-ky面上的投影),经过转换后的数据为光电子统计数随动量(kx,ky)的分布. 在角度空间分布于一条线上的光电子(目前主流探测器都是这种模式),转换到动量空间的分布是一条弯曲的曲线. 因此要获得某个动量平面内所有光电子的分布,就要求对各个不同角度下(通常这个角度就是测量样品的取向)的测量数据进行拼接[4]. 在拼接数据时,传统的方法先由角度换算为动量,然后在动量空间进行均匀插值,这种方法存在耗时较大的缺点. 由于角分辨光电子能谱实验要求极度清洁的样品表面,如果耗时过长,样品清洁度将会下降,从而导致实验失败. 因此无论是从数据处理效率还是从开展实验的角度来看,都需要对传统的方法进行改进.
本文充分考虑了角分辨光电子能谱实验数据的相邻倾角数据基本类似的特点,提出了快速数据拼接算法,该算法首先生成均匀分布的动量点,然后逆用角度动量转换公式获取对应的角度值,最后在角度空间进行插值. 由于避开了普通插值的三角剖分和几何排序等复杂过程,可将运算速度提高2个数量级.
1 角分辨光电子能谱实验原理及数据的拼接
角分辨光电子能谱实验的基本原理是光电效应,如图1所示. 探测器收集电子的窗口是1条狭缝,1次收集1个狭长立体角空间的所有电子. 原始数据为网格化的矩阵,横坐标是动能,纵坐标是角度,数据表示光电子的谱重,如图2所示. 处理数据时,需要将角度转换成动量,转换的公式取决于样品与电子探测器相对方位的布局和定义. 以文献[4]为例,分析器相对于样品的角度定义取图3所示定义:将与狭缝平行的方向定义为偏转角度φ,与狭缝垂直的方向定义为倾角θ,样品转过的角度定义为旋转角ω[4-5]. 动量(kx和ky面的投影)和实验测量角度的转换公式为
(1)
式(1)中,k0表示出射电子的动量,由式(2)决定:

(2)
从式(1)中可以看到,探测器探测到的动量实际上是水平方向的动量,因此角分辨光电子能谱经常用于研究电子结构二维性较好的材料.
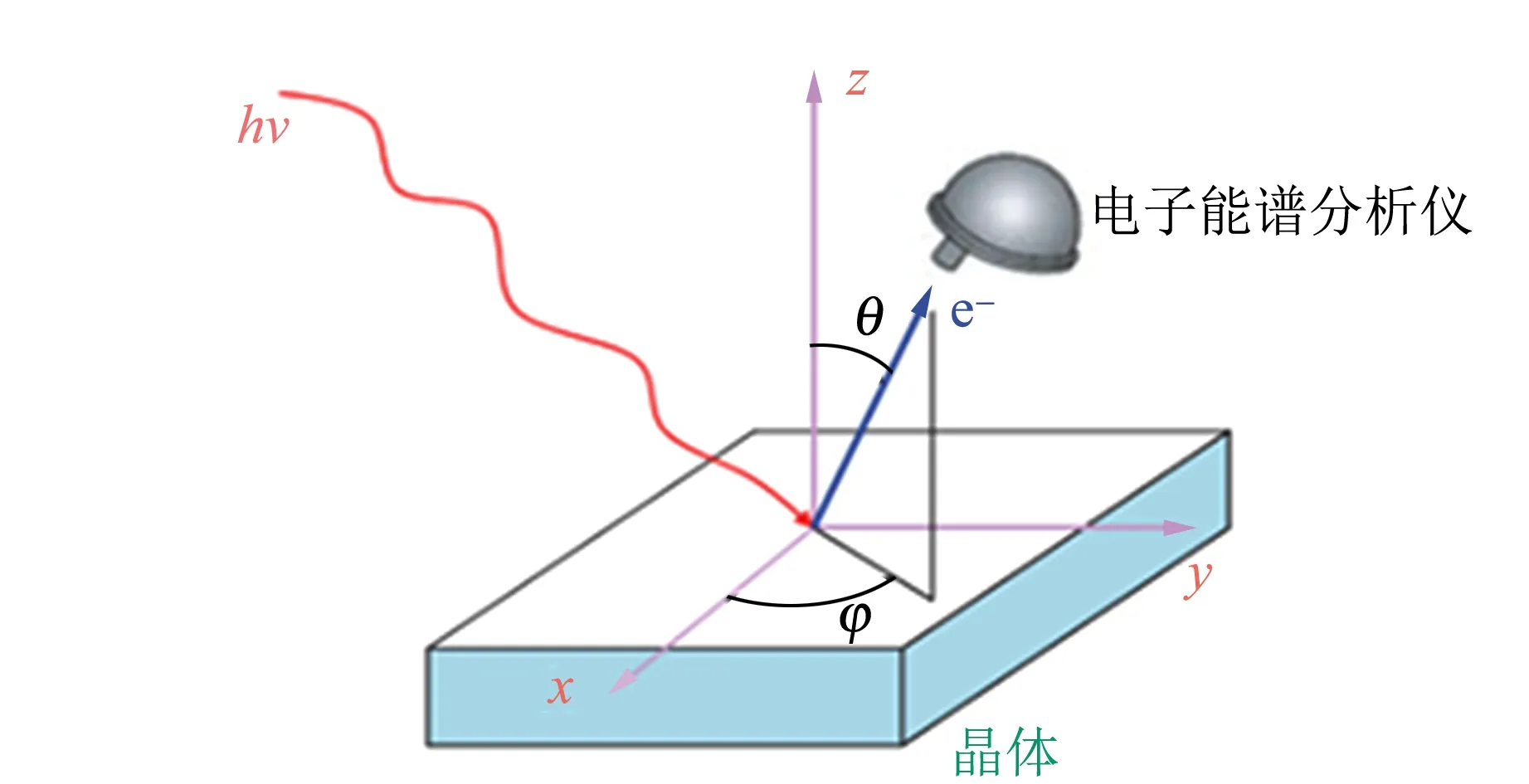
图1 角分辨光电子能谱实验基本原理示意图

图2 典型角分辨光电子能谱原始数据图谱

(a)绕样品面法向旋转角度为0时,偏转角度φ、 倾角θ与动量的换算关系

(b)绕样品面法向旋转ω角度后动量的换算关系图3 实验中样品、探测器狭缝取向与动量换算几何关系
为了得到不同动量区域的光电子信息,需要不断地改变狭缝相对于样品的倾角θ,并将这些数据拼接在一起. 在拼接时,图2中的原始数据在角度空间是均匀分布的,但是利用式(1)转换到动量空间(其实是kz=C的某个平面)后,(kx,ky)就不再是均匀的网格分布了,有些动量点有数据,有些动量点则没有数据,如图4所示.
图4(a)所示为铁基超导体FeSe0.3Te0.7在20 K下费米能级处谱重随动量的分布(光子能量22.218 eV,光电子能谱仪为Scienta公司的R4000),可以看到图4(a)的数据分布并不均匀,有些点有数据,有些点没有数据(相当于谱重等于0),是非均匀分布的数据图. 出现这种情况的原因有:1)角度到动量的转换算法[式(1)]是非线性的,连续均匀的角度分布换算到动量空间就不再是连续均匀分布了;2)探测器在倾角方向分辨率太大(倾角人为设定,一般是1°~2°,远大于探测器狭缝方向的角度分辨率),数据呈现明显的条状分布. 这种非均匀分布的数据给后续的分析带来不便,实践中需要将图4(a)的结果通过插值拼接成分布连续、光滑的数据,如图4(b)所示. 拼接的过程中需要解决数据不均匀分布的问题,即非均匀数据网格化.

(a) 直接将角度转换成动量

(b)插值拼接以后的结果 图4 费米能级处谱重随动量的分布
2 非均匀数据网格化
非均匀数据网格化是常见的数据处理方法,有非常成熟的数值算法,其过程是先对自变量空间进行三角剖分,再利用三角剖分结果重新抽样. 很多软件(如Igor,Matlab等)都有相应的函数完成上述运算. 这里介绍Igor下的做法[6-7].
首先创建N×3维的矩阵M,对每个倾角下的谱应用式(1)计算(kx,ky),分别记录在M的第1列和第2列,M的第3列存放对应的测量值. 然后利用ImageInterpolate命令进行插值运算:
Imageinterpolate/S={x0,dx,x1,y0,dy,y1}
Voronoi,M
以上做法是目前角分辨光电子能谱实验中数据拼接的传统做法,图4(b)的结果就是利用该方法计算得到的,其缺点是运算时间过长,通常需要1 min左右(取决于谱的数量),甚至更长. 耗时来源于三角剖分过程及以三角剖分为条件的插值几何排序过程.
3 快速数据拼接算法
三角剖分法适用的范围广,但某些应用场合效率较低. 实际上,角分辨光电子能谱实验数据有自己的特点:数据的自变量并非完全随机分布,相邻狭缝之间除了倾角不同,其他的实验条件完全相同. 根据这个特点构建了快速拼接算法:逆用式(1)从动量值反过来推算角度,利用角度值在原始数据中插值,将插值作为该动量处的结果. 快速拼接算法的优点是:
1)在动量空间,可以预先定义均匀分布的网格数据,省去了重新抽样的过程;
2)在角度空间,由于数据的分布是完全均匀的,可直接通过线性插值来获取插值结果,省去了三角剖分的计算过程.
快速拼接算法的复杂度为O(n),因此运算速度非常快. 实验结果表明:快速拼接算法要比传统算法运算速度提高2个数量级.
快速拼接算法的详细描述如下:
1)创建矩阵M(kx,ky).
2)取出(kx,ky),逆用式(1)计算(θ,φ).
3)对原始测量数据通过偏转角、倾角进行排序,找出相邻倾角θ1和θ2,使得θ1<θ<θ2,φmin<φ<φmax.φmin和φmax为原始谱最小角和最大角加上偏转角φ.
4)设θ1对应的原始数据是data1,θ2对应的原始数据是data2,利用双线性插值分别获取2个值z1=data1(0)(φ),z2=data2(0)(φ). 这里0表示费米能级.
5)通过线性插值得到(θ,φ)处数据:

6)将M中(kx,ky)处相应的值设置为z.
下面是算法具体实现(Igor代码):
variable N
Make/O/N=(N,N) M_FS
〈setscale〉
〈get wtheta, wphi, womega, wdatas〉
Sort {wtheta, wphi} wtheta, wphi, womega, wdatas
M_FS=render_FS(x, y, wtheta, wphi, wdatas)
Function render_FS(kx, ky, wtheta, wphi, womega, wdatas)
variable kx, ky
wave wtheta, wphi, womega wave/wave wdatas
variable omega=womega[0]
variable kx1, ky1, theta, phi
variable k0=sqrt(2*me*e0)/hb*sqrtEk/1E10*LA/pi
kx1=kx*cos(omega)-ky*sin(omega)
ky1=kx*sin(omega)+ky*cos(omega)
phi=asin(kx1/k0)
theta=asin(ky1/k0/cos(phi))
theta=theta*180/pi
phi=phi*180/pi
〈get ipos using (theta, phi) from wtheta, wphi〉
wave w1=wdatas[ipos]
wave w2=wdatas[ipos+1]
z1=w1(0)(phi)
z2=w2(0)(phi)
return (z2-z1)/(theta2-theta1)*(theta-theta1)+z1
end
4 实验结果
以图4所示数据拼接为例,对上述算法进行测试. 测试数据一共有77张谱,每张谱在角度方向的数据长度为360.
图5是快速拼接算法给出的插值结果. 可以看到图5(a)和图4(b)的结果几乎没有区别. 为了进一步确认快速拼接算法的可靠程度,图5(b)给出了沿不同方向切面[ProfileLine,方向如图5(a)中红色虚线箭头所指]的动量分布曲线(Momentum distribution curves,MDC),为了方便比较,曲线都进行了归一化. 可以看出快速拼接算法在曲线数据特征如峰位、半高全宽等方面与传统算法是一致的. 尽管如此,如果仔细观察,传统算法和快速拼接算法还是存在一些微小的差异. 出现这种现象的原因主要是插值机制的区别. Igor下传统算法使用的泰森多边形插值(Voronoi interpolation)是平滑插值方法,而本文中的快速拼接算法则完全采用线性插值. 另外,由于计算过程不同,计算机的舍入误差也会给插值结果带来一些差别.

(a) 快速拼接算法对费米面附近谱重随动量分布的拼接结果
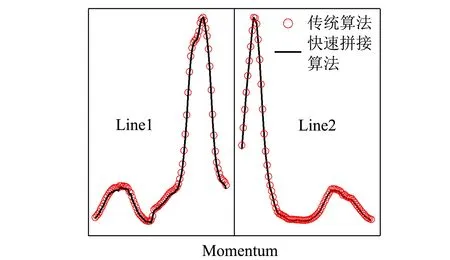
(b)动量分布曲线图5 快速拼接算法结果
表1给出了Igor Pro (Ver 6.37)下二者所用时间的对比. 从表1可以看出快速拼接算法的运算速度要比传统算法提高了近200倍.
利用多线程技术,还可以将快速拼接算法并行分配到多个处理器(多线程),能够进一步将运算速度提高到300多倍. 多线程实现的方法如下(Igor代码):
1)将渲染函数render_FS声明为线程安全函数.
Threadsafe function render_FS(…)〈function body〉End
2)利用multithread指令调用渲染函数对M_FS赋值.
Multithread M_FS=render_FS(x, y, wtheta, wphi, wdatas)
快速拼接算法(多线程)和传统三角剖分算法运行消耗时间比较如表1所示.

表1 快速拼接算法、多线程和传统三角剖分算法运行消耗时间比较
注:CPU I3-3320 4核处理器,3.3 GHz. RAM:2.00 G.
5 讨 论
原始数据谱的数量不同,每张谱的分辨率不同,无论是传统算法还是快速拼接算法,所用的时间都是不同的. 大量的实验结果表明,对于常见的角分辨光电子能谱实验,传统算法插值需要的时间集中在30 s~3 min,而快速拼接算法时间基本不会超过1 s,因此快速拼接算法对于速度的提升和本文中的例子(~200倍)基本一致,大概2个数量级. 在实践中,采用快速拼接算法,可以实时获取插值结果,这在使用传统算法时是不可能实现的.
快速拼接算法的适用范围要比传统算法的适用范围窄. 当测量不同动量空间是通过旋转样品(以样品面法向为旋转轴)进行时,快速拼接算法就不再适用了.
对于常见的角分辨光电子能谱实验,通常是通过改变样品相对于分析器的倾角来测量不同的动量空间,相邻倾角(通常少于2°)之间的数据差别不是很大. 快速拼接算法正是利用了这一特点对相邻倾角之间不存在的角度用两相邻数据线性插值结果来代替,这和传统插值算法从插值原理上来说并没有本质区别(此时平滑插值可以用线性插值近似),因此快速拼接算法和传统插值算法的插值结果一致. 但是由于跳过了三角剖分和插值几何排序等复杂耗时的计算过程,快速拼接算法提高了运算速度.
需要注意的是无论是快速拼接算法还是传统算法,都是通过已测数据推断未测量点的数据,从这点来说,本文所述传统方法亦不能作为绝对的参考,真正的插值效果有赖于待插值的数据环境. 事实上,还有其他的不同的插值方法,如最近邻法、克里金法(Kriging)等,这些方法同样能将非均匀分布的数据拼接为均匀分布的数据,但是插值的结果之间必然会存在一些差别.
利用快速拼接算法,可以实时查看不同结合能处谱重随动量的分布,还可以动态显示谱重动量分布随结合能的变化,这可以提高角分辨光电子能谱数据处理效率.
[1] 黄昆,韩汝琦. 固体物理学[M]. 北京:高等教育出版社,2010:213-223.
[2] Damascelli A, Shen Z X, Hussain Z. Angle-resolved photoemission of the cuprate superconductors [J]. Rev. Phys., 2002,75(2):473-541.
[3] Zhou X J, Cuk T, Devereaux T, et al. Angle-resolved photoemission spectroscopy on electronic structure and electron-phonon coupling in cuprate superconductors in handbook of high-temperature superconductivity [M]. New York: Springer, 2007:87-144.
[4] Liu G D, Wang G, Zhu Y, et al. Development of a vacuum ultraviolet laser-based angle-resolved photoemission system with a superhigh energy resolution better than 1 meV [J]. Rev. Sci. Instrum., 2008,79:023105.
[5] 贾小文. 角分辨光电子能谱对重费米子超导体CeCoIn5和铁基超导体Fe(SexTe1-x)的研究[D]. 北京:中国科学院物理研究所,2017.
[6] 丁永祥,夏巨谌. 任意多边形的Delaunay三角剖分[J]. 计算机学报,1994(4):270-275.
[7] Wavemetrics, Inc. The manual of IGOR Pro [Z]. 2015:1516-1518.
