工作要素在装配线中分配与其平衡率的研究
2017-12-28高振豪苏贵影李彦华余燕尾
高振豪, 苏贵影, 李彦华, 余燕尾
(1.中北大学经济与管理学院创新研究中心, 太原030051;2.天津工业大学管理学院, 天津300387)
工作要素在装配线中分配与其平衡率的研究
高振豪1, 苏贵影1, 李彦华1, 余燕尾2
(1.中北大学经济与管理学院创新研究中心, 太原030051;2.天津工业大学管理学院, 天津300387)
随着信息与时代的飞速发展,我国电子产品的大量需求订单导致企业装配线超负荷运行,装配线“瓶颈”现象凸显。为了解决装配平衡问题,部分企业采用之前的启发式工位分配方法,但是未能达到最优状态。借助最大化候选原则和Kilbridge&Wester法安排工作要素,使用Lingo11.0求解构建数学模型的平衡率、平滑指数以及节拍做对比,以此发现三者之间工作要素的不同安排影响整个装配线平衡率,且构建数学模型求解的平衡率较高。通过电子仪器装配线实例分析,证明数学模型的有效性,能够满足各项工艺要求,求解结果能有效解决其装配线平衡问题。
工作要素;平衡率;最大化候选原则;Kilbridge&Wester法
引言
生产运作的高效、合理是精益制造的最终目标,是快速灵动的对各种需求做出相应的快速反应,并产出高品质产品的生产管理技术。在精益生产思想的指导下如何不断地优化装配线,减少浪费、令其能够充分发挥能力,保持高效运作的状态,达到最佳平衡,这是当今企业的研究热点。刘俨后等人针对装配线随机作业时间的装配线平衡问题,以最小节拍为优化目标,构建随机作业下的第二类装配线平衡模型,并提出双染色体GA算法对该平衡问题进行求解[1]。张晓玲运用了传统工业工程中的程序分析和方法研究对装配线的平衡问题进行分析研究,并通过实际企业状况对装配线的平衡问题进行优化[2]。李锋等采用多种群GA算法对已定工位下装配线的生产节拍(CT)、工序分配(K)、工位负荷均衡(SI)、装配线平衡率(Eb)进行求解[3]。装配线上的工作任务由多个独立不同工作要素组成,这些要素的执行顺序受到工艺流程的要求限制。装配线必须按照规定的生产率进行运作,使得循环周期缩短并达到稳定的平衡率[4-5]。张惠等以机械式排种器为研究对象,对其装配线中工艺流程的改善、工位的划分及准时制物料配送方案进行研究,建立JIT物料配送数学模型,并使用Lingo软件求出最佳配送路径[6]。该过程中需要解决装配线工作要素的分配问题,这直接影响优化资源配置,减少装配线的空闲时间,提高平衡率。在现实企业中,随着企业规模的增大,装配线也随之扩大,其中的工作元素也会变得复杂,最终会导致装配线平衡状况和设备利用率急速下降[7-8]。因此,为了避免装配线平衡率下降、成本浪费现象的出现,本文将运用最大化候选原则、Kilbridge&Wester法和数学建模并且运用Lingo求解的方法[9]探究该问题。
1 电子仪器装配线问题
一条单一产品装配线上生产一种小型电子仪器,该产品的工作元素见表1。

表1工作元素
依据表1工作要素作前向次序图(图1),节点表示工作要素,箭头表示工作要素的顺序,每个节点上方数值为工作要素的时间。
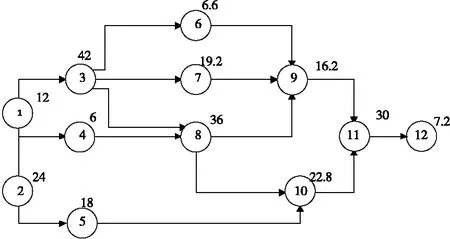
图1前向次序图
2 线平衡算法

2.1 最大候选规则

图2最大候选原则分配工作元素
2.2 Kilbridge&Wester法
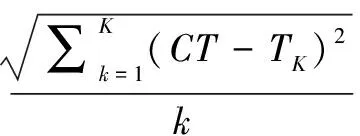

图3Kilbridge&Wester法分配工作元素
2.3 数学建模
从建立模型到最终的求解模型过程就是从实际企业或具体的情境中抽象数学问题,用数学符号建立方程式、不等式或函数等数量关系[9]。但模型中需要进行几个基本假设:(1)假设装配线中没有缓冲区,人员充足;(2)研究对象是一条固定节拍,固定工位数的连续装配线;(3)任何一个工序都必须符合优先关系顺序,当所有前顺序工序完成后,后续工序才可以开始操作;(4)每个独立的工序只能在一个工位上,不能重复多个工位;(5)在特定每一刻,工位中只能有一个工序在操作。给定的参数如下:
Tasks:Tasks={1,2…12}作业集合。
N:作业元素的个数;
i、j:作业元素的序号(指标),表示作业元素i、j;i、j=1,2…12。
ti:第i个作业元素额定时间,i=1,2…12。
Pred:作业元素的优先关系集合,Pred=i,j|作业元素i是作业元素j的紧前作业这里无需假设优先关系图中有一个唯一的终点。
K:给定的工作站数,k为工作站位的序号(指标),表示第k个工作站,k=1,2,..K。
决策变量:xik为0-1变量,当作业元素i被分派到第k个工作站是xik=1,否则为0。
CT:装配线的节拍,实数。
约束条件:
目标函数:min=CT
(1)
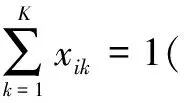
(2)
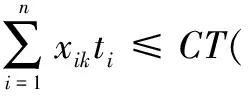
(3)

(4)
K=1,2…5;i,j=1,2…12
(5)
(6)
依据约束条件和目标函数,利用lingo11.0软件在window10平台,处理器Intel(R)core(TR)i5-4258U WCPU@2.4 GHz,64位操作处理器,进行优化求解,图4为运行结果,Lingo11.0运行程序:
model:
SETS:
TASK/1..12/:T;
PRED(TASK,TASK)/1,2,3 1,4 1,4 2,5 2,6 3,7 3,8 3,8 4,9 6,9 7,9 8,
10 8,10 5,11 9,11 10,12 11/;
STATION/1..5/;
TXS(TASK,STATION):X;
ENDSETS
DATA:
T=0.2 0.4 0.7 0.1 0.3 0.11 0.32 0.6 0.27 0.38 0.5 0.12;
enddata
@FOR(TASK(I):@SUM(STATION(K):X(I,K))=1);
@FOR(PRED(I,J):@SUM(STATION(K):K*X(J,K)-K*X(I,K))>=0);
@FOR(STATION(K):@SUM(TXS(I,K):T(I)*X(I,K))<=CyCTime);
MIN=CYCTIME;
@FOR(TXS:@BIN(X));
END
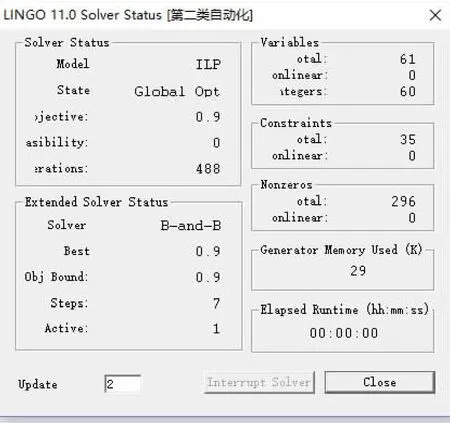
图4运行结果图
在Lingo11.0的环境下,求解模型得到全局最优解,求解目标函数为54 s,比之前的60 s减少6 s。同时通过对程序运行结果工序分配的分析,可得图5工位分配图:

图5Lingo求解工位分部图

3 结束语
本文结合某电子元器件装配线,通过运用最优候选法、Kilbridge&Wester法以及数学建模的方法对工作元素分配的工位计算平衡率、平滑指数以及节拍,进行对比发现利用数学建模与Lingo联用的方案比较优化,详细对比见表2。

表2三种线平衡法参数对比
虽然数模建模与Lingo求解最优,但是由于线性规模存在一定局限性,本文只研究了在一定条件下的单一目标求最优解情形。下一步研究需要利用其它计算方法辅助以弥补该线性问题的局限性,求解更多目标的装配线平衡问题。
[1] 刘俨后,左敦稳,张丹.随机作业时间的装配线平衡问题[J].计算机集成制造系统,2014,20(6):1372-1378.
[2] 张晓玲.装配线平衡问题不同算法性能比较研究—以H厂涡轮增压器装配线为例[D].衡阳:南华大学,2016.
[3] 李锋,邢静忠,刘伟.基于多种群遗传算法的装配线平衡问题研究[J].四川理工学院学报:自然科学版,2015,28(2):30-38.
[4] 郭湛皓.基于精益生产的手机装配线平衡研究与应用[D].南昌:南昌大学,2012.
[5] 徐发平,唐秋华,刘海.基于分枝定界法的装配线第一类平衡问题研究[J].机械设计与制造,2012(2):204-206.
[6] 张惠,李成松,李玉林,等.基于准时制物料配送的机械式排种器装配线规划研究[J].制造业自动化,2015,37(8):103-107.
[7] 吴隆,余海明,吴媛媛.基于LINGO汽车装配线平衡与研究[J].工业工程与管理,2008(6):74-107.
[8] 陈心德.生产运营管理[M].北京:清华大学出版社,2005.
[9] 谢金星.优化建模与LINDO/LINGO软件[M].北京:清华大学出版,2015.
[10] 彭运芳,高雅,夏蓓鑫.不确定条件下基于遗传算法的作业车间调度问题研究[J].上海大学学报:自然科学版,2016,22(6):793-803.
[11] 殷旅江,何波,杨立君.多类指派约束下汽车总装装配线平衡优化[J].制造业自动化,2014,36(12):41-44.
[12] 杜运普,杨月新.装配生产线的平衡问题研究[J].机械设计与制造,2003(2):104-106.
[13] YUAN B,ZHANG CY,SHAO XY.An effective hybrid honey bee mating optimazationalgorithm for balancing mixed-model two-sided assembly lines[J].Computers & Operations Reseaech,2015(53):32-41.
[14] CHUNGC L,SHIN W L,KUO C Y.Minimizing worst-case regret of makespan on a single machine with uncertain processing and setup times[J].Applined Soft Computing,2014,23:144-151.
[15] KILBRIDGE M,WESTER L.A Heuristic Method of Assembly Line Balancing[J].Journal of Industrial Engoneering,1961,12(6):292-298.
Research on the Distribution of Working Elements in the Assembly Line and Its Balance Rate
GAOZhenhao1,SUGuiying1,LIYanhua1,YUYanwei2
(1.School of Economics and Management Innovation Research Center,North University of China,Taiyuan 030051,China; 2.School of Management ,Tianjin University of Technology, Tianjin 300387,China)
With the rapid development of information age, China’s electronic products in the times with the times, the market demand for a large number of orders led to overloading the enterprise assembly line, along with the assembly line “bottleneck” phenomenon. In order to solve the problem of assembly balance, the previous heuristic station allocation method is used, but failed to achieve the optimal state. So the maximization candidate principle and the Kilbridge& Wester method are used to arrange the work elements, and then Lingo11.0 is used to solve the construction of the mathematical model of the balance rate, smoothness index and beat. Andthe balance rate, smoothness index and beat are compared to find the effect to the entire assembly line balance rateof the three elements between the different arrangements, and toconstructthe mathematical model with higher equilibrium rate. Through the analysis of electronic equipment assembly line, the validity of the mathematical model is provento meet the requirements of the process, and the solution can effectivelysolve the problem of its assembly line balance.
working elements; balance rate; maximization of candidate principles; Kilbridge & Wester method
1673-1549(2017)06-0088-05
10.11863/j.suse.2017.06.016
2017-09-25
山西省回国留学人员科研资助项目(2014-056);山西省留学回国人员科技活动择优资助项目(941303);山西省社会科学基金项目(201510ZB06);中北大学第十三届研究生科技立项项目(20161364)
高振豪(1989-),男,河南鹤壁人,硕士生,主要从事供应链管理与精益生产方面的研究,(E-mail)zhenhaogaozhenhao@outlook.com
苏贵影(1968-),女,福建永春人,副教授,主要从事系统工程与区域创新方面的研究。
TH166;F242
A
