基于纵横波速度的致密砂岩气层定性识别与定量计算方法研究

张丽华，潘保芝，单刚义，雷 健.

(吉林大学地球探测科学与技术学院，吉林长春 130026)

基于纵横波速度的致密砂岩气层定性识别与定量计算方法研究

张丽华，潘保芝，单刚义，雷 健.*

(吉林大学地球探测科学与技术学院，吉林长春 130026)

利用声学资料定量计算含气饱和度一直是学者们探讨的问题。本文参考地震勘探中纵横波资料的应用方法，通过综合应用密度测井得到的地层密度，以及阵列声波测井得到的纵横波数据，对致密砂岩储层的流体性质进行定性识别和定量计算含气饱和度，得到的结果与已有的试气结论是一致的。本文提出的计算含气饱和度的新方法，与常规电测井确定含气饱和度方法相结合用于含气储集层的解释与评价，可以提高解释准确性。

阵列声波测井；含气饱和度；气层识别；纵横波速度；骨架模量

含气饱和度是油气勘探和开发中需要确定的一个重要参数。在测井评价中,通常用各种电测井计算含气饱和度。气层的定性，主要是应用电阻率、自然电位、自然伽玛、声波、中子和密度等测井资料来识别。应用地震资料识别地层中的流体是储层预测的一项重要内容。在地震勘探中，人们通常综合利用地震纵波和横波资料来反映储层流体信息，提出了识别流体性质的多种方法[1-6]，如流体因子法、阻抗法等。普通声波测井只能得到纵波时差数据。随着科学技术的发展，声波测井探头、声波激发和接收方式都有了很大进步，发展了阵列声波测井仪，通过记录多条曲线进行相关和叠加处理，可以有效地压制干扰，准确提取纵波、横波和斯通利波的各种信息。利用声学资料定量计算含气饱和度一直是学者们探讨的问题。这不仅是测井评价的需求，也是应用测井资料和地震资料综合评价储层的需要[7]。

在测井中，预测储层流体性质是储层评价的一项重要内容。由于苏里格气田致密砂岩储层具有低孔隙度、低渗透率、复杂孔隙结构等特点，利用常规测井资料对储层含气性进行有效评价很难，因此，通常利用电阻率测井资料计算含水饱和度，从而判断油气水层。本文从地震勘探中纵横波资料的应用方法中得到启发，通过综合应用密度测井得到的地层密度和纵横波数据，对苏里格气田致密砂岩储层的流体性质进行定性识别和含气饱和度定量计算，为应用电阻率资料计算含水饱和度判断油气水层提供了一种辅助手段。

1 基于纵横波的定性识别方法

1.1 纵横波时差比法

把地层完全被水饱和时的纵横波速度比值作为背景值，在储层中，气的存在将引起纵横波速度比的减小。当纵横波速度比的测量值小于背景值时，指示气层；若两者比较接近，则指示非气层[8]。纵横波时差比DTSC定义为：

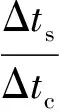
(1)

式中DTSC——纵横波时差比；

Δtc——纵波时差，μs/m；

Δts——横波时差，μs/m。

1.2 体积压缩系数法

由阵列声波测井得到的纵横波速度(vp、vs)及补偿密度测井数据ρc，可以计算岩石体积弹性模量(K)和体积压缩系数(C)：

(2)

(3)

式中vp——纵波速度，m/s；

vs——横波速度，m/s；

ρc——补偿密度测井数据，g/cm3；

K——岩石体积弹性模量，MPa；

C——岩石体积压缩系数，MPa-1。

1.3 泊松比法

计算泊松比的公式为：

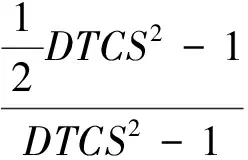
(4)

式中POSB——泊松比。

由以上公式可以看出：由于气的存在，体积压缩系数会增大，泊松比会减小，纵横波时差比也减小。

1.4 纵波弹性模量差比法

岩石的等效弹性模量变化反映了岩石孔隙流体性质的变化。在岩性和孔隙度相同的储层，当孔隙里含气时，由于纵波时差变大和体积密度变小，使得纵波等效弹性模量也变小；当孔隙里含水时，由于纵波时差变小和体积密度变大，相应地纵波等效弹性模量也变大[9]。

岩石的纵波等效弹性模量计算公式如下：

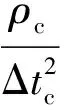
(5)

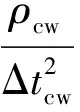
(6)

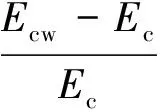
(7)

式中Ec——储层的等效弹性模量，10-5N/cm2；

ρc——储层的密度，g/cm3；

Ecw——储层完全含水时的等效弹性模量，10-5N/cm2；

ρcw——储层完全含水时的密度，g/cm3；

Δtcw——储层完全含水时的纵波时差，μs/m；

DR——纵波等效弹性模量差比值。

如果DR大于零，则指示气层。这里计算岩石的等效弹性模量，不用计算岩石的泊松比；在没有横波测井资料时，也可以使用。

2 基于Biot-Gassmann理论的定性识别与定量计算

岩石是有孔隙的矿物的集合体。孔隙空间中充填有一种或多种流体，当波在岩石中传播时，矿物骨架会发生变形，孔隙中的流体也会压缩、伸展或是流动。基于Biot-Gassmann[10-11]理论和关系，纵波速度vp和横波速度vs的计算公式如下：

(8)

(9)

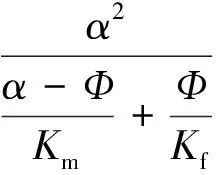
(10)

式中Kb——颗粒骨架的润湿体积量，GPa；

N——颗粒骨架的剪切模量，GPa；

Kp——孔隙空间模量，GPa；

Km——岩石骨架的体积模量，GPa；

Kf——流体的体积模量，GPa；

α——柔量；

Ф——孔隙度，%。

W.MURPHY[12]收集了很多砂岩样品试验数据，包括岩样的孔隙度，饱含气时的纵波速度、横波速度，以及饱含水时的纵波速度、横波速度。根据试验数据得出了由气饱和岩样的速度计算骨架模量的公式。图1和图2分别是骨架剪切模量和骨架体积模量与孔隙度的关系图，从图中可以看出，骨架模量随着孔隙度的增大而减小，骨架模量与孔隙度具有明显的相关性。

(11)

(12)

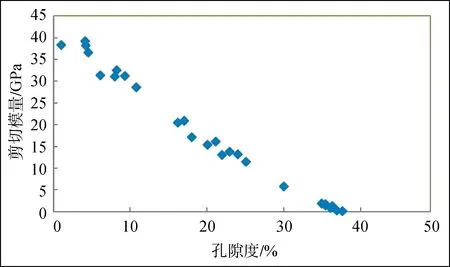
图1 骨架剪切模量与孔隙度关系Fig.1 Relationship between matrix shear modulus and porosity

图2 骨架体积模量与孔隙度关系Fig.2 Relationship between matrix bulk modulus and porosity

定义

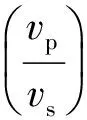
(13)

计算孔隙空间模量Kp的公式是：

(14)

流体的体积模量Kf的表达式为：

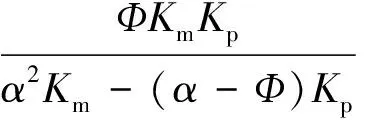
(15)

Km是岩石骨架的体积模量，对于砂岩，Km取44 GPa。

α是柔量，由下式计算：

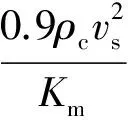
(16)

Brie[13]在比较视流体模量与通过测井方法计算的冲洗带流体饱和度之后，拟合出一个经验公式：

(17)

由此可推出定量计算含气饱和度Sg的公式：

(18)

式中Kg——气的体积模量，0.1 GPa；

Kw—— 水的体积模量，2.2 GPa；

Kfa——视流体体积模量，GPa；

Sxo——冲洗带含水饱和度。

e——常数，对于砂岩，e=3。

3 应用实例

鄂尔多斯盆地存在大面积低丰度岩性气藏，其中苏里格气田是迄今为止我国陆上发现的最大天然气田，是低渗透岩性气藏的典型代表。苏里格地区测井储层评价仍面临的主要问题为：一是致密砂岩气层的孔隙度低和渗透率低，准确识别气层难度大；二是致密砂岩气层孔隙结构复杂、含气饱和度低，气水关系复杂，流体定量评价困难。在研究中，选取研究区有纵横波测井资料的三口井，将以上方法运用Fortran语言编程，挂接在Forward平台上形成模块，对实际井资料进行了处理。

在以下各图中，vp、vs是通过测井纵横波时差计算得到的速度，(vp/vs)2指的是纵横波速度比的平方，标有“预测”的vp指的是通过横波速度计算的纵波速度，标有“预测”的其余各量是通过本文的相应公式计算得到的。Sw是常用的应用电阻率测井资料计算的含水饱和度，Sg是本文应用纵横波资料计算的含气饱和度。

图3是A井某井段的处理成果图。在3655.4～3658.4 m层段从泊松比与体积压缩系数的镜像来看，有气显示；纵横波速度比低于背景值1.6；纵波等效弹性模量差比值大于0，显示气；计算的纵横波速度比的平方接近于理论气线；预测的纵波速度与计算的气层纵波速度接近，而偏离水层的纵波速度线；计算的孔隙流体体积模量很小，接近于0；计算的含气饱和度Sg平均为60%，Sw平均为40%。综合这些结果，将该层解释为气层。该层测试日产气46849 m3，测试结论为气层。解释结论与测试结果一致。

图3 A井某井段处理成果Fig.3 The results of an interval of well A

图4 B井某井段处理成果Fig.4 The results of an interval of well B

图4是B井某井段的处理成果图。在3461.0～3465.6 m层段从泊松比与体积压缩系数的镜像来看，有气显示；纵横波速度比稍低于背景值1.6；纵波等效弹性模量差比值大于0，显示气；计算的纵横波速度比平方接近于理论气线；预测的纵波速度与计算的气层纵波速度和水层的纵波速度线都接近；计算的孔隙流体体积模量很小，接近于0.6；计算的含气饱和度Sg平均为45%，Sw平均为60%。综合这些结果，将该层解释为含气水层。该层测试日产气5096 m3，日产水23 m3，测试结论为含气水层。解释结论与测试结果一致。但是，在3459.5～3460.6 m层段，依靠电阻率资料计算的含水饱和度Sw为22%，如果仅仅依靠电阻率资料计算的Sw来确定储层性质，该层应判为气层，但依据Sg判断，该层应为水层。综合来看，这一层不能被判为气层。

图5是C井某井段的处理成果图。在3613.0～3614.6 m层段，从泊松比与体积压缩系数的镜像来看，有气显示；纵横波速度比稍低于背景值1.6；纵波等效弹性模量差比值接近于0；计算的纵横波速度比平方接近于理论气线；上部预测的纵波速度与计算的气层纵波速度接近，下部预测的纵波速度与计算的水层纵波速度接近；计算的孔隙流体体积模量上部接近于0，下部为2.0；计算的含气饱和度Sg平均为62%，Sw平均为40%。综合解释该层为气水同层。该层测试日产气36160 m3、日产水4.5 m3，测试结论为气水同层。解释结论与测试结果一致。

图5 C井某井段处理成果Fig.5 The results of an interval of well C

此外，从以上各图中还可以看出，在砂岩层段，计算的纵横波速度比的平方与预测的纵横波速度比的平方几乎一致；而在泥岩层段，二者却有明显的差别。在泥岩层段计算的剪切模量与预测的剪切模量之间的差异会明显增大。这两个区别砂岩和泥岩的标志与自然伽马曲线指示的岩性是一致的。

4 结论

(1)通过应用阵列声波测井得到的纵、横波速度，以及密度测井得到的地层密度，得到了利用纵横波速度比、体积压缩系数、泊松比、纵波弹性模量差比法等定性识别致密砂岩气层的方法，如果纵波弹性模量差比大于零，则指示气层。体积压缩系数增大、泊松比减小、纵横波时差减小，也是气层的指示标志。

(2)通过计算孔隙流体体积模量、理论气线的纵横波速度比的平方、气层纵波速度线和水层的纵波速度线，与预测的相应值对比，也可定性识别气层。通过公式定量计算含气饱和度，对定性识别出的气层有一个量的概念。研究方法得到的结果与测试的结论是一致的。定性识别与定量计算方法在致密砂岩中取得了满意的效果，对其他岩性的储层有参考意义。

(3)本文丰富了声波测井资料在储层评价中的应用，提出了含气饱和度计算的新方法。新方法与常规电阻率测井方法确定含气饱和度相结合，用于含气储集层的解释与评价，进一步提高了解释准确性。

[1] 宁忠华,贺振华,黄德济.基于地震资料的高灵敏度流体识别因子[J].石油物探, 2006,45(3):239-242.

[2] GOODWAY W, CHEN T, DOWNTON J. Improved AVO Fluid detection and lithology discrimination using Lame petrophysical parameters from P and S inversion[J]. Expanded Abstracts of 68th Annual Internat SEG Mtg, 1997:183-186.

[3] RUSSELL B H, HEDLIN K, HILTERMAN F J, et al. Fluid Property discrimination with AVO: A Biot-Gassmann perspective[J]. Geophysics, 2003,68(1):29-39.

[4] DILLON L, SCHWEDERSKY G, GUILHEMER V, et al. A multiscale DHI elastic attributes evaluation[J]. The leading Edge, 2003,22(10):1024-1029.

[5] 陈遵德,朱广生.地震储层预测方法研究进展[J].地球物理学进展,1997,12(4):76-84.

[6] 刘文玲,牛彦良,李刚,等.多信息储层预测与地震属性提取与有效性分析方法[J].石油物探,2002,41(1):100-106.

[7] 刘国强,谭廷栋.孔隙度和含气饱和度的弹性模量计算方法[J].石油勘探与开发, 1993,20(5):33-41.

[8] 张丽华,潘保芝,单刚义,等.长岭地区火山岩储层流体性质测井预测[J].地球物理学进展,2009,24(6):2151-2155.

[9] 谭廷栋.用等效弹性模量差比法识别裂缝性气层[J].天然气工业,1985(1):12-20,5.

[10] WILLIAM M, ANDREW R, KAI H. Modulus decomposition of compressional and shear velocities in sand bodies, GEOPHYISCS, 1993,58(2):227-239.

[11] BRIE A,PAMPURI F, MARSALA A, et al.. Shear sonic interpretation in gas-bearing sands[A]. SPE30595,1995.

[12] BIOT M A. Theory of propagation of elastic waves in a fluid saturated porous solid. I. low frequency range. II. Higher-frequency range[J]. Acoustics Society of America,1956,28(2):168-178.

[13] GASSMAMM F. Uber die Elastizitat poroser Medien, Vierteljahrsschrift der Naturforschenden Gesellschaft in Zurich[J]. 1951,96:1-23.

ResearchonGasZoneIdentificationandComputationinTightSandBasedonCompressionalandShearWaveVelocity

Zhang Lihua, Pan Baozhi, Shan Gangyi, Lei Jian

(CollegeofGeo-ExplorationScienceandTechnology,JilinUniversity,Changchun,Jilin130026,China)

The use of acoustic data of quantitative calculation of gas saturation has been studied by researchers. Referencing the application methods of P- and S-wave in seismic exploration, this paper synthesized the formation density from density log, and the P- and S-wave from array sonic logging to qualitatively identify fluid property and quantitatively compute gas-bearing saturation. The computational results were accordant with the gas testing results. A new method for calculating gas-bearing saturation was proposed, which can improve the accuracy rate of the interpretation and evaluation of gas bearing reservoir by combining the method with the conventional electrical logging.

array sonic log; gas-bearing saturation; gas-bearing identification; P- and S-wave velocity; matrix modulus

张丽华(1974—)，女，博士，高级工程师，主要从事岩石物理与测井数据处理与解释研究工作。邮箱：zhanglh@jlu.edu.cn.

单刚义(1970—)，男，博士，高级工程师，主要从事地震数据处理与解释研究工作。邮箱：shangangyi@jlu.edu.cn.

P631.8

A