车间内多周期混合收送货物流调度优化研究

，

(浙江理工大学，a.理学院；b.经济管理学院，杭州 310018)

车间内多周期混合收送货物流调度优化研究

韩曙光a，季园园b

(浙江理工大学，a.理学院；b.经济管理学院，杭州 310018)

从精益物流角度出发，生产车间的停线待料、成品堆积、车辆堵塞等增加了生产线成本，传统的收货与送货存在严重的资源浪费。在混合收送货的基础上重点研究了循环供料及周期间的关系，建立了装配车间考虑时间窗的多周期混合收送货物流调度模型，并以S公司电动工具装配车间为例，分别用单周期优化模型和多周期物流调度优化模型求解，利用Lingo编程计算给出具体调度方案，将两种方案进行对比，结果表明多周期调度方案更优，可进一步降低装配车间的成本。

精益物流；混合送收货；时间窗；多周期

精益是一种体系化的工具也是一种生产方式，它通过小批量大批次的生产，减少一切浪费，以此提高客户满意度。精益首先被丰田汽车验证是成功的，在那之后的二十多年里，精益几乎被所有知名的制造企业学习以及模仿，但是从生产现状看，精益的道路只能说是刚起步，距离尽善尽美还很遥远，而在物流这一方面，成熟度更低。为了降低成本，提高企业竞争力，越来越多的制造商将精益生产与理论用于实践。精益物流在实施过程中除了有很多原则要遵循以外，还有很多物流工具，如拉动、直送上线、循环供料等。循环供料是精益物流在实施过程中最重要的工具之一，主要指仓库为了满足各生产线需求，进行循环配送，在固定的时间将固定数量的物料依次供给各条生产线。这种配送方式虽然增加了运输频次，但是加快了物料流动速度，降低了生产线库存面积并改善了生产现场[1]。因此在生产装配车间中，仓库如何合理安排车辆为生产线进行循环供料，对于生产线正常生产，控制线边库存、降低成本意义重大，国内外许多学者对物料配送、车辆调度、以及多周期问题进行了广泛的研究。

物料配送方面，蒋丽等[2]研究了生产车间以工位为中心的优化问题，建立了以配送时间最小为目标的物料配送模型；丁佳祺等[3]研究了汽车生产物流中从物料超市到生产线的物料供应；李佳玲等[4]结合多品种小批量的特征，研究了工位需求时间不确定的物料配送问题，建立了有时间窗限制的物料配送模型；韩曙光等[5]以总成本最小为目标，综合考虑了工位服务时间窗，最小线边库存，建立了物料配送模型；Gajpal等[6]用一个蚁群系统求解车辆路径问题中的同时送货和取货问题；洪旭东等[7]通过研究看板的物料循环配送模式、物料循环配送的流程，建立了循环式的物料配送模型，并实现库存成本最低；葛茂根等[8]研究了机械装配中的物料配送问题，以配送成本、配送时间和线旁库存为目标建立优化模型；Boysen等[9]研究了配送中心配送的准时性问题，利用信息系统并以线边最高库存最小为目标，建立了准时制配送模型；Fathi等[10]研究了装配线的优化问题，以库存和配送次数为目标建立了混合整数线性规划模型。

在实际生产过程中，仓库在收到生产线服务信息后，需要及时安排车辆按固定的路线给各条生产线进行配送。因此车间内的配送问题也是一种特殊的车辆调度问题，受到国内外学者的高度关注。Dantzig等[11]研究了加油站之间的一组加油车辆的最优路线问题，这标志着车辆路径问题的诞生，之后对车辆调度问题的研究主要集中在取送需求、车辆装载能力、车辆-车场关系、时间窗等方面；Mosheiov 等[12]率先提出了带有取送货的旅行商问题，以行驶路程最短为目标建立优化模型；Gulczynski等[13]为了降低多台车为客户服务导致各项成本的增加，建立了对取送任务进行分割的车辆调度模型；杨仁法等[14]研究了配送中心车辆调度问题，建立了带有时间窗惩罚的以运输成本最小为目标的车辆调度模型；蒋欢欢等[15]为了解决成品堆积的问题，建立了生产车间混合收送货的车辆调度模型；韩敏等[16]为了实现汽车制造厂多批次、小批量配送效率的提高，建立了以运输时间和距离为约束的车辆调度优化模型；朱玲等[17]以需求可拆分为前提，建立了以最小库存和运输成本为目标的路径优化模型；李杨等[18]研究了汽车零部件入厂物流循环取货问题，合理安排车辆数量及行踪，使总成本最小。

目前对于多周期问题的研究也很少。宋志华等[19]深入研究了导弹作战行动规划问题，根据作战问题的多阶段性建立了动态规划模型，并通过算例说明此模型可为大规模多波次导弹问题的求解提供支持；王梓行[20]等主要研究了两个周期的导弹发射问题，从仓库到发射点的第一轮射击、再到配送中心装弹、到射击点位进行第二次射击的三个过程，以总暴露时间最短为目标，分别对三个阶段建模，充分考虑了每个阶段之间的时间以及起始点之间的关系。

以上研究多以物料配送、单周期调度为主,关于多周期调度的研究较少。本文以装配车间生产物流为研究对象，在解决生产缺料、成品堆积的基础下，考虑了生产实际的连续性，在蒋欢欢[15]的研究基础上，以循环配送为研究重点，考虑了各生产环节之间的衔接过程，对多周期的车间物流进行了优化。两者在处理一个周期时并没有明显的区别，但循环配送时，文献[15]中将前一个周期的优化结果作为后一个周期的已知条件；而本文的多周期模型只要计算一次就可求出总成本，最后以S公司装配车间两个周期订单为例，分别用两调度模型求解并对比分析而得出结论。

一、问题提出及车间混合收送货流程分析

(一)问题提出

在装配生产车间，首先物料计划员根据客户需求安排生产计划，将生产计划以白卡订单的形式交给生产线，生产线通过扫描看板将需求信息发送给仓库，仓库拣货人员负责将各生产线所需物料捡好放在平板车上，待牵引车回到仓库后将物料拖走[15]。然而在实际操作当中由于各种突发状况，导致仓库送料不及时，成品堆积严重，各项成本增加，主要原因如下：

a) 员工凭经验处理问题。仓库配送人员凭经验判断发车时刻，判断出错时会导致送料不及时或产线缺料；生产线换型频繁，物料多而复杂，生产线物料员凭经验触发看板导致物料到达不及时或太早。

b) 生产线一般对可以堆放的成品数量有明确规定，每隔一段时间仓库配送人员会到生产线取走，当配送人员不能准时到达时，成品堆积便会超出线边区域，影响生产线的正常生产[15]。

c) 物料循环配送，车辆调度不合理，影响产线连续生产。

d) 生产线在生产过程中由于各种状况导致停线，多次循环后导致与生产计划有较大偏差，无法准时交货，会引起客户投诉，降低客户满意度。

(二)混合收送货流程分析

由文献[15]可知在传统的物料配送和成品下线过程中都存在空车现象，资源浪费严重，而且生产线之间过道面积有限，如果送料的车和取货的车碰到就会发生堵塞，因此文中采取将收送货相结合的方式解决这些问题，如图1为混合收送货流程图。

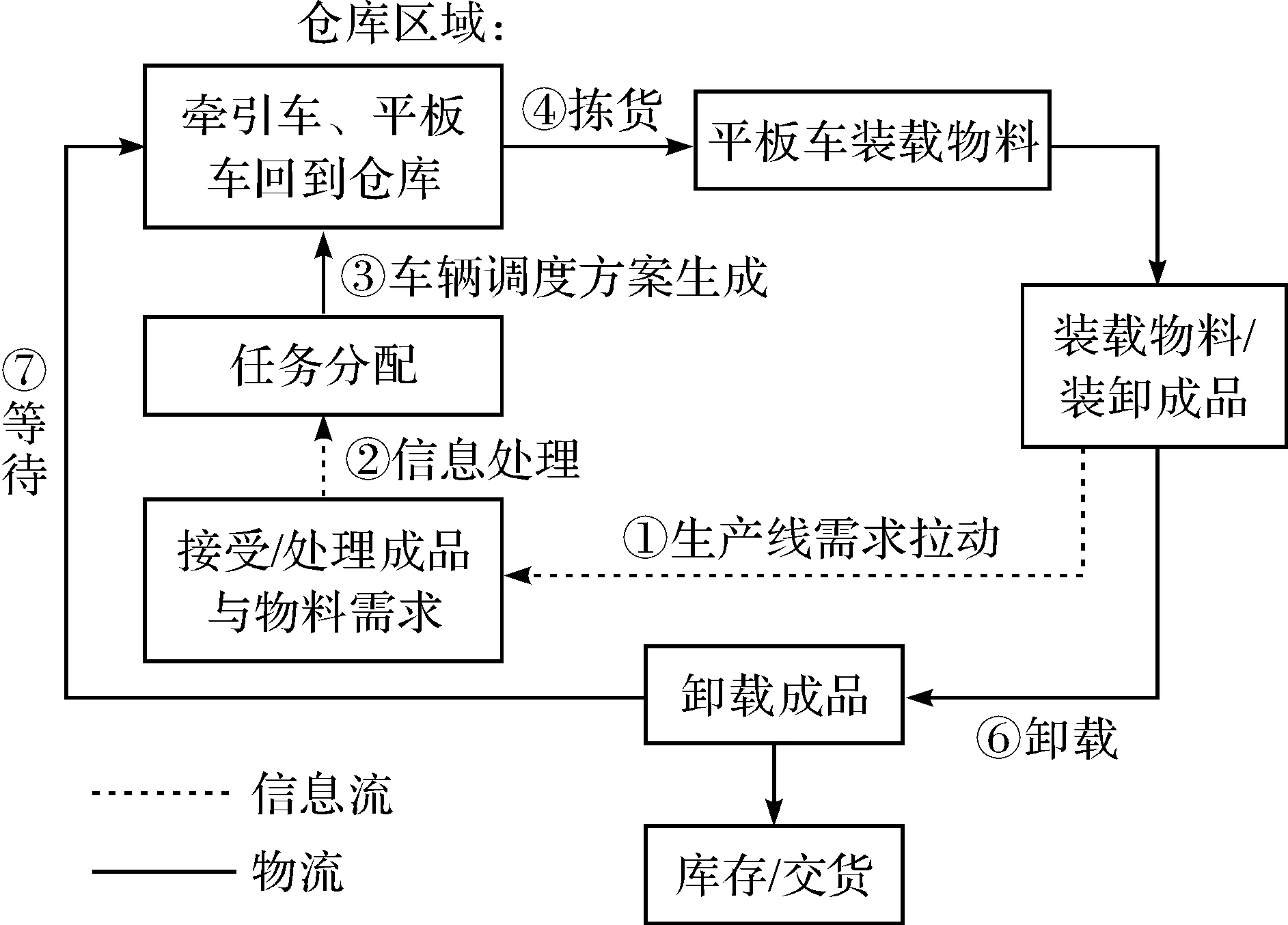
图1 混合收送货流程

然而在实际生产中，上一个周期末的库存量直接影响到下一个周期的配送时刻，消耗速度也影响下一个周期的库存剩余量,即相邻周期之间相互影响，这也是文献[15]中未完成的部分。S 公司电动工具装配车间严格要求生产线记录每小时产量，并与计划产量对比，如果出现延误，多个周期循环下来，会影响一天的生产计划。因此研究生产车间内的多周期物流调度有助于保证实际生产的连续性。

二、多周期的装配车间混合送收货物流调度问题

(一)问题描述

在对生产线循环送料和取货过程中，物料计划员为生产线排产，生产线物料员根据生产计划触发看板，电子看板将生产线所需物料名称、数量、每把工具所需数量、生产节拍、上一次离开的时刻以及上一次离开的库存量等信息传递给仓库，仓库拣货员收到生产线订单后开始拣货，装货，等待牵引车来拖走，并把订单附在物料上[15]。假设条件如下：

a) 本文所涉及的物料都使用标准物料小盒(不包括大盒物料)，物料从仓库配送至生产线线边，不考虑捡货，入库位时间；

b) 文中各产线物料消耗稳定，同一条生产线在每个周期内的需求相同；

c) 生产线在生产时都按照规定的工艺生产，为保证满足生产线需求，仓库料都充足；

d) 假设各生产线在相邻周期内生产同一种机型，仓库隔一段时间对生产线的需求信息做一次统一处理；

e) 牵引车后面可以拖若干平板车，为防止混料，假设每个平板车只为一条生产线服务；

f) 运输成本只与车辆启动次数有关，与运输的物料及成品数量无关；

g) 每张看板量满足一拖成品需求。

(二)符号说明

i：站点编号；

j：站点编号；

k：周期编号；

n：周期数；

m：站点个数；

l：配送次数；

c1：指派一辆牵引车的成本；

c2：牵引车在各站点单位时间内的等待成本；

c3：一个标准物料在生产线的存储成本；

c4：一辆平板车的使用成本；

h1：第一批订单时刻；

hk：第k批订单时刻；

Ri：站点i的物料生产节拍，及站点i对物料加工的时间；

Ni：站点i的物料看板数，即一张看板上某物料的需求数量；

Fi：做成一把工具所需要站点i的物料数量；

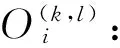
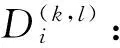
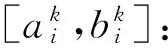
Si：在站点i的服务时间；

μi：转化为标准零件的系数；

k：平板车的数目；

g(k,l)：第k个周期l批次是否启用平板车；

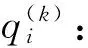
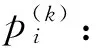
e(k,l)：第k个周期l批次是否有货物被送到；

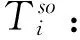
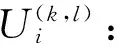
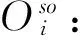
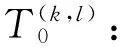
tij：站点i到站点j的时间。

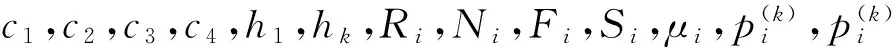
(三)车辆调度模型

以所有周期内的运输成本，各站点最高库存成本以及等待成本之和最小为目标，建立数学模型如下：

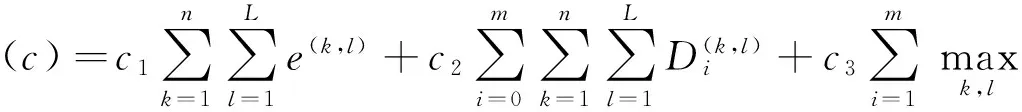
(1)

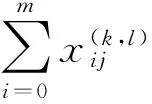
(2)

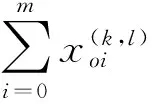
(3)

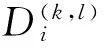
(4)

(5)

(6)

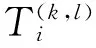
(7)

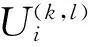
(8)

(9)

(10)

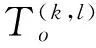
(11)

(12)

(13)

式(1)为目标函数，第一部分表示牵引车的启动成本；第二部分表示在生产线的等待成本；第三部分是线边库存成本，由于生产线线边面积有限，库存堆积影响生产线现场，缺料又会导致停线，因此要求最大线边库存最小；第四部分是平板车的使用成本，平板车的使用数量只与服务生产线数量有关；各站点之间距离可忽略不计；

式(2)表示每个周期每个批次内，服务某个站点的车和离开的车相同，满足流量守恒；

式(3)表示每个周期每个批次内，车辆都是从仓库出发并且回到仓库；

式(4)表示每个周期每个批次在站点i的等待时间；

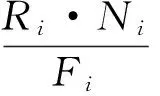
式(6)表示在第k个周期(k≥2)中对站点i的服务时间窗(取货下限为上一周期最后一批次离开的时刻加上将看板数量消耗完的时间，上限为上一周期最后一批次离开的时刻加上将看板数量消耗完的时间，再加上生产一把工具的时间；送货下限为发送需求的时刻，上限为上一周期最后离开的时刻加上将库存消耗完的时间)；

式(7)表示在第k个周期中到达站点i的时刻；

式(8)表示在第k个周期中离开站点i的时刻；

式(9)表示在第k个(k=1)周期中离开站点i时的库存量；

式(10)表示在第k(k≥2)个周期中离开站点i的库存量；

式(11)表示在第k个周期第l(l≥2)个批次中从仓库的出发时刻必须大于等于上一批次离开的最大时刻；

式(12)表示是否启动牵引车。

(四)多周期与单周期车间混合收送货物流调度模型的比较

两个模型相比，存在许多异同点。相同点表现如下：

a) 目标函数相同。都是以牵引车与平板车使用成本、库存堆积成本、等待成本最小为目标函数。

b) 两个模型在处理第一个周期时需要输入的参数变量一样。

处理多个周期时，两个模型有明显的不同：

单周期优化模型在处理多个周期时需要分步计算，一个周期计算一次。通过已知变量求出第一个周期末各产线的库存、牵引车离开时刻以及最小的成本，第二个周期的求解以第一个周期末为起点重新计算，以此类推，最后将所有周期的成本相加得出总的成本；而多周期优化模型只需将已知参数输入，就能得出最后所有周期的总成本。

综上，多周期调度优化模型求解效率更优，而且求得全局最优解，对于车间日常生产更具有实际意义。

(五)参数分析

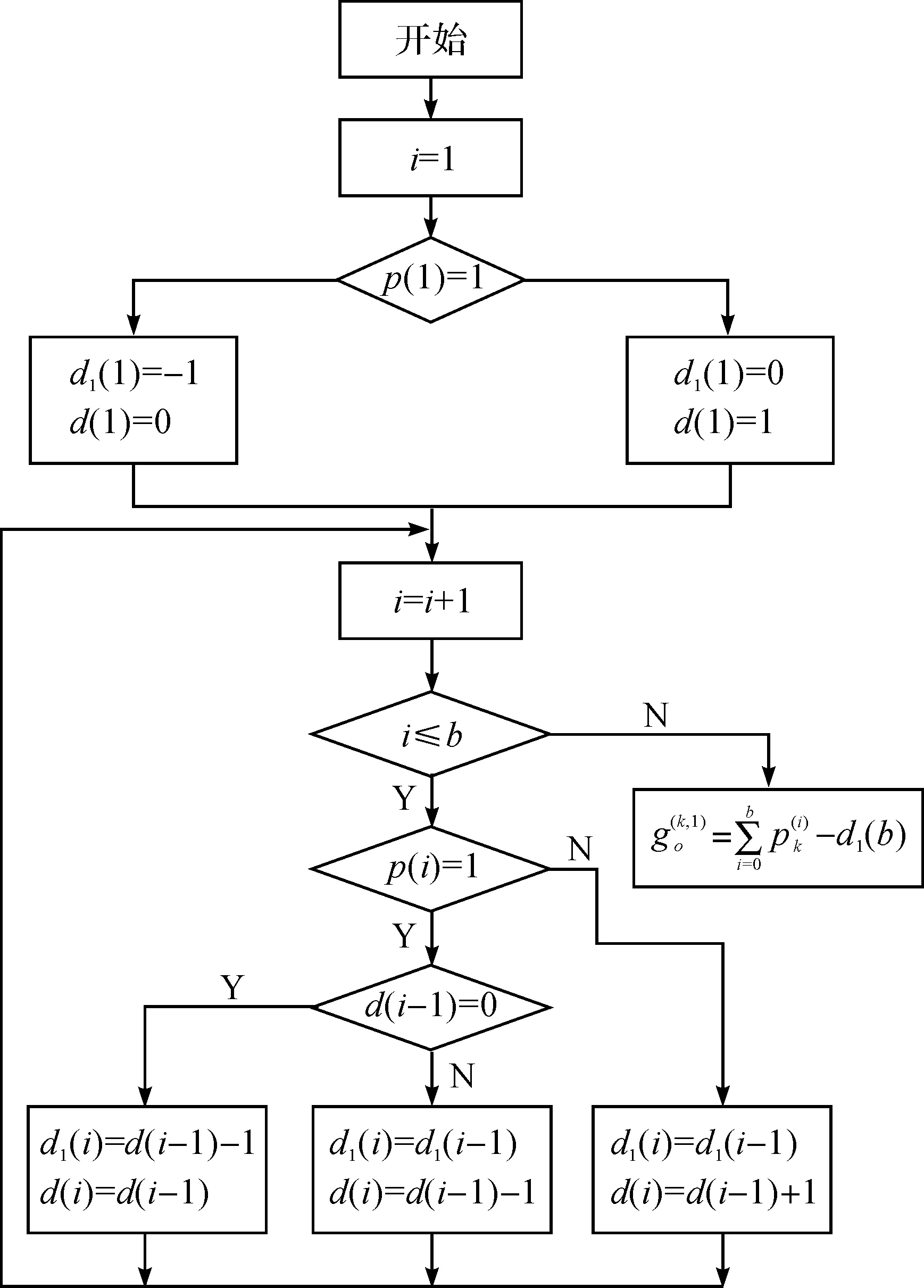
图2 每车次实际使用平板车数量计算流程图

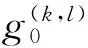
三、S公司案例分析

(一)S公司简介

S公司是德国的一家电动工具生产商，于1995年成立于杭州，占地14万平方米。其生产的电动工具包括电锤、电钻、冲击钻、角磨机、电刨和砂磨机等，适用于各种行业，而且这些产品无论在质量还是在技术上都维持着较高的标准。在S公司诞生的二十几年中，一直坚持将精益思想用于研发、生产、物流等各环节，也因此成为了中国乃至亚太最专业、质量最好、服务水平最高的电动工具企业。然而近几年由于客户需求的多样化、人民币升值，使得公司销售量增幅变小，为了重新赢得成本优势、减少浪费，公司内部在不影响正常生产的情况下进行整改，消除不必要的浪费。

(二)生产车间存在问题分析

1.物料、半成品、成品堆积严重

成品堆积在过道中间，占用了大量生产线面积，装配线旁的小车上堆满了物料，造成线边资源更少。如果成品不能及时入库，物料长时间堆积在生产线旁，会影响生产线综合评价指标，而这些指标和生产线员工以及生产工程师的绩效息息相关。

2.生产线发送需求时间不合格

生产线每个物料生产节拍固定，其看板都有固定消耗的时间，若在消耗完之前半个小时内向仓库发送信号，则此信号不合格[15]；物料员如果为了降低库存，过晚的触发看板，会导致生产线停线，此信号也不合格。如表1是某日一厂车间内生产的装配线发送需求时间合格率，达标的生产线只有12%，由此可见生产线触发看板的及时性还有待于提高。

3.生产周期之间衔接不好，无法按时完成生产计划

交货期对于生产线来说是一项重要的考核指标，关系到生产线效益评估。一般物料计划员收到客户订单后，会严格按照生产节拍进行排产，包括每小时的产量。由于生产时周期之间衔接不好，不能按时完成生产计划，最后导致交货期延迟，客户满意度差，严重的还会导致客户投诉。

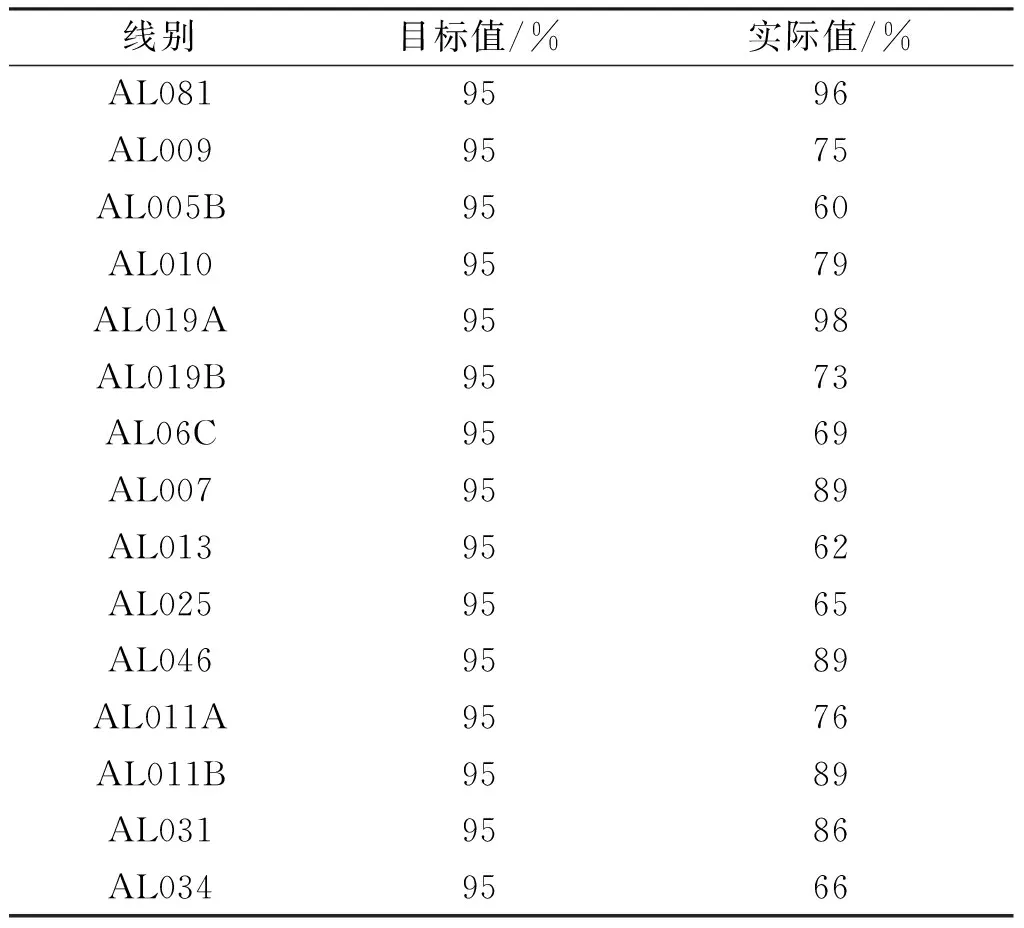
表1 装配线发送需求合格率

(三)车间多周期混合收送货物流调度优化

以S电动工具有限公司生产车间为例，运用文中的多周期物流调度模型进行求解。本文以4条产线为例(产线10、产线17、产线19、产线47)，这四条产线在这两个周期内各自生产同一种机型，每个机型每个周期需求相同，即L10连续两个周期生产机型PHO，L17连续两个周期生产机型GRO108，L19连续两个周期生产机型IX04，L47连续两个周期生产机型1996。小车从仓库出发都启用一辆牵引车，后面拖着若干平板车。仓库拣货单收到生产线订单后拣货，将物料放置在平板车上(拣货时间不计)。牵引车在每周期每个批次的启动成本均相同为2.0元/次，服务过程中牵引车在站点的平均等待成本为2.0元/分钟，平板车在每个周期每个批次的启动成本为0.3元/辆，标准零件的线边库存成本为0.6元/个[15]。牵引车在不同生产线间行驶所需要时间如表2所示。某工作日的上午仓库接收到需求信息如表3。

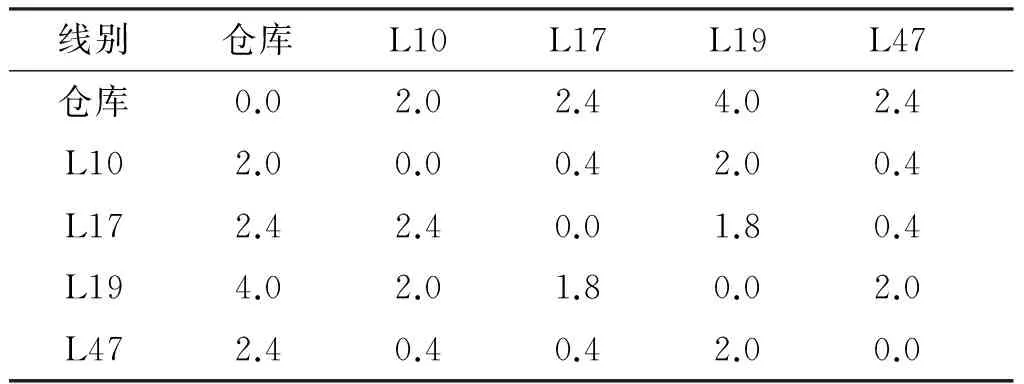
表2 不同生产线间牵引车行驶所需时间 min

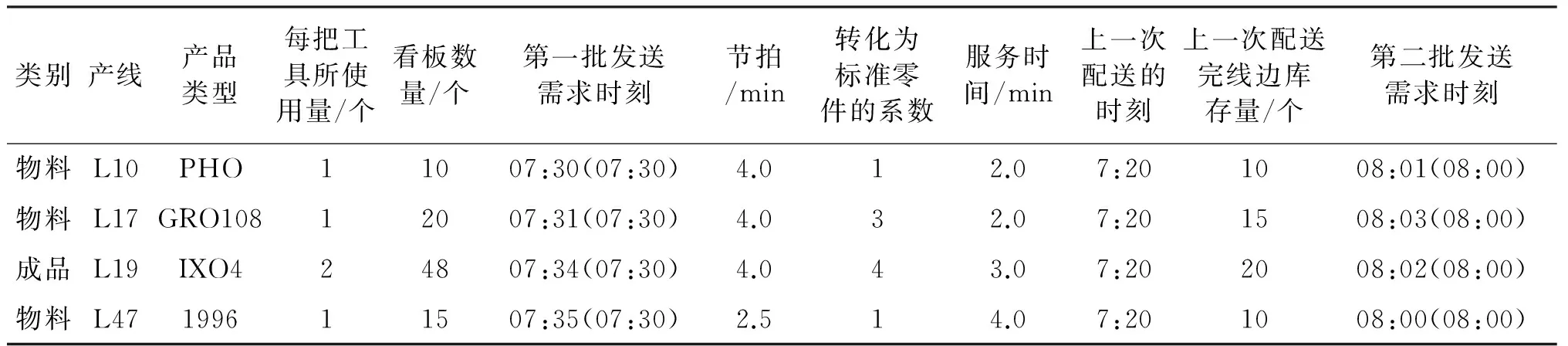
表3 生产线发送需求信息表*说明：以表中L10为例，当L10生产PHO机型时，每把工具需要某物料1个，看板数量固定为10个，每次产线发送需求时，需求数量都是看板数量，生产节拍指生产线做完一把工具所需的时间，L10生产完一把工具所需时间是4分钟，转化为标准零件的系数是利用标准零件和其他零部件填满一个A3容器数量求得，L10中物料转化为标准的系数为1。

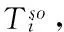
根据文献[15]单周期混合收送货模型，利用Lingo编程求解两次，调度方案如表4:第一次求解得第一周期第一车次07:51从仓库出发，07:53到L10送物料，返回仓库；第一周期第二批次07:58从仓库出发，08:00到L17送物料，08:03到L19取成品，08:06到L47送物料，回到仓库，第一周期总成本75.78元；第二周期第一批次08:27从仓库出发，先后到L10送物料，L19取成品；第二周期第二批次08:37从仓库出发，先后至L17、L47送物料，返回仓库，服务完所有的站点共用时51分钟，第二周期总成本60.96元，库存15.4个，停线0分钟。以上的两个周期总成本为136.7元。

根据已建立的多周期调度模型，用Lingo编程求解，调度方案如表5：第一周期第一车次07:29从仓库出发，先后至L17送物料，L19送取成品，L10送物料，返回仓库；第一周期第二批次07:40从仓库出发，07:43到L47送物料，回到仓库；第二周期第一批次07:56从仓库出发，07:58到L10取成品，07:59到L17取成品，08:02到L19送物料，08:05再到L47取成品，服务完所有的站点，共用时36分钟，总成本为116.47元，库存为7个，停线0分钟。

表4 单周期调度方案

表5 多周期调度方案

单周期调度方案与多周期调度方案对比如图3所示，通过图3对比可知，运用多周期物流调度模型产生的调度方案与单周期调度模型产生的方案对比，在总成本降低14.8%的基础上，总配送时间提前29.7%，线边总库存下降54.5%。因此，多周期车辆调度模型可为装配生产车间的车辆调度提供了更优的方案。

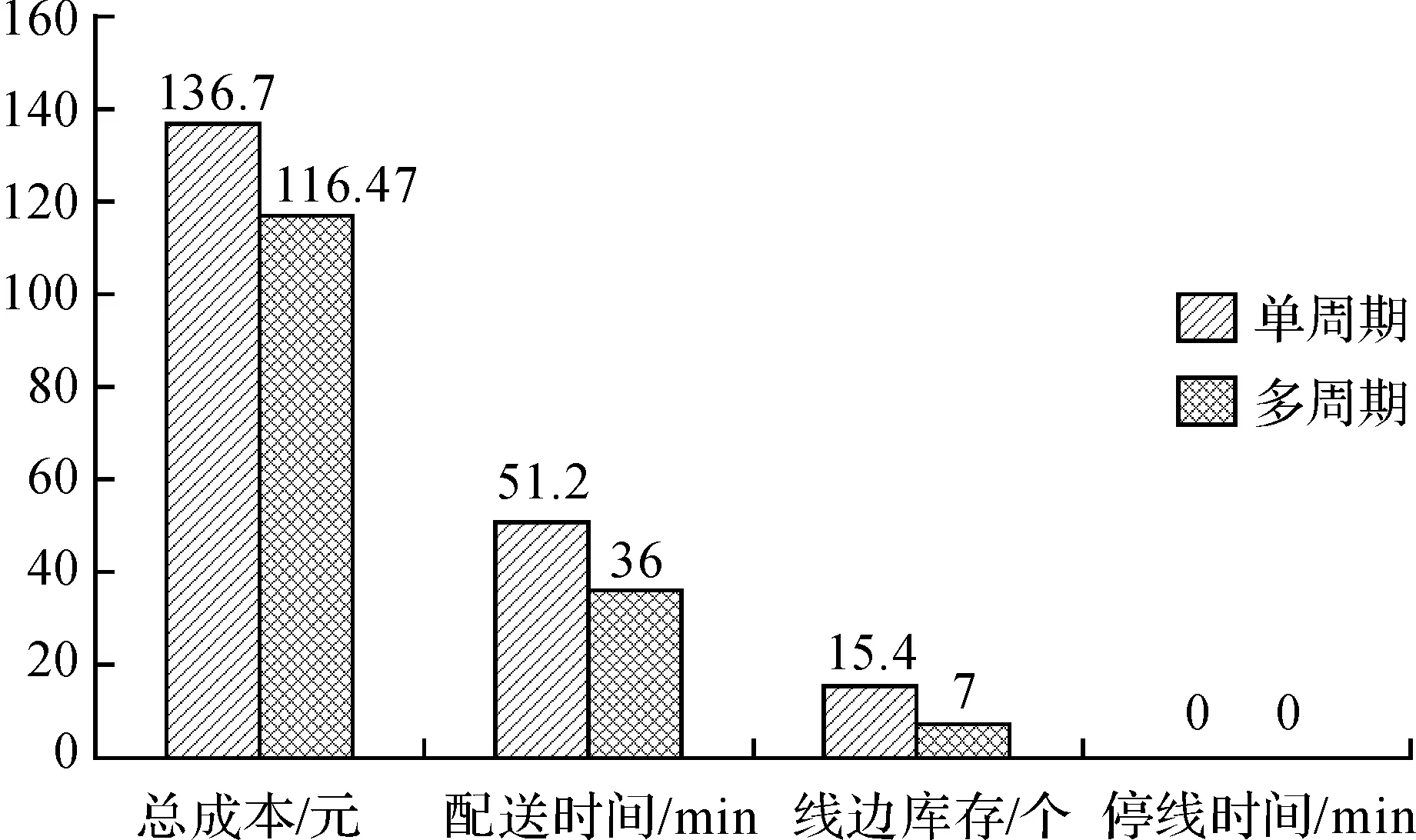
图3 单周期调度方案与多周期调度方案对比

四、总 结

本文以精益生产为着眼点，在单个周期优化的基础上，研究生产车间循环送料的车辆调度问题，充分考虑了周期与周期之间的联系，并且在满足各生产线时间窗的约束下，优化了每车次平板车的数量。最后以S电动工具有限公司生产车间为例，分析了车间存在的问题，利用已经建立的多周期物流调度模型进行优化，通过Lingo 计算结果给出具体的调度方案，并与原来单周期调度方案进行对比，验证了模型的可行性和有效性，进一步推进了精益思想在车间改进生产现场的应用，也有利于S公司提高自身竞争力。但是在算例中通过Lingo计算时发现，程序的不断调整会提高其计算的数据量，但随着生产线数量不断增大、周期不断增加，Lingo 计算时间也会加长。而在实际运用过程中，决策对时间的要求也是相当高，因此如何利用算法高效地寻找最优调度方案是后续研究的重要内容。

[1] 李震宇.精益物流实施精要[M].北京：机械工业出版社,2016.

[2] 蒋丽,丁斌,臧晓宁.以工位为中心的生产物流配送优化[J].计算机集成制造系统2009,15(11):2153-2159.

[3] 丁佳祺,张镓,蔡三发.基于看板的汽车生产物流超市物料配送优化研究[J].物流技术,2015，34(10):225-227.

[4] 李加玲,钱吴永.基于软时间窗的车间物料配送调度优化研究[J].物流技术,2016,35(12):135-140.

[5] 韩曙光,蒋欢欢,胡觉亮.基于电子看板的装配线物料配送优化研究[J].浙江理工大学学报,2017,38(2):120-126.

[6] GAIPAL Y, ABAD P. An ant colony system(ACS) for vehicle routing problem with simultaneous delivery and pickup[J]. Computers & Operations Research,2009,36(12):3215-3223.

[7] 洪旭东.基于看板的生产线物料循环配送方式[J].工业工程,2009,12(4):116-210.

[8] 葛茂根.基于JIT的多目标总装准时物料配送方法研究[J].中国机械工程,2011,22(23):2834-2838.

[9] BOYSEN N, BOCK S. Scheduling just-in-time part supply for mixed-model assembly lines Original Research[J]. European Journal of Operational Research,2011,211(1):15-25.

[10] FATHI M, ALVAREZ M J, MEHRABAN F H, et al. A Multiobjective Optimization Algorithm to Solve the Part Feeding Problem in Mixed-Model Assembly Lines[J]. Mathematical Problems in Engineering,2014(1):1-12.

[11] DANTZIG G B, RAMSER J H. The Truck Dispatching Problem[J]. Management Science,1959,6(1):80-91.

[12] MOSHEIOV G. The Traveling Salesman Problem with Pick-Up and Delivery[J]. 1994,79(2):299-310.

[13] GULCZYNSKI D, GOLDEN B, WASIL E. The split delivery vehicle routing problem with minimum delivery amounts[J]. Transportation Research Part E,2010,46(5):612-626.

[14] 杨仁法,龚延成.带时间窗车辆调度问题的蚁群算法[J].交通运输工程学报,2009(4):71-74.

[15] 蒋欢欢.基于精益理论的装配车间生产物流优化研究[D].杭州:浙江理工大学,2017.

[16] 韩敏,刘旭,潘振.一种动态循环取货的入厂物流策略及其线路规划研究[J].物流技术,2013,32(17):390-394.

[17] 朱玲,吴迪.需求可拆分的汽车零部件循环取货路径优化研究[J].计算机应用研究,2013,30(6):1647-1651.

[18] 李杨,赵清.汽车零部件入场物流循环取货车辆路径优化研究[J].物流工程与管理,2017,39(1):61-62.

[19] 宋志华,张晗,惠晓滨,等.导弹作战行动网络流模型及动态规划算法[J].解放军理工大学学报(自然科学版):1-5.(2017-04-14)[2017-09-24].

[20] 王梓行,姜大立,杨李,等.战时导弹火力打击任务分配与运输决策模型[J].后勤工程学院学报,2017,33(4):77-85.

ResearchonOptimizationofMulticycleLogisticsSchedulingProblemwithPickupandDeliveryinAssemblyPlant

HANShuguanga,JIYuanyuanb

(a.School of Science; b.School of Economics and Management,Zhejiang Sci-Tech University, Hangzhou 310018, China)

Starting from the perspective of lean logistics, stop for materials, finished products stock, vehicle congestion and other problems in assembly plant increase the production cost, and the serious waste of resources exists in traditional goods delivery. This paper tries to focus on the relationship between cycle feed and the cycles. Besides, multi-cycle logistics scheduling model with pickup and delivery in which time window was taken into account was established. The power tools assembly plant of S Company was taken for example. The single cycle optimization model and multicycle logistics scheduling optimization model were used to solve the problem, and the specific scheduling scheme was provided by Lingo programming. The two schemes were compared. The results show that the multicycle optimization model is much better than the single one, because it can further reduce the cost.

lean logistics; pickup and delivery; time window; multicycle

钱一鹤)

F224.9

A

1673- 3851 (2017) 06- 0497- 08

10.3969/j.issn.1673-3851.2017.12.003

2017-09-07 网络出版日期： 2017-12-01

国家自然科学基金项目(11471286，11701518)

韩曙光(1977-)，男，江苏建湖人，副教授，博士，主要从事物流与供应链管理及优化、算法设计与分析等方面的研究。