基于熵权法与灰色关联法的灌水方式优选
2017-12-26张泉
张 泉
(太原高新技术产业开发区,山西 太原 030006)
基于熵权法与灰色关联法的灌水方式优选
张 泉
(太原高新技术产业开发区,山西 太原 030006)
本文提出结合熵权法与灰色关联法的优选模型,为灌水方式的优选提供依据。首先为了避免传统方法主观设定权重的不足,使用熵权法计算指标权重,接着使用灰色关联法计算每一指标值与对应最优指标值的关联度,然后把一个方案里所有指标值的关联度按照权重组合成一个综合关联度,其中这个综合关联度表示该方案与理想方案的关联度,最后根据综合关联度进行方案优选,并把最后的决策结果与TOPSIS模型法和灰色关联投影法的优选结果进行比较。结果表明3种方法的优选结果一致。由此可见,结合熵权法与灰色关联法的优选模型适用于灌水方式的优选。
节水灌溉;熵权法;灰色关联法
1 引言
当前全国农业灌溉用水的供需矛盾十分尖锐[1],因此要加强对水资源的节约和保护。当前比较普遍的灌水方式主要有管道灌溉、喷灌、滴灌、涌泉灌等,根据每一个灌区的具体情况,从这些灌水方式中优选出一个能够最大化兼顾这一灌区的节水目标和灌溉效益的灌水方式是解决当前水资源短缺的一种有效的非工程措施。因此,有必要对灌水方式的优选方法进行研究。
当前灌水方式的优选方法主要有:层次分析法、TOPSIS模型法、灰色白化权函数法[2]、模糊综合评价法[3]等,这些方法都存在一定的不足,比如层次分析法存在主观性强的缺点、TOPSIS模型法会受到指标相互关联的影响、而模糊综合评价法会使得方案的一部分信息丢失[4]、灰色白化权函数法在白化权函数的构造上存在很大的主观性。在灌水方式的优选中,普遍存在的是不确定的灰色信息,同时加上评价指标之间的隐性关联,这些都是灰色关系。所以灰色关联法在灌水方式优选问题方面具有一定适用性。
使用结合熵权法的灰色关联法对灌水方式进行优选,并结合实例进行演算,并与TOPSIS模型法和灰色关联投影法的优选结果进行比较验证,以期为灌水方式的优选提供新思路。
2 模型介绍
2.1 熵权法计算权重
熵表示物质微观热运动时的混乱程度,所以熵值越小,说明指标的变异程度越大,故其提供的信息也越大,所以应给其赋予更大的权重[5]。具体计算步骤如下:
假设备选的方案有n个,同时每一个备选的方案又对应着m个指标,则可以构成下面的指标值矩阵。

其中,xij表示方案i的第j个指标值。
为了消除各个指标间由于物理量纲影响而引起的数量级变化,需要对指标值进行标准化,采用下式对指标值进行标准化。

其中,yij为标准化后的指标值。
使用(2)式对(1)式中的每一个指标值进行标准化转换后,可以得到以下矩阵:


最后使用下式即可以算出每一个指标的权重(wj)。
接着使用(4)式和(5)式计算熵值(ej)和信息效用值(fj),具体公式如下:

2.2 灰色关联法优选方案
关联度表示两个有序数列之间的相互关联程度[6],可以根据各个方案与理想方案的关联度进行排序,最后定出最优解。详细计算步骤如下:
首先需要定出理想方案每一个指标的指标值,可通过式(7)和式(8)求出。
当指标j是效益型指标(指标值越大方案越优的指标)时,使用下式计算理想方案的指标值。

当指标j是成本型指标(指标值越小方案越优的指标)时,使用下式计算理想方案的指标值。

从而可以得到理想方案的指标集,把理想方案的指标集与(1)相结合就可以构造出以下矩阵:
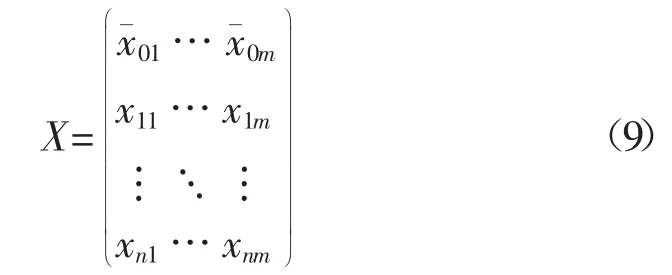
接着需要对矩阵(9)的每一个指标的指标值求其的初值像,见公式(10):

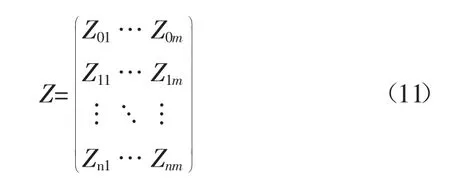
其中,zij为指标值xij的初值像。
从而可以构造初值像矩阵,见式(11):
通过式(12)求得每一个指标与理想方案对应指标的关联度。

其中,k(ij)表示指标zij与理想方案对应指标的关联度,λ一般取0.5。
接着使用式(13)求每个方案与理想方案的关联度。

最后根据“关联度越大方案越优”的原则(称为原则一)对方案进行排序,从而得出最优方案。
3 实例分析
某灌区的灌水方案有管道灌溉、喷灌、滴灌、涌泉灌4个,且各个方案的指标值见下表[7]。
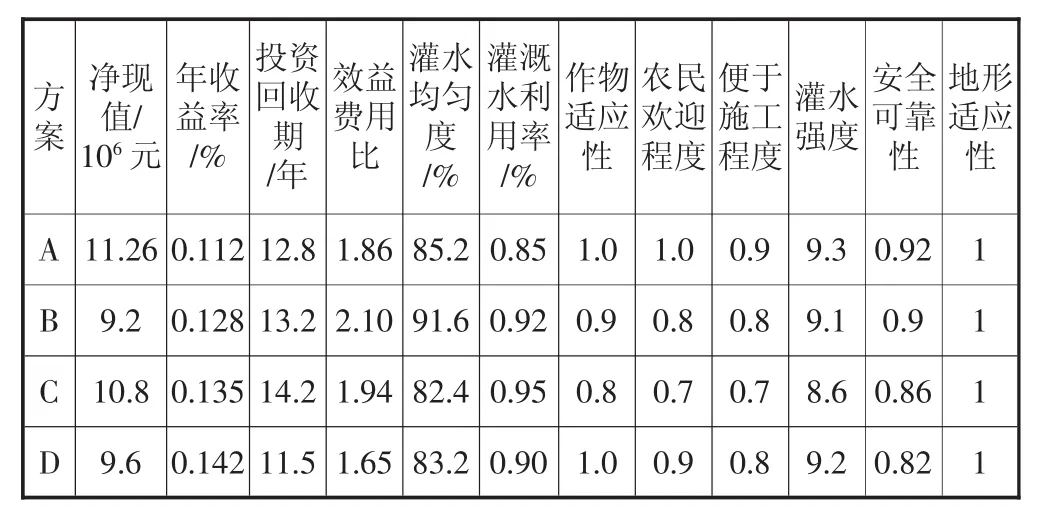
表1 各方案评价指标值
由表1可以得出矩阵(1)中n=4,m=12,然后使用式(2)进行标准化得出矩阵(3),然后使用式(4)—(6)可以计算出各个指标的权重,结果为:除了“农民欢迎程度”这一指标权重为0.084以外别的指标权重均为0.083。
然后使用式(7)、式(8)得出理想方案的指标集(只有投资回收期是成本指标,别的皆为效益指标)(11.26,0.142,11.5,2.10,91.6,95,1.0,1.0,0.9,9.3,0.92,1.0)。结合矩阵(1)就可以构造矩阵(9),见以下矩阵。

根据以上矩阵使用式(10)对每一个指标值进行初值化,然后可得以下初值像矩阵:

接着使用式(12)、式(13)计算每个方案与最优方案的关联度,见下表。

表2 各方案关联度
然后根据原则一,得出各个方案的优先顺序为:A>D>B>C。
4 成果对比
把计算得到的结果与TOPSIS模型法和灰色关联投影法的优选结果进行比较,比较结果见表3。
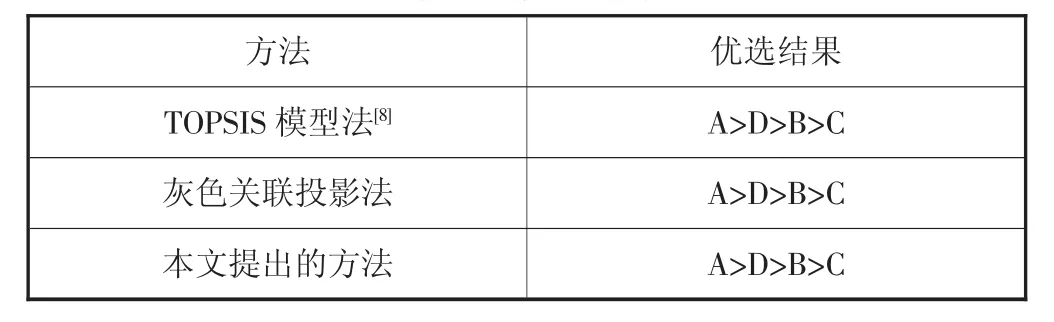
表3 各个方法优选结果对比表
5 结论
以具体灌水方式优选为基础,提出结合熵权法与灰色关联法的优选模型,且把该方法的优选结果与TOPSIS模型法和灰色关联投影法的优选结果进行比较,经比较3种方法优选结果一致,说明结合熵权法与灰色关联法的优选模型的计算结果比较可靠,优选模型对以灌水方式优选具有一定适用性。
[1]彭世彰,艾丽坤.提高灌溉水利用系数,保障国家粮食安全与水安全[J].水资源保护,2012,28(3):79-82+87.
[2]沈俊源,吴凤平.基于灰色白化权函数的农业节水灌溉项目投资决策研究[J].江西农业学报,2016,28(5):118-121.
[3]严乐军.模糊综合评判法在节水灌溉项目投资决策中的应用[J].节水灌溉,2000,(4):11-13,42.
[4]虞晓芬,傅玳.多指标综合评价方法综述[J].统计与决策,2004,(11):119-121.
[5]王健海,曾桢.多维度战略数据的Chernoff脸谱图表示方法与实证研究[J].现代图书情报技术,2010,(Z1):15-21.
[6]刘思峰,党耀国,方志耕,等.灰色系统理论及其运用[M].北京:科学出版社,2010:62-63.
[7]门宝辉.选择节水灌溉方式的灰色关联投影法[J].沈阳农业大学学报,2004,(Z1):476-479.
[8]邓丽娟,马爱玲.基于CRITIC权重与TOPSIS模型的节水灌溉方案优选[J].水科学与工程技术,2010,(2):10-12.
S275
C
1004-7042(2017)11-0042-02
张泉(1968-),女,1990年毕业于太原理工大学水文水资源专业,高级工程师。
2017-09-19;
2017-10-26
