锐角三角函数的创新题

文/刘顿

锐角三角函数的创新题

文/刘顿

锐角三角函数是初中数学的重要内容.在中考中，出现了以考查创新思维能力为目的的新题型.现归纳总结如下,供你学习时参考.

一、规律探究

例1如图1，把n个边长为1的正方形拼接成一排，求得计算tan∠BA4C=_____，…按此规律，写出tan∠BAnC=______（用含n的代数式表示）.

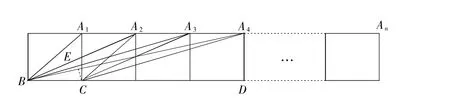
图1

解: 如图1，过点C作CE⊥A4B于E，

易得∠A4BC=∠BA4A1，

BE=4CE，而BC=1，

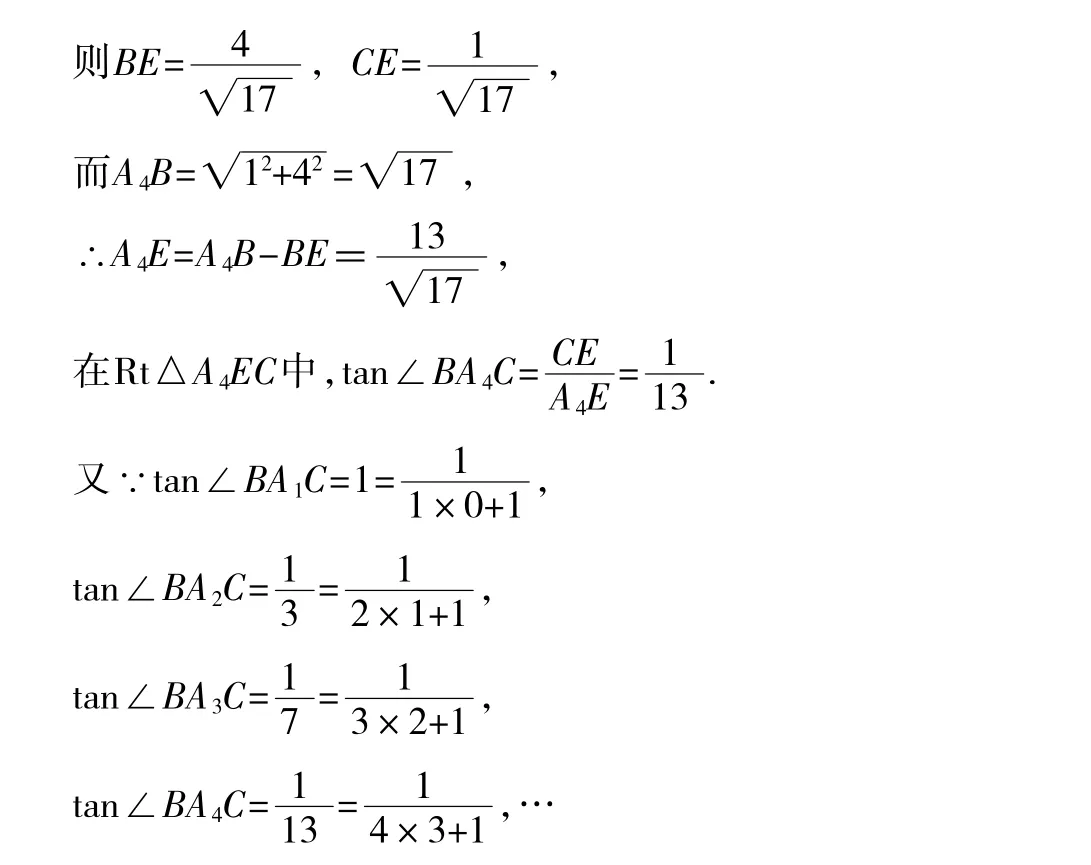
温馨小提示:在斜三角形中，需要引垂线构造出直角三角形.这道规律探究题，要通过锐角三角函数的定义，求出相应的值，从而发现规律.

二、猜想验证

例2小明在某次作业中得到如下结果：

图2

据此，小明猜想：对于任意锐角α，均有sin2α+sin2（90°-α）=1.

小明的猜想是否成立，请说出理由.

解:小明的猜想成立.证明如下：

如图2，在△ABC中，∠C=90°，设∠A=α，则∠B=90°-α，于是

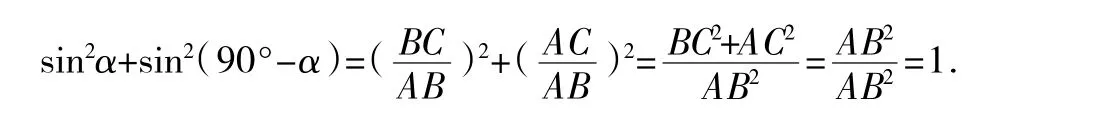
温馨小提示:理解题意并作出直角三角形，就可解决问题.

三、知识拓展

例 3 如图3，在△ABC中，设∠A，∠B，∠C的对边分别为a，b，c，过点A作AD⊥BC，垂足为D，可得

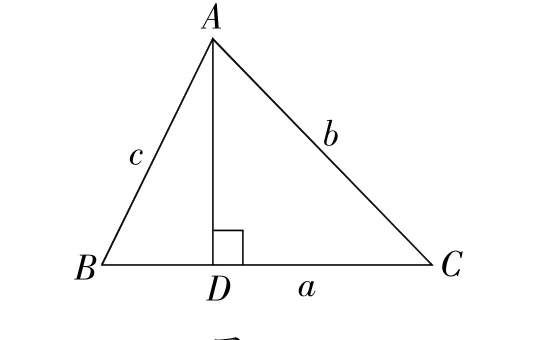
图3

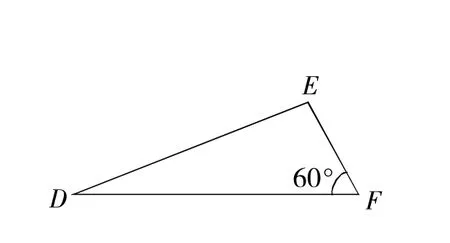
图4

通过推理还可以得到另一个表达三角形边角关系的定理——余弦定理：

在△ABC中，若∠A，∠B，∠C的对边分别为a，b，c，则

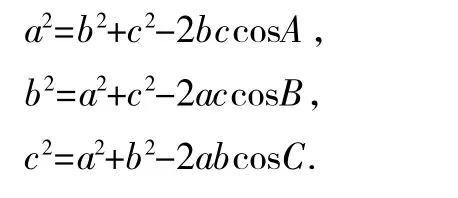
用上面的三角形的面积公式和余弦定理解决问题：

（1）如图4，在△DEF中，∠F=60°，∠D、∠E的对边分别是3和8，求S△DEF和DE2；

（2）如图5，在△ABC中，已知AC＞BC，∠C=60°，△ABC′、△BCA′、△ACB′分别是以AB、BC、AC为边的等边三角形，设△ABC、△ABC′、△BCA′、△ACB′的面积分别为S1、S2、S3、S4.

求证：S1+S2=S3+S4.

解:（1）如图4，在△DEF中，

∵∠F=60°，∠D、∠E的对边分别是3和8，

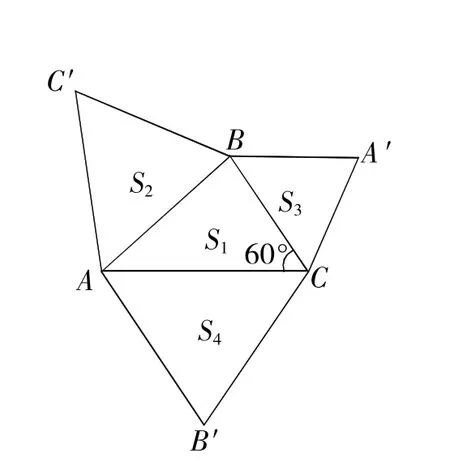
图5

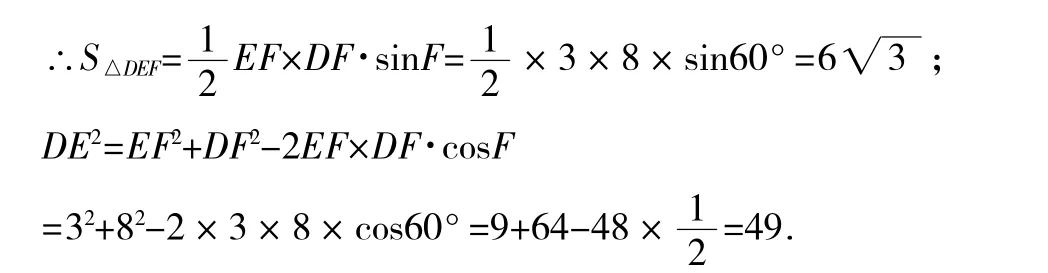
（2）证明：如图5，∵∠C＝60°，

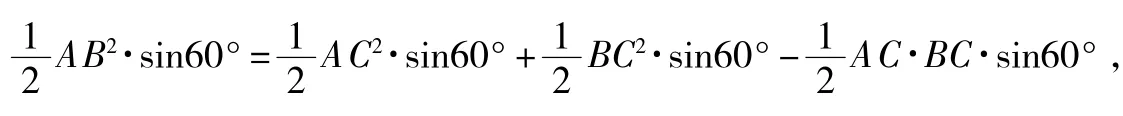
∵△ABC′、△BCA′、△ACB′都是等边三角形，

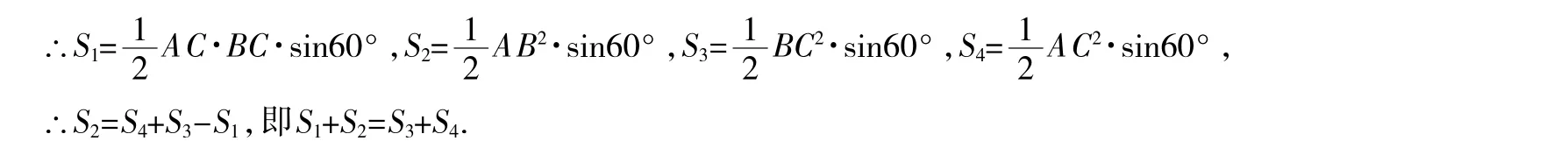
温馨小提示：要读懂题意，灵活运用条件中两类公式解题.（2）的证明还可以设∠A，∠B，∠C的对边分别为a，b，c，由三角形的面积公式，用a，b，c表示出△ABC、△ABC′、△BCA′、△ACB′的面积，即可得到S1+S2和S3+S4，最后由余弦得到a2+b2=c2+ab，从而证明结论.

王二喜