资源型城市全要素生产率及其影响因素研究

宋丽颖+刘源+张伟亮

摘要：本文运用随机前沿分析法（SFA）对2006—2014年中国109个资源型城市的全要素生产率进行测算，并运用DEAMalmquist指数法进行分解分析。发现资源型城市普遍存在全要素生产率下降的情况，而技术退步是主要原因。在此基础上，本文构建面板模型，实证检验了财政收支对资源型城市全要素生产率变动的影响。发现财政科技教育类支出所占比重、地方财政收支规模能够促进全要素生产率提升，财政分权则具有不利作用。此外，第三产业比重提升亦能有效提升资源型城市全要素生产率。

关键词：资源型城市；随机前沿模型；DEAMalmquist指数法；全要素生产率；财政收支

文献标识码：A文章编号：100228482017（06）001708

一、 引言与文献回顾

资源型城市的经济结构转型与可持续发展，始终是国内外研究的热点话题。长期依赖资源开采加工维系发展，使得资源型城市经济结构脆弱，特别是经济危机和经济二次探底以来，资源类产品价量齐跌，导致资源型城市经济增长基本停滞，部分城市实际GDP出现负增长。2015年，全国GDP增长率倒数的50个城市中，资源型城市共计31个；GDP增长率低于5%的34个城市中，资源型城市共计23个。产业结构方面，第二产业占比排名前50的城市中，资源型城市占到32个；第二产业占比超过50%的165个城市中，资源型城市占到93个。保增长、调结构成为资源型城市需要同时解决的两个核心问题。2016年中央经济工作会议指出，今年是供给侧结构性改革深化之年，要通过稳健的宏观政策、精准的产业政策以及灵活的微观政策，确保稳增长、促改革、调结构等经济工作顺利完成。而能否通过优化经济结构破除发展障碍，提升全要素生产率，寻找经济长期增长的新动力，就成为资源型城市实现转型发展的关键。

全要素生产率（TFP）旨在衡量劳动力、资本、能源等全部生产要素的产出效率，反映真实经济活动的整体效率，从而为区域经济增长、产业增长、企业发展过程中的效率贡献分析提供了依据。总结归纳可以发现，全要素生产率的理论研究主要包括三个方面，分别是基于新古典生产函数、基于超越对数生产函数以及基于前沿生产函数的研究。其中，索洛构建了基于新古典生产函数的全要素生产率理论，其核心是在希克斯中性技术进步和规模报酬不变的条件下，总产出扣除资本和劳动产出贡献后的索洛余值，即为全要素生产率。Christensen等[1]通过超越对数生产函数计算要素产出弹性和各要素的技术替代弹性，并据此反映出各投入要素的技术进步差异，并根据类似索洛余值法的计算公式得到全要素生产率。这一过程得到的全要素生产率包含了要素增进型技术进步和希克斯中性技术进步类型的生产率增长，丰富了索洛理论的内涵。

基于新古典生产函数和超越对数生产函数测出的全要素生产率只能反映出平均意义上的投入产出关系和技术水平。无法准确测算出实际产出与有效最大产出之间的全要素生产率差异，导致计算结果和理论假设存在差距。为了解决这一问题，Koopmans[2]和Farrell[3]分别定义了技术效率，前者指产出和投入达到最大边界水平时的投入产出关系，或者则是技术与价格给定条件下生产一定量产品的最小成本与实际成本之比。据此，Farrell提出了前沿生产函数，即固定投入要素所能达到的最优产出，经济行为的综合效率可以通过实际产出与最优产出之间的差距来反映。Aigner et al.[4]、Banker et al.[5]分别构建了SFA模型和BCC模型，将综合效率分解为技术效率和规模效率，如果在函数中添加时间趋势变量，还可以实现技术进步的测算。1994年，Fre et al.[6]运用Malmquist生产率指数，在DEA研究框架内将全要素生产率动态分解为技术进步率、技术效率和规模效率，进一步明确了全要素生产率包含的技术进步和制度效率。由于参数型前沿生产函数法（SFA）和非参数数据包络前沿生产函数法（DEA）不需要希克斯中性和市场出清的假定，测算结果更接近全要素生产率的实际情况，因此在实际研究中得到更为广泛的使用。最新的研究主要包括王艺明等[7]、何剑和孙鲁云[8]、冯云廷等[9]、刘承智等[10]分别对全国、各省区、特定类型城市全要素生产率的测算分析，以及李萌和杨扬[11]、戴碧艳等[12]、祝福云和闫鑫[13]、邱爱莲等[14]对战略性新兴产业、葡萄產业、轻工业、制造业等行业全要素生产率的测算分析。

城市全要素生产率影响因素的既有研究中，武彦民、杨峥[15]考察了建成区面积、城镇就业人数、能源消费量和基础设施密度对城市全要素生产率的影响，发现能源消费能够提升全要素生产率，其他因素均不利于全要素生产率提升。姚震寰、纪明辉[16]发现产业结构单一，特别是第三产业比重低于全国平均水平，是制约东北地区全要素生产率提升的主要原因。刘建国、刘宇[17]发现服务业水平、第三产业比重、经济增长、对外开放程度、基础设施水平均对杭州城市旅游全要素生产率具有正向影响。程中华、张立柱[18]考察了产业集聚对城市全要素生产率的影响，发现制造业集聚不利于全要素生产率的提升，但是生产性服务业聚集能够提高全要素生产率。董旭、吴传清[19]考察了25个主要城市全要素生产率影响因素，发现信息基础设施、人力资本、制造业集聚、经济密度和对外开放都能够显著提升全要素生产率总体水平，政府干预则具有较强的阻碍作用。

可以发现，既有关于城市全要素生产率影响因素的相关研究，多从经济增长、产业结构、对外开放等内生角度出发，鲜有关于财政等外生因素的研究。而财政因素决定了地方政府是否拥有充足财力进行产业转型，也能充分考察地方政府是否存在“财源依赖”的现象，因此，进行财政分权对城市全要素生产率影响的研究具有现实意义。本文综合两种全要素生产率测算方法的优势，运用前沿生产函数法（SFA）对109个资源型城市2006至2014年全要素生产率进行测算，同时运用DEAMalmquist方法对全要素生产率进行分解分析。在此基础上，从财政规模、财政支出结构、财政自主度等因素入手，分析财政因素对全要素生产率的影响，最后，结合资源型城市转型发展的目标和路径，提出促进资源型城市供给侧结构性改革的财政政策建议。二、 随机前沿分析模型（SFA）与endprint

DEAMalmquist指数模型（一）随机前沿分析模型（Stochastic Frontier Analysis，SFA）

本文参考刘秉镰（2010）构建的随机前沿模型假定国民经济生产函数，表示为：

lnYit=a0+a1lnKit+a2lnLit+a3t+（vit-uit）（1）

uit={uiexp[δ（t-T）]}～iidN*（μ，δ2ii）（2）

其中，i为资源型城市，t为样本年份，T为样本的基期年度，Y、K、L分别表示国内生产总值GDP、物质资本存量和从业人员数，a0～a3为待估计的未知参数；vi为随机干扰项，包括测量误差等各种不可控制的随机因素，服从正态分布；μ为非截断正态分布条件下的期望值；δ为技术效率水平随时间变动而变化的未知参数，ui为技术无效率项，服从零点截断的半正态分布。

因此，各资源型城市各年份全要素生产率为：

TFPit=exp（a0+a3t）×TEit（3）

其中，exp（a0+a3t）为t时期的前沿面技术水平，TEit为i市t时期的技术效率。

（二）DEAMalmquist指数模型

Malmquist指数最早作为消费指数使用，随后由Caves等人应用在企业生产率分析中。Fre等人进一步运用两期Malmquist指数的几何平均值定义全要素生产率增长[10]。本文运用基于DEA模型的Malmquist指数方法，分析中国资源型城市全要素生产率的动态变化特征。Malmquist生产率指数具体形式如下：

Mi，t+1=Dti（xt+1i，yt+1i）Dti（xti，yti）×Dt+1i（xt+1i，yt+1iDt+1i（xti，yti）12（4）

其中，xti、yti分别表示第i个县区在t时期的投入向量、产出向量；xt+1i、yt+1i分别代表第i个地区在t+1时期的投入向量与产出向量。而Dti（xti，yti）与Dti（xt+1i，yt+1i）分别表示在以t时期的技术水平下，t时期和t+1时期的生产点的距离函数。

分离技术进步变化和技术效率变化，得到下式：

Mi，t+1=Dti（xt+1i，yt+1i）Dti（xti，yti）×Dti（xti，yti）Dt+1i（xti，yti）×

Dti（xt+1i，yt+1i）Dt+1i（xt+1i，yt+1i）12（5）

其中第一项表示t时期到t+1时期生产效率的变化，第二项表示技术的变化率。

Mi，t+1=Dtv（xt+1i，yt+1i）Dtv（xti，yti）×Dtv（xti，yti）Dtc（xti，yti）

Dt+1v（xt+1i，yt+1i）Dt+1c（xt+1i，yt+1i）×Dtc（xti，yti）Dt+1c（xti，yti）Dtc（xt+1i，yt+1i）Dt+1c（xt+1i，yt+1i）（6）

（6）式的变化放松了（4）、（5）两式关于规模报酬不变的假设。其中c、v表示规模报酬不变和规模报酬可变的情况。通过这一计算式将效率变动分解为纯技术效率变动和规模效率变动，其中第一项表示变动规模下的纯技术效率变化（pech），反映技术运用水平带来的效率变动；第二项表示规模效率变化（sech），反映决策单元是否在最佳规模下运营；第三项表示技术进步率（techch），其值大于1表示存在技术进步，小于1表示存在技术退步。三、 数据说明与测算结果分析

（一）实证数据说明

本文以资源型城市为研究对象。根据国务院2013年颁布的《全国资源型城市可持续发展规划（2013—2020）》，全国共有262个资源型城市，包括126个地级行政区、62个县级市、58个县以及16个市辖区。考虑数据可得性原则和同行政层级原则，本文最终选取109个地级行政区（包括地级市、地区、州）为研究样本。其中成长型城市12个、成熟型城市60个、衰退型城市22个、再生型城市15个。样本虽然没有覆盖全部的可研究城市，但是已经具有足够性。研究时间段选取为2006年至2014年，该时间段包括了中国经济的高速增长阶段（2006—2007年）、受經济危机影响的快速探底阶段（2008—2009年）、四万亿财政政策的短期反弹阶段（2010—2012年）、结构性矛盾导致的二次探底阶段（2013—2014年），由于资源型城市的发展支柱是资源工业，而资源工业的发展又依赖于国内宏观经济的发展情况。因此，这一时间段的选择更能全面的反映资源型城市全要素生产率在不同经济发展阶段的变化情况，从而评估城市发展对资源工业的依赖情况。

指标选取方面，产出指标为各资源型地级市当年实际国内生产总值。因为本文的研究起点为2006年，因此以2006年为基年，将各地市各年度GDP换算为实际GDP。考虑经济波动年份不同城市的GDP平减指数差异较大，同时兼顾数据可得性原则，统计年鉴中反映城市GDP平减指数的选用该城市的平减指数，缺乏平减指数的城市则选用其所在省份的GDP平减指数。投入指标包括劳动力和资本存量指标。劳动力指标方面，本文选择全社会从业人员数。资本指标为当年物质资本存量，由于我国没有物质资本存量的具体统计数据。本文以单豪杰[20]测算的2006年全国物质资本存量为基准。由于缺乏各地市物质资本存量的统计数据和测算数据。本文参考既有研究的处理方法，根据各资源型城市当年GDP占全国当年GDP的比重，同比例分配当年全国物质资本存量至各地市，从而估算各地市2006年物质资本存量。在此基础上，运用永续盘存法，以2006年价格为基准，计算各地市每年资本存量，计算公式为：

Ki，t=Ki，t-1（1-δi，t）+Ii，t（7）

其中，Ii，t为第t年i地市的固定资产投资总额。由于无法完全获得所有地级市每年固定资产投资价格指数，缺乏固定资产投资价格指数的地市，根据各年份各城市所在省份固定资产投资价格指数进行调整，进而换算成以2006年为基准的实际固定资产投资总额。endprint

δi，t为存量资本折旧率。本文选用单豪杰测算结果中1997—2006年各年资本折旧率均值，即1052%，根据（7）式计算各年各资源型城市资本存量。

（二）资源型城市全要素生产率实证测算结果

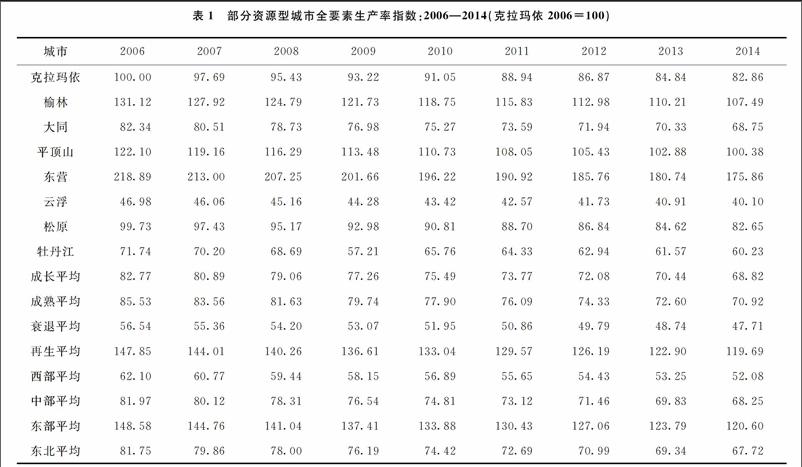
根据本文选取的109个资源型城市的样本数据，利用Frontier41软件估计（3）式，得出各资源型城市TFP绝对数值。为了便于考察各城市TFP的变化情况，令2006年克拉玛依市的TFP指数为100，定义第t年i城市的TFP指数为：

测算结果表明，109个资源型城市全要素生产率均出现逐年下降的情况。同时，各资源型城市的全要素生产率差异显著。根据资源型城市成长、成熟、衰退、再生分类可以发现，再生型城市TFP远高于其他类型城市，衰退型城市TFP指数最低。这是因为再生型城市具有更多的经济增长动力，而衰退型城市相对缺乏新的经济增长点，因此还需要继续承受资源依赖带来的负面影响。根据东、中、西、东北四大区域测算资源型城市TFP指数均值可以发现，东部地区资源型城市全要素生产率远高于其他地区，中部地区和东北地区接近，但是差距微弱扩大，西部地区垫底。这是由于东部地区具有制造业、第三产业的聚集优势，资源型城市对于资源经济的依赖程度弱于其他地区，存在其他发展动力。同时，东部地区的开放程度相对较高，加之经济实力较强、财政科技投入较大，经济转型步伐相对较快。因此，东部地区资源型城市始终保持较高的全要素生产率水平。而其他地区，特别是西部地区资源型城市普遍缺乏资源经济以外的经济支柱，经济基础薄弱、科教水平落后又决定了转型所需要的财政资金、人力物力匮乏，因此全要素生产率远低于东部地区。

（三）DEAMalmquist指数估计结果

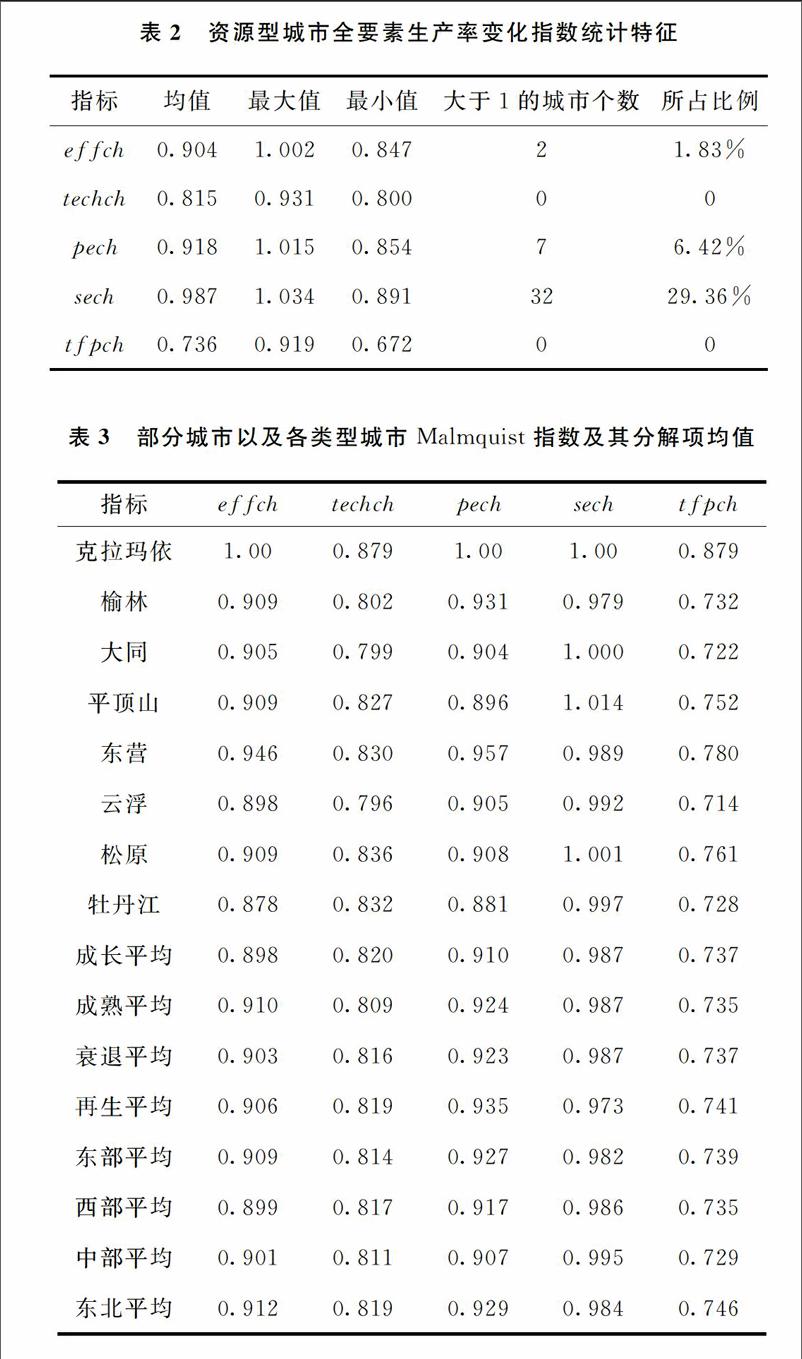
为了继续研究资源型城市TFP出现下降的原因，分析全要素生产率下降的内在动因，本文利用DEAP21软件对资源型城市全要素生产率进行Malmquist指数分解。其中tfpch代表全要素生产率变化指数（Malmquist指数），effch表示技術效率变化指数，techch表示技术进步率变化指数，pech表示纯技术效率变化指数，sech表示规模效率变化指数。对比投入导向和产出导向，发现其测算结果基本相同。为方便分析，本文后续呈现的测算结果以及全要素生产率影响因素分析均选择产出导向。

需要特别说明的是，全要素生产率分解结果中，所有城市均出现技术退步的情况。这和许多传统的研究结论相悖，与匡远凤和彭代彦[21]、屈小娥和席瑶[22]的研究结论一致。长期以来，关于技术进步率，存在“过去掌握的技术不会遗忘”的假定。根据这一假定，现实中不会出现技术倒退的现象。在企业层面的实证中，这样的假定存在较强的合理性。因为企业的投入过程中往往不会出现资本的“过度深化”情形。但是在资源型城市发展的过程中，特别是经济危机后的几年里，资源工业的固定资产投资成为了重要的经济增长驱动，加之资源工业自身又是资本密集型产业，四万亿的财政政策及其扩张效应使得资源型城市的产出资本比迅速下降。109个资源型城市2006—2014年期间全部出现了产出资本比下降的情况，产出资本比均值从2006年的2135下降至2014年的0139。但是根据DEA的分析思想，技术进步是最佳实践面是否外移决定的，最佳实践面则通过DMU中最佳实践者的投入产出数据所计算得到。只有产出投入比增大的情况下，才会出现技术进步的情况，反之则是技术倒退[21]。因此，当资源型城市产出资本比不断下降时，技术内陷的情形也就不可避免。而这一结论也比较符合资源型城市近年的发展情况。

四、 资源型城市全要素生产率变动

的财政收支因素分析（一）全要素生产率变动的财政收支因素分析模型

资源型城市转型发展恰逢供给侧结构性改革的全面深化。劳动力、资本等生产要素的深化以及在不同产业之间的优化再分配过程，需要宏观政策，特别是财政政策的引导。合理的财政收支政策，可以有效保障地方经济转型过程中的公共支出，支出规模的稳步扩大能够有效推动全要素生产率的增长和技术进步[23]。同时，财政在教育、科技等方面的领域的支出可以有效帮助资源型城市积累人力资本和技术资本。而财政补贴的结构性调整能够有效引导社会资金的优化投入，加快要素在产业间的优化分配，提高企业的全要素生产率，从而促进产业结构的升级调整[24]。因此，本文从财政收支出发，考察财政分权、财政规模、支出结构对全要素生产率和技术效率的影响，辅以产业结构变动共同分析。面板回归模型如下：

lntfpi，t=β0+β1t&ei，t+β2fisautoi，t+

β3lnincomei.t+β4lnexpenditurei，t+β5indusi，t+εi，t（9）

lntei，t=η0+η1t&ei，t+η2fisautoi，t+

η3lnincomei.t+η4lnexpenditurei，t+η5indusi，t+εi，t（10）

其中，基于SFA方法测算得到的资源型城市全要素生产率（TFP）和技术效率（TE）是被解释变量，解释变量指标含义如表4所示。其中财政自主度反映财政分权情况，科教投入程度反映财政支出的结构性偏好，人均财政收入和支出反映财力状况。对于人均财政收入与人均财政支出采用对数化处理。表4全要素生产率及技术效率的解释指标说明变量名称变量符号变量说明科教投入程度t&e财政科技教育支出占地方财政支出比重财政自主度fisauto地方财政收入占地方财政支出比重人均财政收入income人均地方财政收入人均财政支出expenditure人均地方财政支出产业结构indus第三产业比重

（二）面板模型回归结果

从回归结果来看，财政科技教育支出占比、人均财政收入、人均财政支出以及第三产业占比提升均对全要素生产率、技术进步率以及技术效率的提升具有促进作用。财政自主度的提高对全要素生产率、技术进步率和技术效率具有阻碍作用。endprint

首先，全要素生产率的提升，其本质是人力资本水平和科技水平的提升。因此，财政支出中科教支出比重的提升对于全要素生产率提升意义重大，另一方面也说明，从提升全要素生产率角度出发，资源型城市财政科教支出是有效率的，但是从系数值来看，科教支出占比提升1%，全要素生产率提升0554%，技术效率提升0685%，说明对于财政科教支出的使用效率仍有较大的提升空间。此外，从统计结果看，资源型城市财政科技教育支出普遍偏低。2014年，我国公共财政科教支出占公共财政支出的比例为1868%，在资源型城市中，有58个城市科教支出占比低于上述值，其中牡丹江等6座城市的比例值低于10%。由此可见，资源型城市在稳步扩大财政科教支出规模的同时，也应当提升财政资金使用效率。

财力方面，人均财政收入每增加1%，全要素生产率提升0231%，技术效率提升0336%；人均地方财政支出每增加1%，全要素生产率提升1128%，技术效率提升1242%。说明资源型城市财力提升对全要素生产率提升十分关键。2014年，93个资源型城市人均财政收入低于全国平均值，96个城市人均财政支出低于全国平均值。资源型城市普遍存在财力不足的问题。由于发展模式的特殊性，我国资源型城市发展重心长期在工厂建设方面，特别是政企不分地区，在企业代行政府职能的年份，往往忽略公共设施建设和修缮。导致资源型城市基础设施条件普遍落后。滞后的公共服务和社会保障严重制约了人力资本的发展。而要弥补上述不足，资源型城市必须拥有充足的财力。因此，在转型过程中如何开辟新财源，保障地方政府拥有充足财力解决历史遗留问题，迅速弥补社会保障和公共服务领域的短板，就成为了资源型城市能否实现转型目标，实现全要素生产率提升的关键。

从财政自主度的系数来看，地方财政自主度越高，全要素生产率、技术进步率以及技术效率反而下降。也就是说，地方财力和地方财权对全要素生产率以及技术进步率的影响是背道而驰的。说明现行的财政分权体制并不利于资源型城市转型发展。如上文所述，科技、教育、社会保障等公共服务水平的提升是全要素生產率和技术进步率提升的关键。然而，无论是本文的研究，还是大量前人研究都表明，在中国式财政分权下，地方政府更倾向于在“短平快”的基础设施领域进行投资，而科学技术和人力资本领域的投入难以在短期内转化为经济增量，因此为了刺激经济增长，资源型城市新增财力更多地投入到容易刺激需求的相关领域。进一步缩减民生类公共服务领域投资。

从实证结果来看，第三产业比重的提升确实对全要素生产率和技术进步率起到正向促进作用。第三产业比重每提升1%，全要素生产率提升0849%，技术效率提升0874%。第三产业多为人力资本密集型和技术密集型产业，可以吸纳更多优质人力资本和先进技术投入城市发展。同时第三产业中的交通运输、仓储和信息传输等行业可以有效降低其他产业的运行成本，从而提高经济运行效率。需要注意的是，第三产业比重提升1%，资源型城市全要素生产率和技术进步率提升低于1%，说明第三产业自身的结构存在进一步优化的空间。如何优化第三产业结构，避免因为追求产业规模而导致“产业低端化”，对于提升城市全要素生产率和技术进步率也十分关键。五、 结论与政策建议

资源型城市的转型发展的最终目标，是提升全要素生产率。本文研究结果表明，2006年至2014年间，我国资源型城市普遍出现全要素生产率逐年下降的情况。同时，全要素生产率呈现明显的区域差异和城市类型差异。东部地区和再生型城市全要素生产率显著高于其他地区和其他类型城市。对全要素生产率进行分解后可以看出，技术退步是导致全要素生产率逐年下降的主要原因，成熟型城市和中部地区的技术退步情况最为严重。

资源型城市的转型发展过程中，需要财政政策的有力支持。本文研究结果表明，提高财政科技支出占比、提升城市财政收支规模对于提升城市全要素生产率十分关键。因此，应当以不低于全国平均水平为最低标准，稳步提升资源型城市财政科技教育支出比重，同时辅以个人所得税科教支出税前抵扣政策，从公共支出和家庭支出两方面提升科技教育总支出。实证结果同时表明，资源型城市财政科教支出的使用效率仍存在较大的提升空间。但是，以财政自主度度量的财政分权并不利于全要素生产率的提升，考虑中国式财政分权下地方政府GDP为导向的支出偏好，在下一阶段应当加大上级政府转移支付在财力中的比重，控制资源型城市的财权。

产业结构的优化升级对于全要素生产率提升十分关键。本文的研究结果表明，第三产业比重的提升能够有效提升资源型城市全要素生产率，但是这一促进作用仍然存在较大的提升空间。因此，应当通过税收优惠和财政补贴等财税政策，积极引导资源型城市产业结构升级。一方面是根据自身区位优势和发展特点提高第三产业相关行业的比重；另一方面优化第三产业内部的结构，第三产业内部技术密集型和劳动密集型产业共存，提高技术密集型产业的比重，通过研发费用加计扣除等手段积极鼓励高新技术产业进行技术创新，避免第三产业低端化。同时， 加快资源工业等第二产业自身产能整合， 淘汰落后产能、整合规模不足产能、转化有条件产能。不断延伸资源开采和加工产业链， 例如传统煤炭开采业过剩产能向煤制油、煤制烯烃、煤制天然气等领域的转型。同时， 通过所得税减免、税前加计扣除、增值税即征即退等税收优惠和财政补贴政策， 鼓励传统资源行业技术研发、固定资产升级和产品结构优化， 加快产业转型， 使资源工业再次成为资源型城市发展的强力引擎。参考文献：

[1]Christensen L R， Jorgenson D W， Lau L J. Transcendental logarithmic production frontiers [J]. Review of Economics and Statistics， 1973， 1（55）： 2845.

[2]Koopmans T C. Activity analysis of production and allcation [M]. New York： Wiley， 1951.endprint