非线性思维观下的图案设计及应用

唐 颖,陈楚婷

(江南大学 纺织服装学院,无锡 江苏214122)

非线性思维观下的图案设计及应用

唐 颖,陈楚婷

(江南大学 纺织服装学院,无锡 江苏214122)

通过分析非线性思维及非线性图形的定义和特点,提出了基于非线性思维的图案设计方法,并延伸至实际设计及应用;同时结合非线性思维理论及原理探讨了在实际设计过程中发现的问题和应用成果。

非线性思维;分形理论;图案设计

1 非线性思维观

1.1 非线性思维的定义

非线性是当今科学界的前沿与热点,涉及自然科学、人文社会科学和哲学等众多领域。它在20世纪60年代兴起,虽其概念、性质至今仍在发掘之中,但无疑已经影响了人们的思维方式,改变了人们对世界的认识,在当今众多前沿学科的研究中发挥了重要的作用[1]。非线性思维方式在艺术设计领域也逐渐渗透进来,尤其在建筑设计、景观设计等方面已经出现了一些实践非线性思维的设计案例[2-3]。非线性思维中时空观念的转变,以及对自然界复杂事物自组织规律、审美原理的揭示,为艺术设计的现代发展注入了新的空气。非线性思维广义来说就是与常规的线性思维不一样的思维方式,看问题的逻辑与角度相对于线性思维而言没有那么多惯性和常理。非线性思维是一种相互作用、无限制、无边界、非单一立体化或平面化的交织结构,类似于植物的根茎与叶脉。而线性思维可能只是单一的、同一维度的、不多变的。

在非线性思维系统中,变化及变量是不可估摸的,它很有可能因为当中的某一个微小的因素改变整个形势的现状,而无从知晓形势发生变化的源头。相对于许多线性思维看问题时需要通过大量以往的经验和信息的分析形成的惯性思维,具有很大的局限性和不可变性的。非线性思维的未知性较强,所呈现相关的内容的拓展性和可变性也更强。用非线性思维的角度看问题能更全面更深入地了解问题的本质,也能使人们更加客观地去看待许多问题。非线性思维实际上包含了线性思维,非线性思维无处不在,但大多数情况下人们由于思维局限、思维惯性而将其以线性思维去理解和感受,从而使非线性思维这一概念,在艺术设计领域还是比较陌生。

1.2 非线性图案的定义

非线性图案是运用非线性理论或非线性思维方式产生的图形,非线性图案并不单一由直线或者曲线构成,也不需要通过线条的组合及排列而形成千变万化的图案,可理解为一种多维状态的图形,这一点与线性图形是有所区别的。同时,它还具有一定的数学特性和物理特性,也可通过数据运算、函数公式输出等,加入计算机编程语言软件的辅助或将数据直接输入特定的软件当中,所输入的内容将以图形的形式呈现在荧幕上。

2 非线性思维设计方法

在展开设计之前,将设计思路分为几点:一是目前关于非线性思维的图案其实并不多见,希望在传统的图案设计方向上,加入非线性的思维,从而发掘并总结出一些非线性图案的特征及特点;二是从收集的图案资料中截取部分元素对其进行设计,其难点关键在于设计过程如何保持非线性图案的特点,同时又具有独特的审美风格;三是对于现有的图案形式通过解构、重组、倒序等手段加以创新。

2.1 突破性——打破传统与形式美法则的新式设计理念

从以往对于图案设计的经验来看,大多数设计师的灵感来源于线性思维,对于美好的事物潜意识中将其具象化或线象化,常采用勾线法和色彩平涂法进行图案设计并且十分注重图案的连续性和完整性。而非线性思维观希望能打破这一传统的设计惯性,通过不同的表现手法、立体团内部空间的扭曲等等营造图案从固定形态到动态美感这一审美形式的转变。其实在非线性理论中存在很多现象,如混沌、频率与振幅的关系、分谐波振荡、多值响应等。换而言之,在线性理论中是很难得到这些奇怪的现象,比如在线性函数中,当X轴数值发生改变,随之Y轴必定会随之变化,这种变化是单一的、同一平面内的;而若在非线性函数中,将一个数值带入其中可能会使得整个函数现象发生多种形式的变动,而这种变动是多向的,甚至有可能延伸至整个空间,产生多维度的变化。正是种种的不确定因素造就了非线性的“标新立异”,这种“标新立异”也是非线性思维奇妙之处。对比传统图案设计,是需要以“标新立异”的思维进行创新和设计的,若能将非线性思维融入到设计中,就算基础图案是一条简单的直线或者四方形,在非线性思维中它是有无限种可能性的,可对简单图形组织、变换,形成新的图形,甚至形成立体图案。

同时,在传统的图案设计中形式美法被十分看重,希望通过图形直接的冲撞重叠,打破平衡感,营造出“不完整”的视错效果,使得图案在视觉效果上得到新的开发。

2.2 自相似性——从生活中寻找灵感再归于生活

自相似性这一特点最初是在非线性思维中一个分支——分形理论中发现的。分形的概念最初是由美国著名数学家本华·曼德博提出的,在他1967年发表的著名论文《英国的海岸线有多长?统计自相似和分数维度》中提到:英国的海岸线长度是无法确定的,在测量过程中它存在的变量太多,而单纯依赖于测量的尺度是无法将其精准测量出来的。简单来说,由于大大小小的岛屿及海峡轮廓有着数以万计的变化,所以在可视范围内,我们无法很清楚地将其局部形态和整体形态很好地区分完整,但它们之间是具有自相似性的。而类似这种整体与局部之间具有一定的相似性但又有所区别,可以理解为分形[4]。实际上,分形理论就是非线性理论的一个分支,它的自相似性、不完整性等都与非线性理论中的概念十分接近。浅显一点来理解,它与相似有一定字面上的相同,而在实际中是不一样的,所谓自相似性,是图像与图像直接具有相似之处,无论整体图像是如何变化,其内部图像之间总是保持着一定的自相似性。但自相似性又不能简单地理解为某一个图像和某一个图像一样,它们只是处于一个相似的状态下,同时具有自己的特征[5]。生活中随处可见分形的踪影,如铁锈、干裂的土地、叶片、扎染图案、刺绣等,可见分形是一种非常贴近人们生活的概念,而图案设计本身也是服务于生活,因此更应该注重对其的理解和运用。

2.3 整体性——运用非线性思维把握整体与局部的关系

整体性的简单概念是图案无论从整体上看还是局部上看,它都是具有美感的,尽管遵循不完整原则,但一定要把握住整体与局部的关系。参考现有的部分非线性图案设计,发现容易出现的问题是在局部过于繁杂导致形成整体图案时便显得累赘。在非线性的概念中,其中的变量会引起无穷大的变化,但这种变量是关系到整个图像的,简单来说就是它小的变量形成的影响是一整个部分的而不是单一存在的。无论是服装设计还是家纺设计,都会注重作品的系列感,所谓的系列感即整体视觉上的感受,所以整体性在此就显得尤为重要了。而当前图案设计中的系列普遍来说都是简单的复制、组合,并没有过多的组织或者完善,在设计图稿的过程中,能做到的就是将设计的思路连成一个整体,设计的风格、种类可以是多样化的,但每一个系列设计中必须注重的就是整体性。不仅考虑到结果,还要注重过程,这是非线性蕴含的又一思维方式,根据这一点也有助形成系列化图案。

同时,为了使得图案不局限于某类服饰或纺织品的应用,尝试在应用中尽量拓展图案的使用率,而为了能扩大使用范围,在设计图案时就要考虑到图案的可延伸性,所设计的图案必然是具有一定可塑性和可转换性的,这也是非线性整体思维的体现。

3 非线性思维设计实例分析

在设计的过程中,想法和创意是最重要,经过对非线性的分析及设计思路的整理,总结了非线性图案具有其自身特性[6]。如不完整、破碎、无限性、自相似性等,这些特性的发现为之后的设计提供了很大的帮助,将这些特有的性质相互交织,融会贯通,最终成功实现一系列的设计方案。

3.1 病原体系列

病原体系列图案设计的灵感源泉是基于分形理论,但并不同于一般数理运算形成的分形图案。许多非线性函数中,分形本身就是一种会随着数据变动而产生不同节奏和韵律的无规则、无限定的图形。在传统的图案设计中,十分注重图案之间的构成感,比如形式美法则中的对称、统一、对比等,很多时候都成为人们评判一幅设计作品好坏的准则。病原体是细菌、病毒、寄生虫、真菌等可造成生物感染疾病的微生物的统称。大多数病原体在一定条件下是会自我进行培养和繁殖的,而在繁殖过程中不断地分裂、破碎、结合成新的病原体。这一生物特性和分形几何及混沌力学中提到的打破、重构等概念十分类似,而在设计成果(图1)中可以发现,绘制图案时并没有单独将某一种元素过多地重复或相互对应,而是从整体上所有的内容都是相映得彰,环环相扣的,这是对于传统图案设计概念的一种打破和冲击,同时又成功将分形图案的自相似性,局部与整体相呼应的特性表现出来。在图案的细节处理上,放弃了传统图案的讲究和严谨,将细菌、真菌等复杂难以表达的元素简单化,再通过彼此之间的联系以及巧妙的布局,使得设计稿在不经意间被完整,富有独特的韵律和张力。

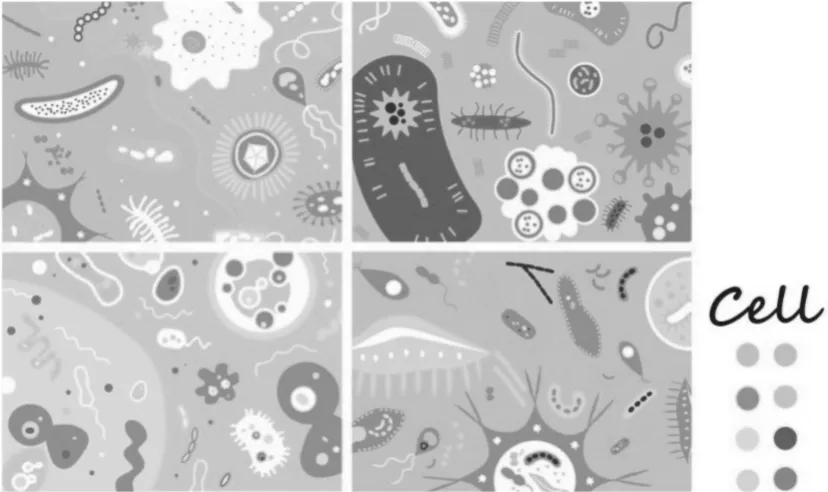
图1 病原体系列图案设计

3.2 万花筒系列

万花筒作为一种利用物理光反射原理的玩具,将不同形态的实物放于圆筒底部,通过窥孔即可看到其形成的特殊镜像图形。这种对称图形会随着圆筒的转动而源源不断地形成许多有趣的图像,是抽象而又千变万化的,具有非线性图案的特征。这种图像的形成并不由单一的点、线、面组成,而是互相交替产生的,所以若单独将成像结果截取出来,人们很难根据成像猜到原始物体的全部,这给予人们很大的空间去想象,拓展了人们的思维,产生了趣味之处。

在设计该系列的初始阶段使用了手机软件对物体做万花筒效果处理,发现简单地将物体以万花筒的形式展现并不能使用且形成的图像十分粗糙。但大量的拍摄工作和图像截取为设计提供了灵感及元素,因此从中选取部分的图像用绘图软件将设计元素规整化,从而形成图案,如图2所示。与其他系列的区别在于万花筒系列图案中遵循了万花筒与传统图案共有的特性——四方连续性。其原因在于使得图案能被更广泛地运用在不同的产品当中;且在于由于万花筒特性所致,形成的图案容易繁杂花哨,四方连续的形式可使保证在不失去图案原本随意性的情况下保持图案完整性,即趋于整体又不失局部,体现了非线性思维中整体与局部之间的关系。

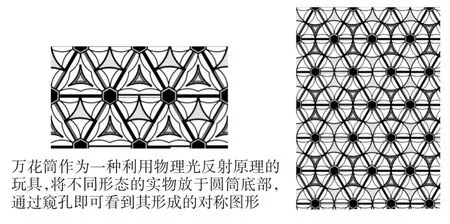
图2 万花筒系列图案设计

4 设计图案应用实例

在设计应用时,选择将细菌系列图案作品与女童装相结合(图3)。在童装日常服饰设计中,衣服易穿脱性十分重要,这是为儿童在没有成年人辅助的情况下也能自行穿脱为出发点作为考虑,因此款式设计上我们没有运用太复杂的服装结构,主要以基本款为主:连帽卫衣、蓬蓬裙、针织外套、背带裤、T恤以及连衣裙等。也正因为款式较为简单,因此我们选择了色彩较丰富且具有趣味性的病原体系列图案,这样不仅能让款式看上去没有那么普通,而且趣味性的图案能使人产生愉悦的心情,并且符合孩童活力青春的可爱形象,比市场上常见的卡通形象或日常的印花图案更能打动消费者。

图3 病原体系列图案在女童服装设计中的应用

5 结语

自然界的非线性特征中隐藏着十分庞大的灵感源泉,不是通过简单的概念性分析和设 计就能将其把握的。图案设计案例所使用的设计灵感元素的病原体、万花筒等都是生活中十分常见而不起眼的“小东西”,但往往这样不起眼的“小东西”却蕴含了很丰富的变化和独特的美感。如何用非线性这一思维去看待问题,在有限的范围内对生活进行无限的思考,就如同非线性思维一样具有无穷的探索空间,从而能够创造出更多美好的事物。

[1] 李润珍,武 杰.非线性提供了一种新的思维方式[J].科学技术与辩证法,2003,20(2).26-29.

[2] 龚晓文.非线性思维及其在建筑中的应用研究[D].长沙:湖南大学,2008.

[3] 匡 纬.基于非线性思维观的景观设计策略研究[D].北京:北京林业大学,2011.

[4] 桑莉君.现代设计中的分形艺术研究[D].太原:太原理工大学,2015.

[5] 代沛涵.分形图案在纺织纹样设计上的应用[D].苏州:苏州大学,2015.

[6] 唐 颖,房宽峻,沈 雷.分形图案与传统纺织印花图案的形式美感对比[J].纺织学报,2009,30(12):90-94.

Pattern Design and Application under the View of Nonlinear Thinking

TANG Ying,CHEN Chu-ting
(School of Textiles and Clothing,Jiangnan University,Wuxi 214122,China)

Definition and characteristics of nonlinear thinking and nonlinear-graph were analyzed,pattern design based on nonlinear thinking and its practical design and application were proposed.At the same time,combined with the theory and principle of nonlinear thinking,problems and application results in actual design process were discussed.

non-linear thinking;fractal theory;pattern design

TS941.2

A

1673-0356(2017)12-0042-03

2017-10-25

国家自然科学基金青年科学基金项目(61503154);江苏省研究生教育教学改革研究与实践课题(JGLX16_047);江南大学本科教育教学改革研究一般项目(JG2015041)

唐 颖(1983-),女,湖南永州人,博士,副教授,主要研究方向为服装设计与品牌,E-mail:9984874@qq.com。