大功率风电制动器制动稳定性研究

沙智华,薛春燕,尹 剑,刘 宇,马付建,张生芳

(大连交通大学 机械工程学院,辽宁 大连 116028)

大功率风电制动器制动稳定性研究

沙智华,薛春燕,尹 剑,刘 宇,马付建,张生芳

(大连交通大学 机械工程学院,辽宁 大连 116028)

风电制动器是大功率风力发电机组制动系统中不可或缺的配套装置,其制动稳定性直接影响到风机制动系统的正常运行.基于风电制动器刚柔耦合动力学模型,仿真分析了不同初始制动转速、制动力、制动盘-闸片摩擦系数下大功率风电制动器的振动特性.根据影响振动的两个主要因素——加速度变化率和振动动能,得出风电制动器制动稳定性判定方法,并利用该方法对制动器制动稳定性进行了研究.通过风电制动器惯性试验台的试验结果,验证了所建立的风电制动器刚柔耦合模型的准确性,进而间接验证了制动稳定性判定结果的准确性.该研究为大功率风电制动器设计、制动参数匹配优化及制动可靠性分析提供参考.

风电制动器; 刚柔耦合多体动力学; 制动参数; 制动稳定性

风电制动器是风力发电机组中制动系统的重要组成部分,其作用是使风机系统适时减速直至停止[1].由于开始制动时,风机主轴转速很高,制动器在制动过程中会产生强烈振动,导致制动过程中制动盘与闸片无法稳定接触,严重影响了制动器的制动稳定性,而且剧烈振动会加剧制动盘与闸片的磨损,降低制动器的寿命.此外,高频振动产生的噪声会对环境造成污染[2-3],还会让操作者产生不安的情绪[4],存在较大的安全隐患[5].因此,风电制动器制动过程中振动与噪声的存在会严重影响风电机组安全、高效的运行[6].

本文通过动力学方法研究了初始制动转速、制动力、制动盘-闸片摩擦系数对制动器振动特性的影响,并通过所建立的风电制动器制动稳定性判定方法对其制动稳定性进行判定,进而找到减小振动、降低噪声、可靠制动的途径.本文所采用的动力学研究方法与传统的有限元复模态分析方法仅从模态耦合的角度消除振动相比,能够进一步考虑摩擦、制动压力和制动转速等重要制动参数对制动的影响[7-8].本文的判定结果可进一步为风机制动系统后续动力学分析及风机制动系统参数匹配优化提供参考.

1 制动器制动稳定性判定方法

本文中制动器的制动稳定性主要由制动盘的振动来表征,而制动盘的振动可从振动学的角度来考虑.在研究列车运行平稳性时,Sperling通过振动台架试验揭示了影响振动的两个主要因素是振动体加速度的变化率和振动动能[9-10].因此,可从这两个因素出发分析制动盘的振动稳定性.

在制动过程中,制动盘轴向加速度的变化率a′可表示为

a′=z‴=F′/m

(1)

式中:z为制动盘轴向的振动位移;F为制动盘轴向受力;m为制动盘的质量.假设制动盘的轴向振动为简谐振动,振动位移可写为

z=z0sinωt

(2)

式中:ω为角频率;t为制动时间;z0为最大振幅.那么,加速度的变化率为

a′=z‴=-z0ω3cosωt

(3)

则加速度变化率的最大幅值为

|z‴|max=z0ω3=z0(2πf)3

(4)

式中:f为振动频率.式(4)反映了制动盘轴向振动的加速度变化率.制动盘轴向振动的最大动能Ed可表示为

即

2Ed/m=(z02πf)2

(5)

式(5)反映了制动盘振动的动能.

为了综合考虑加速度的变化率、动能对制动盘振动的影响,把振动过程中反映制动盘的加速度变化率和动能的量的乘积,作为衡量制动盘振动稳定性的指标.

由于Sperling的列车运行平稳性指标中加权了人对加速度敏感的频率成分,突出强调了人体感受强烈的加速度频段,而对于风电制动器的制动过程,需要突出强调的是制动器的制动效能,而制动过程中制动盘的轴向加速度的均方根值(加速度的有效值)是判定制动盘与闸片是否持续接触的值,最能反映制动盘的振动情况.由此,得到风电制动器制动过程中制动盘振动稳定性判定式为

(6)

式中:rms(ɑ)为制动过程中制动盘轴向加速度的均方根值.

式(6)只适用于频率、振幅不变的单一振动.实际上,制动器制动时制动盘的振动是随机的,即振动频率和振幅都是随时间变化的,可将仿真得到的制动盘振动加速度按频率分解,进行频谱分析[11],求出每段频率范围的振幅值;然后对每一频段计算各自的稳定性指数wi,再求出全部频段内总的稳定性指数W.由此可得

制动器制动稳定性的判定式为

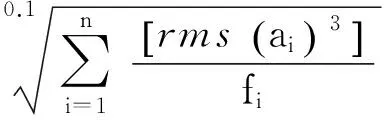
(7)

该制动稳定性判定式包含了制动盘轴向振动的加速度变化率和振动动能.制动过程中W值越大,加速度变化就越剧烈,振动的动能越大,表明制动稳定性越差.

2 刚柔耦合多体动力学模型

为了研究风电制动器的制动稳定性,需要建立制动器的刚柔耦合模型进行制动过程多体动力学仿真,进而探究其制动振动特性.

2.1 刚柔耦合多体动力学模型的建立

风电制动器的主要部件包括制动盘、闸片、制动钳、推杆装置(推杆套筒、补偿螺母)、活塞装置(活塞、补偿螺杆)等,如图1所示.风电制动器的制动过程是由液压保持和机械制动两部分联合完成的[12].当风力发电机组正常运转时液压油进入活塞,此时制动器处于开闸状态.当风电机组需要制动时,油液回退,受压弹簧推动活塞装置、推杆装置致使闸片压紧制动盘,此时制动器处于闭闸状态并实现制动.

图1 制动器整机模型Fig.1 The whole model brake

由于制动器制动稳定性体现在制动盘上,所以制动盘属于此次研究的核心部件.在制动时制动盘受到离心力、制动摩擦力等因素影响,会导致其发生扭转、翘曲变形,进而产生振动,对制动器制动效能的影响较大,因此,需要对制动盘进行柔性化[13].为了减小计算量,将其他受影响较小的部件视为刚体或者以等效质量处理.图2所示是柔性化后的制动盘.中间网状部分为柔性体的刚性区域即柔性体与刚性体连接的部分.

图2 柔性化后的制动盘Fig.2 Flexible disc

将简化后的制动器模型导入动力学软件ADAMS中,用柔性制动盘替换刚性制动盘,对各个零件定义质量、位置、转动惯量等构件属性[14],并在具有相对运动的零部件之间施加符合实际工况的约束关系,如表1所示.各构件属性及构件间约束关系定义完成后,得到制动器的刚柔耦合动力学仿真模型,如图3所示.

2.2 刚柔耦合仿真模型的试验验证

利用风电制动器惯性试验台,在环境温度为10 ℃、湿度为30%的条件下进行制动试验,主轴与飞轮的初始制动转速为800 r/min,制动盘-闸片摩擦系数为0.3,制动力为17 000 N,转动惯量为600 kg·m2.通过试验台的传感器和放大器采集并记录下制动过程中制动力矩、角速度与制动时间的关系曲线,并将试验结果与仿真结果进行对比,如图4和图5所示.

表1 各主要零件间运动副关系Tab.1 The kinematic relationship between the main parts

图3 简化后的制动器刚柔耦合动力学模型Fig.3 Simplified rigid-flexible dynamic model of brake

图4 随时间变化的制动盘角速度Fig.4 The angular velocity of brake disc with time

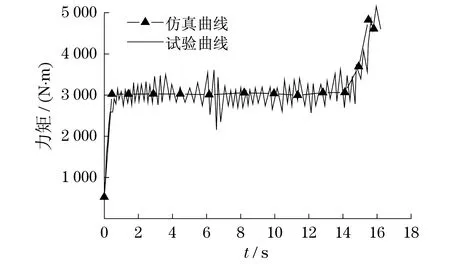
图5 随时间变化的制动盘制动力矩Fig.5 The brake torque of brake disc with time

图4是制动盘的角速度随时间变化的试验与仿真曲线.由图4可看出,惯性试验台的实际制动时间为16.50 s,而仿真制动时间为15.92 s,仿真结果的误差率仅为3.52%.图5是制动盘的制动力矩随时间变化的试验与仿真曲线.从图5中可看出,试验与仿真的制动力矩随时间的变化曲线趋势基本一致.所不同的是由于仿真中摩擦系数为定值,所以力矩曲线不像实际制动中那样波动.在初始制动时由于制动力的突然加载,制动力矩会突变;在制动即将结束时,制动盘与闸片由动摩擦转变为静摩擦,摩擦系数增大使得制动力矩有一个明显的上升.由此可见,所建立的仿真模型可以较好地反映制动器的实际工况,该刚柔耦合模型的准确性也进一步得到了验证.

3 制动仿真及稳定性的判定

3.1 不同参数下的制动仿真

对制动器的刚柔耦合模型在不同制动力、制动盘-闸片摩擦系数、初始制动转速条件下进行动力学仿真,仿真工况参数如表2所示.

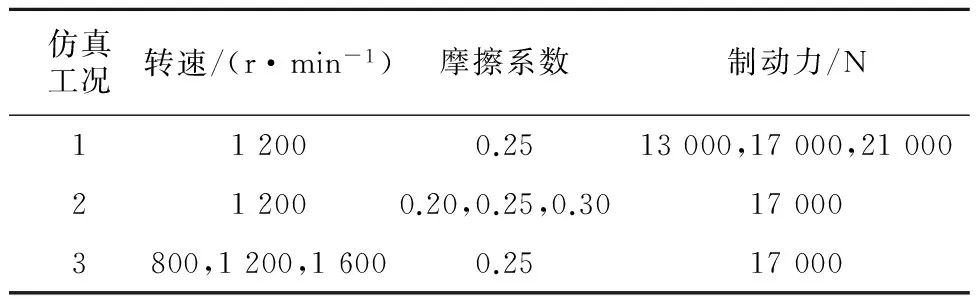
表2 仿真工况参数表Tab.2 The working conditions and parameters in the simulation

3.1.1 不同制动力的制动动力学仿真

图6是制动盘初始制动转速为1 200 r/min,制动盘-闸片摩擦系数为0.25,制动力分别为13 000,17 000,21 000 N时制动盘轴向的加速度-时间曲线图.

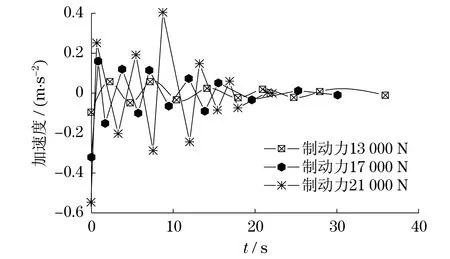
图6 不同制动力下的制动盘轴向加速度-时间曲线Fig.6 The axial acceleration-time curve of brake disc in different braking force

由图6可知,制动盘受到的制动力越大,制动盘轴向加速度值就越大,制动器的振动也就越剧烈.

3.1.2 不同制动盘-闸片摩擦系数的制动动力学仿真

图7是制动盘初始制动转速为1 200 r/min,制动力为17 000 N,制动盘-闸片摩擦系数分别为0.20,0.25,0.30时制动盘轴向的加速度-时间曲线图.

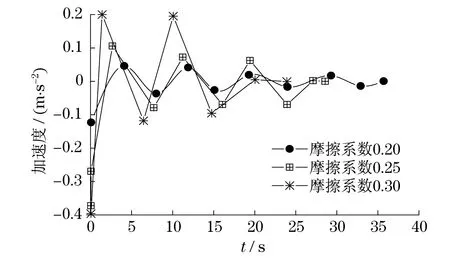
图7 不同制动盘-闸片摩擦系数下制动盘轴向加速度-时间曲线

由图7可知,制动盘-闸片摩擦系数越大,制动盘轴向加速度值就越大,制动器的振动也就越剧烈.

3.1.3 不同初始制动转速的制动动力学仿真

图8是制动力为17 000 N,制动盘-闸片摩擦系数为0.25,初始制动转速分别为800,1 200,1 600 r/min时制动盘轴向的加速度-时间曲线图.

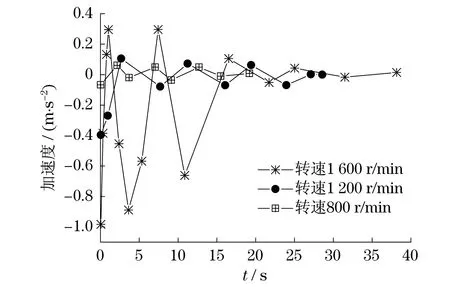
图8 不同转速下的制动盘轴向加速度-时间曲线Fig.8 The axial acceleration-time curve of brake disc in different rotation rate

由图8可知,制动盘的初始制动转速越大,制动盘轴向加速度值就越大,制动器的振动也就越剧烈.

3.2 不同参数下的制动稳定性判定

根据制动器制动稳定性判定式(7)可知,为了得到不同制动力、制动盘-闸片摩擦系数、初始制动转速下的制动稳定性,需要从仿真结果中提取相应工况下制动盘不同频率对应的加速度幅值,并求其均方根值,所得到的稳定性指数如表3所示.利用单一变量法分别研究制动器在不同制动力、摩擦系数、初始制动转速下的制动稳定性.

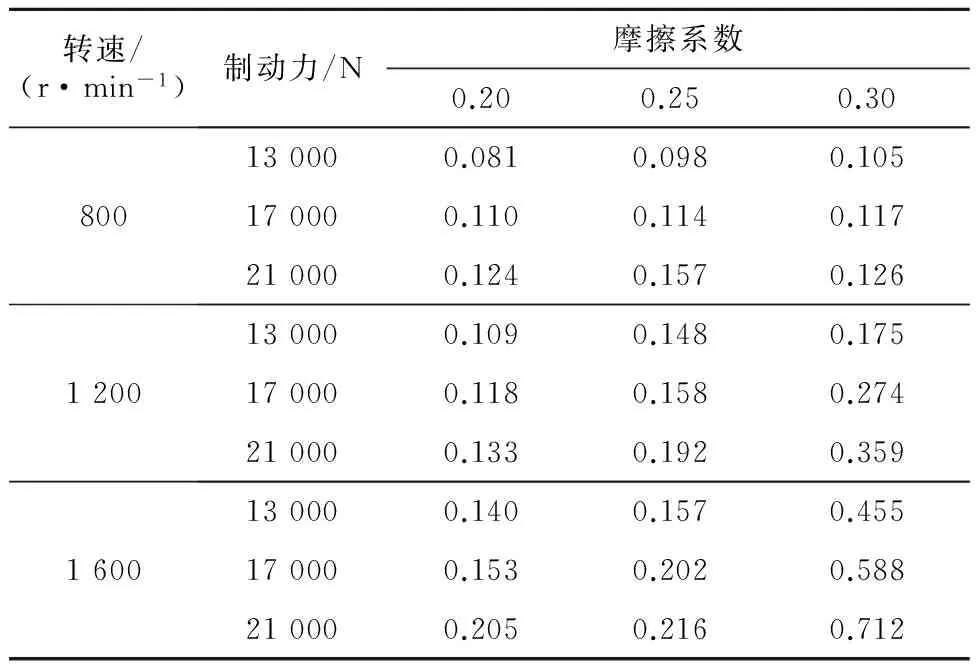
表3 稳定性指数表Tab.3 Index for stability

3.2.1 制动力对制动稳定性影响

将不同制动参数下制动盘的轴向加速度-时间仿真结果进行频谱转化,并对各频段进行制动稳定性评估,得到全部频段内总的制动稳定性指数随各制动参数变化的曲线,如图9所示.

由图9知,在制动盘-闸片摩擦系数、初始制动转速恒定的情况下,随着制动力的增大,制动器制动稳定性指数增大,即制动稳定性变差.这是由于在一定的初始制动转速、制动盘-闸片摩擦系数下,制动力越大,摩擦力随时间变化呈现的波动就越明显,即粘滑现象越严重而造成的.因为粘滑过程中粘滞与滑动的交替出现能够引发制动盘的剧烈振动.

3.2.2 制动盘-闸片摩擦系数对制动稳定性影响

同理,得到全部频段内总的制动稳定性指数随制动盘-闸片摩擦系数变化的曲线,如图10所示.

由图10知,在制动力、初始制动转速恒定的情况下,随着制动盘-闸片摩擦系数的增大,制动器制动稳定性指数增大,即制动稳定性变差.这是由于在一定的初始制动转速、制动力下,制动盘-闸片随着摩擦系数增大,接触摩擦力增大,瞬时振动有较大的振幅,引起自激振动,降低了制动器的制动稳定性.

3.2.3 初始制动转速对制动稳定性影响

由图9和图10知,在制动盘-闸片摩擦系数、制动力恒定的情况下,随着初始制动转速的增大,制动器制动稳定性指数增大,即制动稳定性变差.这是由于在一定的制动盘-闸片摩擦系数、制动力下,初始制动转速增大时,制动器振动的高频成分减少,振动频率更接近于制动器的固有频率,即增大了低频抖动与共振的几率,制动过程中制动器的振动就越剧烈.而且初始制动转速增大,单位时间内制动盘与闸片间的接触划擦距离增大,所造成的粗糙表面间冲击次数增加,冲击强度增大也会加剧制动器的振动.

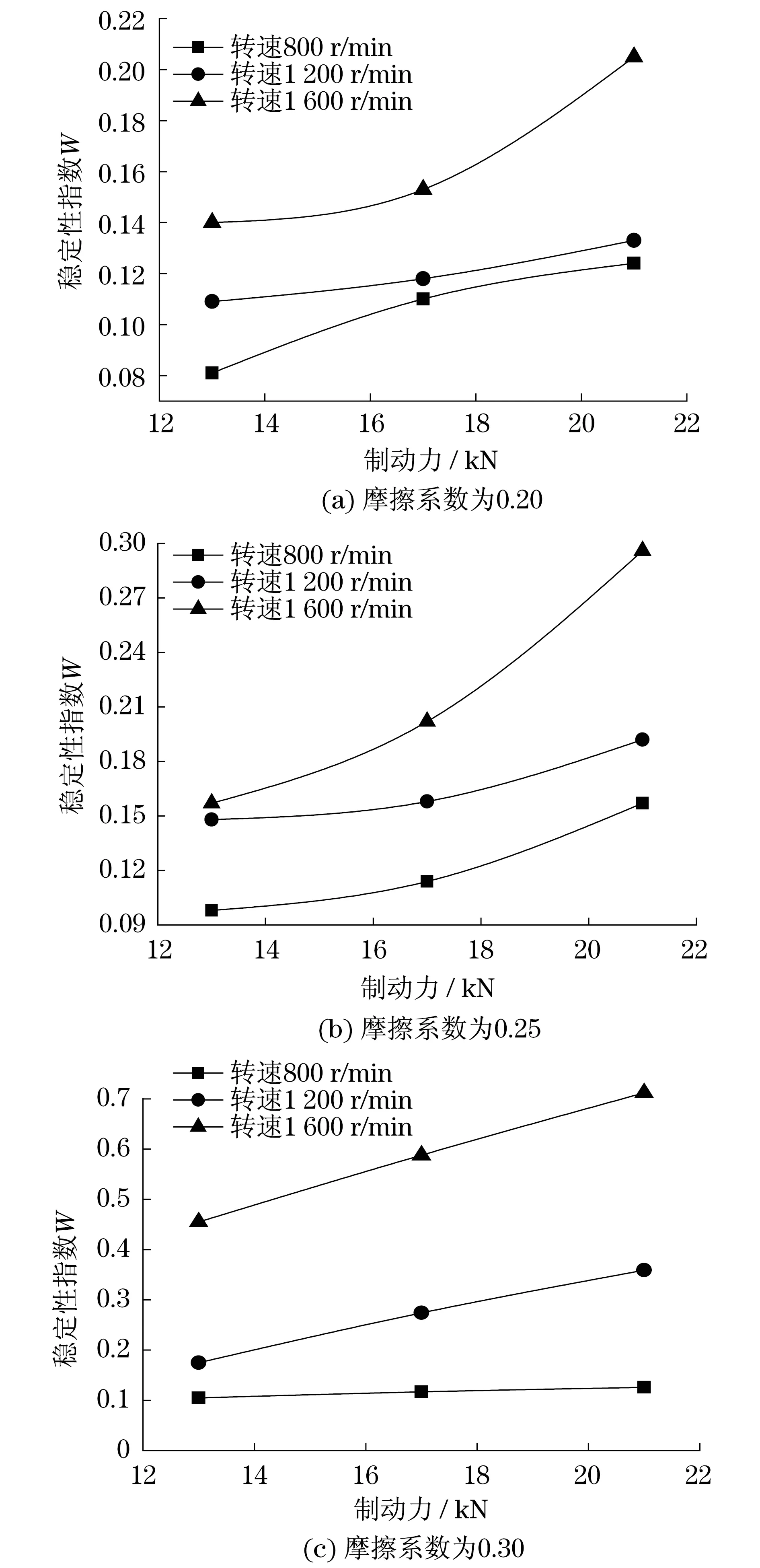
图9 随制动力变化的制动稳定性指数Fig.9 The stability index for braking with the change of braking force

制动力、制动盘-闸片摩擦系数、初始制动转速越大,制动器的制动振动稳定性越差;反之,制动器的振动就会相对较小,但制动器无法实现有效制动.所以,制动参数的选择必须能够使制动器有效且可靠的制动.

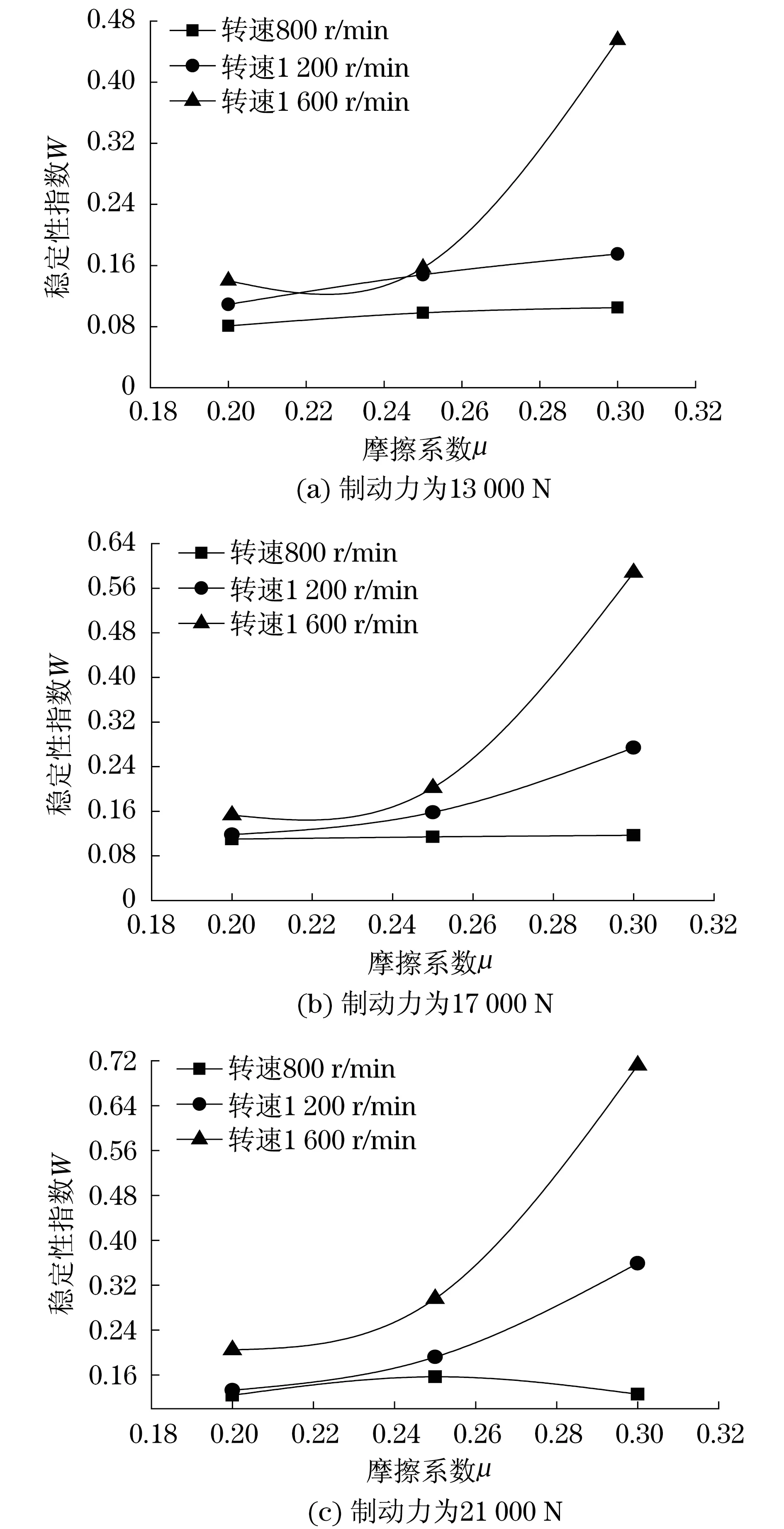
图10 随制动盘-闸片摩擦系数变化的制动稳定性指数Fig.10 The stability index for braking with the change of friction coefficient of disc-pad

3.3 制动器制动稳定性评估

按照上述结论,制动参数取值越小制动盘的振动越稳定,进而制动器的制动效能也就越好.但是制动参数取值太小,所需制动时间就会过长,制动器无法实现按需制动,将会造成无法预测的安全问题.一般情况下,风电制动器的设计标准是初始制动转速为800 r/min时,有效制动时间小于25 s;1 200 r/min时,有效制动时间小于35 s;1 600 r/min时,有效制动时间在45 s以内.根据制动仿真结果得到了各工况下制动时间,如表4所示.

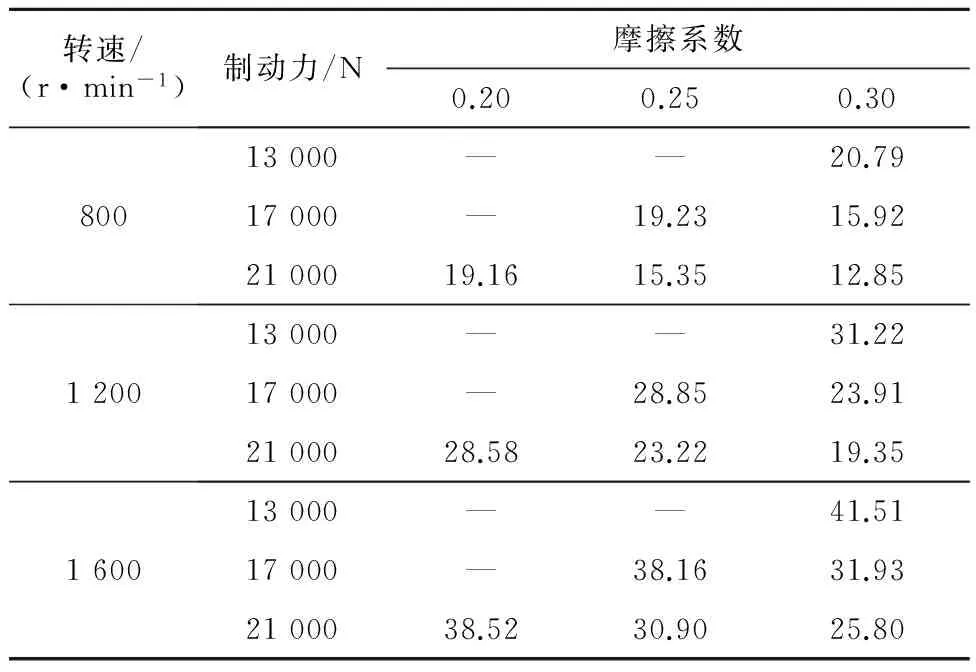
表4 各工况下制动时间Tab.4 Braking time under different working conditions

注:“—”表示超出了有效制动时间范围的制动时间.

由表3和表4不同工况下制动稳定性指数与制动时间的综合考虑,最终选择制动效果最优的制动参数匹配方案.当所设计制动盘-闸片摩擦系数为0.2时,由制动稳定性评估方法得到制动器的初始制动转速推荐为1 200 r/min,制动力推荐为21 000 N;当所设计制动盘-闸片摩擦系数为0.25时,由制动稳定性评估方法得到制动器的初始制动转速推荐为1 600 r/min,制动力推荐为17 000 N;当所设计制动盘-闸片摩擦系数为0.3时,由制动稳定性评估方法得到制动器的初始制动转速推荐为800 r/min,制动力推荐为13 000 N.这种参数匹配优化将为不同工况下大兆瓦级风机制动器的有效制动提供坚实的理论基础.

4 结论

大兆瓦级风电制动器的振动主要体现在制动盘的振动上,本文通过建立风电制动器刚柔耦合模型,对该模型在不同参数下的制动情况进行仿真分析,得出制动器振动特性规律,并进一步对制动器的制动稳定性进行评估,结论如下:

(1) 基于Sperling振动平稳性判定方法,以制动盘轴向加速度的均方根值及振动动能的量作为衡量制动盘振动稳定性的指标,提出风电制动器制动稳定性判定方法,仿真与试验结果验证了稳定性判定方法的合理性.

(2) 由仿真计算与稳定性分析可知,随着制动力的增大,制动器的制动稳定性减小;随着制动盘与闸片间摩擦系数的增大,制动器的制动稳定性减小;随着初始制动转速的增大,制动器的制动稳定性减小.

(3) 当制动盘-闸片摩擦系数确定后,本文的研究方法可推荐合理的制动力及初始制动转速,同时满足制动稳定性和有效制动时间的要求,为大功率风电制动器设计、制动参数匹配优化及制动可靠性分析提供参考.

[1] 王涛,朱文坚.摩擦制动器-原理、结构与设计[M].广州:华南理工大学出版社,1992:1-89.

WANG T,ZHU W J.Friction brake-the principle,structure and design[M].Guangzhou:South China University of Technology Press,1992:1-89.

[2] HIKAROMIS S.Study of brake noise[J].Mitsubishi Tech Review,1968,5(1):23-28.

[3] HEILIG J.Stability of a nonlinear brake system at high operating speeds[J].Tribol,2010(6):119-123.

[4] 余为高,于学华.应用有限元法对盘式制动器制动噪声分析[J].科学技术与工程,2009,9(12):2334-2336,2339.

YU W G,YU X H.Analysis of disc brake noise based on finite element methods[J].Science Technology and Engineering,2009,9(12):2334-2336,2339.

[5] 代昌举.汽车盘式制动器振动与噪声产生机理及传递路径分析[D].沈阳:东北大学,2014.

DAI C J.Analysis on generation mechanism and transfer path of vibration and noise of automotive disc brake[D].Shenyang:Northeastern University,2014.

[6] LBRAHIM R A.Friction-induced vibration,chatter,squeal,and chaos-Part 77:dynamics and modeling[J].Applied Mechanics Reviews,1994,47(7):227-253.

[7] OUYANG H,NACK W,YUAN Y,et al.Numerical analysis of automotive brake squeal:a review[J].Int J Vehicle Noise and Vibration,2005,1(3/4):207-231.

[8] 宁晓斌,张文明.盘式制动器振动的多体动力学分析[J].有色金属,2004,56(4):119-121.

NING X B,ZHANG W M.Multi-body dynamic simulation for analysis of disc brake vibration[J].Nonferrous Metals,2004,56(4):119-121.

[9] 詹斐生.平稳性指标的历史回顾(上)[J].铁道机车车辆,1994(4):43-52.

ZHAN F S.A historical review of stationarity index(part one)[J].Railway Locomotive & Car,1994(4):43-52.

[10] 严隽毫.车辆工程[M].2版.北京:中国铁道出版社,1999.

YAN J H.Vehicle engineering[M].2nd ed.Beijing:China Railway Publishing House,1999.

[11] 方戍,阙兴贵,胡斌.基于Sperling指标的消防灭火机器人运行品质判定[J].机械科学与技术,2011,30(12):2120-2123.

FANG S,QUE X G,HU B.Grading fire robot operation quality using sperling indexes[J].Mechanical Science and Technology for Aerospace Engineering,2011,30(12):2120-2123.

[12] 熊礼俭.风力发电新技术与发电工程设计、运行、维护及标准规范实用手册[J].北京:中国科学文化出版社,2005.

XIONG L J.Handbook of new technologies for wind power generation and design,operation,maintenance and standard specification for power generation engineering[M].Beijing:China Science and Culture Press,2005.

[13] 张力,谷正气,李伟平,等.基于刚柔耦合的盘式制动器振动仿真分析[J].汽车工程,2011,33(3):217-221.

ZHANG L,GU Z Q,LI W P,et al.Simulation and analysis on disc brake vibration based on rigid-flexible coupling[J].Automotive Engineering,2011,33(3):217-221.

[14] 李增刚.ADAMS入门详解与实例[M].北京:国防工业出版社,2006:205-221.

LI Z G.Introduction and examples of ADAMS entry[M].Beijing:National Defense Industry Press,2006:205-221.

Research on braking stability for large-power wind turbine brake

SHAZhihua,XUEChunyan,YINJian,LIUYu,MAFujian,ZHANGShengfang

(School of Mechanical Engineering, Dalian Jiaotong University, Dalian 116028, Liaoning, China)

Wind turbine brake whose stability directly affects the normal running of the wind turbine brake system,is an indispensable matched device in the braking system of large-power wind turbine.The vibration characteristics of large-power wind turbine brake are got by simulating and analyzing in different initial rotational speeds for braking,braking force and friction coefficient between the brake disc and pads,based on the rigid-flexible coupling dynamic model.The judgement formula of vibration stability for barking,which is used for studying the vibration stability of barking for the wind turbine brake,is obtained by the twin main factors that affect the vibration-the change rate in acceleration and kinetic energy of vibration.The accuracy of the rigid-flexible coupling multi-body dynamics model for the wind turbine brake is verified by the test results in the inertia test-bed of wind turbine brake.Furthermore,the accuracy of judgement results on barking stability is attested indirectly.This study will offer references to the design of wind turbine brake,optimization of braking parameters matching and analysis of braking reliability.

wind turbine brake; rigid-flexible coupling multi-body dynamics; braking parameters; braking stability

国家自然科学基金资助项目(51675075,51475066);辽宁省自然科学基金资助项目(2015020114)

沙智华(1973—),女,教授.E-mail:zhsha@djtu.edu.cn

刘 宇(1982—)，男，副教授.E-mail:liuyu_ly12@126.com

TH 164

A

1672-5581(2017)05-0389-07