计及分布式电源渗透率变化的变电站动态扩展规划

刘 洪, 王 博, 葛少云, 郑 楠, 郭 力

(智能电网教育部重点实验室(天津大学), 天津市 300072)

计及分布式电源渗透率变化的变电站动态扩展规划

刘 洪, 王 博, 葛少云, 郑 楠, 郭 力

(智能电网教育部重点实验室(天津大学), 天津市 300072)

针对规划区域在不同发展阶段分布式电源(DG)渗透率由低到高变化场景下的源网荷协调匹配问题,提出了一种有源配电网变电站动态扩展规划方法。首先,考虑变电站滚动投入效应及规划期内剩余价值差异,建立了一种计及DG渗透率的变电站动态扩展规划模型。其次,考虑负载均衡度和DG置信容量对变电站供电范围划分的影响,提出了加权Voronoi图算法的罚函数、凹凸性和方向性改进方法。然后,提出了基于遗传算法和启发式算法的有源配电网变电站动态扩展规划求解方法,得到有源配电网变电站建设顺序。最后,通过实例说明了所述方法的科学性和实用性。

渗透率; 动态扩展规划; 改进加权Voronoi图; 遗传算法; 启发式算法

0 引言

变电站规划问题可以分为旨在满足规划目标年的负荷需求的静态规划和旨在满足各发展阶段持续增长的负荷需求的动态扩展规划[1]。根据国内外先进的规划理念,应当首先实现远景目标年的电网静态规划,进而结合电网现状逐步实现近中期中间年的电网动态扩展规划[2]。结合这一规划思路,本文以负荷饱和年作为远景目标年,并基于目标年变电站选址定容结果,针对中间年变电站动态扩展规划(SDEP)开展研究。该问题在时间轴上涉及了多个时间节点,各时间节点的规划结果之间也存在着较大的关联性,复杂程度较高。

目前,SDEP方面的研究还相对较少,在负荷发展预测与在时间尺度上化简问题等方面也缺少完备的解决方案。文献[3-5]提出了用于SDEP问题的混合整数线性规划模型,将非线性公式有效线性化,并用商业求解器解决混合整数线性规划模型。文献[6]给出了解决SDEP的遗传算法,通过区分短、长期规划,使用遗传算法根据动态策略解决变电站多阶段规划问题。文献[7-9]提出了混合启发式和学习自动机算法,利用静态和动态规划对变电站进行选址、定容和定时。上述文献提出的SDEP模型以整个规划期投资最小为目标函数,忽略了规划期结束时变电站的剩余价值,经济性计算不够精确;模型求解法侧重于求取变电站建设时序,对变电站供电范围的处理较粗糙,无法保证变电站负载均衡性。

近年来,越来越多的可再生能源作为分布式电源(DG)接入配电网,DG供应负荷的能力逐步提升。但由于其波动特性,DG对传统配电网负荷需求产生的影响比较复杂,现阶段变电站扩展规划需重点解决这一问题。目前,有少数变电站规划考虑了DG的影响,文献[10]利用DG的时序特性修正负荷的时序需求并考虑负荷与DG的不确定性设置容量裕度系数,进而建立了变电站时序容量约束,其中利用系数处理负荷与DG不确定性的方式较为粗糙;文献[11]利用基于可靠性的DG置信容量评估得到了等效的负荷需求减少量,进而更新了变电站容量约束,但该方法侧重分析在时间层面DG的电源替代特性对负荷需求产生的影响,忽略了在空间上负荷需求变化对变电站供电范围的影响。

针对以上问题,本文提出了计及变电站滚动投入效应及规划期内剩余价值差异的经济性计算方法,并建立了计及DG渗透率的SDEP模型;提出了加权Voronoi图算法的罚函数、凹凸性和方向性改进方法,以获取满足模型约束的变电站供电范围;然后,提出了基于遗传算法和启发式算法的有源配电网SDEP求解方法,得到有源配电网变电站建设顺序;最后,通过实际算例对比分析,说明了本文方法的科学性和实用性。

1 考虑DG的SDEP模型

1.1 目标函数

目标年变电站规划根据饱和负荷年的负荷需求确定变电站站址站容,即得到变压器的最终状态。本文SDEP是基于目标年变电站规划结果优化中间年变电站投建和扩容时间。为满足饱和负荷年的负荷需求,所有变压器都应完成建设,因此,变电站投建和扩容时间将不影响饱和负荷年以后变电站的经济性。由于变压器存在固定使用年限,变电站内变压器将循环更迭滚动投入。变压器首次投建时间不同,则其在规划期结束时的剩余寿命不同,即剩余价值不同[12]。经济学认为,如果固定资产可继续使用,可将剩余价值作为另一个方案。因此,中间年变电站规划方案投资成本应为规划周期内的等效投资成本,即应减去变压器规划期结束后的剩余价值。

minC=Cstation+Cfeeder+CCQ

(1)

(2)

(3)

(4)

其中,定义DG渗透率M为:

(5)

式中:PL为负荷最大值;PDG为DG置信容量,本文应用文献[13]与文献[14]的光伏与风机时序模型,并采用文献[15]基于可靠性准则及考虑负荷特性的DG置信容量评估方法得到DG置信容量评估结果。

1.2 约束条件

传统的变电站规划中,根据N-1原则确定变电站的负载率,进而建立负荷与变电站负载能力间的不等式约束(容量约束)[16];根据电压等级和负荷密度建立变电站供电半径约束[17]。考虑DG接入配电网后,光伏、风机等承担一部分负荷,网供负荷需求降低;加入DG的局部区域负荷密度等效降低,在该方向的变电站供电半径增加。因此,本文考虑DG的影响建立新的容量和供电半径约束。具体约束条件如下。

1)变电站建设顺序约束

(6)

2)变电站容量约束

(7)

3)变电站网供负荷均衡

i=1,2,…,N,t=1,2,…,T

(8)

式中:max(Ei,t)/min(Ei,t)为在第t阶段变电站网供负荷均衡度;Ei,t为第t阶段变电站i的网供负载率。

4)变电站供电半径约束

li,j≤Ri,tψi,t,j

(9)

式中:Ri,t为第t个阶段变电站i传统配电网中的供电半径限制;ψi,t,j为第t个阶段变电站i考虑DG后在负荷点j方向的半径变化因数,影响负荷点j的DG置信容量越大,ψi,t,j取值越大,具体计算如下。

ψi,t,j=

(10)

(11)

式中:Gi,t为第t个阶段向变电站i供电的DG集合;Si,t,g和Ri,t,g分别为第t个阶段向变电站i供电的DG节点g的装机容量与等效供电半径;li,g为变电站i与DG节点g的距离;ρi,t为第t个阶段变电站i供电范围内的负荷密度。

5)变电站供电范围不交叉

(12)

式中:ηi,t,j为用于判断第t个阶段负荷点j是否由变电站i供电的二进制变量,1表示是,0表示否;δi,t,g为用于判断第t个阶段DG节点g是否向变电站i供电的二进制变量,1表示是,0表示否。

具体的模型求解框架如附录A图A1所示。

2 加权Voronoi图的定义及改进

1.2节中第2至第5个约束条件均需要在变电站供电范围划分时进行限制和判断。本文采用加权Voronoi图算法划分变电站供电范围,并在传统加权Voronoi图的基础上进行改进以达到约束条件的要求。

2.1 传统加权Voronoi图

加权Voronoi图是常规Voronoi图的扩展[18],定义加权Voronoi图如下。

假设Q={q1,q2,…,qn},3≤n<∞为平面欧氏空间上的一个点集,点qi的权值ωi(i=1,2,…,n)为n个正整数,那么围绕n个点将平面空间做一个分割,划分至控制点qi的空间V(qi,ωi)具有以下性质:

V(qi,ωi)={x∈V(qi,ωi)|ωid(x,qi)≤

ωjd(x,qj)，j=1,2,…,n,j≠i}

(13)

式中:d(x,qi)和d(x,qj)分别表示平面上的一点x与qi和qj间的欧氏距离,其中,qi≠qj,i≠j;ωid(x,qi)为点x与qi的加权距离。

以N个变电站作为N个控制点,加权Voronoi图将把规划区域划分为N个Voronoi区域,区域V(qi,ωi)即为变电站的供电范围。变电站容量Si越大,变电站已供负荷量Pi越小,则变电站权值ωi减小以降低负荷点到变电站i的加权距离,进而扩大变电站供电范围。因此变电站权值ωi定义如下:

(14)

式中:τ为衰减系数。

2.2 加权Voronoi图的罚函数改进

由于不同区块负荷增长情况不同,规划期的某个阶段可能出现一些区块负荷密度远低于其他区块的情况。加权Voronoi图划分供电范围时,向低负荷密度区供电的变电站将被赋予极小的权值以得到较大的供电范围。

假设变电站A与B之间距离为a,负荷点O在AB连线的延长线上,OA的距离为OA,OB的距离为OB,且OA>OB。若变电站A与B权值ωA和ωB相差很大,则可能出现加权距离ωAOA>ωBOB的情况,即变电站A与B的供电范围边界发生交叉。因此,变电站的权值应适当加重供电距离对供电范围的影响。

文献[19]从变电站已有供电距离影响剩余供电能力的角度提出了变权重,加重供电距离对供电范围的影响,避免变电站负载率和供电半径越限。但该改进侧重各变电站自身供电半径限制,无法有效改善供电半径较大时供电范围交叉的情况。为解决这一问题,本文提出了加权Voronoi图的罚函数改进,在达到一定供电距离后,增大变电站的权值,有效避免变电站供电范围交叉,具体权值公式如下。

(15)

2.3 加权Voronoi图的凹凸性改进

加权Voronoi图的权值反映负荷分布不均匀、各站额定负载率和供电半径对变电站供电范围的影响[20]。加权Voronoi图划分供电范围是一个不断迭代的过程,通过反复调整变电站的权值来得到满足约束条件的供电范围。变电站的权值控制变电站供电范围边界线的移动,边界线较小的移动也可能导致多个负荷点所属变电站发生变化。因此,变电站权值的控制精度能够满足变电站负载率要求却很难满足变电站网供负荷均衡这一约束。

为解决这一问题,本文提出了加权Voronoi图的凹凸性改进。在加权Voronoi图迭代满足变电站负载率约束后,重新判断两个相邻变电站间边界负荷点的归属问题。将网供负载率较高的分区边界上的负荷从大到小排序,依次判断是否需转移至临近的网供负载率较低的分区以满足负荷均衡的约束。

2.4 加权Voronoi图的方向性改进

DG接入配电网后,分担了配电网部分负荷, DG供电区域的网供负荷需求降低,为保障供电经济性,变电站供电半径应在DG供电区域方向相应增加[20]。因此,各变电站的权值计算如下:

(16)

3 基于遗传算法和启发式算法的有源配电网SDEP

3.1 遗传算法编码

遗传算法中,染色体使用二进制编码并根据变电站变压器个数提出两种不同编码方式来表示变电站投建和扩容的阶段。变电站在目标年有两个变压器则采用两位二进制编码:00表示第一阶段投建;01表示第二阶段投建;10表示第三阶段投建;11表示第四阶段投建。变电站在目标年有三个变压器,则采用四位二进制编码,四位中仅有一位为1表示投建和扩容在同一阶段完成,其中,0001表示第一阶段投建和扩容;四位中仅有两位为1表示在前面阶段投建,后面阶段扩容,其中,0101表示第一阶段投建、第三阶段扩容。这种编码方式保证建设顺序相近个体的编码类似,有利于局部寻优[21]。

上述编码方式将很大程度降低交叉和变异操作后不可行解出现的概率。

3.2 基于遗传算法和启发式算法的求解流程

本文基于遗传算法和启发式算法进行有源配电网SDEP,首先利用遗传算法得到不计及DG的SDEP结果;之后计及 DG的影响,提出启发式算法,结合目标年变电站规划结果(计及DG和不计及DG的目标年站址站容均为已知条件)和不计及DG的SDEP结果,综合分析得到计及DG的SDEP结果。具体流程如下。

步骤1:本文将规划分为四个阶段,首先初始化变电站建设顺序种群。

步骤2:不考虑DG,利用改进加权Voronoi图算法对种群中的个体进行供电范围划分并删除不满足约束的个体。

步骤3:不考虑DG,以目标函数的倒数建立适应度函数,根据精英策略保留精英个体,利用轮盘赌进行选择,以交叉概率pc和变异概率pm对种群进行多点交叉及变异,最终生成新种群。当达到最大迭代次数时结束寻优,输出最小费用和最优个体。

步骤4:建立计及DG和不计及DG的目标年变电站规划结果的变电站对应关系。例如,计及DG的目标年规划结果中变电站8的站址和不计及DG的结果中变电站4的站址的距离最近,则建立对应关系4-8。

步骤5:根据步骤3得到不计及DG时,由目标年回推至初始规划年变电站的削减顺序,结合步骤4得到的变电站对应关系生成计及DG时,由目标年回推至初始规划年变电站的削减顺序。

步骤6:由目标年依次前推,每个中间规划阶段均按照变电站削减顺序进行减容减站,利用改进加权Voronoi图算法划分供电范围判断是否满足约束,若满足约束,则接受对此变电站的处理;

步骤7:重复步骤6直至所有阶段规划完成。

4 算例对比

4.1 基本情况

本算例选用某占地面积63.08 km2的区域,根据用地规划将其分为368个小区进行空间负荷预测,规划期为20年,其负荷饱和年总负荷为744.5 MW,功率因数为0.9。规划区域预测目标年光伏发电额定容量为250.5 MW,风机发电额定容量为126.5 MW。按照规划区负荷发展程度将其分为老城区、第1年投建的新城区和第10年投建的新城区。负荷特性分为居民、商业和工业三种。

368个负荷点的位置、负荷量、DG类型和DG装机容量参见文献[17],规划区发展类型和负荷特性附录A图A2。不同发展类型区域的负荷增长情况如附录A图A3所示。不计及DG与计及DG的目标年变电站站址站容结果见附录A表A1。

4.2 不计及DG的SDEP结果

根据3.2节求解流程可知,不计及DG的SDEP结果是计及DG的SDEP的基础,因此,本节首先不计及DG的影响,利用遗传算法进行配电网SDEP仿真,得到各阶段变电站建设状态以及变电站供电范围,具体如图1所示。图中,小实心圆表示光伏,大实心圆表示变电站,小空心圆表示负荷点,实心三角形表示风机,(x,y)表示平面上点的位置。

图1 不计及DG的SDEP各阶段变电站供电范围Fig.1 Substation power supply range of different stages in SDEP without considering DG

遗传算法在80代左右收敛,不计及DG的SDEP在规划期投资终值为78 913万元。目标年共有8个变电站,装机容量为1 090 MVA,其中,变电站1和变电站2为已有变电站。由图1可知,第一阶段将建设3×50 MVA的变电站5,此阶段共有3个变电站;第二阶段将建设2×50 MVA的变电站4和2×40 MVA的变电站6,此阶段共有5个变电站;第三阶段将建设3×50 MVA的变电站7和3×40 MVA的变电站8,扩容变电站4为3×50 MVA、变电站6为3×40 MVA,此阶段共有7个变电站;第四阶段将建设2×50 MVA的变电站3,完成所有变电站的建设。

4.3 不计及DG规划方案的DG容量价值

4.2节中图1展示了不计及DG的规划方案,变电站的供电范围划分只考虑了负荷与变电站的关系。实际上,DG根据已划分的供电范围及DG位置可确定所属变电站,并发挥其容量价值。因此,本节对DG在图1方案下的容量价值进行评估,具体各阶段变电站装机容量、DG置信容量、DG渗透率、容载比和负载率差值结果如表1所示。

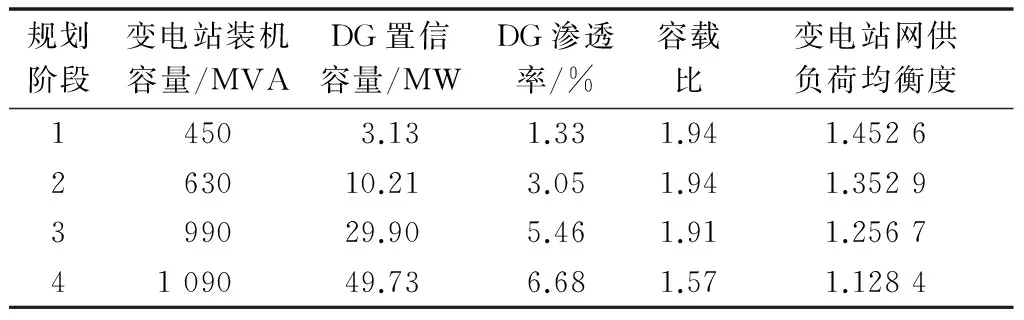
表1 不计及DG的SDEP结果Table 1 SDEP results without considering DG

由表1可知,在这4个规划阶段,DG的置信容量由3.13 MW增加至49.73 MW,DG渗透率也由1.33%提升至6.68%;DG分担部分负荷,变电站容载比相对于自然负荷下的容载比有所提高。

4.4 计及DG的SDEP结果

本节根据计及DG和不计及DG的目标年变电站站址站容结果建立变电站对应关系为:1-1,2-2,3-3,4-4,4-8,5-5,6-6,7-7。结合4.2节得到的结果,利用启发式算法进行计及DG的SDEP。各阶段变电站建设状态及供电范围如图2所示。图中,小实心圆表示光伏,大实心圆表示变电站,小空心圆表示负荷点,实心三角形表示风机。

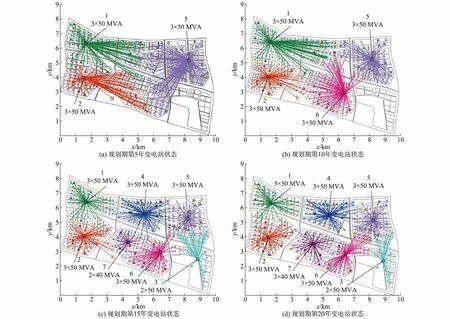
图2 计及DG的SDEP各阶段变电站供电范围Fig.2 Substation power supply range of different stages in SDEP considering DG

计及DG的SDEP在规划期投资终值为49 492万元。目标年共有7个变电站,装机容量为970 MVA,其中,变电站1和变电站2为已有变电站。由图2可知,第一阶段将建设3×50 MVA的变电站5,此阶段共有3个变电站;第二阶段将建设3×50 MVA的变电站6,此阶段共有4个变电站;第三阶段将建设3×50 MVA的变电站4,2×50 MVA的变电站3和2×40 MVA的变电站7,此阶段共有7个变电站;第四阶段将扩容变电站7为3×40 MVA,完成所有变电站的建设。通过图1和图2对比分析可知,计及DG置信容量进行规划将减少或延缓变电站建设,因此,和4.2节相比,本节变电站投资终值降低了37.28%。

4.5 计及DG规划方案的DG容量价值

4.4节中图2展示了计及DG的规划方案,变电站的供电范围划分考虑了负荷、DG与变电站的关系。本节对DG在图2方案下的容量价值进行评估,具体各阶段变电站装机容量、DG置信容量、DG渗透率、容载比和负载率差值结果如表2所示。

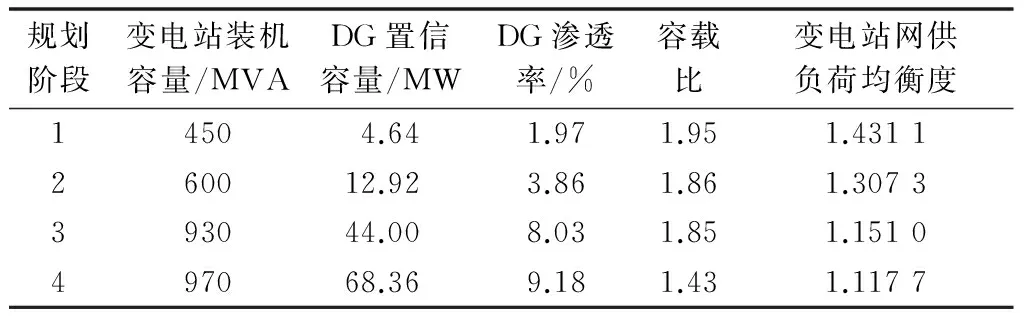
表2 计及DG的SDEP结果Table 2 SDEP results considering DG

由表2可知,有源配电网的4个规划阶段,DG的置信容量由4.64 MW增加至68.36 MW,DG渗透率由1.97%提升至9.18%。

通过表1和表2对比可知,在计及DG置信容量的规划中,第一阶段变电站装机容量不变,容载比提升至1.95;第二阶段变电站装机容量降低30 MVA,容载比降至1.86;第三阶段变电站装机容量降低60 MVA,容载比降至1.85;第四阶段变电站装机容量降低120 MVA,容载比降至1.43。综上,随着DG渗透率的提高,DG分担负荷的比例越来越高,变电站装机容量减少量越来越大,变电站容载比也随变电站装机容量的减少而降低,避免了变电站容量的冗余,保证了变电站建设的经济性。因此,SDEP考虑DG的影响会使规划方案更加合理。

另一方面,在计及DG置信容量的规划中,第一阶段DG的置信容量提升了48.24%;第二阶段DG的置信容量提升了26.54%;第三阶段DG的置信容量提升了47.16%;第四阶段DG的置信容量提升了37.46%。此外,变电站在各阶段的网供负荷均衡度均有所改善。因此,变电站供电范围考虑DG的影响会提升DG置信容量并使各变电站网供负荷更加均衡。

4.6 方向性改进的效果

DG渗透率越高加权Voronoi图方向性改进的效果越明显。为具体说明计及DG置信容量后方向性改进的效果,选定DG渗透率最高的第四阶段,对各变电站的半径变化因数Ψi,4,j(1.000 0～1.569 2)进行展示,如图3所示。图中,小实心圆表示负荷点,大实心圆表示变电站,大空心圆表示光伏,空心三角形表示风机。

图3 半径变化因数示意图Fig.3 Schematic diagram of radius change factor

由负荷点颜色可知,在DG越聚集的方向,半径变化因数越大,本文提出的加权Voronoi图方向性改进能较好地反映DG对变电站供电范围的影响。

5 结语

本文以DG置信容量与负荷峰值的比值为DG渗透率并提出了一种计及DG的SDEP方法。与不计及DG的SDEP相比,随着变电站DG渗透率的提高,DG置信容量对变电站装机容量的影响越来越大。

在变电站建设上,充分计及各阶段DG替代特性,减少或延缓了变电站投资,降低了变电站投资终值,保证了变电站建设经济性。在变电站供电范围划分上,提出了加权Voronoi图罚函数和凹凸性改进,保证了满足约束的供电范围划分;充分计及DG置信容量空间上的影响,提出了加权Voronoi图方向性改进,使变电站的供电范围更加合理,均衡变电站网供负荷的同时提升了DG置信容量。

未来在有源配电网SDEP中还可考虑柔性负荷影响、概率性容量充裕度等问题。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

[1] FRANCO J F, RIDER M J, ROMERO R. Robust multi-stage substation expansion planning considering stochastic demand[J]. IEEE Trans on Power Systems, 2016, 31(3): 2125-2134.

[2] GONEN T. Electric power distribution systems engineering[M]. New York, NY, USA: McGraw-Hill, 1986.

[3] JALALI M, ZARE K, HAGH M T. A multi-stage MINLP-based model for sub-transmission system expansion planning considering the placement of DG units[J]. International Journal of Electrical Power & Energy Systems, 2014, 63: 8-16.

[4] JALALI M, ZARE K, HAGH M T. Dynamic expansion planning of sub-transmission substation and defining the associate service area[J]. Electric Power Systems Research, 2014, 116: 218-230.

[5] NAJAFI S, HOSSEINIAN S H, ABEDI M, et al. A framework for optimal planning in large distribution networks[J]. IEEE Trans on Power Systems, 2009, 24(2): 1019-1028.

[6] HAGHIFAM M R, SHAHABI M. Optimal location and sizing of HV/MV substations in uncertainty load environment using genetic algorithms[J]. Electric Power Systems Research, 2002, 63: 37-50.

[7] MAZHARI S M, MONSEF H, ROMERO R. A hybrid heuristic and evolutionary algorithm for distribution substation planning[J]. IEEE Systems Journal, 2015, 9(4): 1396-1408.

[8] RAVADANEGH S N, ROSHANAGH R G. On optimal electric power distribution networks expansion planning[J]. International Journal of Electrical Power & Energy Systems, 2014, 54: 487-497.

[9] RAVADANEGH S N, ROSHANAGH R G. A heuristic algorithm for optimal multistage sizing, siting and timing of MV distribution substations[J]. Electric Power Systems Research, 2013, 105: 134-141.

[10] 李振坤,岳美,胡荣,等.计及分布式电源与可平移负荷的变电站优化规划[J].中国电机工程学报,2016,36(18):4883-4893.

LI Zhenkun, YUE Mei, HU Rong, et al. Optimal planning of substation considering distributed generation and shiftable loads[J]. Proceedings of the CSEE, 2016, 36(18): 4883-4893.

[11] 葛少云,王世举,路志英,等.基于分布式电源置信容量评估的变电站规划方法[J].电力系统自动化,2015,39(19):61-67.DOI:10.7500/AEPS20141202007.

GE Shaoyun, WANG Shiju, LU Zhiying, et al. Substation optimization planning method based on capacity credit evaluation of distributed generator[J]. Automation of Electric Power Systems, 2015, 39(19): 61-67. DOI: 10.7500/AEPS20141202007.

[12] 林仁文,杨熠.中国的资本存量与投资效率[J].数量经济技术经济研究,2013(9):72-88.

LIN Renwen, YANG Yi. A new estimate of China’s capital stock[J]. The Journal of Quantitative & Technical Economics, 2013(9): 72-88.

[13] PARK J, WU L, CHOI J, et al. A probabilistic reliability evaluation of a power system including solar/photovoltaic cell generator[C]// IEEE Power and Energy Society General Meeting, July 26-30, 2009, Calgary, Canada: 3849-3854.

[14] 方鑫,郭强,张东霞,等.考虑天气不确定性的光伏电站置信容量评估[J].电力系统自动化,2012,36(10):27-32.

FANG Xin, GUO Qiang, ZHANG Dongxia, et al. Capacity credit evaluation of grid-connected photovoltaic generation considering weather uncertainty[J]. Automation of Electric Power Systems, 2012, 36(10): 27-32.

[15] 王世举.考虑供电能力提升和分布式电源接入的变电站优化规划[D].天津:天津大学,2015.

[16] 苏海锋,张建华,梁志瑞,等.基于全寿命周期成本的配电网变电站选址定容优化规划[J].电力系统自动化,2012,36(23):59-64.

SU Haifeng, ZHANG Jianhua, LIANG Zhirui, et al. Substation locating and sizing optimization planning based on life cycle cost[J]. Automation of Electric Power Systems, 2012, 36(23): 59-64.

[17] GONZALEZ-SOTRES L, MATEO-DOMINGO C, SANCHEZ-MIRALLES A, et al. Large-scale MV/LV transformer substation planning considering network costs and flexible area decomposition[J]. IEEE Trans on Power Delivery, 2013, 28(4): 2245-2253.

[18] 路志英,葛少云,王成山.基于粒子群优化的加权伏罗诺伊图变电站规划[J].中国电机工程学报,2009,29(16):35-41.

LU Zhiying, GE Shaoyun, WANG Chengshan. Substation location planning of the weighted Voronoi diagram based on particle swarm optimization algorithm[J]. Proceedings of the CSEE, 2009, 29(16): 35-41.

[19] 曹昉,孟琦斌,苗培青,等.基于改进加权Voronoi图和遗传算法的变电站规划[J].电网技术,2015,39(2):511-516.

CAO Fang, MENG Qibin, MIAO Peiqing, et al. Optimal substation planning based on improved weighted Voronoi diagram and genetic algorithm[J]. Power System Technology, 2015, 39(2): 511-516.

[20] 刘洪,王博,李梅菊,等.基于改进加权Voronoi图算法的有源配电网变电站规划[J].电力系统自动化,2017,41(13):45-52.DOI:10.7500/AEPS20160927009.

LIU Hong, WANG Bo, LI Meiju, et al. Substation planning of active distribution network based on improved weighted Voronoi diagram method[J]. Automation of Electric Power Systems, 2017, 41(13): 45-52. DOI: 10.7500/AEPS20160927009.

[21] 熊雄,叶林,杨仁刚.电力需求侧规模储能容量优化和经济性分析[J].电力系统自动化,2015,39(17):42-48.DOI:10.7500/AEPS20131212005.

XIONG Xiong, YE Lin, YANG Rengang. Optimal allocation and economic benefits analysis of energy storage system on power demand side[J]. Automation of Electric Power Systems, 2015, 39(17): 42-48. DOI: 10.7500/AEPS20131212005.

DynamicExpansionPlanningforSubstationConsideringVariationofDistributedGeneratorPermeability

LIUHong,WANGBo,GEShaoyun,ZHENGNan,GUOLi

(Key Laboratory of Smart Grid of Ministry of Education (Tianjin University), Tianjin 300072, China)

Aiming at the problem of coordination of source, network and load in planning area where the permeability of distributed generator varies from low to high at different stages of development, a dynamic expansion planning method for substation with distributed generator penetration is proposed. Firstly, considering the rolling input effect and the residual value difference of substation during the planning period, a dynamic expansion planning model for substation with distributed generator permeability is established. Secondly, considering load balance and the influence of distributed generator capacity on the power supply division of substation, the penalty function, convexity and direction improvement methods of weighted Voronoi diagram algorithm are achieved. Thirdly, the substation dynamic expansion planning method of active distribution network based on genetic algorithm and heuristic algorithm is proposed, and the construction sequence of active distribution network substation is obtained. Finally, an example is given to illustrate the scientific and practicality of the method.

This work is supported by National Key Research and Development Program of China (No. 2016YFB0900401) and National Natural Science Foundation of China (No. 51477116).

permeability; dynamic expansion planning; improved weighted Voronoi diagram; genetic algorithm; heuristic algorithm

2017-06-15;

2017-07-17。

上网日期: 2017-09-19。

国家重点研发计划资助项目(2016YFB0900401);国家自然科学基金资助项目(51477116)。

刘 洪(1979—),男,博士,副教授,主要研究方向:城市智能电网及综合能源系统规划与评估。E-mail： liuhong@tju.edu.cn

王 博(1993—),女,通信作者,硕士研究生,主要研究方向:城市智能电网规划评估。E-mail: dianwuwb@tju.edu.cn

葛少云(1964—),男,教授,博士生导师,主要研究方向:城市电网规划和配电系统自动化等。E-mail: syge@tju.edu.cn

(编辑万志超)