基于神经网络平均影响值的超短期风电功率预测

徐龙博, 王 伟, 张 滔, 杨 莉, 汪少勇, 李煜东

(1. 中国能源建设集团广东省电力设计研究院有限公司, 广东省广州市 510663;2. 南瑞集团公司(国网电力科学研究院), 江苏省南京市 211106;3. 国电南瑞南京控制系统有限公司, 江苏省南京市 210061)

基于神经网络平均影响值的超短期风电功率预测

徐龙博1, 王 伟2,3, 张 滔2,3, 杨 莉1, 汪少勇1, 李煜东1

(1. 中国能源建设集团广东省电力设计研究院有限公司, 广东省广州市 510663;2. 南瑞集团公司(国网电力科学研究院), 江苏省南京市 211106;3. 国电南瑞南京控制系统有限公司, 江苏省南京市 210061)

针对动态神经网络风电功率预测模型输入变量较多、模型复杂的问题,将神经网络和平均影响值方法相结合,提出了一种基于神经网络平均影响值的超短期风电功率预测方法。此方法综合考虑了各输入变量对输出变量(风电预测功率)的外部贡献率和内部贡献率,筛选出了对输出变量贡献率最大的输入变量,建立了一个优化的神经网络超短期风电功率预测模型。实验结果表明,所提模型降低了预测模型的复杂度,减少了测量噪声对预测精度的影响,得到了较好的风电功率预测结果。

风电功率; 超短期预测; 动态神经网络; 平均影响值; 变量筛选

0 引言

准确的风电功率预测是提高风电接入容量、保证电网运行稳定性和经济性的有效手段[1-2]。风电功率预测通常分为短期预测与超短期预测。其中超短期预测是对风电场未来数小时内的出力进行预测,主要用于日内计划滚动,动态调节短期预测误差引起的功率波动,有助于优化调频及旋转备用容量,以及在线优化机组组合与经济负荷调度[3-4]。超短期预测的预测精度对电网运行安全有着重要影响[5-6]。

目前,对风电功率的超短期预测方法主要可分为物理预测方法与统计预测方法[1,5]。由于风力具有非线性、不确定等诸多特性,物理预测的计算过程非常复杂,且往往要依赖数值天气预报的结果,无法适用于需要频繁给出预测结果的超短期风电功率预测,因此超短期风电功率通常采用统计方法进行预测[7],常见的方法包括:持续法[8]、时间序列法[9-10]、支持向量机法[11-13]、神经网络(neural network,NN)法[14-16]等。持续法是将最近一点的功率观测值作为下一点的预测值,该方法具有模型简单、容易实现的优点,但随着时间尺度的增大,预测精度会快速下降。时间序列法则根据风电功率或风速随时间变化的趋势外推,该方法可通过不同的需求设定不同的外推算法,来适应系统不同的动态特性,因此预测精度较持续法要高。但两种方法均有输入数据单一、难以考察其他信息的问题。

支持向量机预测方法和神经网络预测方法是两种典型的人工智能模型预测方法,它们能够通过数据的训练,确定不同变量之间的映射关系,例如可建立以风速与风向为输入,以风电场总功率为输出的预测模型,还可根据输入变量对输出变量的贡献率分析,进行变量筛选和重新组合,使预测模型的实现具有较高的灵活性。

有研究表明[7,17]:在历史数据较为充分的条件下,神经网络预测方法在预测精度和泛化能力上比支持向量机等预测方法更有优势,因此得到了更为广泛的研究和应用。

目前的神经网络风电功率预测方法中所使用的神经网络通常是静态神经网络,无法反映系统的动态特性,当风速、风向发生较大变动时,预测精度会有较大下降。为解决这个问题,本文首先给出一种基于动态神经网络的风电功率超短期预测模型。该预测模型采用风速和风向余弦的导数表征系统的动态特性,采用神经网络表征系统的非线性特性,较完整地描述了系统的动静态特性,在风速变动较大时也具有较高的预测精度。但由于引入了输入变量的导数,当风机数量增加时,预测模型的输入变量个数会大量增多,使得模型变得极为复杂,不适用于大型风电场的功率预测。

为此本文在动态神经网络预测模型的基础上提出了一种基于神经网络平均影响值(NN-MIV)的变量选择方法,通过对输入变量对输出变量的贡献率进行排序,筛选出对预测功率贡献率较大的变量构建新的预测模型,使构建的预测模型结构简单,并具有较高的预测精度。

1 动态神经网络预测原理

目前,大部分的神经网络预测系统采用如下的静态预测模型:

PWP=fNN(V,Dcos)

(1)

式中:PWP为风电场的预测功率;V为各风机所在位置的风速;Dcos为各风机所在位置的风向的余弦值;fNN表示输入输出的非线性函数关系,用静态神经网络来实现。

由式(1)可知,目前常见的神经网络预测方法的输入变量只采用了当前的风速和风向,而没有采用任何动态信息,因此所建立的预测模型无法反映系统的动态特性。这样的预测模型在风速相对稳定的时候能够较好地预测风电功率,但当风速或者风向发生较大变化时,预测精度往往不甚理想。

为了解决这个问题,有研究者采用了动态的神经网络来建立预测模型[18]。但该动态神经网络采用局部反馈时延的神经网络,即采用时延和反馈表征预测系统的动态特性,这种动态神经网络可看作时间序列方法[9]跟神经网络结合的一种方法。文中作者构造了一个以风速、风向等变量和它的历史序列为输入,以预测功率为输出的神经网络,来实现对风电功率的预测。这种动态神经网络用风速、风向等变量的时间序列表征它们未来的变化趋势来预测功率,实际上是将变量的导数等趋势信息隐含在时间序列中,并通过神经网络去拟合出时间序列与未来趋势的隐含关系,因此这种动态神经网络的物理意义不甚清晰,动态特性难以把握,在模型训练时会增加神经网络收敛的难度,影响预测模型的精度。

因此,本文采用如下的动态预测模型:

(2)

风速和风向的导数表征风速和风向的变化趋势,包含风速和风向未来的信息,将这些信息引入风电功率预测模型中使预测模型具有了直观的物理意义。结构合理的静态神经网络可以以任意精度逼近非线性函数关系。因此,理论上来说,将静态神经网络和微分器相结合所构成的动态神经网络可以逼近一般非线性动态系统,将其用于风电功率预测可获得很好的预测效果。

但由于引入了输入变量的导数,使得动态神经网络预测模型的输入变量个数比静态神经网络预测模型增加了2倍。当动态神经网络预测模型应用于大型风电场时,模型的输入变量个数会变得非常巨大,使得模型变得极为复杂,大大增加了神经网络的训练时间。增加的变量也会增加噪声引入的可能性,出现预测精度下降的情况。

为此本文提出了一种基于NN-MIV的变量选择方法,通过平均影响值方法衡量各输入变量对输出变量的外部贡献率,通过神经网络方法衡量各输入变量对输出变量的内部贡献率,结合两种方法,得到较为稳定的贡献率值,可简化预测模型的结构,减少神经网络训练的时间,并有望获得较高的预测精度。

2 NN-MIV变量筛选原理

2.1 平均影响值及外部贡献率

假设式(2)所示预测模型的输入变量个数是p。令这p个变量组成一个自变量向量,并对其进行m次观测,得到X=[x1,x2,…,xm]的自变量空间。相应地,与每一个样本点所对应的因变量可以写为Y=[y1,y2,…,ym]。以m个样本的自变量向量组成的X作为输入,与之对应的向量Y作为输出,组成训练样本集{X,Y}训练神经网络,保存训练好的神经网络。然后对原始训练用的自变量空间作如下变换,依次对各自变量在原值的基础上分别加、减δ(百分数),得到如下2p(i=1,2,…,p)个新的自变量空间:

(3)

(4)

把构造好的新自变量空间依次作为神经网络模型的输入,经网络输出后得到变化样本点中第i(i=1,2,…,p)个输入变量指标变化时与之对应的2p个输出向量:

(5)

(6)

(7)

式中:IMIV,i为变化样本中第i个输入变量指标对输出结果的平均影响值。IMIV,i的符号表示自变量与因变量相关的方向,绝对值大小代表自变量对因变量影响的相对重要性。

进一步计算得到第i个变量xi对输出y的贡献率为:

(8)

这种方法通过预测模型外部输入的变化计算各输入变量对输出变量的贡献率,因此把这种贡献率定义为外部贡献率。

2.2 神经网络及内部贡献率

文中选用的神经网络为三层前向神经网络,其网络一般形式为:

(9)

式中:xi(i=1,2,…,p)为第i个输入;βj(j=0,1,…,q)为从隐含层到输出层的连接权值;ωji为输入层到隐含层的连接权值。

(10)

式中:cov和var分别表示求协方差和求方差函数。

然后,计算隐含层oj对输出y的贡献值:

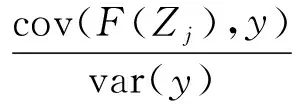
(11)

因此,第i个输入xi对输出y的贡献值为:

(12)

进一步,得到xi对输出y的贡献率为:

(13)

这种方法通过神经网络输入对隐含层的权值的变化和隐含层对输出权值的变化计算各输入变量对输出变量的贡献率,因此把这种贡献率定义为内部贡献率。

2.3 基于NN-MIV的变量选择方法

MIV方法表征了预测模型对外部输入变化的特性,计算得到的贡献率为外部贡献率。但仅考虑模型外部贡献率无法保证筛选出来的输入变量最优,因此需要其他方法来弥补,基于神经网络的内部贡献率计算方法能很好地做到这一点。它利用输入层对隐含层的权值的变化和隐含层对输出层权值的变化计算各输入变量对输出变量的内部贡献率,以避免单一使用外部贡献率造成的贡献率计算不稳定、输入变量选择不可靠等问题。本文结合两种贡献率计算方法,提出了基于NN-MIV综合贡献率的变量选择方法,其综合贡献值表达式定义为:

CNN-MIV,i=|αMIV,iαNN,i|=[C1,C2,…,Cp]T

(14)

进一步,得到xi对输出y的综合贡献率为:

(15)

将内部贡献率与外部贡献率结合可以使预测模型的输入变量贡献率值明显增大易于选择,又可以保证所建模型同时具有较高的外部贡献率和内部贡献率,避免外部贡献率计算不稳定等问题。

3 实验结果与分析

以盐城某风电场的46台风机作为研究对象。图1为所有风机的坐标分布图,从图中可以看出,46台风机的位置呈不规则的散布,很难直接从空间分布中分析各台风机的相关性,也很难直接确定哪些风机的风速、风向数据对预测风电场总功率的贡献率较大。如果直接把所有风机的数据及其导数作为风电场功率预测模型的输入,其输入个数会非常巨大,因此基于上一节给出的NN-MIV方法,对输入变量进行筛选。

图1 风机分布图Fig.1 Distribution of wind turbines

首先,将46台风机的风速V、风向余弦Dcos及其1阶、2阶导数作为输入,风电场1 h的预测总功率PWP作为输出,构造一个结构为276-280-1的三层前向神经网络(如图2所示)。为获得较准确的导数信息,避免测量噪声对求导的影响,首先对测量数据进行平滑滤波,并用精度较高的七点求导公式对数据进行求导[20],以获得较高的精度,隐含层激励函数取为“tansig”函数,输出层激活函数选取“purelin”。用风电场30个典型工作日且未出现弃风情况的历史数据(采样间隔5 min,共8 640个样本),采用Levenberg-Marquardt训练算法对神经网络进行50次训练,使训练均方误差(MSE)小于0.001。

对训练好的神经网络,采用神经网络方法计算输入变量对输出变量的内部贡献率,采用平均影响值方法计算输入变量对输出变量的外部贡献率,最后计算出综合贡献率。

附录A表A1给出了各输入变量对预测功率输出的综合贡献率。由表A1可得出如下结论。

1)贡献率较大的变量主要是风机的风速V,但不是所有风机的风速对预测功率都有较大的贡献值,表明风速信息有一定的冗余,NN-MIV方法剔除了这些冗余信息。例如:12号风机位于11号、13号风机中间,其冗余信息已被11号、13号风机包含,因此12号风机的贡献率计算值很小。

图2 动态神经网络预测模型(由三层前向神经网络和微分器S构成)Fig.2 Dynamic neural network prediction model composed of 3-layer feedforward neural network and differentiators

2)大部分风机的风速导数对预测功率的贡献率不大,但也有部分风机的风速导数或2阶导数对输出有较大贡献,这些风机主要位于所有风机的外围,对风速的改变较为敏感,代表了整个风电场风速未来的变化趋势。

3)风向本身对预测输出贡献率非常小,但风向余弦的导数(主要是2阶导数)对预测功率有一定的贡献率,表明风向本身与功率输出基本无关,但风向余弦导数表示风向的变化,是一种能量转换的因素,与功率存在一定的关系,而风向余弦的二阶导数则对应着这种能量转换的未来变化趋势,因此对预测功率有相对大的贡献率。

4)贡献率较大的风机一般位于风电场的外围,能较快反映风速和风向的变化信息,与未来的风电功率有紧密的联系。但由于本文的贡献率计算方法是一种神经网络数据驱动的方法,因此贡献率的计算结果还与神经网络权值的随机初始化值密切相关。如果权值的初始化值导致某个(风机)节点数据权重较大,则该节点的贡献率会在神经网络训练中被强化,而权重较小的节点贡献率会被弱化,这可能导致地位相近的两个节点的贡献率差异较大的结果。当然这对最终的风电功率预测结果影响较小,因为贡献率小的变量,或者与风电预测功率联系不紧密,或者其信息已经被其他贡献率大的变量所包含。

根据变量选择原则,选择对预测功率贡献值最大的56个变量作为输入,使α为0.953 5,重新构造一个结构为56-60-1的神经网络预测模型,并采用与训练276-280-1神经网络相同的数据训练新的神经网络,然后对2个神经网络预测模型分别进行了风电功率预测的实验。预测实验采用训练样本集之后未出现弃风的某个典型工作日的数据(共288个预测点)。图3给出了不同方法预测的对比结果。

图3 静态神经网络模型、动态神经网络模型与NN-MIV模型的风电功率预测效果Fig.3 Wind power prediction results of static neural network, dynamic neural network and NN-MIV models

同时,本文还构造了一个输入为46台风机的风速和风向余弦,神经网络结构为92-100-1的静态神经网络预测模型。用训练动态神经网络和NN-MIV模型同样的数据训练静态神经网络模型,用检验动态神经网络和NN-MIV模型同样的数据检验静态神经网络模型的预测效果,其结果也在图3中给出。

为定量比较预测结果,表1给出了预测结果的均方根误差:

(16)

式中:Prated为风电场的额定容量;PWP,i为第i次预测风电功率;PW,i为第i次实测风电功率;n为预测数据个数。

为衡量在功率发生较大变化时的预测误差,表1给出了预测结果的最大相对误差指标(见式(17)),还给出了3种预测模型训练所需要的时间。

(17)

表1 3种预测方法结果比较Table 1 Result comparison between 3 prediction methods

从图3和表1可以看出:静态神经网络方法除了在训练时间上少于动态神经网络方法外,其他指标均比动态神经网络差;而NN-MIV方法不但具有最短的训练时间,最简单的结构,而且有最高的预测精度。以上结果可以说明:①动态神经网络预测方法通过引入导数,反映系统的动态特性,能够提高预测精度;②风电场风机的风速、风向及其各阶导数之中存在较多的对预测功率贡献较小或冗余的变量,通过NN-MIV方法能在保留95%以上有效信息的基础上大量减少这些贡献较小和冗余的变量,简化预测模型,降低引入测量噪声的概率,提高了模型的泛化能力和预测精度。

4 结语

基于动态神经网络的超短期风电功率预测方法由于采用变量的导数来表征系统的动态特性,使预测系统的输入中隐含了风速和风向未来的信息,能获得较好的预测效果。但对于风机数量多的大型风电场,直接使用该方法会导致神经网络结构复杂、训练时间长等问题。本文提出了一种基于NN-MIV的超短期风电功率预测方法,此方法将平均影响值和神经网络方法相结合,综合考虑了各输入变量对预测功率的外部贡献率和内部贡献率,筛选出了对输出变量贡献率最大的56个输入变量,建立了一个优化的神经网络超短期风电功率预测模型。实验结果表明,本文方法不仅能降低预测模型的复杂度,减少训练时间,而且能降低测量噪声对预测精度的影响,提高风电功率的预测精度。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

[1] SÖDER L, HOFMANN L, ORTHS A, et al. Experience from wind integration in some high penetration areas[J]. IEEE Trans on Energy Conversion, 2007, 22(1): 4-12.

[2] 何东,刘瑞叶.基于主成分分析的神经网络动态集成风功率超短期预测[J].电力系统保护与控制,2013,41(4):50-54.

HE Dong, LIU Ruiye. Ultra-short-term wind power prediction using ANN ensemble based on the principal components analysis[J]. Power System Protection and Control, 2013, 41(4): 50-54.

[3] 薛禹胜,郁琛,赵俊华,等.关于短期及超短期风电功率预测的评述[J].电力系统自动化,2015,39(6):141-151.DOI:10.7500/AEPS20141218003.

XUE Yusheng, YU Chen, ZHAO Junhua, et al. A review on short-term and ultra-short-term wind power prediction[J]. Automation of Electric Power Systems, 2015, 39(6): 141-151. DOI:10.7500/AEPS20141218003.

[4] JIANG Yu, CHEN Xingying, YU Kun, et al. Short-term wind power forecasting using hybrid method based on enhanced boosting algorithm[J]. Journal of Modern Power Systems and Clean Energy, 2017, 5(1): 126-133.

[5] COSTA A, CRESPO A, NAVARRO J, et al. A review on the young history of the wind power short-term prediction[J]. Renewable and Sustainable Energy Reviews, 2008, 12(6): 1725-1744.

[6] MU Gang, YANG Mao, WANG Dong, et al. Spatial dispersion of wind speeds and its influence on the forecasting error of wind power in a wind farm[J]. Journal of Modern Power Systems and Clean Energy, 2016, 4(2): 265-274.

[7] 陈颖,周海,王文鹏,等.风电场输出功率超短期预测结果分析与改进[J].电力系统自动化,2011,35(15):30-33.

CHEN Ying, ZHOU Hai, WANG Wenpeng, et al. Improvement of ultra-short-term forecast for wind power[J]. Automation of Electric Power Systems, 2011, 35(15): 30-33

[8] ALEXIADIS M C, DOKOPOULOS P S, SAHSAMANOGLOU H S, et al. Short-term forecasting of wind speed and related electrical power[J]. Solar Energy, 1998, 63(1): 61-68.

[9] BROWN B G, KATZ R W, MURPHY A H. Time-series models to simulate and forecast wind-speed and wind power[J]. Journal of Climate and Applied Meteorology, 1984, 23(8): 1184-1195.

[10] 郁琛,薛禹胜,文福拴,等.按时序特征优化模型后在线选配的超短期风电预测[J].电力系统自动化,2015,39(8):5-11.DOI:10.7500/AEPS20141230007.

YU Chen, XUE Yusheng, WEN Fushuan, et al. An ultra-short-term wind power prediction method using “offline classification and optimization, online model matching” based on time series features[J]. Automation of Electric Power Systems, 2015, 39(8): 5-11. DOI: 10.7500/AEPS20141230007.

[11] 李智,韩学山,韩力,等.地区电网风电场功率超短期预测方法[J].电力系统自动化,2010,34(7):90-94.

LI Zhi, HAN Xueshan, HAN Li, et al. An ultra-short-term wind power forecasting method in regional grids[J]. Automation of Electric Power Systems, 2010, 34(7): 90-94

[12] 刘爱国,薛云涛,胡江鹭.基于GA优化SVM的风电功率的超短期预测[J]. 电力系统保护与控制, 2015, 43(2): 90-95.

LIU Aiguo, XUE Yuntao, HU Jianglu, et al. Ultra-short-term wind power forecasting based on SVM optimized by GA[J]. Power System Protection and Control, 2015, 43(2): 90-95.

[13] 丁志勇,杨苹,杨曦,等.基于连续时间段聚类的支持向量机风电功率预测方法[J].电力系统自动化,2012,36(14):131-135.

DING Zhiyong, YANG Ping, YANG Xi, et al. Wind power prediction method based on sequential time clustering support vector machine[J]. Automation of Electric Power Systems, 2012, 36(14): 131-135.

[14] PRATHEEPRAJ E, ABRAHAM A, DEEPA S N. Very short term wind power forecasting using PSO-neural network hybrid system[J]. Advances in Computing and Communications, 2011, 192(3): 503-511.

[15] LI J, MAO J. Ultra-short-term wind power prediction using BP neural network[C]// 9th IEEE Conference on Industrial Electronics and Applications, June 9-11, 2014, Hangzhou, China: 2001-2006.

[16] 崔明建,孙元章,柯德平.基于原子稀疏分解和BP神经网络的风电功率爬坡事件预测[J].电力系统自动化,2014,38(12):6-11.DOI:10.7500/AEPS20130418003.

CUI Mingjian, SUN Yuanzhang, KE Deping. Wind power ramp events forecasting based on atomic sparse decomposition and BP neural networks[J]. Automation of Electric Power Systems, 2014, 38(12): 6-11. DOI: 10.7500/AEPS20130418003.

[17] 范高锋,王伟胜,刘纯,等.基于人工神经网络的风电功率预测[J].中国电机工程学报,2008,28(34):118-123.

FAN Gaofeng, WANG Weisheng, LIU Chun, et al. Wind power prediction based on artificial neural network[J]. Proceedings of the CSEE, 2008, 28(34): 118-123.

[18] 刘瑞叶,黄磊.基于动态神经网络的风电场输出功率预测[J].电力系统自动化,2012,36(11):19-22.

LIU Ruiye, HUANG Lei. Wind power forecasting based on dynamic neural networks[J]. Automation of Electric Power Systems, 2012, 36(11): 19-22.

[19] OZESMI S L, OZESMI U. An artificial neural network approach to spatial habitat modeling with interspecific interaction[J]. Ecological Modelling, 1999, 116(1): 15-31.

[20] 张腾.神经网络逆系统方法及其在电力系统控制中的应用[D].南京:东南大学,2002.

Ultra-short-termWindPowerPredictionBasedonNeuralNetworkandMeanImpactValue

XULongbo1,WANGWei2,3,ZHANGTao2,3,YANGLi1,WANGShaoyong1,LIYudong1

(1. Guangdong Electric Power Design Institute Co. Ltd., China Energy Engineering Group, Guangzhou 510663, China;2. NARI Group Corporation (State Grid Electric Power Research Institute), Nanjing 211106, China;3. NARI Nanjing Control System Co. Ltd., Nanjing 210061, China)

To solve the problems of variable redundancy and model complexity in the prediction model based on the dynamic neural network, an ultra-short-term wind power prediction method is proposed by combining the neural network (NN) and the mean impact value (MIV). In this method, the external and internal contribution rates of the input variables to the output variables (wind power prediction value) are taken into account, and the input variable with the largest contribution to the output variables is selected. Then an optimized NN prediction model for ultra-short-term wind power prediction is developed. The experimental results show that the proposed model reduces the complexity of the prediction model, mitigates the influence of the measuring noise on the prediction accuracy, and obtains good wind power prediction results.

This work is supported by National High Technology Research and Development Program of China (863 Program) (No. 2013AA050601).

wind power; ultra-short-term prediction; dynamic neural network (DNN); mean impact value (MIV); variable selection

2017-03-21;

2017-07-20。

上网日期: 2017-09-19。

国家高技术研究发展计划(863计划)资助项目(2013AA050601)。

徐龙博(1984—),男,硕士,高级工程师,主要研究方向:新能源发电。E-mail： xlbsjtu@163.com

王 伟(1967—),男,通信作者,硕士,高级工程师,主要研究方向:新能源发电监视与控制。E-mail: wangwei2@sgepri.sgcc.com.cn

张 滔(1982—),男,硕士,工程师,主要研究方向:新能源发电监视与控制。E-mail: zhangtao6@sgepri.sgcc.com.cn

(编辑蔡静雯)