工期约束下加工型产品准确率串归约算法研究

罗智勇，汪 鹏，尤 波，苏 洁



工期约束下加工型产品准确率串归约算法研究

罗智勇1,2，汪 鹏1，尤 波2，苏 洁1

(1. 哈尔滨理工大学计算机科学与技术学院 哈尔滨 150080；2. 哈尔滨理工大学机械动力工程学院 哈尔滨 150080)

完工时间和准确率是生产调度的两个重要属性，然而单属性优化算法只能完成单个属性的优化，无法动态平衡这些属性。针对此问题，提出了基于有向无环图的串归约优化算法。算法通过约束每个任务的活动区间并采用逆向迭代进行归约，达到每层选择最优服务的目的，从而实现了这两个属性的优化。实验表明，该算法可准确地得到一条完工时间和准确率相互平衡的优化路径，但其优化效率受限于完工截止期和任务数。最后，研究结论对生产调度多属性的优化提供了一定的参考。

准确率优化; 截止期; 时间一致性; 工作流调度

现代业务的工作流技术是在网络流的基础上以服务为基本元素进行架构，使多个服务相互协作来完成整个业务。工作流系统将业务流程抽象化，划分为诸多工序，并结合工序中的服务属性，确定最佳完工路径。然而，目前企业的项目流程，往往因为一个或者几个工序出现问题而影响整体，如追求效率而忽略了服务质量或者追求服务质量而拖延了完工时间，使得整个项目的完工时间和完工质量失衡。为此，应该使用更合理的方法，在业务流程规定的截止期内，选择一条能够有效提升复杂项目准确率的路径，达到既能充分利用资源，又能使效率和准确率实现平衡的目的[1]。

本文提出了一种加工型产品工作流在限定完工时间内，保证工序完工质量最高的算法，即实现了完工路径质量的串归约优化。

1 相关工作

工作流模型包含任务和服务两大要点，服务在工作流模型中承载着时间、费用和服务质量等属性，合理搭配服务之间的联系对优化任务的顺利进行起着关键性作用[2-3]。随着工作流结构的不断拓展，工作流的优化不再以时间为根本，而是对其完工时间和完工质量有了更高的要求。文献[4]结合时间启发函数和遗传算法的优点，提出一种混合式算法，通过实验证明了该策略的优化效果；文献[5]针对资源配置可能存在的不确定性弊端，提出了一种截止驱动调度算法，有效地降低了成本并保证了完工时间；文献[6]在混合式工作流的基础上提出了类似VM的并行任务处理方案，有效地降低了执行成本；文献[7]利用任务在进程中的灵活性并结合工作流的健壮性，提出了一种任务动态重排的方法，能够有效降低前驱任务对后续任务的影响，以达到资源合理分配的目标。

基于在约束时间下降低成本的问题，国内也开展了相应的研究。文献[8-9]都是在混合式复杂工作流上约束时间进而优化成本，分别利用逆向分层策略和串归约策略对每个活动结点划分活动区间，以局部选择最优服务来达到全局的优化。文献[10]采用优先级因子技术来优化复杂工作流的时间和成本的算法，并对不同的算法进行了比较分析。文献[11]对粒子进行初始化并进行了筛选，在此基础上提出了基于粒子群算法的优化调度策略，同时减少搜索时间。可见，现代工作流技术大部分追求的是时间和成本的平衡，而在约束时间下有效优化准确率也是一个研究热点。

2 问题描述

2.1 工作流模型的相关定义

工作流建模是对业务过程的一个合理安排，能够有效地将服务安排到对应任务的服务集合中[12]，并将加工型产品生产工序组成一个有向无环图。

定义1 任务池。是指在给定业务的流程中，将所有任务构成一个集合，若用表示，则=(1,2,…,p,…,p)。

定义2 服务池。指对于任务集合中的任意一个任务p，所对应的所有服务构成的集合。用S=(1,2,…,s,…,s)表示。

定义3 服务池的秩。指对于任务集合中的任意一个任务，其服务集合S中服务的数目，用r表示。

定义4 工作流图。即是网格环境下的有向无环图DAG与任务池、服务池相结合用来清楚描述业务流程的图，表示为={s,}，∈，0<≤r。其中，s表示任务用服务集合S中的第个服务完成；为有向边，表示每层的服务之间存在着顺序关系。工作流图中，没有前驱的结点为开始结点，记为结点Start，用p表示虚拟的任务，S表示虚拟的服务集合，并指向Start结点；没有后继的结点为完成结点End，用p表示虚拟的任务，用S表示虚拟的服务集合，并指向End结点。

定义5 服务属性。是指工作流图中服务s带有的属性参数，表示为pt=(t,a)，t表示使用服务池S中的第个服务完成任务的时间，a表示达到的准确率。

2.2 约束定义

定义6 完工时间。指产品的生产从开始到结束耗费的时间，记为。

定义7 完工准确率。指产品的生产从开始到结束达到的准确率，记为。

定义8 截止期。指产品的生产约束限定时间，记为。

对于建立的工作模型，此时需要有规定的约束策略，对流程的形式化为：

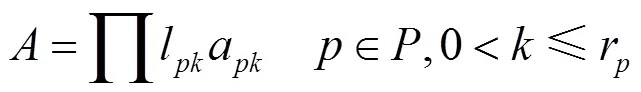
即表示一条能够完成加工型产品路径的准确率。当执行一个任务时，只能选择一个服务来完成该任务，即：

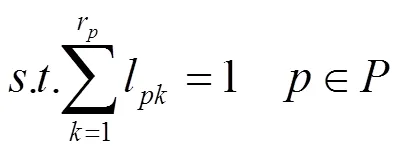
完成加工型产品所用的时间必须低于或等于截止时间，即；

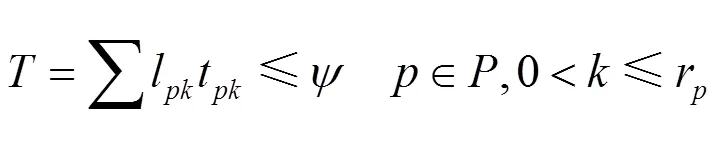
式中，l是一个变量，即：

在截止期下，以式(1)为启发目标函数，在式(2)～式(4)的约束条件下，求得能够完成加工型产品路径的准确率，此时采用不同的算法策略求得对应路径的准确率。

3 传统单向目标算法

一个加工型产品的生产工序，承载着完工时间和完工准确率的属性，传统单向目标的算法策略是指在生产过程中，仅仅保证了完工时间最小或者仅保证了完工准确率最大。

3.1 最小时间的单向目标优化算法(TMG)

选择每个工序完成时间最小的服务组成工作序列，即：

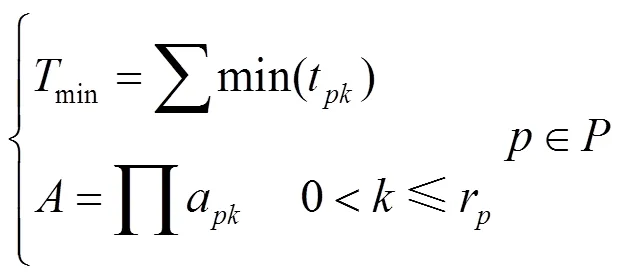
式中，min为限定条件，即时间最小化；在限定条件min下可求得完工准确率。

3.2 最大准确率的单向目标优化算法(AMG)

选择每个工序完成准确率最大的服务组成工作序列，即：

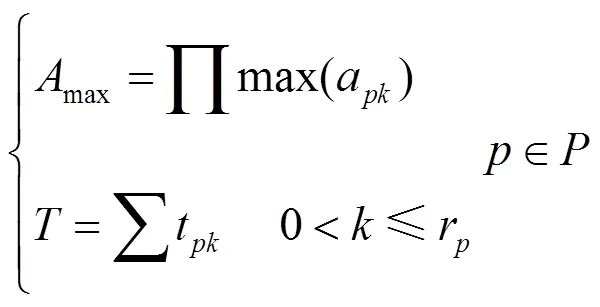
式中，max为限定条件，即达到完工准确率最大化；在限定条件max下可求得完工时间。

4 基于串归约的时间-准确率优化策略

4.1 相关定义

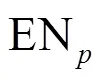
4.2 算法描述

串归约优化算法是在每层任务的活动区间内选择合适的服务，实现复杂产品的完工时间和准确率平衡的目标。由于在活动区间内的服务存在不能充分利用时间的问题，因此会产生一些时间碎片。串归约算法充分利用在截止期范围内的时间，把时间碎片集中起来，产生一个局部最优解。本文以任务的自由度为基础，对于任务集合中的每个任务，都有一个WF=[ST,EN]，采用动态规划的方式，以后继活动不同时间点开始时达到的局部最优解求得当前活动不同时间点开始时达到的最优解，通过比较完工的准确率确定最佳路径。

针对含有个任务的工作流图，用()表示工作流图中的第个任务在时间开始时达到的最大准确率，其中∈[ST,EN]。以最后一个活动为起点，迭代求出前驱活动相应的值，最后一个活动的由式(8)求得：

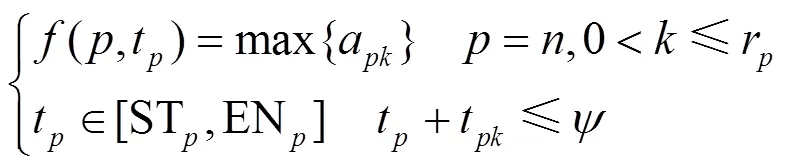
对已经求解每个活动自由度的业务流程，以活动的相关值(p,t)，求解前驱活动¢对应的(¢,t¢)，该迭代过程由式(9)求得：

通过层层迭代，当遍历到初始任务时，最大准确率的服务组合即为业务流程最佳路径。

基于串归约的时间-准确率优化算法SRO伪代码如下：

Input：,S

Output：最佳路径。

Val=.length();

For(int=1;≤;++) {

Figure WFby Formula (7));}

Figure(,) by Formula (8);

For(=-1;>0;--){

Figure(,) by Formula (9)};

if(=1){

Search max((,));}

经分析：SRO算法对应的时间复杂度为(m)。

5 案例分析

5.1 案例设计

组装工艺的一般过程分为备料、形成坯件、零部件加工、部件组合、总组合和表面涂饰6个环节，存在虚拟的开始任务和结束任务，分别为申请和竣工，则该业务流程可抽象化表示1,2,3,4,5,6,s,p。此时每个环节对应一个服务池S，对应的服务带有一定的属性参数，数据如表1所示。

表1 服务时间及准确率

5.2 算法分析

由以上的任务和服务列表，建立如图1所示的工作流图。

基于图1的工作流图，规定本业务流程的截止期=21，采用本文的传统单向目标算法和基于串归约的时间-准确率优化算法进行计算。

5.2.1 传统单向目标算法策略

1) TMG算法。调用式(5)求得对应的工作流程为11->21->31->41->51->61，此时对应的限定条件min=11+21+31+41+51+61=16，则可求得对应工作流程的准确率=112131415161=0.727;

2) AMG算法。调用式(6)求得对应的工作流程为13->22->33->42->53->62，此时对应的限定条件max=132233425362=0.859，则对应工作流程的完工时间=13+22+33+42+53+62=31。

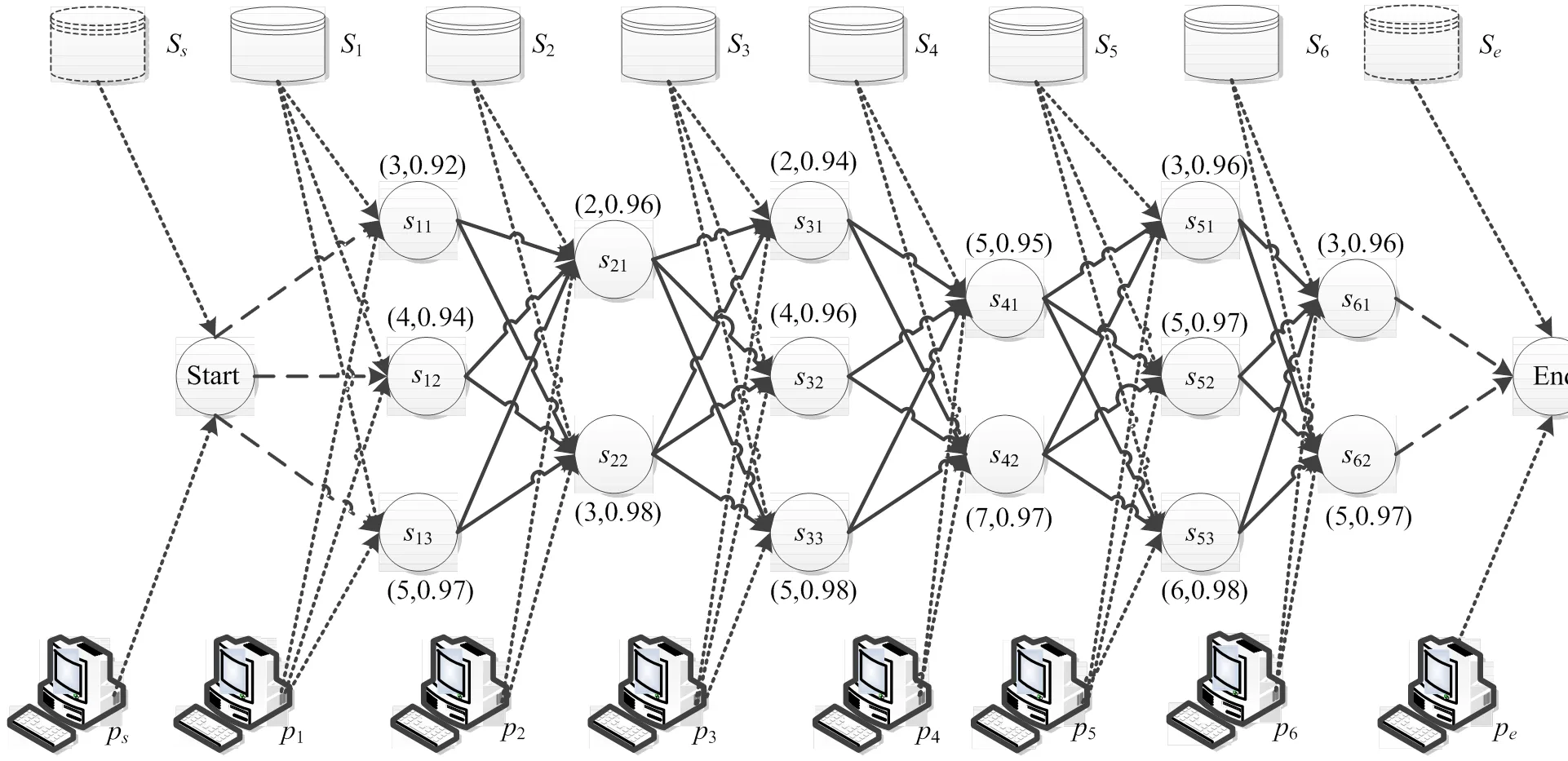
图1 工作流图

5.2.2 SRO算法

结合业务流程的任务及其对应的服务属性，调用算法SRO可得：任务1自由度为[0,3]，任务2自由度为[3,6]，任务3自由度为[5,8]，任务4自由度为[7,10]，任务5自由度为[12,15]，任务6自由度为[15,18]，并可求出各个任务在相应的任务自由度内，不同时间开始执行取得的最大准确率，其计算过程及结果如表2所示：

表2 计算结果

由(1,0)=0.783可知，此时的完工准确率最大，则可明确基于串归约算法的最佳路径为：任务1从0时开始，用对应的13服务，所用时间为5；任务2从5时开始，用对应的22服务，所用时间为3；任务3从8时开始，用对应的31服务，所用时间为2；任务4从10时开始，用对应的41服务，所用时间为5；任务5从15时开始，用对应的51服务，所用时间为3；任务6从18时开始，用对应的61服务，所用时间为3。

5.3 算法比较

结合上述不同算法求得的完工结果，可求出每种算法在不同时刻达到的准确率及所用时间，如图2a所示；并能得到不同的完工路径，如图2b所示。

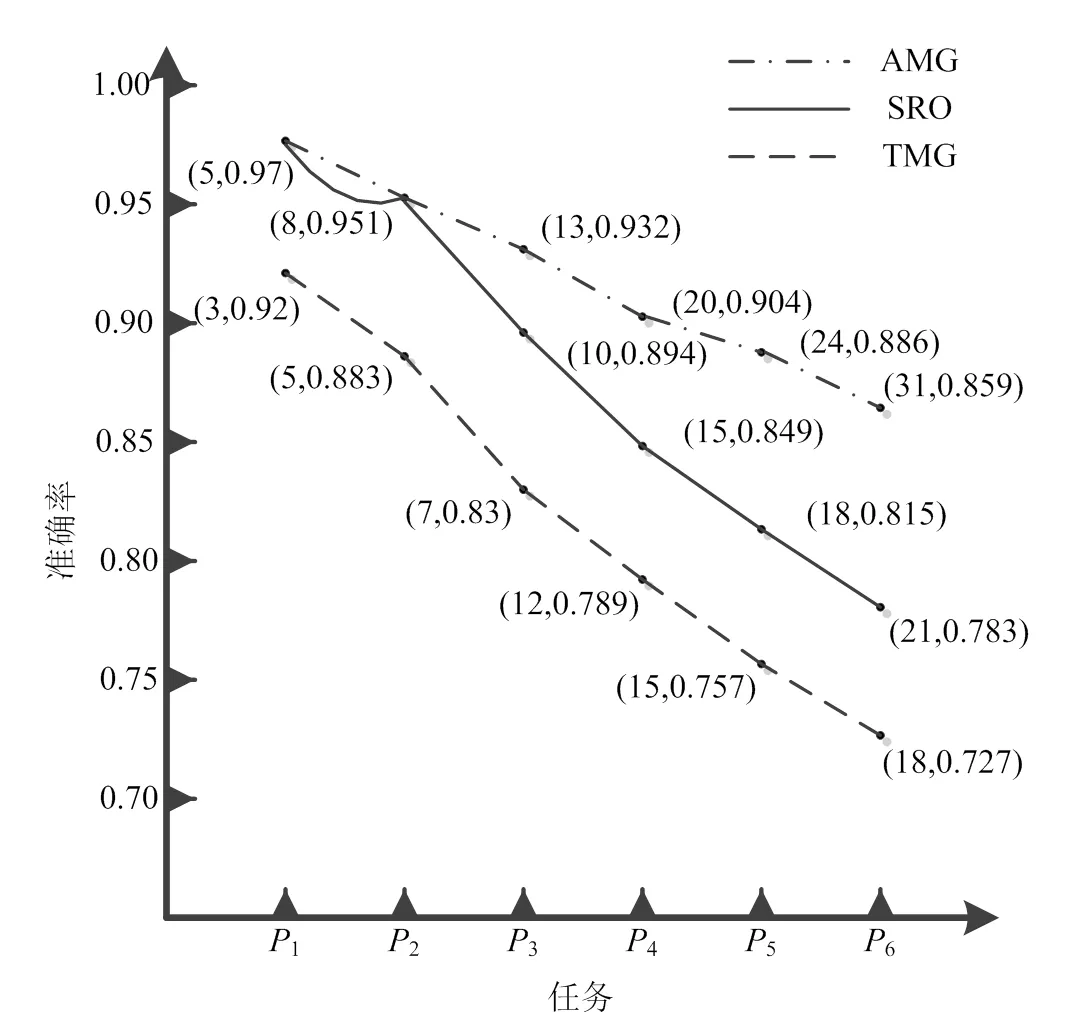
a. 不同任务时刻的准确率及所用时间

b. 不同算法对应路径

图2 不同算法的对比

从图2a中可知，对应业务进行到任务6时的准确率即完工准确率，此时可看出AMG算法的完工准确率最大，但由于出现完工时间高于截止期的情况，因此该策略不能被执行。TMG算法和SRO算法的完工时间满足约束条件，因此利用完工准确率10.783、20.727，可计算SRO算法相对于TMG算法的优化率=7.7%。因此，SRO算法具有一定优化调度优势。图2b可知，SRO算法从开始到完成，其服务选择为13->22->31->41->51->61。

6 其他参数对算法性能的影响

6.1 截止期ψ大小产生的影响

截止期是工作流的最晚完工时间，随着截止期的增大，业务流程的总体准确率也会得到优化。本文采用的基于串归约的时间-准确率优化算法主要是建立在时间约束的基础上，因此通过增大截止期，某些任务的自由度也会变大，可以选择更佳的服务来执行。实验选择任务数为10和15的业务流图，并以区间[2,4]的随机值作为服务池大小，每个任务具有服务及其对应的属性等特性。以min作为每个业务流图的最小完工时间，并在此基础上增加10%、15%、20%、25%、30%作为业务流图的不同截止期，业务流图在不同截止期下达到的最大完工准确率如图3所示：

通过图3可得出，当截止期为min时，即基于时间最小化策略。不同的业务流程，随着截止时间的增大，相对于以时间最小化为目标的算法，串归约优化算法的准确率越来越大，算法性能得到了优化。因此，在实际的业务过程中，可适当用大点截止期，串归约算法的优化作用将会越来越明显。

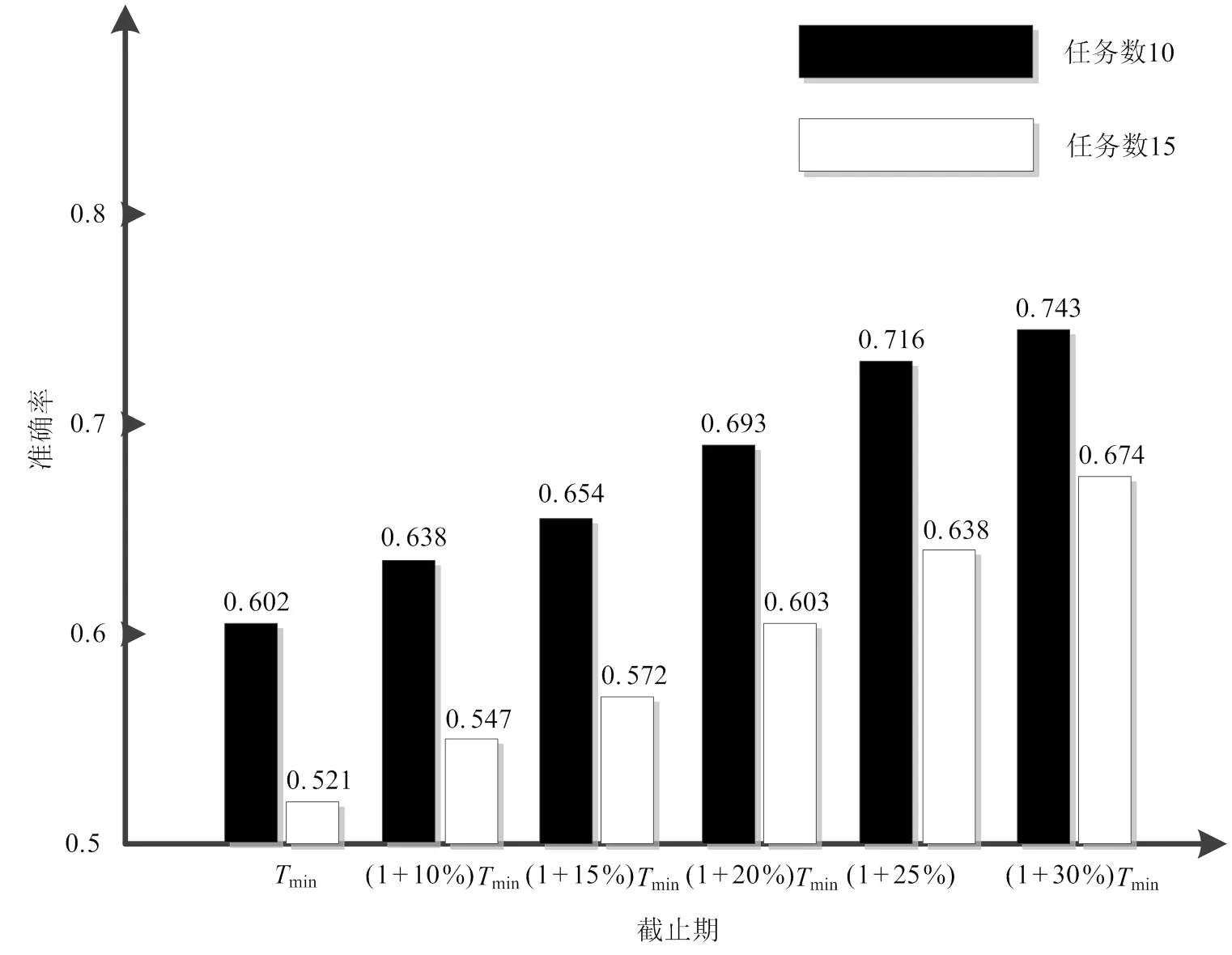
图3 不同截止期ψ对算法性能的影响

6.2 任务的数目对性能的影响

工作流中的某条路径的准确率是通过该路径上所有服务准确率的乘积而来，随着任务数目的增多，对整体的完工准确率及SRO算法的优化效果均会产生不同的影响。实验选择集合{5,10,15,20}中的值为任务数，并以区间[2,4]的随机值作为服务池大小，每个任务具有服务及其对应的属性等特性，生成不同的业务流图。以min作为每个业务流图的最小完工时间，并在此基础上增加20%作为不同流图的截止期，不同业务流图在不同算法策略下达到的完工准确率如图4所示。

图4 任务数目对算法性能的影响

从图4的数据可以得出，随着任务数目的增多，每个环节都存在着偏差，总体的完工准确率会随着降低，但串归约优化算法的优化效果更加明显，算法提高率分别为7.26%、11.4%、16.8%、25.2%。

7 结束语

针对工作流截止期约束下的准确率优化问题，本文采用了任务、服务与有向无环图DAG相结合的方式，生成工作流模型。在此基础上，提出了在截止期约束下的串归约优化算法，通过对工序的每个环节进行时间约束，以逆向迭代的方式，求得每层任务在不同时刻开始时的最大准确率，所有任务都完成时以最大完工准确率确定优化路径。实验数据表明，相比于传统的单向目标算法，串归约优化算法的优化率达到了7.7%。与此同时，本文还对影响优化效果的因素即截止期的范围和业务流程的任务量进行了分析。但还存在没能将业务流程的运作成本考虑进去的问题，在此还需要进一步研究讨论，充分考虑在业务流程中服务的相关属性，真正找出一条具有效率化、准确化并能充分降低成本费用的最佳路径，以后的研究会进一步地改进并加以完善。

[1] DE P, DUNNE E J, GHOSH J B, et al. Complexity of the discrete time-cost tradeoff problem for project networks[J]. Operations Research, 1997, 45(2): 302-306.

[2] BUYYA R, GIDDY J, ABRAMSON D. An evaluation of economy-based resource trading and scheduling on computational power grids for parameter sweep applications[C]//Active Middleware Services. [S.l.]: Springer, 2000: 221-230.

[3] BUYYA R, ABRAMSON D, JONAT H G, et al. Economic models for resource management and scheduling in grid computing[J]. Concurrency & Computation: Practice & Experience, 2002, 14(13-15): 1507-1542.

[4] NASONOV D, VISHERATIN A, BUTAKOV N, et al. Hybrid evolutionary workflow scheduling algorithm for dynamic heterogeneous distributed computational environment[J]. Journal of Applied Logic, 2016, 299: 83-92.

[5] MA Z, CAO J, QIAN S. DDS: a deadline driven workflow scheduling algorithm for hybrid amazon instances[M]. [S.l.]: Advances in Services Computing, 2015.

[6] YOON D, KIM S H, KANG D K, et al. Hybrid workflow management in cloud broker system[C]//Cloud Computing. [S.l.]: Springer, 2015: 145-155.

[7]CHEN W, LEE Y C, FEKETE A, et al. Adaptive multiple- workflow scheduling with task rearrangement[J]. Journal of Supercomputing, 2015, 71(4): 1297-1317.

[8] 苑迎春, 李小平, 王茜, 等. 基于逆向分层的网格工作流调度算法[J]. 计算机学报, 2008, 31(2): 282-290.

YUAN Yin-chun, LI Xiao-ping, WANG Qian, et al. Bottom level based heuristic for workflow scheduling in grids[J]. Chinese Journal of Computers, 2008, 31(2): 282-290.

[9] 苑迎春, 李小平, 王茜. 基于串归约的网格工作流费用优化方法[J]. 计算机研究与发展, 2008, 45(2): 246-253.

YUAN Yin-chun, LI Xiao-ping, WANG Qian. Cost optimization heuristics for grid workflows scheduling based on serial reduction[J]. Journal of Computer Research and Development, 2008, 45(2): 246-253.

[10] 刘灿灿, 张卫民, 骆志刚. 基于逆向分层的工作流时间-费用优化方法[J]. 国防科技大学学报, 2013, 35(3): 61- 66.

LIU Can-can, ZHANG Wei-min, LUO Zhi-gang. Time and cost trade-off heuristics for workflow scheduling based on bottom level[J]. Journal of National University of Defense Technology, 2013, 35(3): 61-66.

[11] 曹斌, 王小统, 熊丽荣, 等. 时间约束云工作流调度的粒子群搜索方法[J]. 计算机集成制造系统, 2016, 22(2): 372- 380.

CAO Bin, WANG Xiao-tong, XIONG Li-rong, et al. Searching method for particle swarm optimization of cloud workflow scheduling with time constraint[J]. Computer Integrated Manufacturing Systems, 2016, 22(2): 372-380.

[12] 武星, 卓少剑, 张武. 成本最优化工作流技术驱动的研发协同软件即服务应用[J]. 计算机集成制造系统, 2013, 19(8): 1748-1754.

WU Xing, ZHUO Shao-jian, ZHANG Wu. Cost optimization workflow-driven SssS for collaborative research and development[J]. Computer Integrated Manufacturing Systems, 2013, 19(8): 1748-1754.

编 辑 蒋 晓

Research on Serial Reduction Algorithm for Accuracy of Processing Products under Time Constraints

LUO Zhi-yong1,2, WANG Peng1, YOU Bo2, and SU Jie1

(1. School of Computer Science and Technology, Harbin University of Science and Technology Harbin 150080; 2. School of Mechanical Engineering, Harbin University of Science and Technology Harbin 150080)

Completion time and accuracy are the most important attributes of processing products’ business, however, single attribute optimization algorithm only can optimize one attribute, let alone balancing these two attributes dynamically. In order to fix this problem, a serial reduction algorithm based on directed acyclic graph is proposed. The algorithm constraints each tasks' activity section by using backwards iterative eduction to choose appropriate service for achieving the optimization of these two attributes. Statistical data shows that serial reduction algorithm does get an optimized path with time and accuracy balance, but its optimization efficiency is limited by the completion deadline and the number of tasks. The research conclusion provides a certain theoretical reference for the optimization of production scheduling.

accuracy optimization; deadline; temporal consistency; workflow schedule

TP393

A

10.3969/j.issn.1001-0548.2017.06.022

2016-06-20；

2016-12-22

国家自然科学基金青年项目(61403109)

罗智勇(1978-)，男，副教授，主要从事网络安全、科学工作流调度方面的研究.