基于PNGV模型和高斯-厄米特滤波的SOC估算研究
2017-12-22凡旭国周金治
凡旭国,周金治,2
(1.西南科技大学信息工程学院,四川 绵阳 621010;2.特殊环境机器人技术四川省重点试验室,四川 绵阳 621010)
基于PNGV模型和高斯-厄米特滤波的SOC估算研究
凡旭国1,周金治1,2
(1.西南科技大学信息工程学院,四川 绵阳 621010;2.特殊环境机器人技术四川省重点试验室,四川 绵阳 621010)
为解决锂离子电池荷电状态(SOC)估算精度不高和初值鲁棒性差的问题,提出了一种基于新一代汽车伙伴计划(PNGV)等效电路模型和高斯-厄米特滤波(GHF)算法的锂离子电池SOC估算方法。首先,建立PNGV模型来模拟电池的动静态工作特性,列出该等效电路模型的状态空间方程;然后,利用混合动力脉冲能力特性测试试验,对模型中的动态参数进行辨识,并通过电流激励下的电压响应对比验证了模型及参数的有效性;最后,结合GHF算法得出了算法的系数矩阵和递推过程。在Matlab/Simulink平台上,对该SOC估算方法的估算效果进行了仿真分析与验证。结果表明,无论是在恒流、周期恒定电流和周期变电流工况下,还是在城市道路循环(UDDS)变电流工况下,SOC都能实时跟踪真实值的变化。同时,该算法对初值有较好的鲁棒性。在初始SOC为0.8的情况下,SOC估算最大误差不超过3.7%,具有较高的精度。该算法为锂离子电池SOC的估算提供了一种新的思路。
锂离子电池; 电池管理系统; 等效电路; 高斯-厄米特滤波; 荷电状态; 参数辨识; 混合脉冲能力特性
0 引言
锂离子电池荷电状态(state of charge,SOC)的估算是电池管理系统(battery management system,BMS)的关键技术之一。准确的电池状态估计可以使电池得到充分、合理的利用,从而达到延长电池使用寿命的目的[1]。对于SOC的估算,工程上较多采用安时积分法。其主要思想是将动力电池作为一个黑箱,电池的输入、输出电量可以利用充放电电流在时间上的积分进行计算。但是,该方法的缺点是存在累计误差,并且对算法初值的要求较高。
为解决该问题,Plett[2]在建立电池模型的基础上,将扩展卡尔曼滤波(extended Kalman filter,EKF)算法应用于SOC估算。但EKF算法要求非线性方程一阶可微,并且较依赖系统的非线性程度,对于动力电池这种具有高度非线性的系统很可能达不到收敛的效果。Plett后来又提出了无迹卡尔曼滤波(unscented Kalman filter,UKF)算法,用来解决SOC估算过程中的非线性问题。该算法主要采用无迹变换,而非传统的线性化处理方法,从而消除了线性化处理过程中的系统误差,提高了预测精度[3]。
高斯-厄米特滤波(Gauss-Hermite filter,GHF)算法在处理非线性、非高斯问题上有很大优势,并且被广泛应用在目标跟踪、最优估计等领域。文献[4]针对传统粒子概率假设密度滤波估计精度不高且容易发散的问题,将高斯-厄米特粒子滤波算法运用在目标跟踪中,在有效解决观测方程非线性问题的同时,也提高了跟踪精度。文献[5]在高斯-厄米特滤波的过程中引入了自适应因子,通过适当调整高斯-厄米特滤波过程中的增益,自适应地调节滤波的均值与方差,进一步提高了滤波精度。文献[6]将高斯-厄米特滤波算法应用在SOC估算领域。其将GHF与二阶RC等效电路模型相结合,对电池SOC进行实时估算,取得了一定的估算效果,并将最终结果与UKF估算结果进行比对,验证了高斯-厄米特滤波算法的优越性。但是,该算法的精确度以及抑制系统噪声的能力有待进一步提高。
本文提出了一种基于新一代汽车伙伴计划(partner for a new generation of vehicles,PNGV)等效电路模型和高斯-厄米特算法的锂离子电池SOC估算方法。首先,建立PNGV模型的状态空间方程;然后,对模型的参数进行辨识,将GHF算法与PNGV模型相结合推导出算法系数矩阵;最后,在Matlab/Simulink平台上对该方法进行仿真分析,并给出了仿真效果。
1 锂离子电池等效电路模型
锂离子电池在使用过程中会对外呈现出极化和滞后的效应。该效应与电路阻容模型所表现出的特性一致[7],所以可以对电池进行等效电路建模。等效电路建模通常是指利用基本电路元器件构成一定的电路网络,来描述电池的工作特性。PNGV是一种较为常用的电池等效电路模型。
1.1 PNGV等效电路模型
PNGV模型是2001年《PNGV电池试验手册》中的标准电池模型[8],其等效电路模型如图1所示。该模型可以用来描述电池的工作特性。该模型中,OCV为电池的开路电压,R0为电池的欧姆内阻,RP为电池的极化内阻(由浓差产生),Cp为极化电容,IP(t)为流过极化内阻的电流,Cb为负载电流累计产生的开路电压的变化。
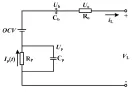
图1 PNGV等效电路模型
1.2 模型状态方程的建立
电池SOC是其内部的一个状态量,不能直接通过测量得到,它是一个与所采用估计方法有关的值。在对SOC进行估算时,通常在电池等效模型状态方程的基础上,把电池看作一个系统。将电池的充放电电流视为系统的输入、电池端电压视为系统的输出,并将电池SOC和一些模型参量作为系统需要估计的状态量。
因此,根据基尔霍夫电压电流定理,并以图1的PNGV模型中的2个电容电压UP、Ub和SOC为状态量,建立模型的状态空间方程,具体如式(1)、式(2)所示。
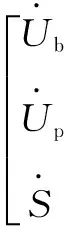
(1)
(2)
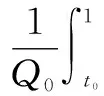
通过测量在t0到t时刻流过电池的电流I1,可以计算出该段时间内电流的积分,并用充电率或放电率η对这个积分进行加权,得出SOC。
将式(1)和式(2)经过离散化处理后,得到式(3)、式(4)所示的状态空间方程:
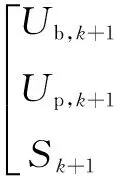
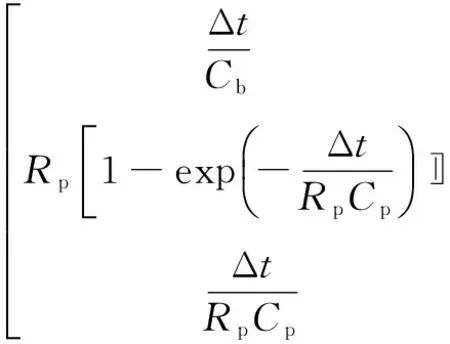
(3)
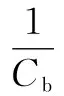
(4)
式中:f(Sk)为SOC与开路电压的关系函数;ω1、ω2、ω3为系统噪声;vk为观测噪声。
1.3 模型参数辨识
电池模型的参数是进行SOC估算的重要数据。在电池的工作过程中,其参数一般不是固定值。因此,在确立等效电路模型后,必须采用一定的方法来辨识出电路中的各个参数。
参数辨识是在模型结构已知的情况下,利用已知试验样本数据来求解模型未知参数的数学方法。本文模型参数辨识采用《FreedomCAR 电池试验手册》[9]中的混合脉冲能力特性(hybrid pulse power characteristic,HPPC)试验。它是一种用来体现动力电池脉冲充、放电特征的试验。在HPPC放电、静置以及充电的单循环试验中,采集电池单体的电压,得出其电压特性曲线;参考该电压响应曲线,可以获取电池模型的欧姆内阻参数和极化效应参数。
在整个HPPC试验中,采用1.3 A(即0.5 C)的电流在间隔为10%的SOC进行恒流放电,使SOC从100%等间隔下降至0。相邻脉冲试验之间电池搁置1 h,每个静置期间,分别进行10 s的放电、40 s的静置和10 s的充电。
当SOC=0.9时,HPPC测试的电压响应曲线如图2所示。

图2 HPPC测试的电压响应曲线(SOC=0.9)
根据每个SOC点的电压、电流数据,利用Matlab内置的lsqcurvefit非线性最小二乘函数接口,辨识PNGV模型中的各个动态参数。
根据混合脉冲功率性能测试,得到各SOC阶段模型的参数如表1所示。
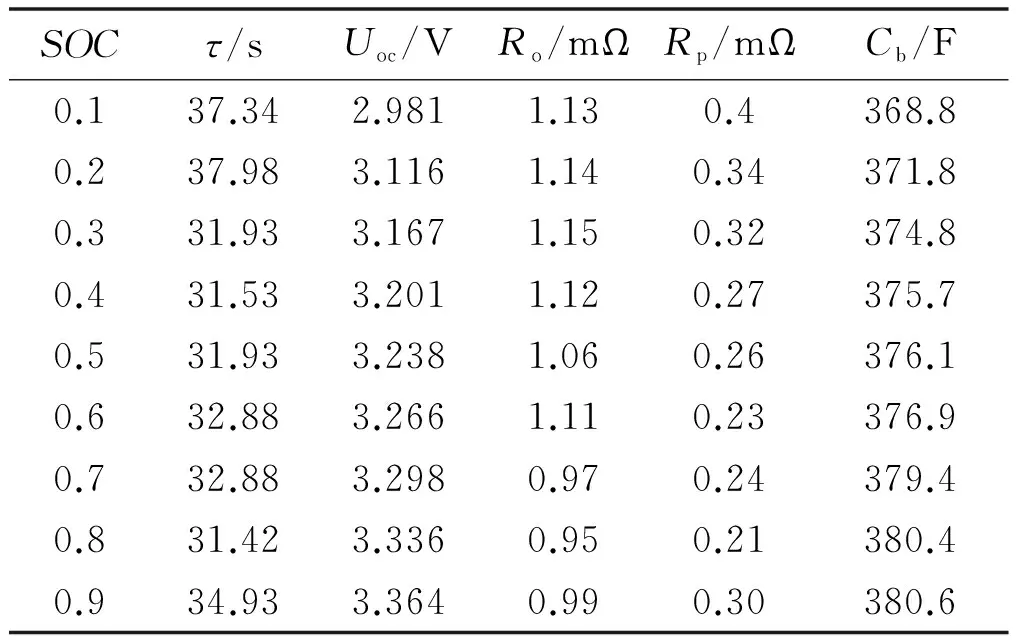
表1 各SOC阶段模型参数表
1.4 模型及参数有效性验证
电池等效电路模型及辨识出的参数需要进行有效性验证。对此,可以通过对比电流激励下的电压仿真输出与实际试验中电池的电压输出,来判断电池模型和参数的性能。
在试验室平台下,对标称容量为2.6 Ah的锂离子电池单体在室温(25 ℃)下进行充放电试验,以试验数据为基础进行Matlab仿真分析,并与实际结果进行了比较。一组自定义充放电的仿真电压和真实电压波形对比如图3所示。

图3 仿真电压波形与真实电压波形对比图
由图3可以看出,模型端电压输出与实际端电压吻合较好,说明PNGV模型能较好地模拟电池的动静态工作特性。
2 高斯-厄米特滤波算法
高斯-厄米特滤波是一种递归的贝叶斯滤波算法。该算法主要利用高斯-厄米特数值积分,选择高斯点以及相应的权值,进而提高系统状态均值及方差估计的代数精度[10]。
2.1 非线性问题描述
考虑如下非线性的状态空间模型[11]:
(5)
式中:f(xk-1)为系统在(k-1)时刻的状态函数;h(xk)为系统在k时刻的观测函数;xk为k时刻状态向量的估计值;yk为k时刻系统的观测值;ωk和vk分别为系统噪声和观测噪声。vk和ωk满足以下关系式:
(6)
式中:Qk和Rk分别为系统噪声方差阵和测量噪声方差阵。
2.2 高斯-厄米特滤波
假设上述非线性系统的概率密度函数服从高斯分布,那么可以在高斯滤波框架下,运用如式(7)所示的高斯-厄米特积分公式得到系统的状态预测和测量更新方程[12]。
(7)
在(k-1)时刻,设系统状态及其方差的估计分别为xk-1|k-1和Pk-1|k-1。由高斯点变换公式xi=STqi+xk-1|k-1和Pk-1|k-1=STS,可得系统状态及方差的一步预测为:
(8)
(9)
xk|k=xk|k-1+Lk(yk-zk)
(10)
(11)
其中:
Lk=Pxz(Rk+Pzz)-1
(12)
(13)
(14)

(15)
3 SOC估算仿真分析和验证
在已建立PNGV等效电路模型的前提下,使用高斯-厄米特滤波对电池的SOC进行实时估计。在Matlab/Simulink平台上搭建SOC估算仿真模型,将试验测试的数据转换为Matlab软件的.mat数据输入模型中,并设置仿真时间。采样间隔取1 s,经过模型的递推估算,可实时在线得出每一时刻SOC的最优估计值。为了验证高斯-厄米特滤波算法在实际估算过程中的效果,本文设定了用于模拟电池的多种实际工况,以验证算法对SOC估算的优越性和有效性;同时,对该算法的收敛性及误差进行了分析。
3.1 恒流放电时电池SOC估算及分析
在恒流放电试验中,首先将电池充电至SOC=1,然后分别采用1.3 A(0.5 C)和2.6 A(1 C)恒流放电。当电池的输出电压降至截止电压时,可认为电池的SOC=0。图4为电池分别在1.3 A(0.5 C)和2.6 A(1 C)恒流放电下,高斯-厄米特滤波算法根据电池实际的电压和电流,并结合所建立的电池模型,对电池SOC进行估算的结果。
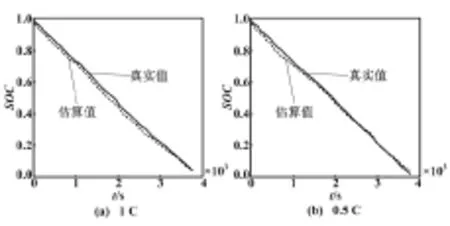
图4 SOC估算值与真实值对比曲线
从图4可以看出,在整个恒流放电的情况下,利用高斯-厄米特滤波算法估计的SOC值,能够实时跟踪真实SOC值的变化,算法的修正效果较好。
3.2 周期放电时电池SOC估算及分析
锂离子电池有时会在周期性放电工况下工作。为了验证高斯-厄米特滤波算法在此类工况下对SOC的估算精度,对锂离子电池进行了周期放电试验。根据试验得到的电池电流和电压数据,结合前文辨识出的模型各个动态参数,利用高斯-厄米特算法得到每一时刻SOC的最优估算,同时把得到的结果与真实值比较。恒流放电和变电流放电时,电池SOC估算及分析如图5所示。
由图5可知,通过对比锂离子电池在两种工况下的SOC估算值,可以看到电池试验数据经过高斯-厄米特滤波后,估算值与真实值比较接近。当电池的SOC在0.3以上时,预测精度较高;当SOC下降到0.3以下时,基于电路模型的高斯-厄米特滤波会出现一定的估算误差,这是由于放电末端电池内阻变化剧烈所造成的。

图5 SOC估算及分析曲线(周期放电)
3.3 剧烈电流时电池SOC估算及分析
为了验证GHF算法在剧烈电流变化条件下对SOC的估算效果,试验使用ADVISOR[13]软件中的城市道路循环(urban dynamometer driving schedule,UDDS)工况测试锂离子电池。将锂离子电池SOC初值定为1,按照UDDS测试功率要求,进行1次循环放电,循环放电时间为1 370 s、采样频率为1 Hz,并实时记录锂离子电池电压、电流和SOC等工作数据。
分别利用EKF和GHF算法对SOC进行实时估算,并通过与SOC真实值的对比得到实际估算效果。UDDS工况下SOC估算及分析如图6所示。

图6 SOC估算及分析曲线(UDDS工况)
由图6可以看出,即使在剧烈电流变化的工况下,EKF和GHF算法都能够精确地实时跟踪真实SOC的变化,并且估计GHF算法的估算准确度高于EKF法。两种算法在SOC估算末期出现一定的偏差,这是由于放电末期电池的内阻剧烈变化而导致的。
3.4 算法初值鲁棒性及误差分析
高斯-厄米特滤波算法的另一个优点是对系统的初始值要求不高。在初值和实际值存在偏差的情况下,经过一定时间的迭代修正,能够使得算法输出结果收敛于真实值。因此,该算法对初值具有较好的鲁棒性。为了验证该算法对SOC估算的适用性,分别设置不同的算法初值,并对状态变量SOC的估算结果进行仿真对比。设置GHF算法初值分别为0.5和0.6,并与真实初值SOC=0.7进行对比,结果如图7所示。

图7 鲁棒性对比曲线
从图7可以看出,在初始SOC偏差较大的状态下,经过短短30s的递推更新,SOC都能迅速收敛于真实值。这是由于在对SOC进行迭代估算时,GHF算法对SOC初始值并不敏感,即使SOC的初设定值存在很大的误差,GHF算法在经历一段时间的修正之后也有较好的收敛效果。
为了验证高斯-厄米特算法的收敛性和估算误差,采用初始SOC为0.8的真实值作参考,并设定算法初值为0.7。其主要目的是测试算法的自校准能力。这是因为初始SOC未知,并且很难准确获取。
SOC估算误差曲线如图8所示。
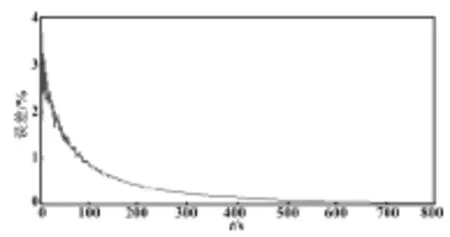
图8 SOC估算误差曲线
从图8可以看出,开始一段时间SOC估算误差较大;随着更多测量值的获取和算法的循环迭代,误差逐渐缩小并趋近于0。整个过程中,最大误差不超过3.7%,具有较高精度。
4 结束语
本文提出了一种基于PNGV模型和高斯-厄米特算法相结合的SOC估算策略,并对方案进行了分析验证。采用PNGV等效电路模型来描述锂离子电池的工作特性,电池的内阻特性和极化特性清晰明确,并可通过HPPC试验识别模型参数。在Matlab/Simulink平台上,对GHF算法的估算效果进行了仿真验证。仿真结果表明:无论是在恒流、周期电流工况下,还是在变电流的工况下,SOC都能实时跟踪真实值的变化;同时,算法对SOC初值具有很好的鲁棒性,且其收敛于真实值的速度较快,在初始SOC为0.8情况下,最大误差不超过3.7%,具有较高的精度。该策略存在的不足是锂离子电池在实际工作过程中还要受到温度、自放电等多种因素的影响,模型参数也随这些因素动态变化。本文中的参数均是在常温下辨识的,下一步可针对温度因素进行完善。
[1] PLETT G L.Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs:Part 1.Background[J].Journal of Power sources,2004,134(2):252-261.
[2] PLETT G L.Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs:Part 2.Modeling and identification[J].Journal of power sources,2004,134(2):
262-276.
[3] PLETT G L.Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs:Part 3.State and parameter estimation[J].Journal of Power Sources,2004,134(2):277-292.
[4] 杨金龙,姬红兵,刘进忙.高斯-厄米特粒子PHD被动测角多目标跟踪算法[J].系统工程与电子技术,2013(3):457-462.
[5] 刘欣,冯新喜,王鹏.自适应高斯-厄米特粒子PHD滤波多目标跟踪算法[J].重庆邮电大学学报(自然科学版),2016(2):280-284.
[6] LI J,JIA B,MAZZOLA M,et al.On-line battery state of charge estimation using Gauss-Hermite quadrature filter[C]//2012 Twenty-Seventh Annual IEEE Applied Power Electronics Conference and Exposition(APEC).IEEE,2012:434-438.
[7] HU X,LI S,PENG H.A comparative study of equivalent circuit models for Li-ion batteries[J].Journal of Power Sources,2012,198:359-367.
[8] The U.S. Department of Energy.PNGV battery test manual[M].3rd.Washington:US Department of Energy,2001.
[9] The U.S.Department of Energy.FreedomCAR battery test manual for power-assist hybrid electric vehicles[N].2003:3-6.
[10]ARASARATNAM I,HAYKIN S,ELLIOTT R J.Discrete-time nonlinear filtering algorithms using Gauss-Hermite quadrature[J].Proceedings of the IEEE,2007,95(5):953-977.
[11]林青,尹建君,张建秋,等.非线性非高斯模型的高斯和滤波算法[J].系统工程与电子技术,2010(12):2493-2499.
[12]JIA B,XIN M,CHENG Y.Sparse Gauss-Hermite quadrature filter with application to spacecraft attitude estimation[J].Journal of Guidance,Control,and Dynamics,2011,34(2):367-379.
[13]JOHNSON V H.Battery performance models in ADVISOR[J].Journal of power sources,2002,110(2):321-329.
ResearchonSOCEstimationBasedonPNGVModelandGauss-HermiteFilter
FAN Xuguo1,ZHOU Jinzhi1,2
(1.School of Information Engineering,Southwest University of Science and Technology,Mianyang 621010,China;2.Sichuan Key Laboratory of Special Environment Robot Technology,Mianyang 621010,China)
In order to solve the problems of low accuracy and poor initial robustness of state of charge(SOC) estimation for lithium-ion battery,a method of estimating the SOC of lithium-ion battery based on partner for a new generation of vehicles(PNGV) equivalent circuit model and Gauss-Hermite filter(GHF) is put forward.Firstly,PNGV model is built to simulate the dynamic and static operating characteristics of the battery,and the state space equations of the equivalent circuit model are listed.Then,the dynamic parameters of the model are recognized by the tests of hybrid pulse power characteristic,and the effectiveness of the model and its parameters are verified by comparing the voltage response under the current excitation.Finally,by combining GHF,the coefficient matrix and recursive process of the algorithm are obtained.On the Matlab/Simulink platform,the estimation effect of the SOC estimation method is simulated,analyzed and validated.The results show that SOC can track the change of real value in real time whatever it is under constant current,periodic constant current and periodic varying current,or the urban dyanometer driving schedule(UDDS) varying current conditions.In addition,the algorithm has good robustness to the initial value,and in the case that the initialSOCis 0.8,the maximum error of SOC estimation is less than 3.7% and has high accuracy,which provides a new idea for the estimation of the lithium-ion battery SOC.
Lithium-ion battery; Battery management system; Equivalent circuit model; Gauss-Hermite filter(GHF); State of charge(SOC); Parameter recognition; Hybrid pulse power characteristic(HPPC)
修改稿收到日期:2017-05-19
特殊环境机器人技术四川省重点试验室基金资助项目(13ZXTK07)、西南科技大学研究生创新基金资助项目(16ycx100)
凡旭国(1991—),男,在读硕士研究生,主要从事电池管理系统、电池状态估算等方向的研究,E-mail:xikexiaofan@163.com;周金治(通信作者),男,硕士,副教授,主要从事电池管理系统、电池组均衡技术等方向的研究,E-mail:zhoujinzhi@swust.edu.cn
TH701;TP301.6
A
10.16086/j.cnki.issn1000-0380.201712006
