差分进化算法综述

2017-12-22丁青锋尹晓宇

智能系统学报 2017年4期

关键词：控制参数差分变异

丁青锋，尹晓宇

(1.华东交通大学电气与自动化工程学院，江西南昌 330013； 2.上海大学特种光纤与光接入重点实验室，上海 200072)

差分进化算法综述

丁青锋1，尹晓宇2

(1.华东交通大学电气与自动化工程学院，江西南昌 330013； 2.上海大学特种光纤与光接入重点实验室，上海 200072)

差分进化算法由于算法结构简单易于执行，并且具有优化效率高、参数设置简单、鲁棒性好等优点，因此差分进化算法吸引了越来越多研究者的关注。本文概述了差分进化算法的基本概念以及存在的问题，综述了差分进化算法的控制参数、差分策略、种群结构以及与其他最优化算法混合等4个方面改进策略并讨论它们各自的优缺点，为差分进化算法下一步的改进提出了参考方向。

差分进化；启发式并行搜索；差分策略；控制参数；种群结构；混合优化；收敛速度；优化效率

随着科技的进步和生产技术的发展，优化问题几乎遍布科学研究及工程实践的各个领域，成为现代科技不可或缺的理论基础和研究方法。而具有启发式和随机特性的进化算法，如遗传算法(genetic algorithm，GA)[1]、进化规划(evolution programming，EP)[2]以及进化策略(evolution strategy，ES)[3]具有算法效率高、易操作以及简单通用等特点，也成为解决现实世界中优化问题的有效工具，取得了一些有效的成果。但随着信息时代的快速发展以及“大数据”的涌现，现在的科学研究以及工程实践中优化问题通常具有规模大、复杂程度高以及包含大量局部最优解等特点，很多优化问题并没有明确的数学解析式，或者其本身就是非确定性多项式难题(non-deterministic polynomial，NP)，现有研究成果及方法远远不能满足。

差分进化算法(differential evolution，DE)作为一种新型、高效的启发式并行搜索技术，通过对现有优化方法进行大胆的扬弃，具有收敛快、控制参数少且设置简单、优化结果稳健等优点[4]，对进化算法的理论和应用研究具有重要的学术意义。但是，标准的DE算法也具有控制参数选择的压力大以及搜索能力与开发能力相矛盾的现象，往往容易造成种群个体早熟收敛、搜索停滞等诸多问题。尤其是对于某些理论计算复杂度较高的工程难题，用标准的DE算法难以有效解决，亟待提出稳健、快速收敛以及精确寻优的改进型DE算法。目前，针对某些特定问题，不少文献提出了很多改进型的DE算法。但是近几年国内很少有文献系统地阐述DE算法优化过程中存在的问题以及研究这些问题所产生的机理，给后续的研究者造成了很大的困扰，同时也使如何选择改进算法变得困难。

1 国内外研究概况

1.1 发展历史

DE算法[5]是由Store和Price于1997年提出的一种基于群体差异的启发式并行搜索方法，提出的初衷是为了求解切比雪夫多项式问题。作为一种基于群体导向的随机搜索技术，DE算法包括初始化、变异、交叉以及选择等操作；与其他优化算法不同在于，DE算法的进化个体扰动是通过多个个体的差分信息来体现的，如图1所示。

图1 二维差分进化算法的进化步骤Fig.1 The evolutional step of 2-D differential evolution

由于DE算法在不同进化阶段个体间的差异性会随之变化，因此不同阶段会出现不同的搜索能力和开发能力：进化初期的个体差异性较大，DE算法将在较大范围内进行搜索最优解，因此这个阶段的搜索能力较强；进化末期种群趋于逐渐收敛的状态，个体间差异性较小，因此这个阶段的开发能力较强。正是这种种群自我调节能力，从而使DE算法具有广泛的适用能力。DE算法作为一种启发式并行搜索方法，因其突出的优化性能受到越来越多研究者的广泛关注。

1.2 研究概况

目前，DE算法已成为进化计算领域的研究热点之一，每年都有大量的研究文献出版。从近几年SCI收录的DE算法论文分布情况可以看出，对差分进化的研究呈逐年上升的趋势，但在数量上还远不及遗传算法及其他优化方法。

DE算法具有非常优秀的寻优能力，大量应用于理论研究与工程实际中，如在信号处理[6]、生物[7]、计算机网络[8]、协同中继[9]、卫星通信[10]、机械设计与机器人[11]、电力电子[12-13]、电力系统[14]、电磁兼容[15]、图像处理[16]、工业控制[17]、天线设计[18]、电子设计[19]等领域都取得了非常显著的效果。DE算法的研究最多的领域为工程、数学、计算机科学和物理，占了研究论文总数的近70%，其他所有学科占了总数的30%左右。可以看出，对DE算法的研究主要集中在工程、数学应用领域。

DE算法性能分析与改进研究，主要针对DE算法两个方面的缺陷进行：1)当种群个体无法继续寻找最优解，停止向全局最优方向进化的现象，即收缩停滞问题；2)种群个体失去多样性，陷入局部最优解的现象，即早熟收敛问题。而国内外学者对其改进策略主要集中在以下4个方面：控制参数设置、进化策略选择、种群结构以及与其他优化算法混合。

目前，DE算法已拓展到多目标优化领域。文献[20]提出基于差分进化算法的多目标优化算法，该算法在变异阶段利用多导向器代替传统的基向量选择解决约束优化问题，另外采用非支配排序法和二级种群求解非支配解；MO-ABC/DE算法[21]则通过结合人工蜂群算法(artificial bee colony，ABC)与DE算法的集体智慧解决非约束多目标优化问题；Coelho等[22]提出一种基于截断伽马概率分布的多目标DE算法用以解决变压器设计问题；Wu等[23]提出MOSADE算法解决混合动力车中部件尺寸与控制策略并行优化问题；Cheng等[24]提出两阶段多目标DE算法解决资源有限项目中的时间-成本权衡问题；为了获得目标表面噪声的非劣最优解，Rakshit等提出3种新的选择策略用以提高多目标DE算法性能；文献[25]提出基于特征提取与集成学习技术的多目标DE算法用于生物实体提取；Caravggi等[26]结合DE算法和SPEA算法用于解决电磁问题。

在国内，孟红云等[27]提出一种基于双群体搜索机制的求解约束多目标优化问题的DE算法；毕晓君等[28]通过云模型对DE算法的参数进行自适应处理，增强算法对解的探索能力；郭俊等[29]利用改进的多目标DE算法解决铝电解多目标优化问题；严细辉等[30]利用模拟退火思想改进多目标DE算法解决以能耗、实际区间运行时间、精确停车及不舒适度为指标建立高速列车运行操纵多目标优化问题。

2 差分进化算法存在的问题

DE算法从生物进化得到启发，利用群体的优势以及并行分布的特点，为解决实际复杂优化问题提供了一种可行途径。但算法中涉及的各种控制参数的设置以及进化策略的选择通常都是依据经验确定的，缺乏理论的分析和指导，因此在进行各种实际复杂问题优化时易陷入局部最优，出现早熟收敛或者搜索停滞等现象[31]。

2.1 差分进化算法的早熟收敛问题

DE算法通常是一种在搜索空间内有效的搜索算法。其中控制参数的设置与进化策略的选择是决定算法性能好坏的关键，一旦选择不当，往往容易造成进化种群过早地失去多样性，使种群个体集中到某一局部最优点，导致种群整体早熟收敛，无法实现向全局最优进化[32]，从图2中可以清楚地看出其全局最优解及局部最优解的分布。一旦进化个体收敛到局部最优解，新生个体很难获得更优解，进而出现早熟收敛的情况。

(a)多峰函数

(b)最优解分布图2 多峰函数的早熟收敛Fig.2 The premature convergence of multi-peaks function

影响DE算法早熟收敛的主要因素可以归纳为以下几点：

1)种群初始化及种群规模。若种群初始化分布在解空间的局部区域，则易造成算法收缩空间受限。如果进化种群过小，容易造成有效等位基因的缺失，从而降低生成具有竞争力的个体可能性进而增加种群早熟收敛的可能性[31]。为了保持足够的种群多样性，避免早熟收敛，种群规模NP应该足够大[33]；但种群规模NP过大则会降低找到正确搜索方向的可能性[31]。

2)控制参数。文献[34]指出，种群个体多样性的丧失是引发种群早熟的直接诱因。为保持种群多样性，控制参数设置是否合适就显得尤为重要。其中收缩因子F需要保持一定的变化范围；交叉因子CR的大小决定种群个体中元素被替代的程度：较小的CR值将造成种群的多样性变化不显著，搜索速度也将变慢；较大的CR值意味着种群多样性更好，但不利于算法的开发能力，因此算法的收敛性能将会受到影响[35]。

3)进化策略：搜索能力与开发能力是差分进化算法性能重要的标准。其中搜索能力推动在更大范围搜索,从而使候选解具有多样性，因此可提高找到全局最优解的可能性，但搜索能力过强则易导致搜索停滞；开发能力推动在局部最优解附近的搜索，因此有利于收敛，但开发能力过强则易导致早熟收敛[36]。进化策略的选择是决定差分进化算法搜索能力与开发能力平衡的关键，不同的进化策略表现出不同的搜索与开发能力的倾向。不同的变异和交叉策略对算法的收敛性能有不同的影响。

针对上述进化种群早熟收敛的问题，很多学者提出了多种改进的方法，通过设置合适参数和选择恰当的进化策略，以希望在算法有效性(候选解的质量)和效率(收敛速度)之间达到平衡，主要手段包括：控制参数调节[37-39]、局部优化[40]和混合其他优化算法[41-42]。其中，局部优化通过在搜索到的最优解附近进行精细搜索，最终实现优化结果精确度的提高。然而，自适应变异策略一方面可以赋予进化算法快速精确地定位局部最优解，另一方面也是易陷入早熟收敛从而导致寻优失败[43]。提高种群的多样性可以增强算法搜索大空间的能力，避免早熟收敛问题的发生；然而，增强种群多元性虽然能搜索到更大的空间，但容易降低种群进化的收敛速度，甚至陷入局部最优从而导致优化失败。

算法整体收敛速度也是DE算法的一个重要指标。虽然已有不少文献提出了许多改进算法，但是针对某些特定问题，其优化结果往往很难令人满意。对于一种优化算法来说，在保证一定收敛速度的同时，避免算法陷入早熟收敛是一个需要平衡的难题。因此，差分进化算法仍需要改进，以适应更多的优化环境。

2.2 差分进化算法的搜索停滞问题

假如进化算法变异、交叉后所产生的进化种群个体比原种群个体的适应度差，则进化个体的更新机制就陷入停顿，即算法的进一步迭代很难产生适应度更好的个体，最终导致搜索停滞现象的发生。如图3所示，若6个候选个体的适应度函数值皆劣于个体A，则个体A将保留到下一代。若个体B、C、D也重复个体A的情况，意味着下一代种群与现有种群相同，即出现搜索停滞的情况。因此虽然种群仍然保持多样性，但无法再进一步收敛。

(a) 现有种群

(b)个体A的候选个体图3 差分进化算法搜索停滞Fig.3 Search stagnation of DE

DE算法出现搜索停滞具有以下两个特征[44]：1)种群个体不收敛；2)个体进化更新机制失效。

当DE算法搜索停滞发生时，停滞特征1)可以用第G代的目标个体与其重心之间的平均距离来描述：

DE算法发生搜索停滞时的特征2)可以用第G代目标个体最近连续未更新次数来描述：

式中：nui,G为第G代目标个体i未最近连续更新次数，初值为0，i=1,2,…,NP。若nui,G持续增加，则说明DE算法无法为目标个体i产生极值解。

克服进化算法搜索停滞的一般方法是在算法中引入能够在整个解空间中进行广泛搜索的策略，另外通过jitter/dither扰动技术，也可以降低搜索停滞出现的概率[45]。在不改变种群规模的情况下，文献[46]指出，通过收缩因子F和增大交叉因子CR可以增加种群个体的多样性；文献[33]指出，通过设置收缩因子F在进化过程中为随机数，可以有效增加候选个体的数量，实现算法稳定性的提高。

也有学者[47]为平衡算法集中搜索与多样化搜索策略之间的矛盾，提出外在的种群多样化测度方法，根据群体多样化测度值在算法的不同搜索阶段使用不同搜索策略，从而克服搜索停滞的缺陷。但群体多样化测度方法通常是针对某一算法构造的，缺乏对搜索停滞的起因、表现特征深入系统的研究，因此具有较大的局限性。

在研究DE算法大量文献中，很少提及搜索停滞问题产生机理。文献[48]进一步对群体优化算法的搜索机理进行探讨，针对集中化搜索与多样化搜索对进化停滞的影响进行了研究，从而证明了集中化搜索策略具有将候选解趋于单一化的特点，是导致算法搜索停滞的主要原因；而多样化搜索策略则具有将候选解泛化的特点，即从任何一个候选解可以搜索到整个解空间的任意一点，但其缺点是使算法不收敛。文献[44]指出，无法确切地发现搜素停滞的原理，但是通过增加种群个体的多样性及规模可以在一定程度上降低该问题出现的概率。

3 差分进化算法的改进策略

针对DE算法的理论研究主要集中在如何提高算法的寻优能力、收敛速度以及克服启发式算法常见的早熟收敛以及搜索停滞等缺陷方面。近年来，研究人员从多个角度不断改进算法以适应更为复杂的优化问题和满足更高的求解质量，改进算法大致分为控制参数设置、差分策略选择、种群结构以及与其他最优化算法混合等四大类。

1)控制参数

DE算法的控制参数主要有种群规模NP、缩放因子F以及交叉概率CR。如果参数选择不恰当，可能会由于过度强调搜索能力导致算法搜索停滞或者过度强调开发能力导致算法早熟收敛。其中种群规模主要影响种群的多样性以及收敛速度：增大NP可以提高种群的多样性，但同时降低种群的收敛速度；减小NP可以提高收敛速度，但易导致早熟收敛。缩放因子F主要影响搜索步长：增大F可以增加算法的搜索范围，提高种群多样性但同时消弱算法的开发能力；减小F可以增加算法的开发能力，提高算法的收敛速度，但同时陷入早熟收敛的风险。交叉概率CR影响进化信息的调整权重：增大CR可以提高种群多样性；减小CR有利于分析个体各维可分离问题[33]。图4展示了hybrid_func2函数在不同CR情况下的候选个体分布情况，可以看出随着CR的增加种群的多样性得到提高。

(a)CR=0.0

(b)CR=0.5

(c)CR=1.0 图4 不同交叉因子的候选个体分布Fig.4 Distribution of the candiate individuals with differental CR

关于控制参数设置的研究主要集中在以下3种方式：固定、随机以及自适应。在经典DE算法中采用的是参数固定设置的方式，即参数在搜索之前预先设置好并且在整个迭代过程中保持不变，Storn和Price在文献[5]中参数的设置如下：种群个数NP为5D到10D(D为个体的维度)；缩放因子F为0.5；交叉概率CR初值一般情况下设置为0.1，快速收敛需求时设为0.9。然而，Gämperle等在文献[49]中总结测试结果时得出DE算法的表现严重依赖于控制参数的设置，控制参数设置为：种群个数NP理想区间为3D～8D；缩放因子F有效初值为0.6；交叉概率CR初值理想区间为0.3～0.9。Rönkkönen等[50]认为：种群个数NP理想区间为2D～40D；缩放因子F应在0.4～0.95(其中F为0.9时可实现搜索与开发能力的妥协)；对于可分离问题，交叉概率CR理想区间为0.0～0.2，对于不可分离问题或者多峰问题，则设置为0.9～1。CoDE[51]则采用每个实验向量从3个预先设置的参数池中随机选取的方式。ODE[52]采用正交交叉算子提高算法的搜索能力，其参数设置为F=0.9，CR=0.9，NP=D；DE-APC[53]采取自动参数配置的方法，即每个个体的进化控制参数F和CR分别从两个预先设置好的参数集合中随机选取。因此从上述结论表明，固定参数设置不可能适合所有问题，参数应基于待优化问题而设。

为了避免人工调节控制参数，其中一种方法就是随机设置，线性变化、概率分布以及特定启发式规则是3种常见的随机参数设置方法。Das等[45]提出参数F两种设置的方法：随机设置和时变设置，其中随机方式中参数F被设置为0.5～1的随机数，而时变方式中参数F在给定的时间间隔呈线性降低；SaDE[37]算法中参数F选取满足正态分布N(0.5, 0.3)。控制参数的随机设置通过增加搜索的多样性提高算法的搜索能力。

另一种参数设置的方法为自适应调节方式，即依据搜索过程的反馈[38,54]或者经过进化操作[55-56]实现控制参数调节。结合历代个体和相对目标函数值作为输入，Liu等[54]提出利用模糊逻辑控制器自适应调节算法控制参数的FADE算法；Brest等[38]提出jDE算法，其控制参数F和CR分别以概率为τ1和τ2自适应在[0.1,1.0]和[0.0,1.0]范围中指定；在JADE算法[39]中，依据历史成功参数信息，参数F产生满足柯西分布而参数CR满足正态分布；文献[57]提出的SHADE算法是基于不同成功历史机制更新参数F和CR的改进型JADE；SaDE[37]中参数CR设置满足基于以前成功CR值为均值的正态分布；文献[58]依据相关成功率以一定概率从一个参数集合中自适应选择；PVADE算法[59]提出通过各维差分度量计算缩放因子向量代替单个缩放因子。

2)差分策略

DE算法主要特性就是差分策略，可以描述为DE/x/y/z，其中参数x表示参与变异的向量，可以是随机向量(rand)、当前种群的最优向量(best)或者是当前向量本身(current)；参数y表示参与变异的差分向量数目；参数z表示交叉的模式，如二项式交叉、指数交叉以及正交交叉。其中DE/rand/1/bin和DE/best/2/bin是目前应用最为广泛的差分策略，其中第1种策略有利于保持种群多样性，第2种策略有利于提高算法的收敛速度。此外Fan等还提出一种三角形差分策略。

近几年来，研究者发展了大量不同的变异策略[35,60]。其中一部分具有良好的搜索能力的策略，适合于全局搜索；另一部分具有良好的开发能力的策略适合于局部搜索[5]。例如，相对于单个差分向量的策略(如，DE/rand/1)，具有两个差分向量(如，DE/rand/2)的变异策略可以提高种群的多样性；如采用最佳向量作为当前基向量的变异策略(如，DE/best/1 and DE/current-to-best/1)则可以增强算法的开发能力从而加快收敛的速度。

然而，为了提高算法的稳健性、搜索能力和开发能力必须同时考虑进化策略。因此，一类采用单一操作变异策略结合搜索特性的改进DE算法被提出，Epitropakis等[61]提出将搜索与开发变异操作算子线性混合的方法平衡两者冲突的BDE算法，Das等[62]提出将全局与局部变异个体结合组成进化代数相关比重变异个体的DEGL，由Zhang等[39]提出利用一个外部的备份结合利用历史信息的DE/current-to-pbest/1差分策略指导个体搜索JADE，Tang等[63]结合3个不同的差分向量和DE/current-to-pbest/1差分策略以提高种群的多样性而提出PIDE，Epitropakis等[64]提出选择试验个体的邻居参与变异操作的ProDE，最佳随机变异策略的BoRDE[65]，三角变异策略的TDE[66]。另一类采用多变异算子集合不同搜索特性的改进DE算法，如：差分策略自适应的SaDE[67]，教-学自适应的TLBSaDE[68]，结合试验向量代数策略和控制参数的CoDE[69]，采用一组候选变异策略和控制参数的EPSDE[70]、超适合多标准自适应的SMADE[71]、jDEsoo[72]、小种群多变异策略的SPSRDEMMS[73]、基于等级变异策略的Rank-DE[74]。

DE算法的操作除了上述变异和交叉两种操作算子之外还包括初始化以及选择操作。其中初始化方式有随机初始化以及反学习初始化[75]；选择操作是依据评价标准解决个体丢弃，从而维持种群多样性信息的问题。文献[46]为了平衡搜索能力与开发能力，提出以进化代数为函数的选择策略，但该选择策略易收到最大进化代数以及待优化问题的复杂性影响；文献[76]提出与当前个体进化时间以及其更新次数相关的选择策略，保证在进化初期适应度较差的个体也有一定的生存概率，从而有利于保持种群的多样性，而在进化后期个体的生存则依赖于其自身的适应度，从而加速种群的收敛。

3)种群结构

具有启发式和随机特性的进化算法已被证明是解决实际应用中复杂优化问题的有效工具。但是随着问题规模以及复杂性的日益增大，搜索的空间、数量庞大的局部最优以及适应性评估计算的成本将变得非常高，因此传统的进化算法无法在合理的时间里得出满意的结果。分布式进化算法(dEA)通过将机制种群分配到分布式结构中，利用分而治之机制的分布式协同进化解决高维问题。此外，其分布式结构非常有利于保持种群多样性，从而有效避免陷入局部最优，同时有利于实现多目标搜索。当分布式种群结构中多个种群独立进行进化搜索时，即使单个种群出现多样性丧失，由于种群间存在的差异性，通过种群间的信息交换与共享，依然可以保证整个算法的进化。分布式种群结构分为主从模型[77]、岛屿模型(又称粗颗粒模型)[78]、元胞模型(又称细颗粒模型)[79]、等级模型[80]以及水池模型[81]等，如图5所示，进化任务可在种群级、个体级甚至操作级并行执行。

(a)主从模型

(b)岛屿模型

(c)元胞模型

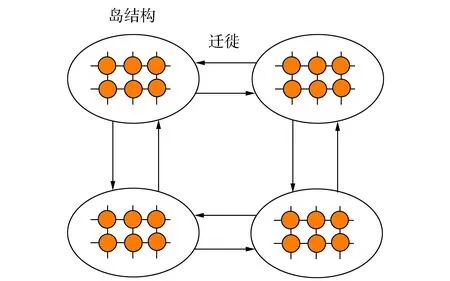
(d)等级模型(岛屿-元胞)

(e)水池模型图5 典型分布式种群结构Fig.5 Typical structure of distributed population

文献[82]提出基于异步主从模型的多目标优化算法AMS-DEMO，用以解决同质/异质并行计算机体系结构的时间密度问题；为了解决生物信息学中超复杂度的蛋白质结构预测问题(protein structure prediction，PSP)，Kalegari等[83]提出基于集群信息传输接口的并行主从结构差分进化算法，利用Toy模型重新表述二维/三维的蛋白质结构。Kushida等[84]通过将进化算法种群分割成大小不等的子种群(岛屿)且分配不同的控制参数，从而实现子种群的并行进化，同时通过岛屿间的个体迁徙保持种群的多样性；文献[85]提出基于“随机交配迁徙”交换岛屿间信息和“往返行程”更新相应岛屿两种技术的IbDE算法。Alba等[86]为了平衡算法搜索能力与开发能力之间的冲突，以种群邻居比例作为参数建立一种自适应动态元胞模型，同时为不同的优化问题设计相应的元胞网络；Dorronsoro等[87]提出基于元胞个体质量自我管理的邻居结构以及按照收敛速度设置最佳的种群结构；文献[88]利用元胞进化特性与蚁群优化解决几何约束优化问题；Lu等[89]提出基于元胞进化规则的元胞遗传算法，并且给出了元胞进化规则选择标准从而保持种群的多样性；Noman[90]和Dorronsoro[91]提出线型和紧密型元胞邻居结构的差分进化算法；Noroozi等[92]提出CellularDE算法解决动态优化问题，该算法将搜索空间分布到元胞网格中但是没有考虑元胞自身的进化。文献[93]中，等级模型算法中的种群被分成若干个子种群，它们由各自进化并在特定时刻进行相互通信，所提出的岛屿-主从式等级算法的速度是线性的；Folino等[94]提出一种分布遗传规划算法，其种群由多个独立岛屿组成，每个岛屿种群采用独立的元胞遗传规划算法；Herrera等[95]指出等级模型的关键问题是发展了全局和局部两种种群迁徙方式，这是基本分布式进化算法与等级分布进化算法的区别；另外，这种等级模型的优点还包括提高每个节点的效率、更多样化合作以及同质/异质的良好结合等。文献[96]提出一种分布式存储池结构进化算法，处理器将个体从存储池中提取执行进化操作后再放回到池中，从而克服传统分布进化算法松散耦合、不可靠的缺陷。

4)与其他最优化算法混合

与其他最优化算法混合主要有以下3种方式：将其他最优化算法的优化算子嵌入DE算法的差分策略以改进DE算法；将DE算法的差分策略嵌入其他最优化算法的优化算子以改进其他最优化算法；迭代过程分别由差分进化算法与其他最优化算法完成，所获得种群多样性的优化算法。

其中，文献[41-42]分别提出利用粒子群算子与人工蚁群算子改进DE算法；邓泽喜等[97]提出一种基于小生境的混沌变异DE算法,以提高算法在搜索初始阶段的种群多样性。詹腾等[98]针对在多目标优化算法存在收敛性不佳以及解分布性差的问题，通过多策略差分协同进化选择算子，提出基于多策略差分进化的多目标遗传算法。为解决多目标柔性车间工作调度问题，Zhang等[99]提出免疫克隆DE算法，利用DE算法和免疫克隆算法分别进行种群进化，通过两种群之间的个体迁徙平衡算法搜索能力和收敛速度。

4 总结与展望

目前，DE算法已经广泛应用在求解各类静态优化问题上。然而，DE算法也存在早熟收敛和搜索停滞等缺陷，限制了其优化能力和应用范围，特别是应用于求解动态优化问题，迫切需要加以研究和改进。有研究者利用混沌理论、协同量子等改善DE算法的性能。DE算法从最初的静态单目标优化发展到现在的动态多目标优化，已经有了长足的进步，但面对不断涌现的新的优化问题，仍然需要不断地进行方法、策略等创新。下面列出几个具体待研究的问题以供参考：

1)从理论上，DE算法的性能主要是由其控制参数、种群进化策略等因素决定的，如何保证其一定代数收敛程度一直是进化算法非常重要的研究问题。考虑如何将现有凸优化方法与进化算法结合，提出针对性的分阶段优化策略。

2)现阶段对进化算法的研究主要针对其控制参数的调制以及交叉、变异策略的设计等，忽视了快速变化环境下优化结果实时性的问题。现有算法主要考虑的是对种群规模、进化个体淘汰机制以及邻居选择等方面的控制。在以后的研究中还可以考虑针对动态多目标优化问题，如何适应快速变化环境以及种群优化方向的快速预测等。

[1]HOLLAND J H. Adaptation in natural and artificial systems[M]. MA: MIT press, 1975.

[2]FOGEL L J. Artificial intelligence through simulated evolution[M]. New York: John Wiley, 1966.

[3]RECHENBERG I. Evolutions strategie: optimierung texhnischer systeme nach prinzipien der biologischen evolution[M]. Stuttgart, Gemany: Frogmann Holzboog, 1973.

[4]FERRANTE N, VILLE T. Recent advances in differential evolution: a survey and experimental analysis[J]. Artificial intelligence, 2010, 33(1/2): 61-106.

[5]STORN R, PRICE K. Differential evolution: a simple and efficient heuristic for global optimization over continuous spaces[J]. Journal global optimization, 1997, 11(4): 341-359.

[6]GAO Z Q, PAN Z B, GAO J H. A new highly efficient differential evolution scheme and its application to waveform inversion[J]. IEEE geoscience and remote sensing letters, 2014, 11(10): 1702-1706.

[7]ZHAN C J, SITU W C, YEUNG L F, et al. A parameter estimation method for biological systems modelled by ode/dde models using spline approximation and differential evolution algorithm[J]. IEEE/ACM transactions on computational biology and bioinformatics, 2014, 11(6): 1066-1076.

[8]LEI H, LI L, WU C H. Evolutionary model selection and parameter estimation for protein-protein interaction network based on differential evolution algorithm[J]. IEEE/ACM transactions on computational biology and bioinformatics, 2015, 12(3): 622-631.

[9]SHARMA N, ANPALAGAN A. Composite differential evolution aided channel allocation in OFDMA systems with proportional rate constraints[J]. Journal of communications and networks, 2014, 16(5): 523-533.

[10]DING Y, JIAO Y C, ZHANG L, et al. Solving port selection problem in multiple beam antenna satellite communication system by using differential evolution algorithm[J]. IEEE transactions on antennas and propagation, 2014, 62(10): 5357-5361.

[11]KRANJCIC D, STUMBERGER G. Differential evolution-based identification of the nonlinear Kaplan turbine model[J]. IEEE Transactions on energy conversion, 2014, 29(1): 178-187.

[12]YAHIA H, LIOUANE N, DHIFAOUI R. Differential evolution method-based output power optimization of switched reluctance generator for wind turbine applications[J]. IET renewable power generation, 2014, 8(7): 795-806.

[13]MARCIC T, STUMBERGER B, STUMBERGER G. Differential-evolution-based parameter identification of a line-start IPM synchronous motor[J]. IEEE transactions on industrial electronics, 2014, 61(11): 5921-5929.

[14]BASETTI V, CHANDEL A K. Hybrid power system state estimation using Taguchi differential evolution algorithm[J]. IET science, measurement and technology, 2015, 9(4): 449-466.

[15]XUE Y, ZHUANG Y, NI T Q, et al. Self-adaptive learning based discrete differential evolution algorithm for solving CJWTA problem[J]. Journal of systems engineering and electronics, 2014, 25(1): 59-68.

[16]ZHONG Y F, ZHAO L, ZHANG L P. An adaptive differential evolution endmember extraction algorithm for hyperspectral remote sensing imagery[J]. IEEE geoscience and remote sensing letters, 2014, 11(6): 1061-1065.

[17]TANG L X, ZHAO Y, LIU J Y. An improved differential evolution algorithm for practical dynamic scheduling in steelmaking-continuous casting production[J]. IEEE transactions on evolutionary computation, 2014, 18(2): 209-225.

[18]MANGOUD M A, ELRAGAL H M, ALASHARA M T. Design of time modulated concentric circular and concentric hexagonal antenna array using hybrid enhanced particle swarm optimisation and differential evolution algorithm[J]. IET microwaves, antennas and propagation, 2014, 8(9): 657-665.

[19]CUKOVIC J P, KLOPCIC B, PETRUN M, et al. Optimization of resistance spot welding transformer windings using analytical successive approximation and differential evolution[J]. IEEE transactions on magnetics, 2014, 50(4): 1-4.

[20]BAATAR N, PHAM M T, KOH C S. Multiguiders and non-dominate ranking differential evolution algorithm for multiobjective global optimization of electromagnetic problems[J]. IEEE transactions on magnetics, 2013, 49(5): 2105-2108.

[21]RUBIO L A, GONZALEZ-ALVAREZ D L, VEGA-RODRIGUEZM A, et al. MO-ABC/DE-multiobjective artificial bee colony with differential evolution for unconstrained multiobjective optimization[C]//Proceedings of the IEEE 13th International Symposium on Computational Intelligence and Informatics. Budapest, Hungary, 2012: 157-162.

[22]COELHO L D S, MARIANI V C, FERREIRA D L, et al. Novel gamma differential evolution approach for multiobjective transformer design optimization[J]. IEEE transactions on magnetics, 2013, 49(5): 2121-2124.

[23]WU L H, WANG Y N, YUAN X F, et al. Multiobjective optimization of HEV fuel economy and emissions using the self-adaptive differential evolution algorithm[J]. IEEE transactions on vehicular technology, 2011, 60(6): 2458-2470.

[24]CHENG M Y, TRAN D H. Two-phase differential evolution for the multiobjective optimization of time-cost tradeoffs in resource-constrained construction projects[J]. IEEE transactions on engineering management, 2014, 61(3): 450-461.

[25]SIKDAR U K, EKBAL A, SAHA S. Differential evolution based multiobjective optimization for biomedical entity extraction[C]//Proceeding of the International Conference on Advances in Computing, Communications and Informatics. New Delhi, India, 2014:1039-1044.

[26]CARAVGGI T G, LEBENSZTAJN L. A multiobjective approach of differential evolution optimization applied to electromagnetic problems[J]. IEEE transactions on magnetics, 2014, 50(2): 625-628.

[27]孟红云,张小华,刘三阳. 用于约束多目标优化问题的双群体差分进化算法[J].计算机学报, 2008, 31(2): 228-235.

MENG Hongyun, ZHANG Xiaohua, LIU Sanyang. A differential evolution based on double populations for constrained multi-objective optimization problem[J]. Chinese journal of computer, 2008, 31(2): 228-235.

[28]毕晓君,刘国安. 基于云差分进化算法的约束多目标优化实现[J]. 哈尔滨工程大学学报, 2012, 33(8): 1022-1031.

BI Xiaojun, LIU Guoan. A cloud differential evolutionary algorithm for constrained multi-objective optimization[J]. Journal of Harbin engineering university, 2012, 33(8): 1022-1031.

[29]郭俊,桂卫华,阳春华. 改进差分进化算法在铝电解多目标优化中的应用[J].中南大学学报:自然科学版, 2012, 43(1): 184-188.

GUO Jun, GUI Weihua, YANG Chunhua. An improved hybrid differential evolution algorithm used for multi-objective optimization of aluminum electrolysis[J]. Journal of central south university, 2012, 43(1): 184-188.

[30]严细辉,蔡伯根,宁滨,等. 基于差分进化的高速列车运行操纵的多目标优化研究[J]. 铁道学报, 2013, 35(9): 65-71.

YAN Xihui, CAI Bogen, NING Bin, et al. Research on multi-objective high-speed train operation optimization based on differential evolution[J]. Journal of the China railway society, 2013, 35(9): 65-71.

[31]YANG M, LI C H, CAI Z H, et al. Differential evolution with auto-enhanced population diversity[J]. IEEE transactions on cybernetics, 2015, 45(2): 302-315.

[32]MUSRRAT A, MILLIE P, SINGH V P. An improved differential evolution algorithm for real parameter optimization problems[J]. International journal of recent trends in engineering, 2009, 1(5): 63-65.

[33]PRICE K, STORE R, LAMPINCN J. Differential evolution-a practical approach to global optimization[M]. New York: Springer, 2005.

[34]ZAHARIE D. Critical values for the control parameters of differential evolution algorithm[C]//Proceedings of 8th International Mendel Conference on Soft Computing. Brno, Czech Republic, 2002: 62-67.

[35]DAS S, SUGANTHAN P N. Differential evolution: a survey of the state-of-the-art[J]. IEEE transactions on evolutionary computation, 2011, 15(1): 4-31.

[36]TANG L, DONG Y, LIU J. Differential evolution with an individual-dependent mechanism[J]. IEEE transactions on evolutionary computation, 2015, 19(4): 560-574.

[37]QIN A K, HUANG V L, SUGANTHAN P N. Differential evolution algorithm with strategy adaptation for global numerical optimization[J]. IEEE transactions on evolutionary computation, 2009, 13(2): 398-417.

[38]BREST J, GREINER S, BOSKOVIC B, et al. Self-adapting control parameters in differential evolution: a comparative study on numerical benchmark problems[J]. IEEE transactions on evolutionary computation, 2006, 10(6): 646-657.

[39]ZHANG J, SANDERSON A C. JADE: adaptive differential evolution with optional external archive[J]. IEEE transactions on evolutionary computation, 2009, 13(5): 945-958.

[40]AHADZADEH B, MENHAJ M B. A modified differential evolution algorithm based on a new mutation strategy and chaos local search for optimization problems[C]//Proceedings of the 4th International Conference on Computer and Knowledge Engineering. Mashhad, Iran, 2014: 468-473.

[41]SAHU B K, PATI S, PANDA S. Hybrid differential evolution particle swarm optimisation optimised fuzzy proportional-integral derivative controller for automatic generation control of interconnected power system[J]. IET generation, transmission and distribution, 2014, 8(11): 1789-1800.

[42]CHIOU J P, CHANG C F, SU CT. Ant direction hybrid differential evolution for solving large capacitor placement problems[J]. IEEE transactions on power systems, 2004, 19(4): 1794-1800.

[43]RUDOLPH G. Self-adaptive mutations may lead to premature convergence[J]. IEEE transactions on evolutionary computation, 2001, 5(4): 410-414.

[44]LAMPINEN J, ZELINKA I. On stagnation of the differential evolution algorithm[C]//Proceedings of the 6th International Mendel Conference on Soft Computing. Brno, Czech Republic, 2000: 76-83.

[45]DAS S, KONAR A, CHAKRABORTY U K. Two improved differential evolution schemes for faster global search[C]//Proceedings of the Genetic Evolutionary Computation. Washington DC, USA, 2005: 991-998.

[46]STORN R. Differential evolution research-trends and open questions[J]. Study in computational intelligence, 2008, 143: 1-31.

[47]邓可,林杰,张鹏. 基于信息熵的异类多种群蚁群算法[J].计算机工程与应用, 2008, 44(36): 16-19.

DENG Ke, LIN Jie, ZHANG Peng. Multiple heterogeneous ant colonies algorithm based on information entropy[J]. Computer engineering and applications, 2008, 44(36): 16-19.

[48]陈俊风,吴铁军.群体智能算法搜索策略的性质及对停滞现象的影响[J].系统工程理论与实践, 2013, 06: 1587-1595.

CHEN Junfeng, WU Tiejun. The property of search strategies of swarm intelligent algorithms and their influences on stagnation[J]. Systems engineering-theory and practice, 2013, 06: 1587-1595.

[50]RÖNKKÖNEN J, KUKKONEN S, PRICE K V. Real-parameter optimization with differential evolution[C]//Proceedings of the IEEE Congress Evolutionary Computation. Edinburgh, UK, 2005, 1: 506-513.

[51]WANG Y, CAI Z, ZHANG Q. Differential evolution with composite trial vector generation strategies and control parameters[J]. IEEE transactions evolutionary computation, 2011, 15(1): 55-66.

[52]WANG Y, CAI Z, ZHANG Q. Enhancing the search ability of differential evolution through orthogonal crossover[J]. Information science, 2012, 185(1): 153-177.

[53]ELSAYED S M, SARKER R A, RAR T. Differential evolution with automatic parameter configuration for solving the CEC2013 competition on real-parameter optimization[C]//Proceedings of the IEEE Congress Evolution Computation. Cancun, Mexico, 2013: 1932-1937.

[54]LIU J, LAMPINEN J. A fuzzy adaptive differential evolution algorithm[C]//Proceedings of the IEEE Region 10 Conference on Computers, Communications, Control and Power Engineering. Beijing, China, 2002, 9(6): 606-611.

[55]BBASS H A. The self-adaptive Pareto differential evolution algorithm[C]//Proceedings of the IEEE Congress on Evolutionary Computation. Honolulu, HI, USA, 2002: 831-836.

[56]TEO J. Exploring dynamic self-adaptive populations in differential evolution[J]. Soft computation, 2006, 10(8): 673-686.

[57]TANABE R, FUKUNAGA A. Success-history based parameter adaptation for differential evolution[C]//Proceedings of the IEEE Congress on Evolutionary Computation. Cancun, Mexico, 2013: 71-78.

[59]COELHO L S, AYALA H V H, FREIRE R Z. Population’s variance based adaptive differential evolution for real parameter optimization[C]//Proceedings of the IEEE Congress on Evolutionary Computation. Cancun, Mexico, 2013: 1672-1677.

[60]NERI F, TIRRONEN V. Recent advances in differential evolution: a survey and experimental analysis[J]. Artificial intelligence review, 2010, 33(1): 61-106.

[61]EPITROPAKIS M G, PLAGIANAKOS VP, VRAHATIS M N. Balancing the exploration and exploitation capabilities of the differential evolution algorithm[C]//Proceedings of the IEEE Congress on Evolutionary Computation. Hong Kong, 2008: 2686-2693.

[62]DAS S, ABRAHAM A, CHAKRABORTY U K, et al. Differential evolution using a neighborhood based mutation operator[J]. IEEE transactions on evolutionary computation, 2009, 13(3): 526-553.

[63]TANG L, ZHAO Y, LIU J. An improved differential evolution algorithm for practical dynamic scheduling in steelmaking-continuous casting production[J]. IEEE transactions on evolutionary computation, 2014, 18(2): 209-225.

[64]EPITROPAKIS M G, TASOULIS D K, PAVLIDIS N G, et al. Enhancing differential evolution utilizing proximity based mutation operators[J]. IEEE transactions on evolutionary computation, 2011, 15(1): 99-119.

[65]LIN C, QING A, FENG Q. A new differential mutation base generator for differential evolution[J]. Journal of global optimization, 2011, 49(1): 69-90.

[66]FAN H Y, LAMPINEN J. A trigonometric mutation operation to differential evolution[J]. Journal of global optimization, 2003, 27(1): 105-129.

[67]QIN A K, SUGANTHAN P N. Self-adaptive differential evolution algorithm for numerical optimization[C]//Proceedings of the IEEE Congress on Evolutionary Computation. Edinburgh, Scotland, UK, 2005: 1785-1791.

[68]BISWAS S, KUNDU S, DAS S, et al. Teaching and learning best differential evolution with self adaptation for real parameter optimization[C]//Proceedings of the IEEE Congress on Evolutionary Computation. Cancun, Mexico, 2013: 1115-1122.

[69]WANG Y, CAI Z, ZHANG Q. Differential evolution with composite trial vector generation strategies and control parameters[J]. IEEE transactions on evolutionary computation, 2011, 15(1): 55-66.

[70]MALLIPEDDI R, SUGANTHAN P N, PAN Q K, et al. Differential evolution algorithm with ensemble of parameters and mutation strategies[J]. Applied soft computing, 2011, 11(2): 1679-1696.

[71]CARAFFINI F. Super-fit multicriteria adaptive differential evolution[C]//Proceedings of the IEEE Congress on Evolutionary Computation. Cancun, Mexico, 2013: 1678-1685.

[72]BREST J, BOKOVI☞ B, ZAMUDA A, et al. Mezura-Montes, real parameter single objective optimization using self-adaptive differential evolution algorithm with more strategies[C]//Proceedings of the IEEE Congress on Evolutionary Computation. Cancun, Mexico, 2013: 337-383.

[73]ZAMUDA A, BREST J, MEZURA-MONTES E. Structured population size reduction differential evolution with multiple mutation strategies on CEC 2013 real parameter optimization[C]//Proceedings of the IEEE Congress on Evolutionary Computation. Cancun, Mexico, 2013: 1925-1931.

[74]GONG W, CAI Z. Differential evolution with ranking-based mutation operators[J]. IEEE transactions on cybernetics, 2013, 43(6): 2066-2081.

[75]LI H, ZHANG L, JIAO Y C. Solution for integer linear bilevel programming problems using orthogonal genetic algorithm[J]. Journal of systems engineering and electronics, 2014, 25(3): 443-451.

[76]SCHMIDT H, THIERAUF G. A Combined heuristic optimization technique[J]. Advances in engineering software, 2005, 36(1): 11-19.

[77]DUBREUIL M, GAGNÉC, PARIZEAU M. Analysis of a master-slave architecturefor distributed evolutionary computations[J]. IEEE transactions on systems, man and cybernetics, part B (cybernetics), 2006, 36(1): 229-235.

[78]HERRERA F, LOZANO M. Gradual distributed real-coded genetic algorithms[J]. IEEE transactions on evolutionary computation, 2000, 4(1): 43-63.

[79]ALBA E, DORRONSORO B. The exploration/ exploitation tradeoff in dynamic cellular genetic algorithms[J]. IEEE transactions on evolutionary computation, 2005, 9(2): 126-142.

[80]FOLINO G, PIZZUTI C, SPEZZANO G. Training distributed GP ensemble with aselective algorithm based on clustering and pruning for pattern classification[J]. IEEE transactions on evolutionary computation, 2008, 12(4): 458-468.

[81]ROY G, LEE H, WELCH J L, et al. A distributed poolarchitecture for genetic algorithms[C]//Proceedings of the IEEE Congress on Evolutionary Computation, 2009: 1177-1184.

[82]DEPOLLI M, TROBEC R, FILIPIC B. Asynchronous master-slave parallelization of differential evolution for multi-objective optimization[J]. Evolutionary computation, 2013, 21(2): 261-291.

[83]KALEGARI D H, LOPES H S. An improved parallel differential evolution approach for protein structure prediction using both 2D and 3D off-lattice models[C]//Proceedings of the IEEE Symposium on Differential Evolution. Singapore, 2013: 143-150.

[84]KUSHIDA J I, HARA A, TAKAHAMA T, et al. Island-based differential evolution with varying subpopulation size[C]//Proceedings of the IEEE 6th International Workshop on Computational Intelligence and Applications.Hiroshima, Japan, 2013: 119-124.

[85]TAGAWA K, NAKAJIAMA K. Island-based differential evolution with panmictic migration for multi-core CPUs[C]//Proceedings of the IEEE Congress on Evolutionary Computation. Cancun, Mexico, 2013: 852-859.

[86]ALBA E, DORRONSORO B. The exploration/ exploitation tradeoff in dynamic cellular genetic algorithms[J]. IEEE transactions on evolutionary computation, 2005, 9(2): 126-142.

[87]DORRONSORO B, BOUVRY P L. Cellular genetic algorithms without additional parametres[J]. Journal of supercomputing, 2012, 63(3): 816-835.

[88]CAO C, WANG L, ZHAO D. The research based on the discrete cellular ant algorithm in the geometric constraint solving[J]. Acta electronica sinica, 2011, 39(5): 1127-1130.

[89]LU Y, LI M, LI L. The cellular genetic algorithm with evolutionary rule[J]. Acta electronica sinica, 2010, 38(7): 1603-1607.

[90]NOMAN N, IBA H. Cellular differential evolution algorithm[C]//Proceedings of the Advances in Artificial Intelligence. Berlin Heidelberg: Springer, 2011: 293-302.

[91]DORRONSORO B, BOUVRY P. Differential evolution algorithms with cellular populations[C]//Proceedings of the PPSN XI, Part II, LNCS 6239. Berlin Heidelberg: Springer, 2010: 320-330.

[92]NOROOZI V, HASHEMI A, MEYBODI M. CellularDE: a cellular based differential evolution for dynamic optimization problems[C]//Proceedings of the adaptive and natural computing algorithms. Berlin Heidelberg: Springer, 2011: 340-349.

[93]BURCZYNSKI T, KUS W, DUGOSZ A, et al. Optimization and defect identification using distributed evolutionary algorithms[J]. Engineering applications artificial intelligence, 2004, 17(4): 337-344.

[94]FOLINO G, SPEZZANO G. P-cage: an environment for evolutionary computation in peer-to-peer systems[J]. Genetic programming, 2006， 12(12): 341-350.

[95]HERRERA F, LOZANO M, MORAGA C. Hierarchical distributed genetic algorithms[J]. International journal of intelligence systems. 1999, 14(11): 1099-1121.

[96]ROY G, LEE H, WELCH J L, et al. A distributed pool architecture for genetic algorithms[C]//Proceedings of the IEEE Congress on Evolutionary Computation. Trondheim, Norway, 2009: 1177-1184.

[97]邓泽喜,刘晓冀. 基于小生境的混沌变异差分进化算法[J].计算机工程与应用, 2010, 25: 31-33.

DENG Zexi, LIU Xiaoji. Chaotic mutation differential evolution algorithm combined with niche[J]. Computer engineering and applications, 2010, 25: 31-33.

[98]詹腾,张屹,朱大林,等.基于多策略差分进化的元胞多目标遗传算法[J]. 计算机集成制造系统, 2014, 06: 1342-1351.

ZHAN Teng, ZHANG Yi, ZHU Dalin, et al. Cellular multi-objective genetic algorithm based on multi-strategy differential evolution[J]. Computer integrated manufacturing systems, 2014,06: 1342-1351.

[99]ZHANG J, ZHANG Y H, QIN P. Immune clonal differential evolution algorithm for multi-objective flexible job-shop scheduling problem[C]//Proceedings of the International Conference on Artificial Intelligence and Education (ICAIE). Hangzhou, China, 2010: 73-76.

Researchsurveyofdifferentialevolutionalgorithms

DING Qingfeng1， YIN Xiaoyu2

(1. School of Electrical and Automation Engineering, East China Jiaotong University, Nanchang 330013, China; 2.Key Laboratory of Specialty Fiber Optics and Optical Access Networks, Shanghai University, Shanghai 200072, China)

Due to its simple algorithm structure, ease of performance, high optimization efficiency, simple parameter setting, and excellent robustness, the differential evolution (DE) algorithm has attracted increasing attention from researchers. In this paper, we outline the basic concepts of the DE algorithm as well as its limitations, and review four improvement strategies, including a control parameter, differential strategy, population structure, and mixing it with other optimization algorithms. We discuss the advantages and disadvantages of these strategies and suggest directions for future improvements to the DE algorithm.

differential evolution algorithm; heuristic parallel search; differential strategies; control parameter; population structure; mixed optimization; convergence rate; optimization efficiency

2016-05-17.网络出版日期2017-06-06.

国家自然科学基金项目(61501186)；江西省普通本科高校中青年教师发展计划访问学者专项资金项目；江西省自然科学基金项目(20171BAB202001)；江西省教育厅科学基金项目(GJJ150491).

丁青锋. E-mail：brandy724@sina.com.

10.11992/tis.201605015

http://kns.cnki.net/kcms/detail/23.1538.tp.20170606.1114.006.html

TP301

1673-4785(2017)04-0431-12

中文引用格式：丁青锋，尹晓宇.差分进化算法综述J.智能系统学报， 2017, 12(4): 431-442.

英文引用格式：DINGQingfeng，YINXiaoyu.ResearchsurveyofdifferentialevolutionalgorithmsJ.CAAItransactionsonintelligentsystems, 2017, 12(4): 431-442.