基于STL文件的3D打印分层算法
2017-12-22作者强邵雯西安市第八十三中学
作者/强邵雯,西安市第八十三中学
基于STL文件的3D打印分层算法
作者/强邵雯,西安市第八十三中学
目前,3D打印技术逐渐成熟,在日常用品、工业设计、建筑、医疗和教育等方面都有所应用。本文首先介绍了3D打印的基本原理及工作流程,分析了其误差来源并把重点放在对分层算法的研究上。本文选定基于STL文件的分层算法进行了更深入的研究。最后,对目前主流的分层算法进行了分析,介绍了一种基于分组排序的加权有向图递归分层算法。
3D打印;STL文件;分层算法
引言
当今世界,3D打印技术的出现和发展,有效地提高了产品开发和研究的效率,缩短了产品的开发时间,成为了企业间竞争成败的关键。因此这项技术的研发与优化受到了世界各地不同国家的广泛关注。3D打印具有成型快,产品精度高,生产过程无污染等优点,这也使得这项技术有着巨大的潜力和广阔的发展前景。所以对这项技术的研究及优化有着重大的意义[1]。
在进行3D打印时,我们最关心的性能指标主要是打印的精度,即实际打印出来的实物与模型的相似性。一般可以用体积误差来衡量3D打印产生的误差,即3D打印得到的实体所耗费的材料量与理论模型需要的材料量之间的差值。在进行3D打印时,主要会存在两种情况的误差。第一种可能存在的误差是在格式转换中产生的,即将CAD模型转化为STL标准格式文件过程中产生的误差;而第二种误差是阶梯效应,即在进行分层切片时,由于打印机能实现的最小打印厚度有限,造成的层与层之间所产生的误差[2]。
1. 3D打印分层算法
■1.1 分层算法简介
3D打印分层技术一般包括两个阶段,首先是获取模型与各层切平面交线段的集合,然后是将交线段进行首尾相连以获得封闭的轮廓环。一个模型文件中可能包括非常多的三角形面片,而且这些三角形面片的排列是无序、随机的,因此无论是计算交线段还是对交线段进行整理排序的效率都可能很低。由此可知主要有以下三点影响分层算法的速度:一是判断三角形面片与切平面的位置关系;二是求解面片与切平面的交线段;三是生成切平面的轮廓线。如何提高分层切片的效率是3D打印技术优化的重要问题,所以本文主要基于分层算法对如何提高打印时的效率进行研究。
■1.2 主流的3D打印分层算法
目前主流的分层算法主要包括以下几个类别:
(1)基于STL文件的分层算法:该方法首先将CAD模型转化为通用的STL格式,再对其进行分层处理,得到分层数据。这种方法的优点是格式简单,有统一标准,且实现的方式相对简单,成熟度较高等。但存在的主要缺点是对复杂模型,分层精度较低且耗时较长。
(2)基于CAD模型的分层算法:该方法跳过了转换为STL格式文件的步骤,直接对CAD模型进行分层处理,因此提高了效率。这种方法的一大优点是避免了在标准格式转换过程中引入的误差,因而提高了产品的精度。但缺点是缺乏统一标准,很难得到广泛的应用。
(3)基于点云数据的分层算法:该方法是通过现有的扫描技术先获取实体模型的点云数据,再根据该数据建立STL模型文件,在此基础上进行分层处理。通过这种算法所获得的模型精度较高,但其主要问题是实现难度很高且很难保证点云数据的正确性。
综上,本文选择基于STL文件的算法进行研究,主要因为它是一个主流的数据标准,具有较好的通用性,研究的算法可以很好地应用到大部分3D打印机上。另外该类算法的研究比较成熟,具有很好的研究基础,所以选择该类算法进行深入的研究[3]。
■1.3 几种基于STL文件的分层算法
STL文件是一种用若干个空间三角形面片来近似表示实体表面的数字格式文件。通过文件记录的各个三角形面片的顶点位置和法向量信息,即可恢复出与原实体高度相近的三维模型。一般而言,STL文件只保留实体名称、三角形面片的个数、各面片的顶点信息及法向量,所含的信息量虽少但足以满足实际的应用,其好处在于占用的内存小且可以保证应用的通用性。
STL模型需要遵循四大法则:一是右手法则,即每个三角形面片的法向量与其三个顶点的次序满足右手法则。二是定点法则,即模型中每两个三角形面片有且仅有两个顶点被共享。三是边法则,即模型中每一条边最多只能被两个三角形面片共享。四是面法则,即每个三角形面片有且仅有三个相邻的三角形面片。这四大法则很好地避免了分层算法在对面片进行交线段求解时重复性地对同一个对象进行运算。
以下介绍主流的基于STL文件的分层算法[4]。
1.3.1 直接求交线的分层算法
该算法分层时首先通过预先的计算,确定一个最优分层方向,目的是尽量减少分层后所产生的体积误差。然后确定分层高度的最小值及最大值并确定分层厚度。在设定当前分层高度为最小值后,遍历所有三角形面片,判断各面片顶点与当前平面的位置关系。根据位置关系,对与当前分层切面有交线的面片进行交线段求解运算,得到三角形面片与切平面的两个交点。再根据三角形之间的位置关系判断交线的顺序,连接各个交线,形成闭合的轮廓环,得到该模型在当前高度的截面轮廓。接着逐层提高分层切面的高度,重复以上步骤,直至超过该模型的最大高度,即完成了该模型的分层过程。
1.3.2 基于模型毗邻拓扑信息的分层算法
该算法首先读取STL模型信息,并对所有三角形面片进行预处理,得到模型的毗邻拓补信息。然后开始分层,先寻找首个与当前切平面相交的面片,进行求交点的运算,得到交线段。再根据之前建立的拓扑信息,得到与其相邻的面片地址,再选择该临近面片进行求交点的运算,并不断往下追踪,最终得到与该切平面相交的所有交线段,然后根据它们的顺序连接成轮廓环。这种方法的优点是每个交点的计算只有一次,且提前获取了毗邻拓扑信息,在生成轮廓线时则无需再判断各个交线段的位置关系,效率可大大提高。但需提前建立整个模型的拓扑信息,该过程较为复杂且难度高,对内存的消耗大,且十分耗时。
■1.4 基于分组排序的加权有向图递归分层算法
基于分组排序的算法的实现难度、效率及复杂度相对于其他算法具有很大的优势。本文在分组排序的基础上,利用加权有向图的概念,结合递归搜索的算法思想,实现了一种快速高效的分层切片算法。以下针对算法实现过程进行具体的介绍。
1.4.1 分层矩阵的建立
假设当前切平面i高度为Z[i],当前访问的面片j在分层方向的最大值为Zmax[j]最小值为Zmin[j];设分层厚度为为ZΔ,最小值为Zmin[j],则与该切平面相交的最低切平面m和最高切平面 n分别为:
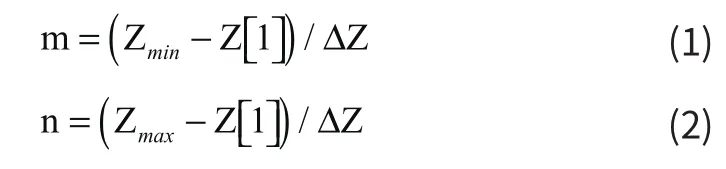
由上式则确定了与面片j相交的所有分层切面的序号,并可根据m值的大小将面片放入对应的分层矩阵中。注意到如果满足ZmaxminZ= ,则表明该三角形面片与切片方向垂直,与切平面不会有交点,可以把它删除,不放进分层矩阵中。
1.4.2 基于STL的加权有向图数据结构建立
由于加权有向图能很好的表示点与边的位置关系,因此本文将其应用到分组排序的分层算法中,以表示活性面片表中所有面片的局部拓扑信息。其主要过程为:首先为活性面片表的每个三角形面片赋予唯一的编号ID(0,1,2,3,…,N),并把它们近似为图上的一个点。然后根据面片的相邻关系,在相邻的两个面片近似成的顶点间连接一条有向边,从而建立一个有向图。为每条有向边赋予不同的权值,形成加权有向图,因此得以反映模型的局部拓扑信息。将加权有向图用“邻接表”的数据格式进行表示,并将其添加到原STL格式的每个三角形面片的数据结构中,形成具有拓扑信息的数据,便可储存于计算机上[5]。
2.结论
当今时代3D打印正在飞速发展,对该技术的不断优化与创新也成为了在市场竞争中的重要因素之一。本文通过对几种传统方法的学习,在此基础上利用加权有向图和递归搜索的思想,提出了一种新的优化的算法方案,提高了分层的效率。3D打印是目前乃至将来都很有发展前景的一项工程,在今后的研究中,优化、创新出新的算法方法对于人类科学的进步、世界的进步都有着毋庸置疑的重要作用。
* [1]刘红霞,3D打印分层方向优化与分层算法研究[M], 西安电子科技大学, 2014
* [2]杨猛,3D打印驱动电路设计及文件切片算法研究[M],北京印刷学院,2015
* [3]赵方,3D打印中基于STL文件的分层算法比较[M],大连理工大学,2016
* [4]罗中明,3D打印算法研究及应用[M],北京印刷学院,2014
* [5]卢凯,基于FSM的3D打印分层处理技术研究[M],长春工业大学,2015
