船体极限强度非线性有限元计算方法

伍友军，万 琪，周 博

（中国船舶及海洋工程设计研究院，上海 200011）

船体极限强度非线性有限元计算方法

伍友军，万 琪，周 博

（中国船舶及海洋工程设计研究院，上海 200011）

船体极限强度是关系到船体生命力和安全的重要指标之一，各国规范都对其提出明确要求。以某双壳油船为研究对象，采用非线性有限元法计算其极限承载能力。通过采用不同的网格尺寸、边界条件、加载方式及施加或不施加侧向载荷，对同一对象进行有限元计算。对计算结果进行对比分析，提出合适的网格尺寸、边界条件设置方式和加载方式，同时得出施加侧向载荷及不施加侧向载荷的优缺点。该研究可为采用非线性有限元法计算船体结构极限强度提供参考。

非线性有限元；极限强度；船体结构

0 引 言

船体极限强度分析是船体结构强度分析的重要内容之一，关系到船舶的安全运营。船体总纵极限强度[1]是指船体抵抗纵向整体崩溃的最大能力，是评估船体结构在特殊装载状态或恶劣海况下的安全性的重要指标。对船体结构的极限强度进行分析能准确把握船体的实际承载能力，为进一步优化构件尺寸、提高船舶的经济效益提供依据[2]。目前，相关规范[3-4]推荐采用渐进崩溃法（Smith方法）计算船体的极限强度，进行船体极限强度评估，同时认可采用非线性有限元法替代Smith法。劳氏军规在剩余强度三级评估(RSA3)中明确要求需采用有限元法计算破损船舶的极限承载能力。

船体结构是一个由纵横方向上设置加强筋的加筋板组成的三维结构，随着对船体发生极限强度破坏的崩溃机理的研究不断深入，人们逐渐认识到船体结构在外载荷作用下达到极限状态是一个伴随着构件遭到破坏和应力重新分布的过程，包含构件的后屈曲行为、几何大变形和材料的非线性应力-应变关系等复杂的力学响应过程。相较于渐进崩溃法，非线性有限元方法是一种能反映船体构件局部破坏模式与整体破坏模式之间的相互作用，计及几何、材料及边界非线性因素，模拟船体发生整体崩溃全过程的计算方法[5]。通过大量计算发现，在采用非线性有限元方法计算极限强度时，单元网格大小、边界条件和加载方式等因素会对计算结果产生较大的影响，需通过对不同参数下的计算结果进行对比分析，为极限强度的计算分析提供一种较为合理的方法，从而使得采用有限元法计算极限强度更加规范、高效和准确[6]。

1 单元网格大小的影响

采用非线性有限元方法计算极限强度是基于有限元模型进行的，有限元模型的质量直接影响计算结果的准确性。在将实际的船体结构抽象为适合计算机求解的有限元模型时，需针对不同的研究内容合理地选择网格划分技术，合适的网格尺寸应是在综合考虑计算精度和计算成本的基础上得到的。更加细化的网格有助于更加敏感地捕捉到构件局部产生的屈曲现象，但会增加计算成本。通过分析比较发现，过密的网格划分不会对计算结果产生明显影响，但会使计算代价大大提高。本文对同一船体结构建立1肋位、1/2肋位和1/4肋位单元网格大小的模型，在相同的边界条件和相同的载荷加载方式下模拟中拱状态的极限强度破坏，计算模型见图1，3种不同网格尺寸模型的极限弯矩计算结果比较见表1。

表1 3种不同网格尺寸模型的极限弯矩计算结果比较

对比3种不同单元网格大小的计算模型可知，单元网格的大小对加筋板的屈曲破坏模式有很大影响，内底板架的屈曲模式见图2～图4。从3种模型分别处于极限状态时的破坏模式中可看出：对于单元网格较大的1肋位模型，当其发生极限强度破坏时，内底加筋板格的破坏模式属于加强筋与板格同时发生屈曲失稳破坏的梁-柱破坏模式；对于单元网格较小的1/2肋位模型和1/4肋位模型，当其发生极限强度破坏时，内底加筋板格的破坏模式属于加强筋之间的板格屈曲失稳引起整体板格失稳的破坏模式。

加筋板板格基本上可按总体屈曲和局部屈曲2种方式屈曲。通过理论计算发现，由于目标船型船底结构的加筋板板格发生总体屈曲的应力要比板格屈曲的应力大，较大的单元网格无法反映构件的局部破坏模式。通过对比发现，单元网格的大小会直接影响船体结构关键区域的破坏模式，导致计算结果出现较大偏差。采用1肋位单元网格无法反映构件的局部破坏模式，而采用1/4肋位单元网格对提高计算精度的作用较小且会增加计算成本，因此推荐采用1/2肋位单元网格建立有限元模型。

2 边界条件的影响

目前在采用非线性有限元法分析船体结构极限承载能力时，有采用无延伸段和有延伸段加载及施加边界条件2种方式。分别在3种单元网格大小和2种加载方式条件下对2种计算模型进行计算。对于没有延伸段的模型，其边界条件和载荷均直接作用在框架模型的两端。对于有延伸段的模型，其两端各延伸出1个强框架的长度，并对延伸段的板厚进行加厚处理，保证破坏发生在中间核心段。有延伸段模型和无延伸段模型见图5，计算结果对比见表2。

表2 2种模型计算结果对比

通过对计算结果分析可知：对于无延伸段模型，按不同的加载方式在3种单元网格大小条件下所得计算结果的差值离散性较大，而在相同的单元网格大小条件下，不同的加载方式会对模型的计算结果产生影响；有延伸段模型在3种单元网格大小条件下的极限弯矩值的差值离散性较稳定，同时在相同的单元网格大小条件下，不同的加载方式对模型的极限弯矩值没有明显影响。将有延伸段模型作为计算船体局部框架极限强度的模型是更加符合实际情况的处理手段，能得到更为准确的计算结果。

当计算模型选取两个相邻横框架之间的结构时，在原有计算模型的两侧增加用于施加载荷和边界条件的延伸段，并增加延伸段的板厚，保证整体崩溃发生在所关注的原横框架之间，这种方法能更好地模拟实际情况，降低边界条件的影响。在相同网格大小和相同加载方式的有限元模型两端，采用2种不同的边界条件（见表3），计算结果见表4，相应边界条件下的极限强度破坏模式见图6和图7。

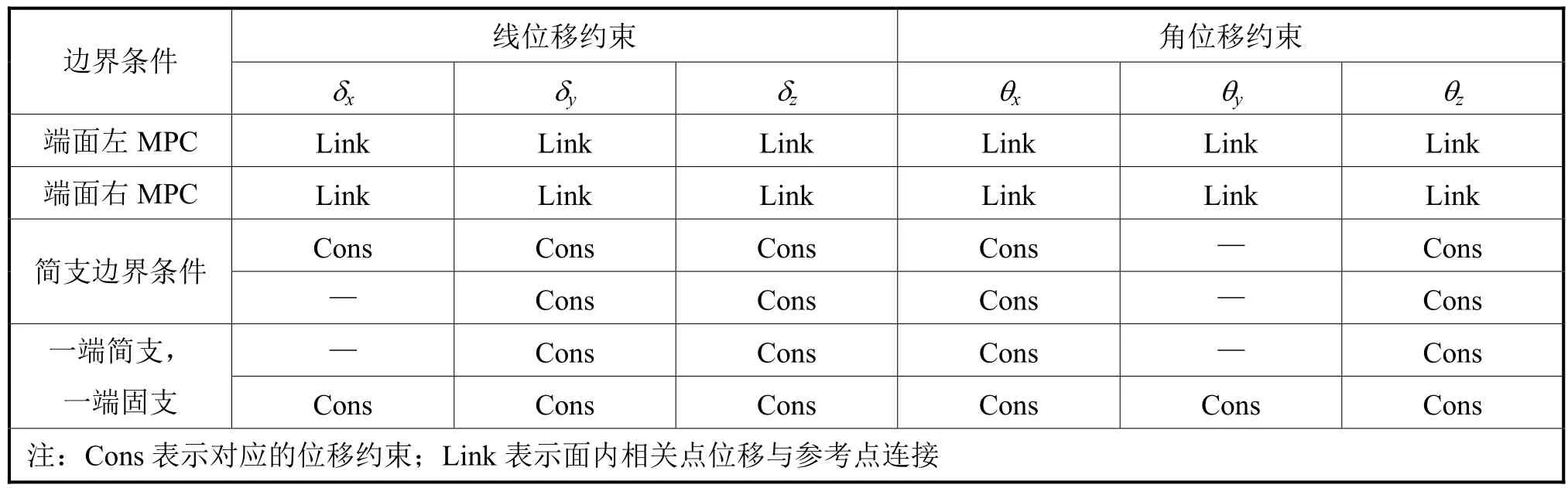
表3 端面2种边界条件

表4 2种边界条件计算结果

对比2种不同边界条件的计算结果可发现，由于延伸段的存在，模型中间核心段的极限弯矩值及其相应极限状态下的破坏模式基本一致，采用在有限元模型两侧增加延伸段的方法能有效消除边界条件对计算结果的影响，使所关注区域结构的极限强度计算结果更接近于实船。在采用核心段两侧加延伸段的方式之后，两侧边界条件采用简支或一端简支一端固支均可。

3 加载方式的影响

弧长法是增量非线性有限元分析中的一种由弧长控制，在包含真实平衡路径的增量位移空间中利用Newton-Raphson迭代方法自动确定各增量步中满足力平衡方程的增量大小和加载方向的高级非线性追踪方法。在增量加载分析中，加载方式可分为按载荷控制的加载和按位移控制的加载2种。对具有延伸段的1/2肋位模型分别采用按载荷控制的加载方式和按位移控制的加载方式进行极限弯矩的计算。

载荷控制方法是在一组给定的节点载荷增量下求解与其相应的节点位移增量；要顺利计算得到目标结构的极限承载能力，需经过多次试算来确定加载历程中的平衡路径。针对有延伸段的1/2肋位模型，采用按载荷控制的加载方式，采用简支约束条件，向左右端面施加初始弯矩载荷选取5个典型的载荷增量步进行极限弯矩值的计算，计算结果见表5和图8。

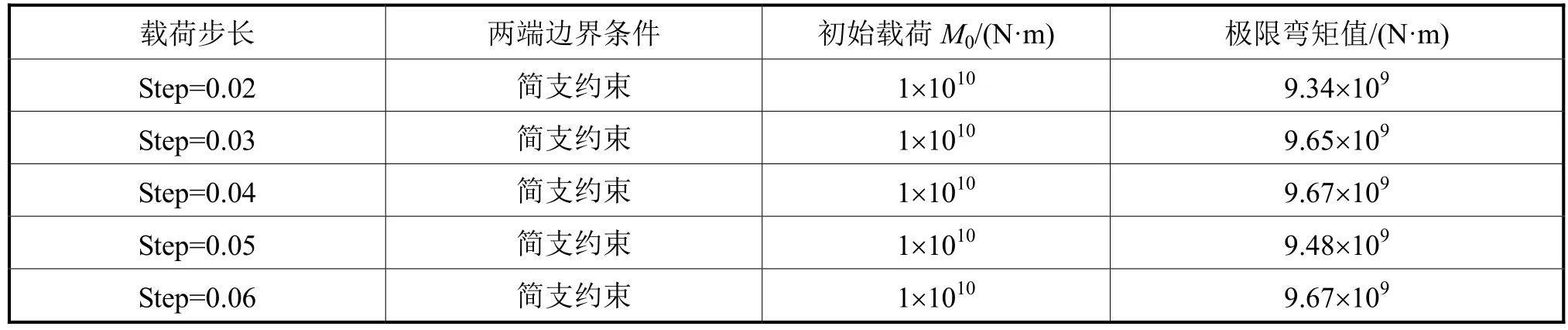
表5 载荷控制加载方式计算结果

从计算结果中可看出，在相同的初始载荷和边界条件下，选取不同的初始载荷步长会对极限弯矩值的计算产生较大影响，且不同的初始载荷步长有着显著的收敛性差异。某些初始载荷步长能平稳地接近或通过极限载荷峰值点，而某些初始载荷步长则无法准确计算出极限载荷，整个加载历程的平衡路径不稳定，这可归因于在某些增量步的迭代过程中收敛性较差。

采用与按载荷控制的加载方式相同的有延伸段的 1/2肋位单元网格模型，在模型的一端施加转角位移，在其另一端施加固支约束，通过计算固定端的反作用弯矩来确定整个模型中各转角位移下的弯矩值。计算结果见表6和图9。

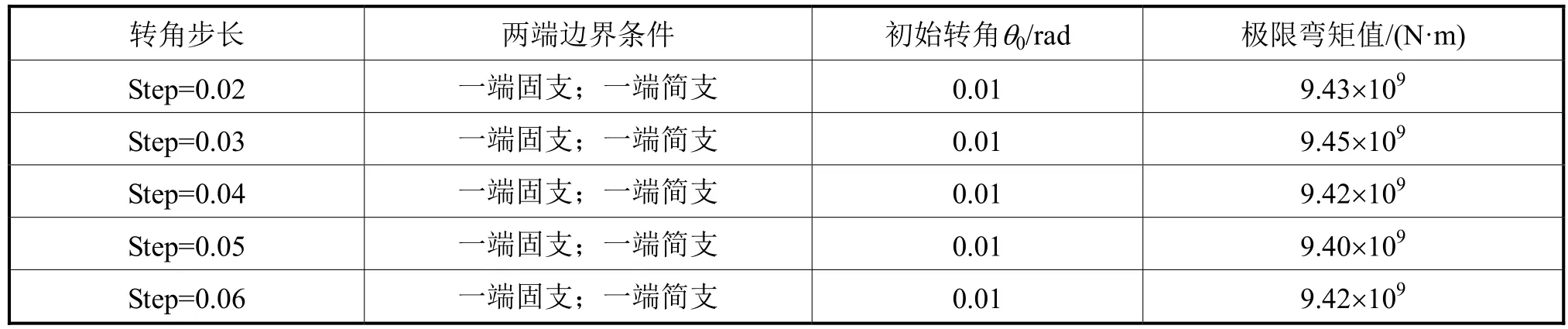
表6 位移控制加载方式计算结果

从计算结果中可看出，在采用按位移控制的加载方式时，不同初始载荷步长下的极限弯矩的计算值都非常接近，且每个初始载荷步长都能平衡、顺利地逼近结构载荷-位移曲线的峰值，几条加载曲线所经历的结构的平衡路径基本上是吻合的。

通过比较分析可知，在结构形式复杂的情况下，采用按载荷控制的加载方式计算需具有丰富的计算经验，否则需经过多次试算，计算效率较低。采用按位移控制的加载方式计算得到的结果离散程度较小，计算效率较高，推荐采用该方式进行计算。

4 侧向载荷的影响

船体梁载荷分为静水载荷和波浪载荷，船体的极限破

坏过程为船体在静水载荷下具有一个初始状态，在此基础

上叠加恶劣波浪载荷直至船体遭到破坏，此时对应的极限载荷可认为是船体的极限承载能力。船体梁在不同载荷形式下的极限承载能力会有差异，实际采用非线性有限元法计算极限弯矩时，有不施加静水载荷而直接在舱段端部增加转角（这种方式比较简便）和施加静水载荷后在舱段端部增加转角2种加载方式。选取目标船典型的舱段建立有限元模型，分别采用施加静水载荷和不施加静水载荷2种方式进行计算，静水载荷采用散货船和油船共同结构规范（Common Structural Rules，CSR）舱段强度分析中的加载方式加载，此处不再详细描述静水载荷的施加过程，计算选取一个舱长范围的舱段，舱段有限元模型见图10，内外壳侧向载荷施加模型见图11，2种加载方式模型计算结果见表7。

表7 2种加载方式模型计算结果

相对于施加侧向载荷的舱段模型，纯舱段结构模型的计算由于不必考虑静水载荷的影响，计算过程比较简便，但计算结果偏大，只能反映出船体结构在纯弯情况下的极限承载能力，没有计及实际船舶在不同装载条件下的静水载荷对船体结构中应力分布的影响。此外，纯舱段结构在极限状态下的破坏位置也会与实际情况有差别。由于实际舱段结构的薄弱剖面的位置不仅与船体结构有关，而且会在不同载荷分布（局部载荷）的作用下发生变化，因此有可能导致纯舱段结构模型发生极限状态破坏的位置与实际情况不同，这会对运用非线性有限元方法预报实船的极限强度大小和破坏模式产生不利影响。在考虑静水载荷的影响后，有限元模型舱段与实船舱段在相同的装载工况下具有近似的静水载荷分布，能较为真实地模拟实船的初始变形和初始应力分布。在此基础上，舱段的极限强度计算结果的可靠性和准确性更高，计算结果相对安全。

5 结 语

通过采用非线性有限元法对目标船型的极限承载能力进行计算，比较不同的单元网格大小、边界条件、加载方式和侧向载荷对计算结果的影响，结果表明：1) 综合考虑计算精度和计算时间，网格尺寸取为1/2肋距大小时，能以合适的时间代价得到足够精确的计算结果，是相对最优的选择；

2) 由于采用在校核剖面增加延伸段的方法时，边界条件对计算结果的影响较小，端部采用简支和固支方式均可；

3) 采用按位移控制的加载方式能更好地追踪极限弯矩的最高点，相较于按载荷控制的加载方式有一定的优越性；

4) 采用考虑侧向载荷的舱段分析方法能得到相对更准确的极限承载能力，但加载方式复杂，目前规范衡准对应的是不施加侧向载荷的计算方法。

[1]卢润泽. 舰船总纵弯曲极限承载能力[M]. 哈尔滨：哈尔滨工程大学，2012.

[2]王峰，陈毓珍，张青敏. 全船有限元简化方法在总纵强度计算[J]. 船舶与海洋工程，2014 (1): 24-27.

[3]DNV-GL. DNV GL rules for classification [S]. 2015.

[4]IACS. Common structural rules for bulk carriers and oil tankers[S]. 2015.

[5]郑牡丹，卢俊峰，赵耀. 非线性有限元计算船体总纵极限强度浅析[J]. 中国水运，2007 (2): 130-131.

[6]汤红霞，王晓宇，刘见华，等. 舰船极限强度计算及试验研究[J]. 船舶，2014 (3): 26-29.

Research on the Nonlinear Finite Element Method for Ultimate Strength of Ship Hulls

WU You-jun，WAN Qi，ZHOU Bo

（Marine Design & Research Institute of China, Shanghai 200011, China）

The ultimate strength of ship hulls is one of the important factors for ship vitality, the requirements on which are clearly specified in the rules and regulations of classification societies around the world. Taking a double hull oil tanker as the research object, the nonlinear finite element method is adopted to calculate its ultimate strength. Finite element calculations on the same object are performed with different gird sizes, boundary conditions, loading modes and with or without lateral loads. The calculation results are compared and analyzed to propose the proper grid size, boundary condition configuration and loading mode, and to obtain the advantages and disadvantages of whether or not to apply the lateral loads. This study can provide some reference for the hull structure ultimate strength calculations using nonlinear finite element method.

nonlinear finite element; ultimate strength; hull structure

U661.43

A

2095-4069 (2017) 06-0020-06

2016-11-15

伍友军，男，高级工程师，1980年生。2002年毕业于上海交通大学船舶与海洋工程专业，现从事船舶结构设计工作。