Matlab 在几何光学仿真实验中的应用
2017-12-21冯东太
秦 华, 冯东太
(山东理工大学 理学院,山东 淄博 255049)
普通物理实验
Matlab在几何光学仿真实验中的应用
秦 华, 冯东太
(山东理工大学 理学院,山东 淄博 255049)
在工程光学教学中,为了使学生更好地理解球面光学成像系统与理想光学成像系统的区别,提出了用Matlab程序模拟球面光学系统成像过程的仿真实验,并编制了模拟程序. 把系统结构参量r,d,n和物距L等代入到模拟程序中,就可以仿真成像系统的成像过程. 仿真实验结果显示:理想光学成像系统的成像性质在球面光学成像系统中不存在,但可以通过设计优化使球面系统近似达到或者无限接近理想成像系统,理想成像系统的意义在于它的标准性.
几何光学;理想光学成像系统;球面光学成像系统;计算机仿真
研究光学系统的成像问题是几何光学的主要内容, 目前所使用的成像系统一般是球面镜成像系统,也有的在球面系统中加入1~2个非球面[1-2],还有一些加入部分二元光学元件[3],这些都还是以球面成像系统为基础.
在工程光学教学中,德国科学家高斯在1841年提出了理想光学系统的概念. 实际中除平面反射镜外不存在真正的理想光学系统,但平面反射镜的垂轴放大率是1且成虚像,不适用于成像记录. 理想光学系统中把光离散成光线,变成了纯粹的几何理论. 在工程光学教材中[4], 理想光学系统有下列3条重要性质:
1)光学系统物方1个点(物点)对应像方1个点(像点),即从物点发出的所有入射光线经光学系统后,出射光线均交于像点.
2)物方每条直线对应像方的1条直线,称共轭线;物方每个平面对应像方的1个平面,称为共轭面;任何垂直于主光轴的平面,其共轭面仍与主光轴垂直.
3)对垂直于主光轴的共轭平面,垂轴放大率为常量.
这3条性质对于球面光学系统远轴光束不成立,或者只能近似成立. 由于学生还没有接触到光学设计,对此学生很难理解,教师在课堂上也不容易讲明,对此可以使用光学CAD来演示讲解这个问题. 但是光学CAD都是商业软件,使用需要一定的基础,再者即使会使用也无法展示其产生现象的原因. 而Matlab作为一种高级编程语言,由于其语法规则简单,贴近于人的思维方式,具有建模和仿真等诸多强大功能[5],因此可以引入到工程光学实验教学课堂中,让学生自己编程仿真光线在光学系统中的传播过程,通过仿真结果理解理想光学系统的3条性质,从而知道这3条性质的意义就是作为一种设计标准而存在.
1 实际光线的光路计算及仿真
单个折射面的光路公式为[4]
(1)
式中,I和I′分别是入射角和折射角,n和n′是折射面两侧介质折射率,r是球面的曲率半径. 由式(1)可知,若物方截距L和物方孔径角U已知,可以求得像方截距L′和像方孔径角U′. 式(1)由折射定律和几何三角关系得到,属于实际光路的计算公式,是正确的,所以根据式(1)所编仿真程序的仿真结果也是正确的. 若有多个折射面,可迭次用式(1)和前后面的过渡公式(2)逐面计算.
(2)
因此可以用式(1)和(2)逐个验证理想光学系统的3条性质. 为此开设了仿真实验课,让学生自己编写Matlab仿真程序,模拟光束在光学系统中的传播过程.
1.1 光学系统物方1个点(物点)对应像方1个点(像点)的模拟证伪
表1列出了其双胶合物镜的结构参量,选择物距l=-75 mm,数值孔径sinUmax=0.105,入瞳距lz=0,物高y=-7 mm.
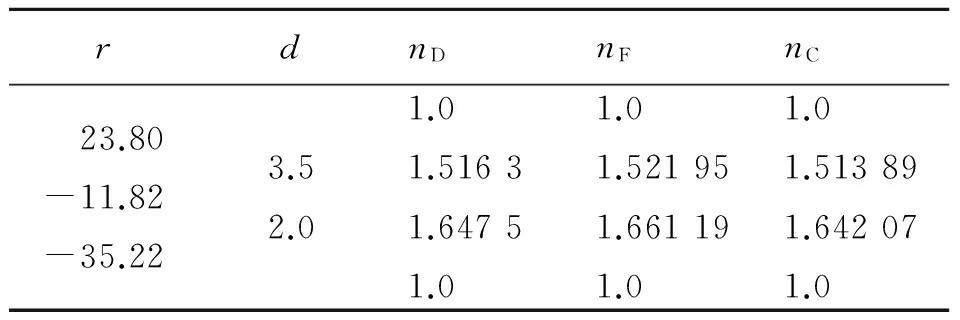
表1 物点对应像点的模拟结构参量
根据式(1)和(2)用Matlab语言编制光从物点经过物镜到像点的光线传输程序如下:
r=[23.8,-11.82,-35.22];
n=[1.0,1.5163,1.6475,1.0];
L(1)=-75;d=[3.5,2.0];
k=length(r)
for m=1∶k
n′(m)=n(m+1);
I(m)= asin((L(m)-r(m))*sin(U(m))/r(m));
h(m)=r(m)*sin(U(m)+I(m));
I′(m)=asin(n(m)/n′(m)*sin(I(m)));
U′(m)=U(m)+I(m)- I′(m);
L′(m)=r(m)*(1+sin(I′(m))/sin(U′(m)));
x(m)= L′(m)- r(m)*cos( I′(m)+ U′(m));
y(m)= r(m)*sin( I′(m)+ U′(m));
if m==1
dist=0;
else
dist=d(m-1);
end
b=dist+b;
if m==k
break
end
U(m+1)= U′(m);
L(m+1)=L′(m)-d(m);
end
plot(x,y)
此程序比较简单,通过引导,大部分学生都会编写,其中的意义也比较容易理解,所以通过程序的运行,学生肯定对于“理想光学系统物方1个点(物点)对应像方1个点(像点)”这条性质的理想性有深刻的理解. 图1 是以上程序的运行结果,从图中可以看出,物平面上的3点只有中间物点近似对应1个像点,其余两物点经过物镜后变为散斑,说明这个物镜不是理想成像系统. 要想成为或者近似成为理想成像系统必须对系统进行优化设计,才能在一定成像范围内近似达到“理想光学系统物方1个点对应像方1个点”,这属于光学设计范畴,在此不予赘述.
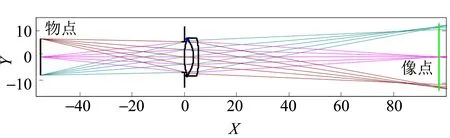
图1 物点对应像的仿真模拟
1.2 物方每条直线对应像方的1条直线,称共轭线的模拟证伪
表2给出了另一光学系统的结构参量,选择物距l=-1 mm,物空间数值孔径sinUmax=0.100 305 6,孔径光阑位置位于第4面顶点,物高y=-3.5 mm. 在物面上取3个点A,B和C,A是轴上点,B和C是轴外的2个物点,同样可以根据式(1)和(2)编程模拟A,B和C3个点发出的光经过此光学系统后的成像情况,模拟结果如图2所示. 从图2可以看出,A,B,C3个点的像点分别为A′,B′,C′,在物空间ABC成1条垂轴直线,但ABC的像A′B′C′与光轴不再垂直,也不在1条直线上,说明“物方每条直线对应像方的1
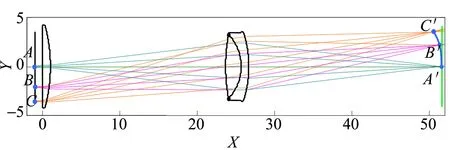
图2 物距有限远时共轭线的仿真模拟
条直线”对于一般光学系统的不真实性. 由于以上系统中物方每条直线成像后并不是1条直线,所以也谈不上“物方每个平面对应像方的1个平面”. 从图2所示的现象可以引出像场弯曲的概念,也就是像差理论中的场曲,为工程光学后章节像差理论的学习打下基础.
从以上分析中还可以引导学生理解理想光学系统的重要性. 如果不是理想光学系统,所成的像就要变形,变形后像就失去了存在的意义,这样的光学系统在市场就失去了竞争力.
图3是一成像物镜对于无穷远处的物成像模拟光路图. 从图3中可以看出,对于无穷远处轴上物点发出的11条光线,经过光学系统后还能很好地聚焦在一点(像点),但是对于无穷远处轴外物点发出的11条光线,经过光学系统后只能近似地聚焦在一点(像点),并且这个轴外像点与轴上像点不在同一条垂轴线上,即垂直于主光轴的直线成像后不再垂直于主光轴,像场也发生了弯曲. 这与理想光学系统 “任何垂直于主光轴的平面,其共轭面仍与主光轴垂直” 的性质明显不符.
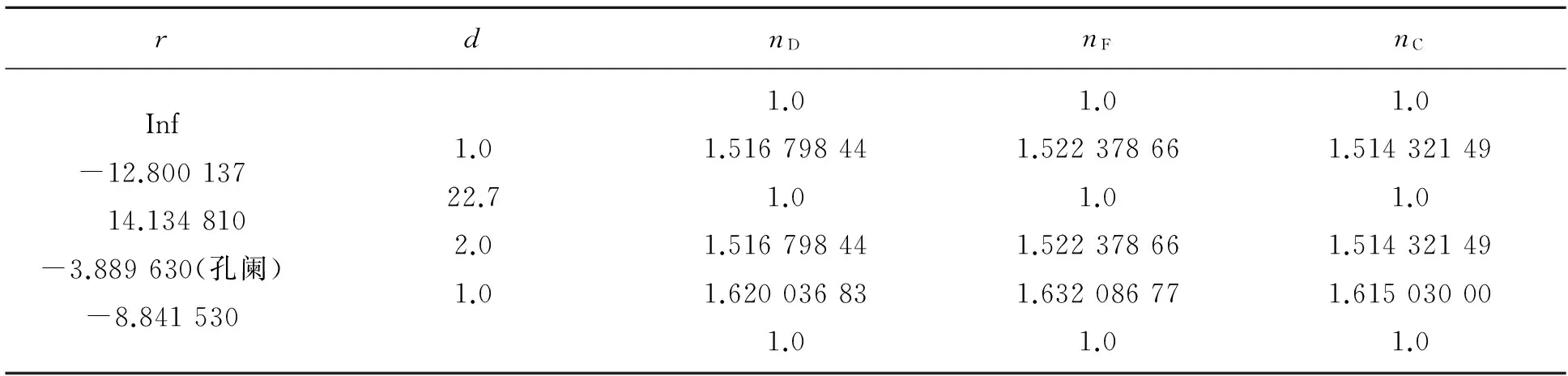
表2 共轭线的模拟结构参量
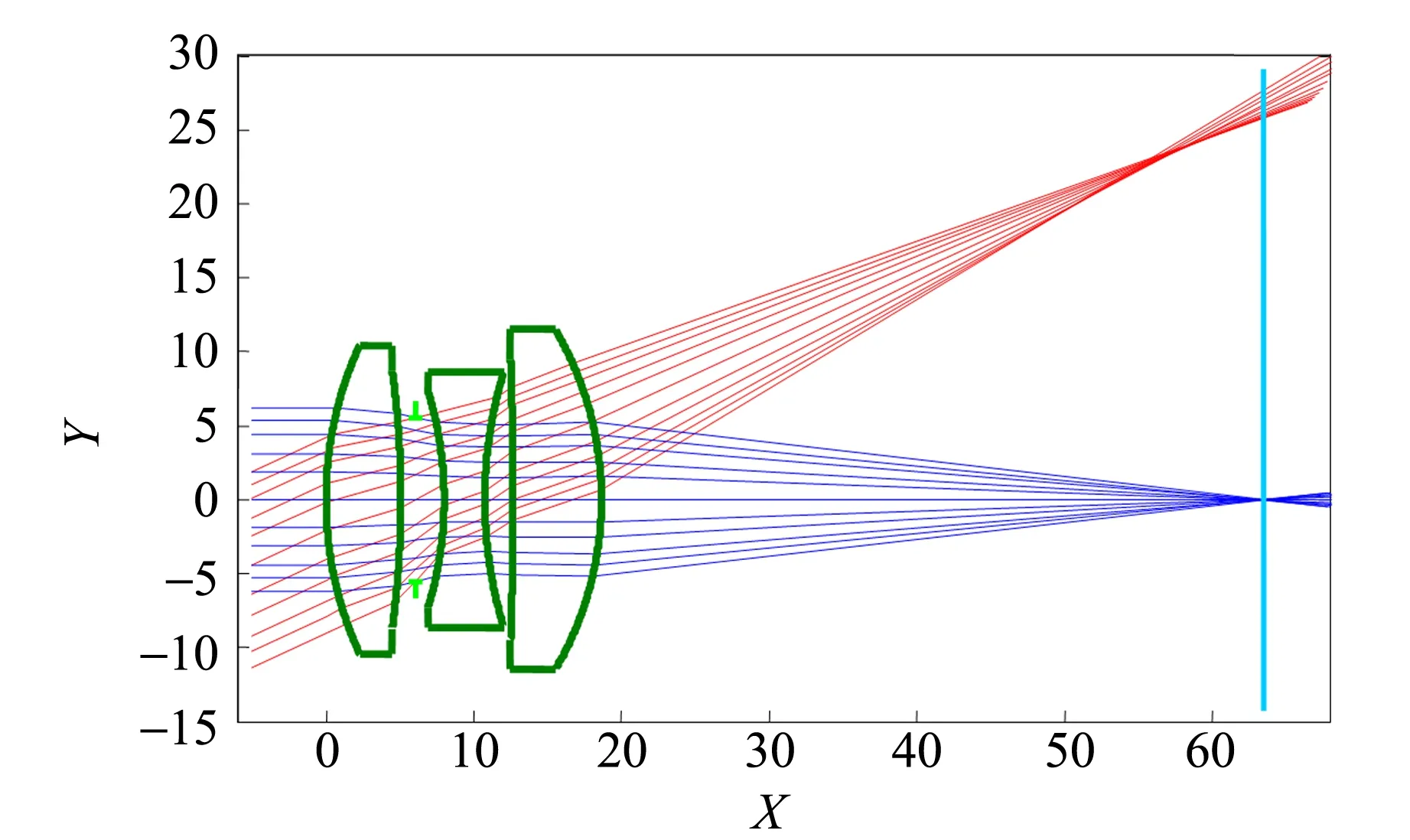
图3 物距无穷远时光学系统的成像模拟
为了达到或近似达到理想光学系统所具有的性质“物方每条直线对应像方的1条直线,任何垂直于主光轴的平面,其共轭面仍与主光轴垂直”,就必须对该光学系统的结构参量r,d,n进行调整优化. 优化的方法很多,现在光学设计最常用的是最小二乘法,如ZEMAX,CODEV,OSLO等,文献[6-7]用粒子群算法进行光学系统结构优化和设计,取得了理想的效果. 由于本科生刚刚接触到工程光学,对像差理论还不了解,所以还不能进行光学系统设计和优化, 教师可以直接把优化
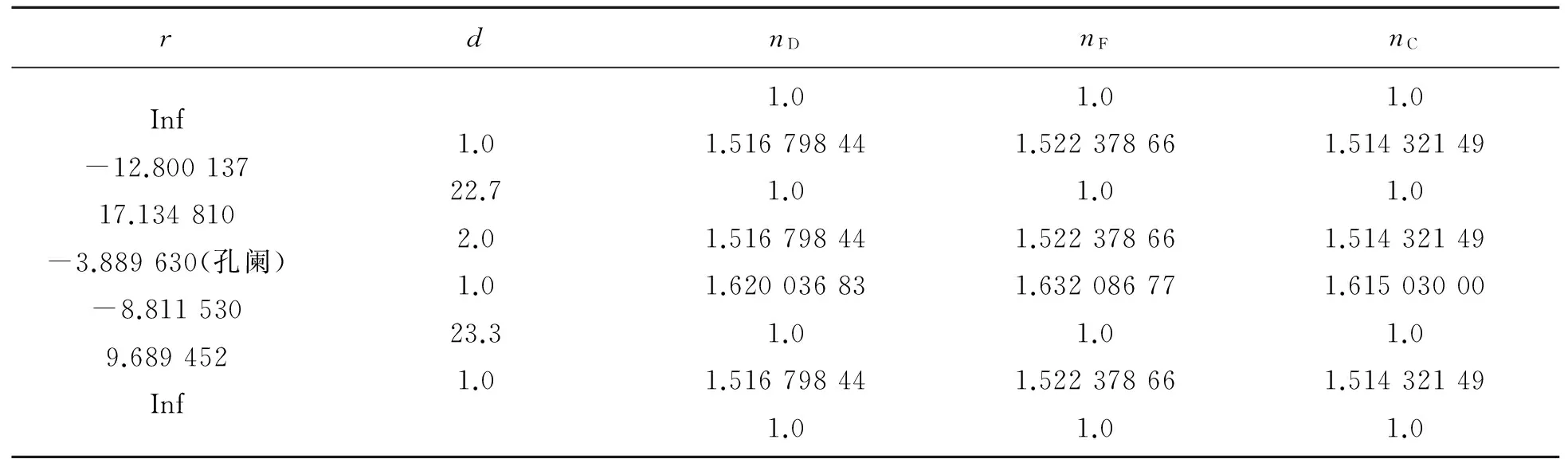
表3 优化共轭线的模拟结构参量
结果提供给学生,让学生由优化得到的系统结构参量进行光学模拟,从模拟结果对比优化前后的不同. 表3给出了在表2所给结构的基础上进一步消除场曲的新结构参量,物距l=-1 mm,物空间数值孔径sinUmax=0.100 005 6,孔径光阑位置位于第4面顶点,物高y=-2.5 mm. 图4是由表3中结构参量模拟得到的二维光路图,从中可以看出垂直于光轴的物AB经此光学系统后像A′B′近似垂直于光轴,说明表3中的光学系统在一定成像范围内近似满足理想光学系统“物方每条直线对应像方的1条直线”的性质. 从这里也可以引导学生懂得学习工程光学的最终目的是培养光学设计工程师,研究光学设计的方法,使所设
计的成像系统无限接近理想成像系统.
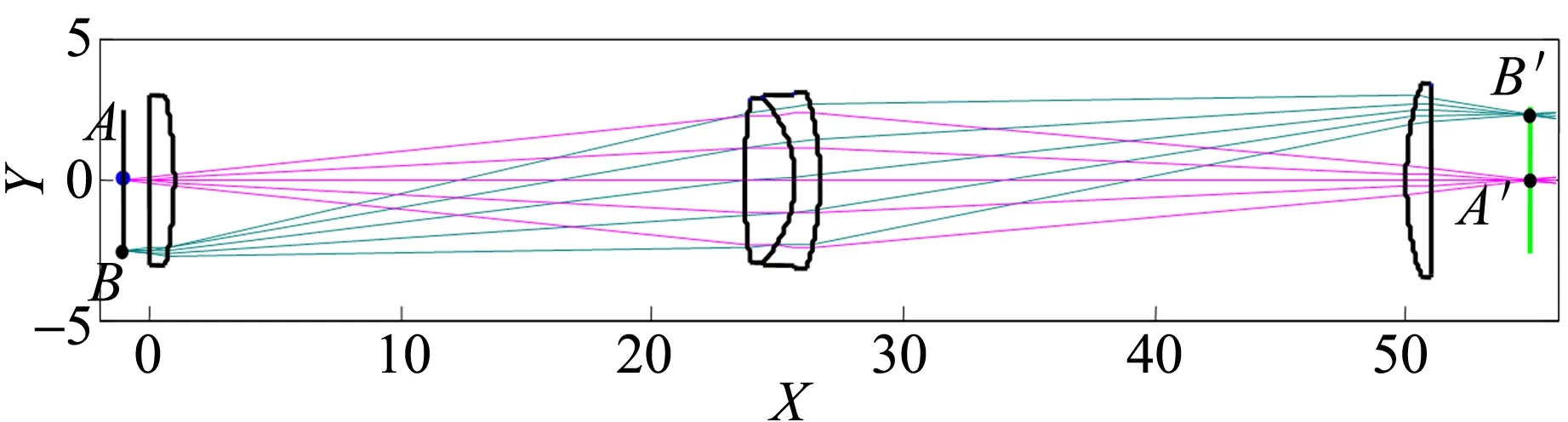
图4 优化后的共轭线的仿真模拟
1.3 对垂直于主光轴的共轭平面,垂轴放大率为常量的模拟证伪
表4列出了由ZEBASE库中搜到一光学系统的结构参量,物距l=-315.189 9 mm,物空间数值孔径sinUmax=0.019 628 58,孔径光阑表4中已给出,成像最大物高y=-80 mm.
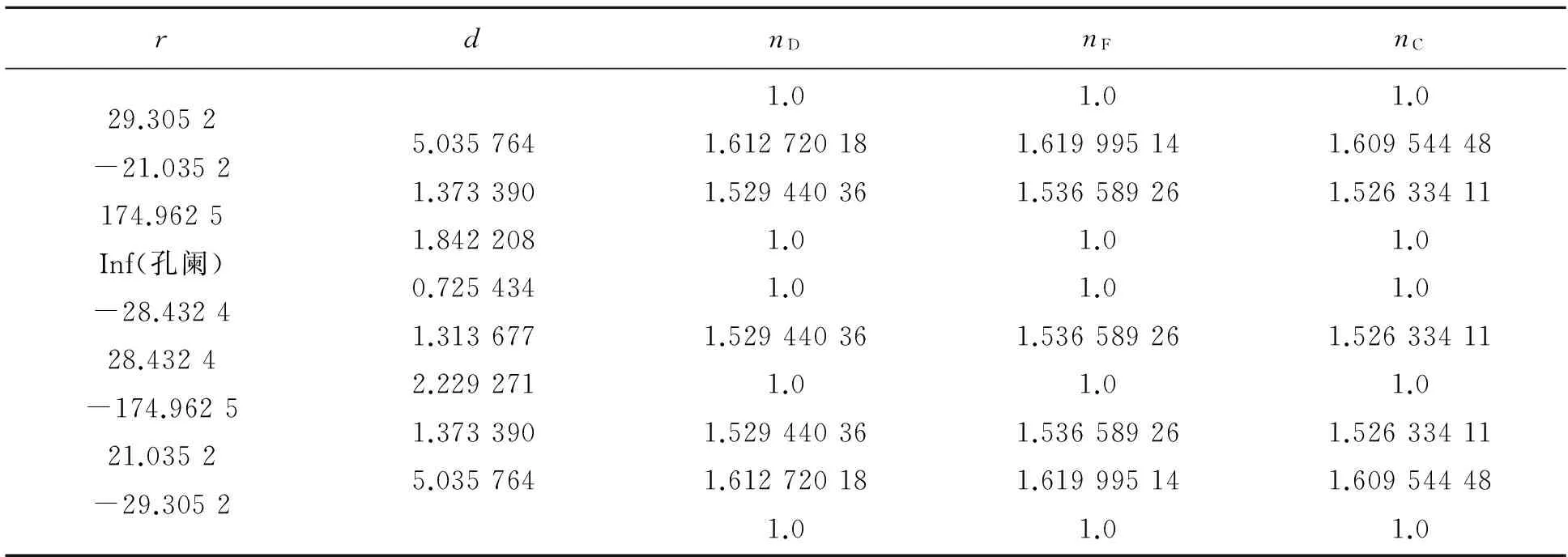
表4 由ZEBASE库中得到的共轭面模拟结构参量
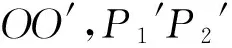
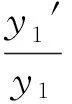
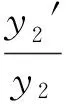
显然,β1≠β2,说明系统垂轴放大率并不是常数,此系统不是理想系统,但就其垂轴放大率来讲已经非常接近理想光学系统. 使垂轴放大率是一常数,达到理想成像系统,是光学设计工作者一项重要的研究内容.
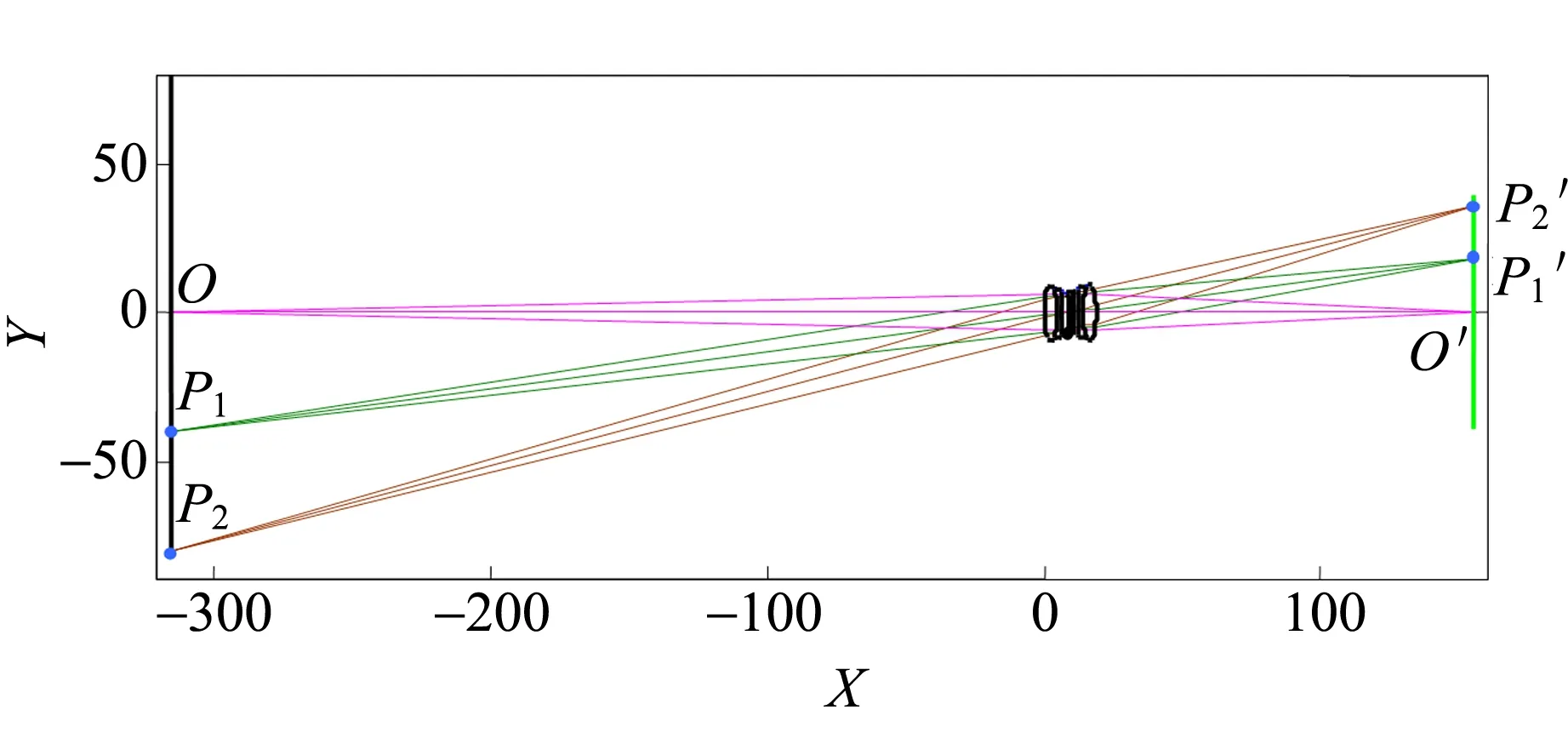
图5 共轭面的仿真模拟
2 讨 论
目前只有平面镜能达到理想光学系统的要求,但平面镜的放大率为1,所成的像为虚像,因此不适用于记录真实世界. 现在常用的光学成像系统大多是球面成像系统,对于球面成像系统与理想成像系统的区别,学生很难理解,认为工程光学中所讲的理想光学成像系统的成像公式是任何光学成像系统都适用的,这种误解导致了工程光学学习中概念的混乱. 本文根据几何光学理论,从学生熟知的球面折射公式出发,使用Matlab语言编程仿真了球面光学系统成像过程,由仿真结果证实理想光学系统所具有的性质对于球面光学系统是不存在的,起码不能同时存在,通过优化设计,球面成像系统可以近似达到或者接近理想成像系统,但不会完全达到理想成像系统.
3 结束语
通过本文的仿真实验,不但可以使学生更好地理解了工程光学中理想光学系统的概念和性质,还使学生学会了使用Matlab语言编程,增强了学生学习兴趣,拓展了学生的知识面,达到了事半功倍的效果. 本文的仿真实验还为像差理论的
学习打下了基础,也使学生提前接触到光学设计的内容,使学生对于工程光学这门课有了更全面深刻的理解.
[1] Hou J, Li H, Wu R, et al. Method to design two aspheric surfaces for imaging system [J]. Appl. Opt.,2013,52(11):2294-9.
[2] Miks A, Novak J, Novak P. Third-order design of aspheric spectacle lenses [J]. Optik-International Journal for Light and Electron Optics,2010,121(23):2097-2104.
[3] 韩雪冰,刘华,张文静,等. 二元光学元件在微光夜视物镜中的应用研究[J]. 长春理工大学学报, 2013,36(1/2):20-23.
[4] 郁道银,谈恒英. 工程光学[M]. 3版. 北京:机械工业出版社,2011.
[5] 何钰,吴平,张晓,等. Matlab在物理学中的应用[J]. 大学物理,2013,32(12):39-42.
[6] Qin H. Aberration correction of a single aspheric lens with particle swarm algorithm [J]. Optics Communications, 2012,285(13/14):2996-3000.
[7] Qin H. Particle swarm optimization applied to automatic lens design [J]. Optics Communications, 2011,284(12):2763-2766.
ApplicationofMatlabinsimulatedgeometricalopticsexperiments
QIN Hua, FENG Dong-tai
(School of Sciences, Shandong University of Technology, Zibo 255049, China)
When teaching of engineering optics, in order to enable students to better understand the difference between a spherical optical imaging system and an ideal optical imaging system, a simulation experiment using Matlab was presented. Structural parametersr,d,nandL(object distance) of an optical system were substituted into emulation programs, the imaging process of a spherical optical system could be emulated. The simulation results showed that the imaging properties of ideal optical imaging system did not exist in spherical optical imaging systems, however, spherical systems could approximately approach or infinitely close to the ideal imaging system by optimizing the design of the structure. The worth of an ideal imaging system lied in its standards.
geometrical optics; ideal imaging system; spherical optical imaging system; computer simulation
O4-39
A
1005-4642(2017)11-0013-05

2017-01-23
山东省自然科学基金资助(No.ZR2012FM001)
秦 华(1964-),男,山东临沂人,山东理工大学理学院副教授,博士,主要从事光学设计、全固态激光器及透明导电薄膜方面的研究工作.
冯东太(1961-),男,山东淄博人,山东理工大学理学院教授,博士,主要从事量子光学与量子信息方向的工作.
[责任编辑:尹冬梅]
