基于DSP和改进i p-i q算法的不对称系统补偿指令电流检测*
2017-12-20公茂法张旭童公政姜文
公茂法,张旭童,公政,姜文
(1.山东科技大学 电气与自动化工程学院,山东青岛266590;2.国网山东电力公司潍坊供电公司,山东潍坊261021)
0 引 言
近年来,在我国经济发展的带动下,大量的非线性负荷日益增多,如交流电弧炉、电力机车等,对工业生产运输具有重要的作用。这些负荷带来的非线性、冲击性影响使电网常常处于非理想状态下,表现为电压波动、三相不对称和谐波污染等。在补偿点加装静止无功补偿器(SVC)、有源电力滤波器(APF)等补偿装置是有效治理以上情形的必要手段之一。补偿的进行必须具有适应非理性状态的普遍性,因此,准确获取所用于补偿的指令信号电流尤为重要[1-3]。
传统的ip-iq算法基于瞬时无功功率理论,是实时检测谐波和无功电流的基础理论。其进行反变换得到基波分量前,通过断开ip或iq通道的方法来获取谐波和无功电流之和。这种算法的实现基础,是准确获取A相电压的相位信息,并转化为同频率的正、余弦值参与运算。但在电网非理想波形状态下,经由锁相环提取的并不是准确的相位信息[4]。本文针对以上误差的存在,增加提取三相电压参与α-β坐标变换,并给出其中最为关键的瞬时基波电流矢量的坐标求取方法,设计了相应的DSP软硬件检测实现方案,在不对称电压作用下的仿真环境中,利用MATLAB软件验证了检测、提取综合补偿指令电流信号的准确性。
1 i p-i q算法的理论基础及误差分析
ip-iq算法的运算思路是将静止的abc坐标系变换为旋转的α-β坐标系,进行一系列的运算、滤波后,再由反变换回到abc坐标系,得到需要的基波信息。具体步骤为,三相瞬时电流 ia、ib、ic与 abc/α-β坐标变换矩阵 C32相乘,得到 α-β坐标系中两相电流分量 iα、iβ。并行地由锁相环电路(PLL)同步跟踪A相电压ua,获取相位信息,并与正、余弦信号发生电路配合,产生与A相电压同相位、同频率的正余弦信号,组成变换矩阵C,与 iα、iβ相乘,得到 ip、iq。再经低通滤波(LPF),得到直流分量此时α-β坐标系中的交流分量被滤除,滤波后分离的直流分量经反变换后对应基波正序电流分量[5],同基波负序电流分量一起,可以作为计算SVC补偿导纳值的指令电流。而将系统负载电流与基波有功分量相减,即可得出系统谐波分量,这一电流量可作为APF的补偿指令电流。ip-iq运算方式的原理图如图 1所示[6]。
图1的原理图中,iaf、ibf和 icf为基波正序电流,iah、ibh和 ich包含谐波和负序分量;图中参与 abc/α-β变换或反变换的矩阵表示如下:

图1 i p-i q运算方式原理图Fig.1 Principle diagram of i p-i q calculating method
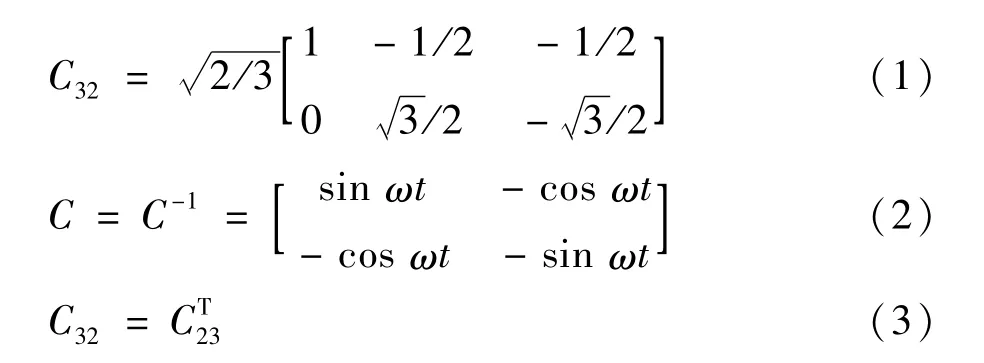
下面以三相三线制电网为例,通过引入相位误差θ,对ip-iq算法进行误差分析。零序电流不存在于三相三线制系统中,而零序电压分量可以在相电压中存在,所以将电流和电压分别表示为:
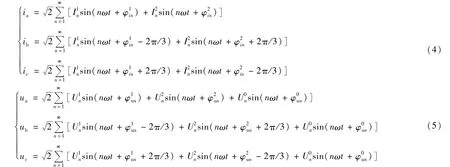
式中 下标n表示谐波次数,上标1、2、0分别对应正序、负序、零序,φ代表各序初相角。当电网由于负荷变动等因素进入不对称状态时,锁相环锁定A相电压的相位,而此相位并不等于A相正序电压的相位。设二者之间的相位偏差为θ,则引入θ后的正余弦转换矩阵为:
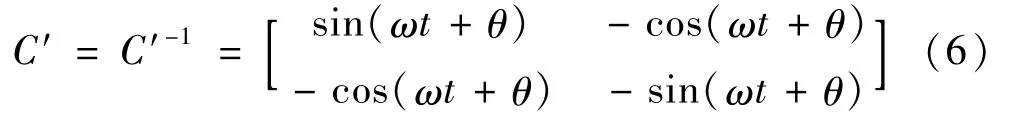
经低通滤波滤除交流分量,获取的直流分量为:
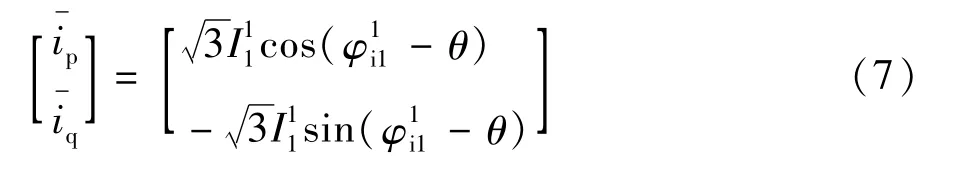
假设继续沿用切断ip或iq通道的方法,计算基波正序无功或有功电流,结果为:
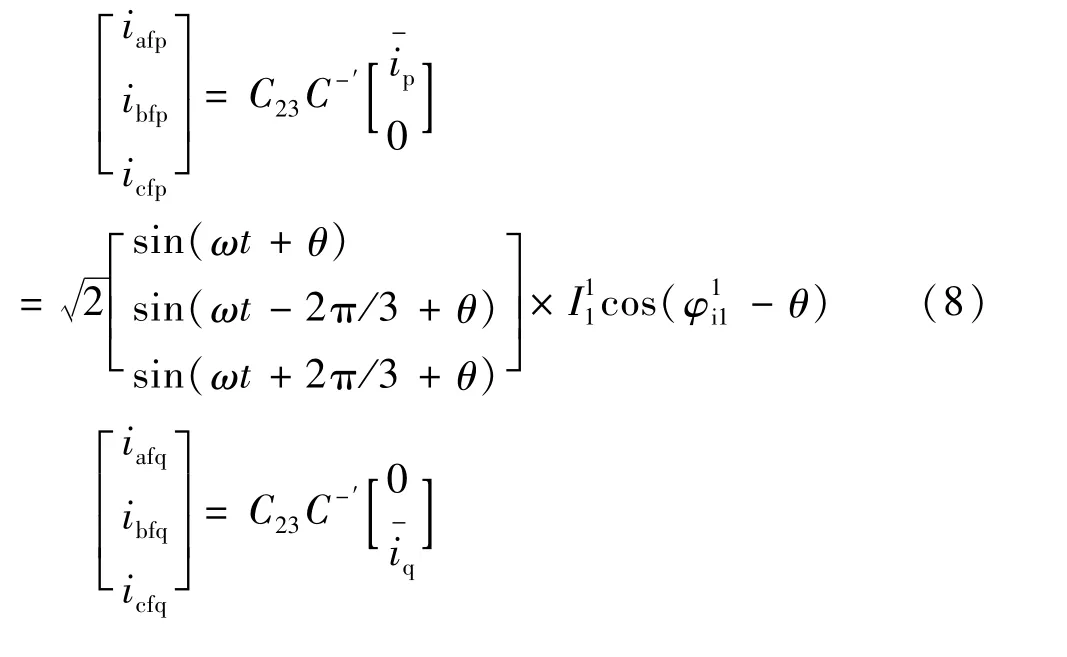
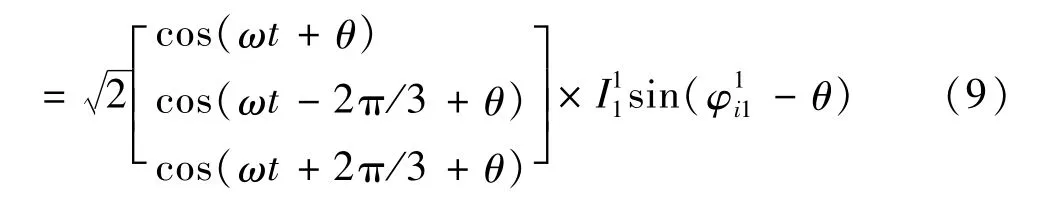
从式(8)、式(9)可以看出,无论是导出的无功电流分量还是有功电流分量,相位误差θ的引入最终反应到了基波正序有功、无功分量的运算结果中,使得进一步计算补偿信号产生偏差[7]。这是由于在不对称条件下,锁相环获取的相位ωt+θ,并不是基波正序电压的实际相位,而是各序分量和各次谐波作用后,综合产生的结果。
2 改进的i p-i q运算方式
如果能将正序电压分量也引入到变换计算中,锁相环所提取的相位误差问题将会迎刃而解。为了得到正序电压,必须将三相电压依照电流变换,参与到α-β坐标变换。图2所示为电压不对称时α-β坐标系中各矢量关系。
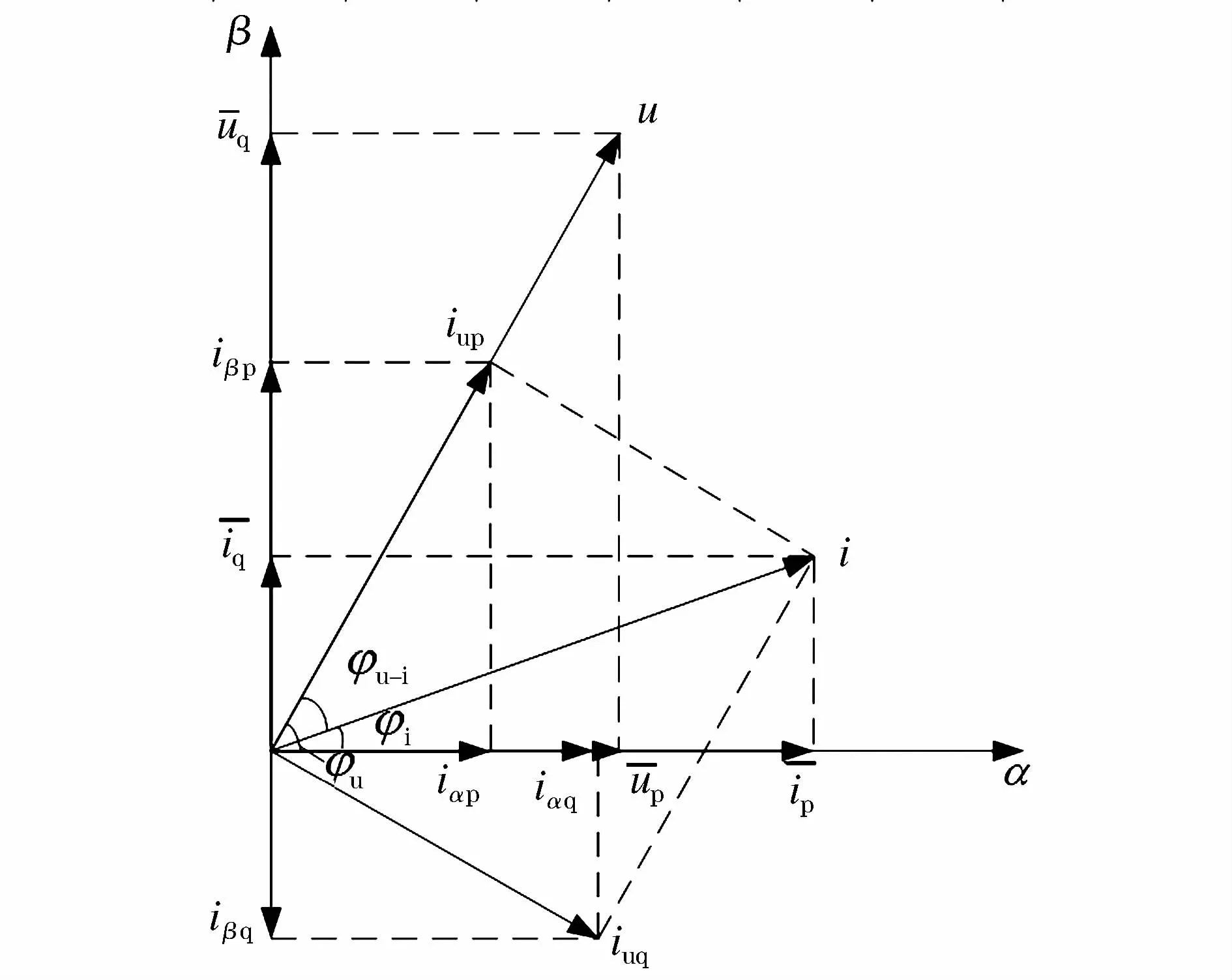
图2 电压不对称时α-β坐标系中各矢量关系Fig.2 Vector relationship inα-βcoordinate system under the condition of asymmetric voltage
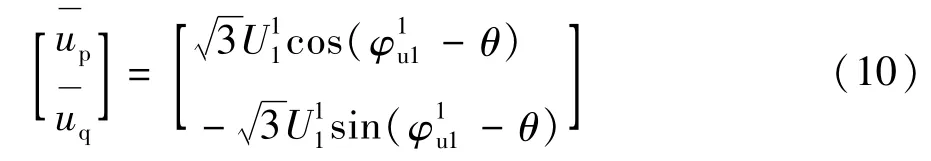
定义有功电流坐标系数M为:

定义无功电流坐标系数N为:

加入坐标系数M、N后,可以得出基波正序电压顺向有功电流矢量iup和电压垂直向无功电流矢量iuq,坐标分别为(iαp,iβp)和(iαq,iβq),计算方法为:
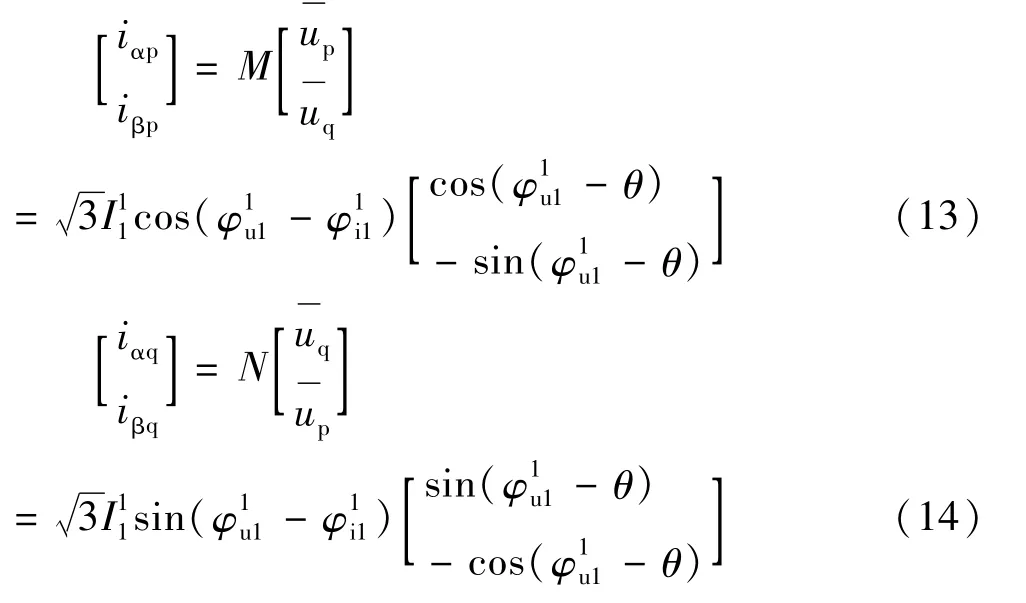
所得计算结果正是图2中基波正序电压顺向有功电流矢量iup和电压垂直向无功电流矢量iuq经分解后的坐标计算值,由此可以通过M/N运算求得坐标值,进而求得有功和无功分量。在上述运算过程中,虽然通过PLL检测到的同步信号相位仍是ωt+θ,但因为参与运算的都为瞬时正序参量,即使在发生三相电网电压不对称情况下仍能满足检测的需求,避免相位误差引起的干扰,确保运算准确性[8]。此时得到的瞬时正序电流对应变换前的基波电流。
在获得瞬时正序有功、无功电流矢量后,参照改进前的步骤,可进行α-β/abc反变换,即分别与反变换矩阵C23C-1相乘,得到相应的三相基波正序电流的有功分量 i′afp、i′bfp、i′cfp和无功分量 i′afq、i′bfq、i′cfq。若将负载电流 ia、ib、ic与 i′afp、i′bfp、i′cfp相减,即可得出ia、ib、ic的谐波分量和无功分量之和 iad、ibd、icd,作为APF和SVC等补偿系统的指令电流。图3所示为改进后的ip-iq运算方式原理图。

图3 改进的i p-i q运算方式原理图Fig.3 Principle diagram of improved i p-i q calculating method
3 检测系统的DSP实现
3.1 系统硬件设计
图4示出检测系统的硬件设计结构框图。数字信号处理器(DSP)选用TMS320F2812芯片,其本身带有12位A/D转换器,可实现最多16路模拟信号的输入,最高转换速率可达80 ns/12.5 Msps,完全满足数据采样的需求。
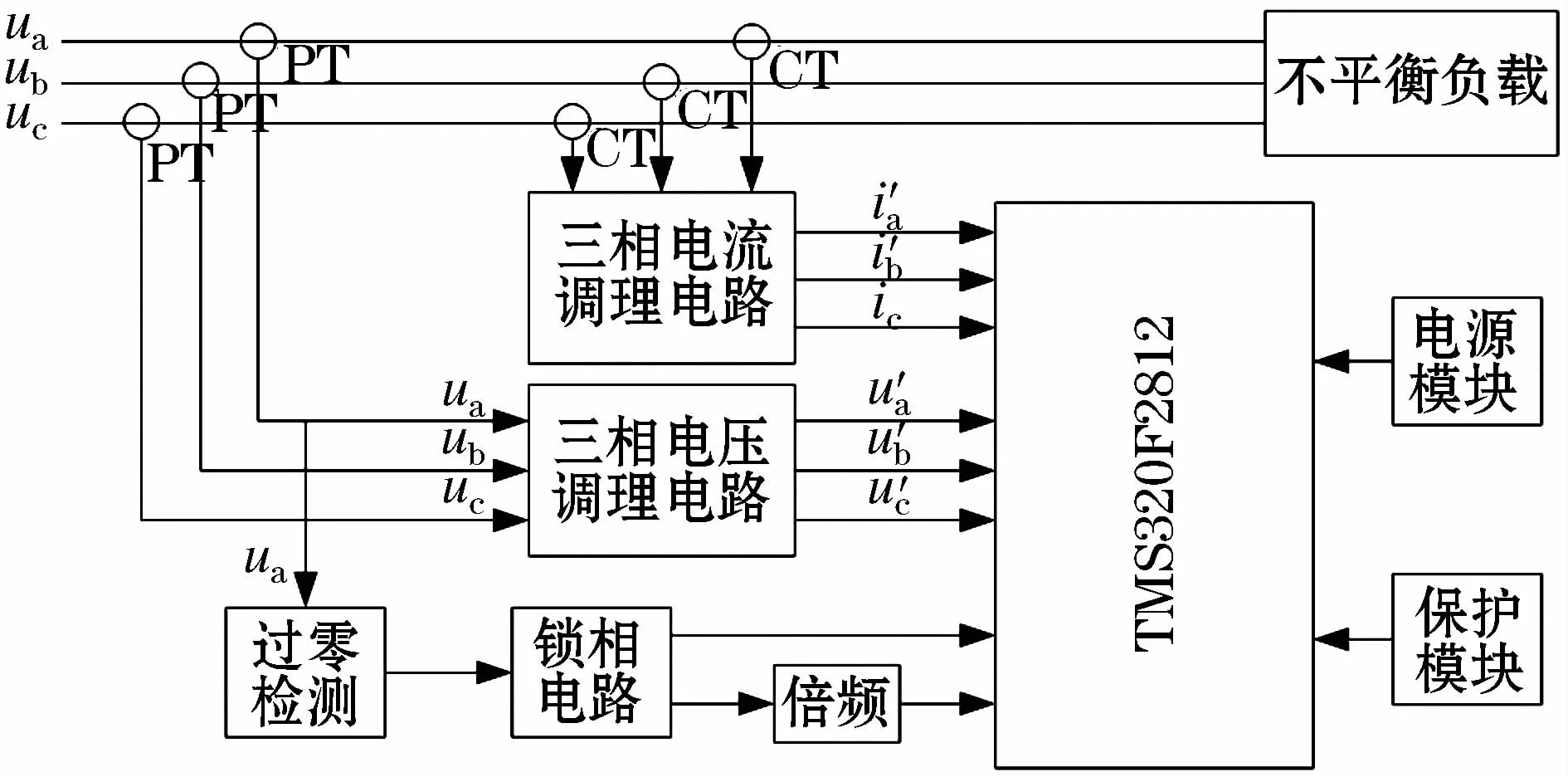
图4 检测系统的硬件设计结构框图Fig.4 Hardware design structure block diagram of the detection system
三相电网电压和电流首先经过电压互感器(PT)和电流互感器(CT)转变成弱电信号,经信号调理电路转换成单极性信号(如电压为0 V~3.3 V),这是DSP片上A/D转换器采样信号输入的合理范围。经过调理后三相电压、三相电流信号分别接入DSP的ADC INA 1~3和ADC INB 1~3,六通道采用双排序模式进行同步采样,通过选择保持后送入模数转换器,并把转换的数据结果存入对应的缓冲寄存器(ADCRESULTn)中。由于检测算法经过改进,不需要考虑不对称和谐波干扰情况下的相位误差,所以仍然采用锁相电路来获取同步信号,作为调用正、余弦函数表和启动 A/D转换的基准。锁相电路选用COMS锁相环集成芯片CD4046来实现。A相电压通过过零检测电路和锁相电路后分为两路:一路直接接入DSP的CAP_3捕获引脚,在A相电压每次从负到正过零时,实现正、余弦表的准确复位;另一路经128倍频(6.4 kHz)后接入到处理器的 CAP_6引脚,控制采样保持器并作为A/D转换的启动信号。考虑到电网工频频率在负荷变化等因素影响下的波动性,信号的频率往往不能严格等于50 Hz,采用128倍工频作为A/D转换同步采样频率,即每个工频周期内均匀采样128点,使采样的不确定性减小,从而消除电网频率变动造成的采样误差[9-11]。
3.2 系统软件设计
在检测算法中,由PLL锁相得到的相位信息要转换成正、余弦值参与变换,并且参与运算的量都是经低通滤波后的直流量,所以在软件设计部分,参考正余弦的产生和滤波程序是整个程序编制的关键,以上均由中断服务程序实现。正、余弦函数表可以用MATLAB命令生成,与CAP_3引脚捕获的过零跳变信号配合准确复位,利用查表的方法实现。数字低通滤波选用128阶的有限脉冲响应滤波器(FIR),其实质为一周期内采样128个相邻输入的平均值滤波器,滤波器传递函数为:
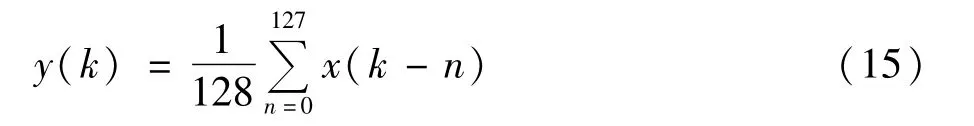
图5所示为中断服务主程序的执行流程图。
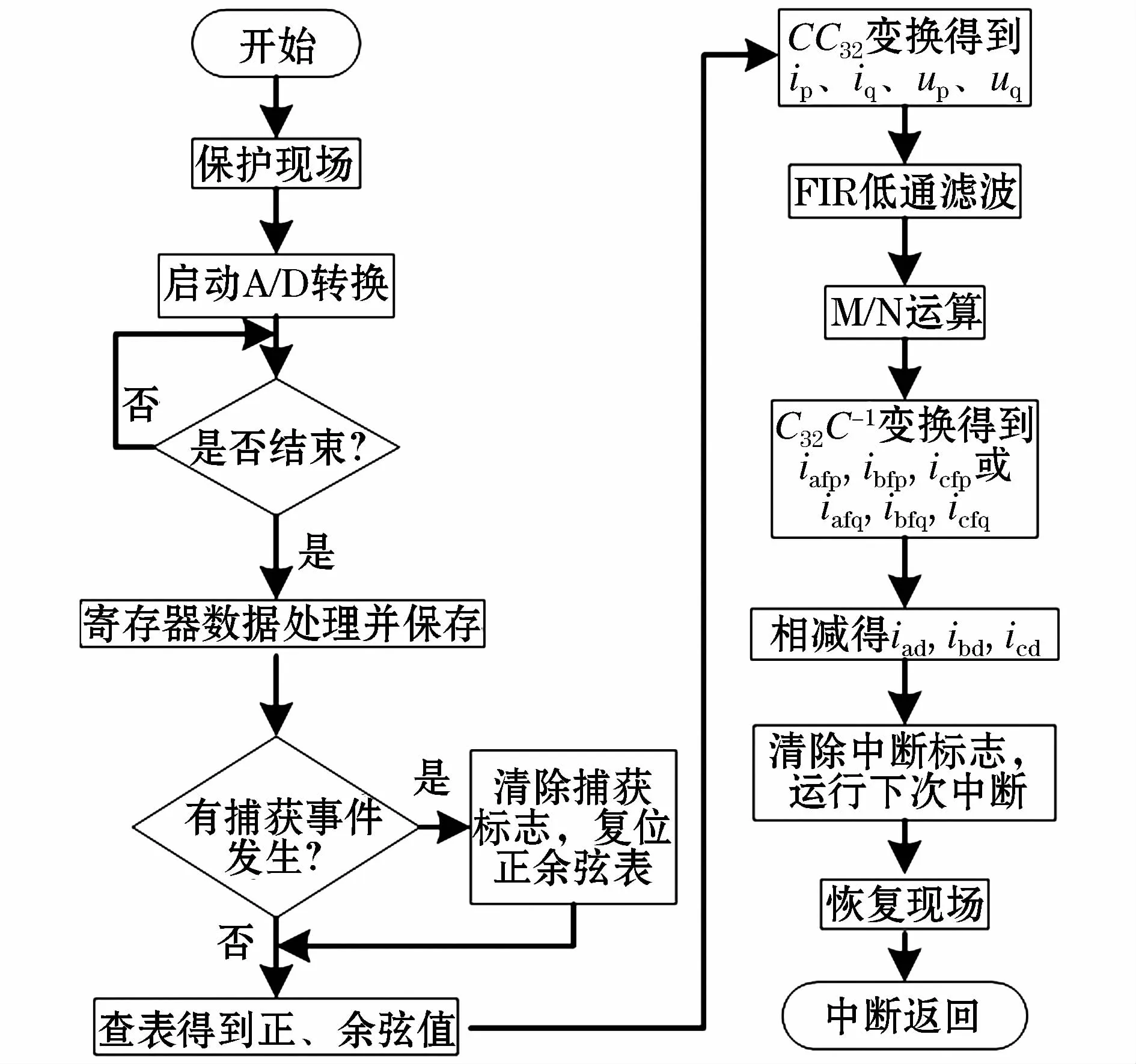
图5 中断服务程序流程图Fig.5 Flow chart of interrupt service routine
4 不对称系统MATLAB仿真
如果能够证明三相基波正序有功电流 i′afp、i′bfp、i′cfp检测准确,那么与之并行的无功电流 i′afq、i′bfq、i′cfq和其参与运算得出的补偿信号iad、ibd、icd也会是准确的,即证明改进ip-iq检测算法在不对称系统中相较于传统ip-iq算法更适应、更精确。所以在本文的仿真算例中,对比改进前后检测到的三相基波正序有功电流波形,进行定量分析,判断改进后方法是否更精确。
仿真在MATLAB/SIMULINK环境搭建不对称系统进行。为方便叙述,仅以A相为例进行比较说明。系统选用三相整流桥电路作为非线性负载,负载电阻10Ω,电感1 mH,三相不对称电压各相有效值为220 V,A、B和 C三相的初相位分别为25°,-130°,120°。图6示出三相负载电流的波形,可见负载电流呈不对称且含有大量谐波和无功分量。
通过未改进前断开iq通道的方法获取到的A相基波正序有功电流波形如图7所示。
通过加入M/N算式改进后的ip-iq运算方式检测到的A相基波正序有功电流波形如图8所示。
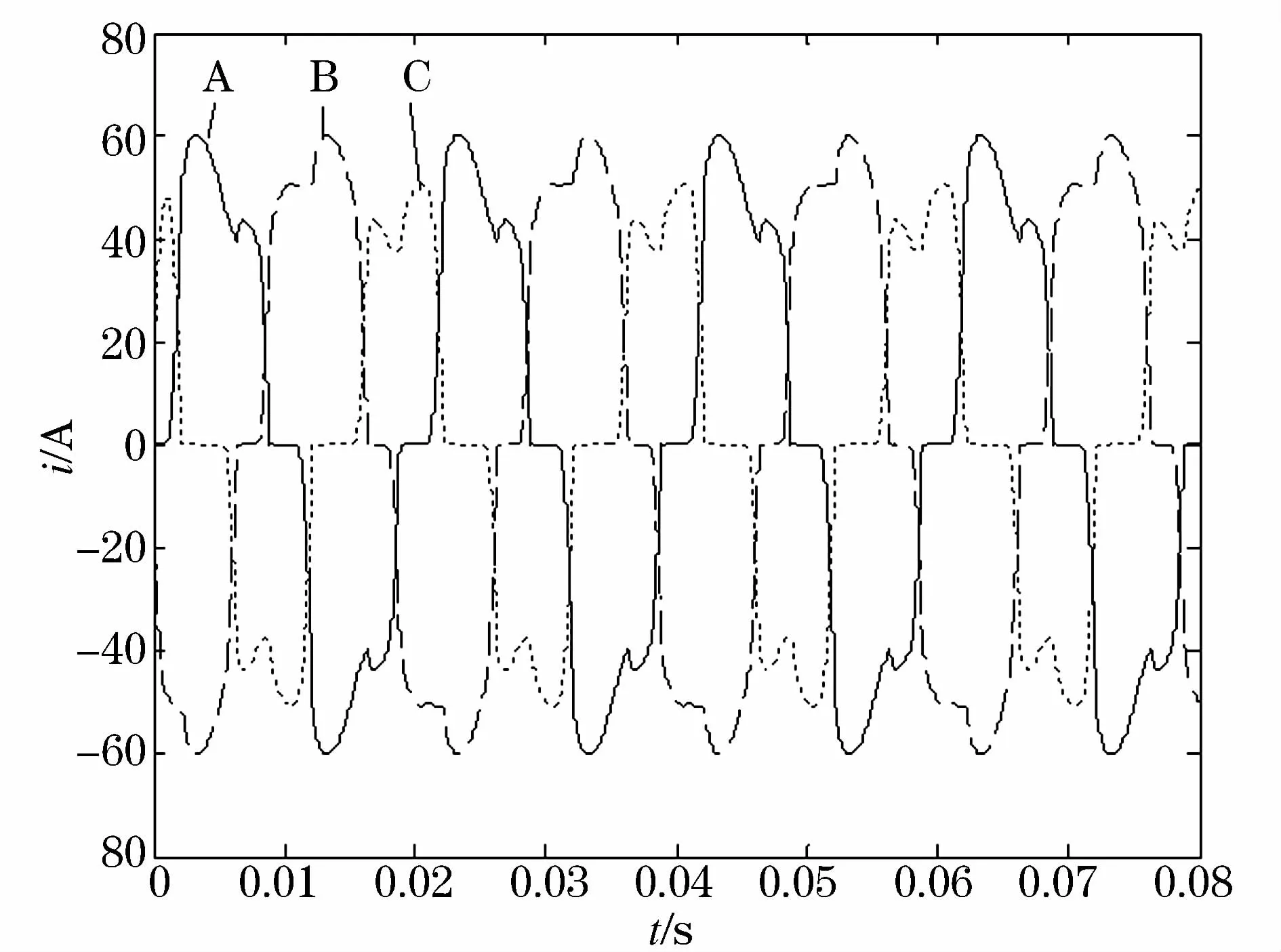
图6 电网电压不对称系统三相负载电流Fig.6 Three-phase load current of power grid voltage in asymmetric systems

图7 改进前A相基波正序有功电流Fig.7 A-phase fundamental positive active current obtained by unimproved method
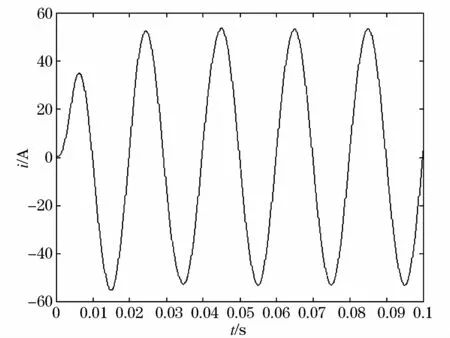
图8 改进后A相基波正序有功电流Fig.8 A-phase fundamental positive active current obtained by improved method
从直观观察,改进后的波形响应速度更快,形状更加完善且稳定。通过SIMULINK电力系统模块库中的快速傅里叶变换(FFT Analysis)模块,以50 Hz为基频频率进行频谱分析,对比改进前后波形的质量,所得的对比数据如表1所示。

表1 对比结果Tab.1 Comparison results
分析改进前后对比数据可知,改进后的总谐波失真(THD)比例更低,更接近于标准的正弦基波形式,从而证明了改进后的系统在不对称条件下,对于补偿信号的检测更为精确和稳定。需要说明的是,本文在仿真时设定的初相角仅为发生不对称时的一种情况,且条件较为苛刻,仿真中经多种不对称度测试均能准确检测出补偿分量,证明改进的ip-iq运算方式对一般形式的不对称系统仍然适应。
5 结束语
通过增加三相电压参与坐标变换的方法,改进ip-iq运算方式,并通过引入M/N算式,利用数值计算方法,求取α-β坐标系中瞬时基波正序有功和无功电流矢量坐标,使不对称电网系统综合补偿指令信号的获取较传统方法更为准确,设计了基于DSP实现的检测系统,并在MATLAB仿真环境下验证了发生不对称情况时改进方法的精确性,具有一定的实用价值。
