基于谐波畸变功率的谐波源定位研究*

白志轩，肖先勇，张逸，汪颖，陈飞宇

（1.四川大学电气信息学院，成都610065；2.国网福建省电力有限公司电力科学研究院，福州350000）

0 引 言

随着社会经济和智能电网的快速发展，大量电力电子设备等非线性负荷接入电网［1］，公共连接点（Point of Common Coupling，PCC）处电压和电流畸变越来越严重，由此造成了严重的谐波污染和经济损失。PCC点处主谐波源的正确定位是电力系统治理谐波污染，明确谐波源的发射水平和污染责任的前提，是谐波分析与治理领域中的首要问题，具有重要的意义［2］。

IEEE 519标准［3］中定义了总谐波畸变率（THD）指标，这是目前应用最广泛的谐波指标之一，虽然限制THD值可以管理每个负荷的谐波污染，但是它只能确定高次谐波分量对波形畸变的程度，在分析电力系统中的污染负荷影响时仅仅用THD指标是不够的［4］，而且目前的国际标准中并没有定义或者建议任何定位主谐波源的测量方法和指标。因此国内外学者对谐波源定位方法和指标展开较多的研究，并取得了诸多成果［5-7］。根据现有的测量方法可以将谐波源定位方法分为两类：单点测量法和分布式测量方法［7］。分布式测量法基于分布式测量系统和电网中不同点同步收集数据，通过谐波状态估计计算出系统中各支路的谐波电流及各母线的谐波电压进行谐波源位置的判定，该类方法可以提供电网中谐波传播的精确和完整信息，但由于将多个节点电压作为状态变量增加了运算方程组的复杂程度而且成本昂贵在实际中难以广泛应用［8］。单点法可以将PCC点主谐波源定位于测量点的上游（电网侧）或下游（用户侧）［9-10］。虽然单点法精确度不如前者，但其操作简单更易于工程应用。最常用的单点法是谐波有功功率方向法，但是其由于受到功率角的影响准确率不高，容易失效［11］。文献［12］从无功功率的角度出发提出了一种主谐波源定位方法：通过比较Sharon无功功率Qsh与基波无功功率Q1、非有功功率N的大小，判断主谐波源位置。此后，有学者进一步定义了虚功率（Fictitious Reactive Powr）Qx，并以此代替Qsh［13］，但当额定功率较小时，其准确率不高，且对测量仪器的精度有很高的要求。文献［14］提出了一种基于Budeanu（布氏）畸变功率的主谐波源定位方法，但布氏功率分解方法存在弊端且物理意义不够明确［15］。在 2010年修订的 IEEE Std.1459-2010［16］标准中，Emanuel（尹氏）功率理论代替了原有的布氏无功功率QB和畸变功率DB，其基本思想是把基波产生的有功和无功与剩余的视在功率分离开来，具有更合理的物理意义［15］。而且在 IEEE Std.1459-2010［16］功率定义标准实施以来，将其应用于谐波源定位的研究还很不足。目前很多学者针对该标准研制相关的功率计量装置［17］，提出的方法符合该标准的要求，易于推广应用于最新的功率计量装置中，从而在工程上实现应用。

文章从功率的角度出发，提出了一种基于谐波畸变功率的谐波源定位单点测量法，实现了适用于IEEE Std.1459-2010标准［16］的PCC点主谐波源定位。首先在第一节中介绍了IEEE.1459-2010中的谐波畸变功率分量的定义，并从瞬时功率分解的角度对该分量进行了分析。第二节中通过比较线性负荷和非线性负荷在同一供电条件下谐波畸变功率的差异，证明了谐波畸变功率可以作为指标定位PCC点主谐波源，进而提出了本文的方法，并推广到三相系统中。第三节中对IEEE测试系统［18］进行仿真分析所提方法，并且通过第四节实验验证进一步证明了该方法的正确性和有效性。

1 谐波畸变功率分量的定义

非正弦周期性电压和电流瞬时值在稳态条件下可以分成如下两部分：

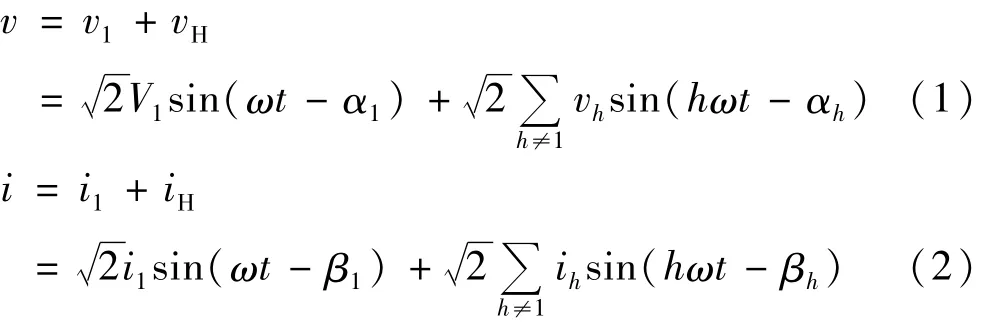
式中v1和i1分别是基波电压和电流；vH和iH分别包含所有剩余谐波电压、电流分量；V1和I1分别代表基波电压和电流的有效值；Vh和Ih分别是第h次谐波的电压电流有效值；α1和β1分别是基波电压和电流的相位；αh和βh是第h次谐波分量的相位；ω为基波角频率。

基波、谐波电压和电流有效值之间的关系为：

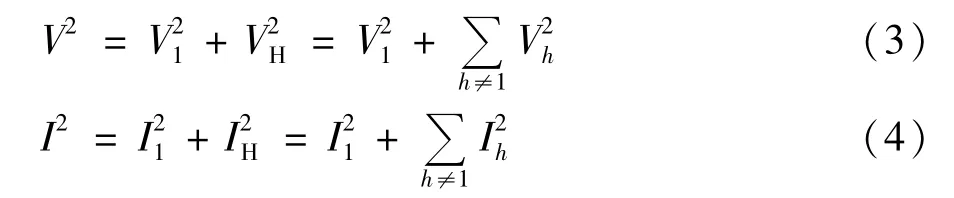
式中VH、IH分别为vH和iH的有效值。

将视在功率S分解如下：

式中S1为基波视在功率；DI，DV分别为电流、电压畸变功率；SH为谐波视在功率［15］。

谐波电流有效值的平方Ih2可分解为两个正交分量：

式中 θh＝βh－αh，为h次谐波电压与谐波电流的相位差。

根据式（6）和拉格朗日恒等式［15］，SH可分解为：

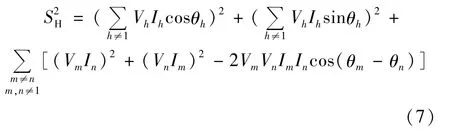
式中Vm、Im分别为m次谐波电压电流的有效值；Vn、In分别为n次谐波电压电流的有效值，θm、θn分别为m次、n次谐波电压与谐波电流的相位差。

定义谐波畸变功率如下［15］：

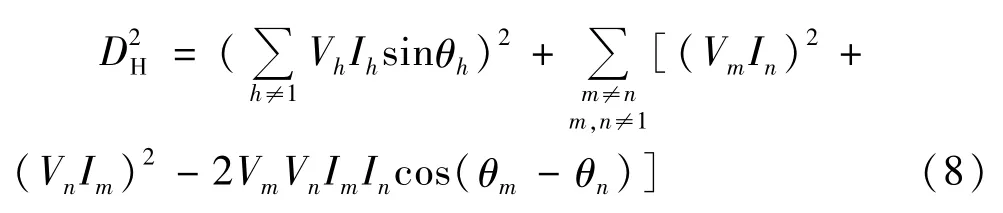
IEEE Std.1459-2010标准采用了式（8）定义的谐波畸变功率DH。谐波畸变功率DH不包含基波电压和基波电流分量，文献［15］分别将基波电压和基波电流与谐波电压和谐波电流的相互作用定义为电流畸变功率DI和电压畸变功率DV［15］，分别来度量电流畸变和电压畸变对视在功率的贡献程度；而谐波畸变功率DH是各非基波次谐波电压、谐波电流相互作用的结果。

下面从瞬时功率的角度分析上述功率分解方法，将瞬时功率分解如下：

式中pa、pq分别为瞬时功率的有功、非有功分量。

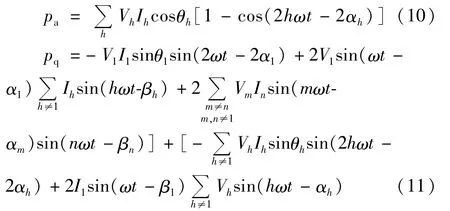
式中pa为有功功率的瞬时分量，其平均值为总有功功率；pq包括所有平均值为零的分量。可分为四个分量。式中第一项对应基波无功功率以两倍基频振荡，其振荡幅值就是基波无功功率的值，第二项和第三项分别对应式（5）中的电流畸变功率DI和电压畸变功率DV；最后一项为不同频次谐波电压电流之间的乘积，该信号分量的幅值大小与式（8）谐波畸变功率DH的大小具有对应关系。

2 基于谐波畸变功率的谐波源定位方法研究

2.1 线性负荷接入含背景谐波电压的供电网

当电网侧含有背景谐波电压，用户侧接入线性负荷时，此时用户侧也会有谐波电压和谐波电流，戴维南等效电路如图1。

图1 含背景谐波电压的电网给线性负荷供电Fig.1 Linear load supply with background of harmonic voltage

图中 Rc、Ru和Lc、Lu分别为电网侧和用户侧等效参数，vu、vc分别为电网侧和用户侧电压。

电网侧电压为：

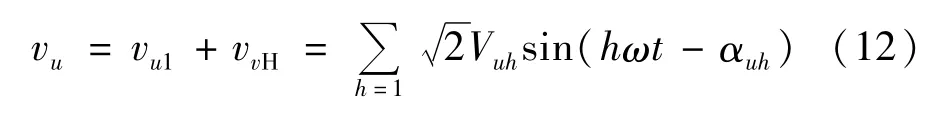
式中 vu1、vuH分别为电网侧基波、谐波电压；Vuh、αuh分别为电网侧h次谐波电压的有效值和相位。

图1中，PCC点的电流为：

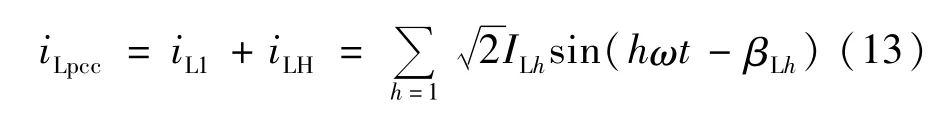
式中iL1、iLH分别为PCC点基波、谐波电流；ILh为h次谐波电流的有效值；βLh为h次谐波电流的相位。

在谐波情况下由基尔霍夫电压定律［15］得PCC点谐波电压为：

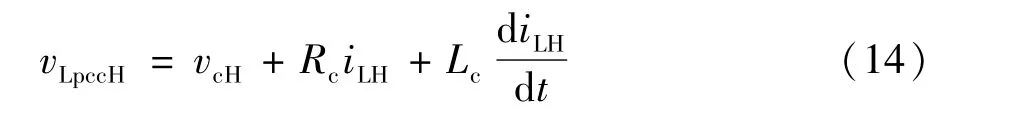
式中vcH为用户侧谐波电压。

PCC点谐波电流iLH引起的瞬时功率为：

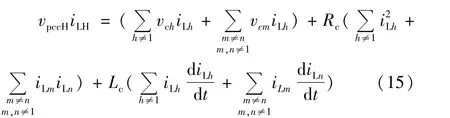
式中vcm为用户侧m次谐波电压；iLn、iLm分别为线性负荷情况下n次和m次谐波电流。

根据式（11）可知，式（15）中与PCC点谐波畸变功率DH对应的瞬时分量pDHL为：

2.2 非线性负荷接入含背景谐波的供电网

类似地，用户侧接入的负荷换为非线性负荷时，戴维南等效电路如图2，电网侧的电压同样如式（12），此时用户侧电压为 v′c，PCC点电压为 vNpcc。

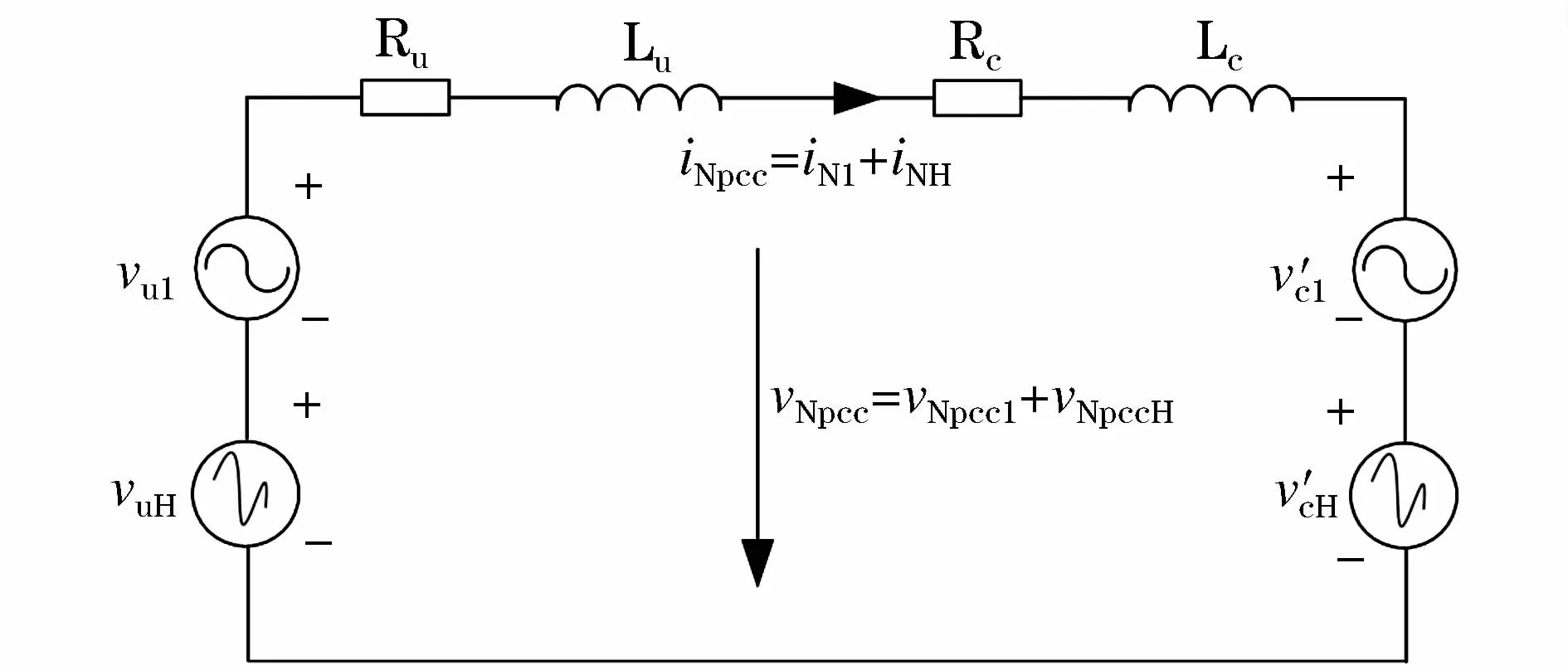
图2 背景谐波电压供电非线性负荷Fig.2 Nonlinear load supply with background of harmonic voltage

此时PCC点的电流为：

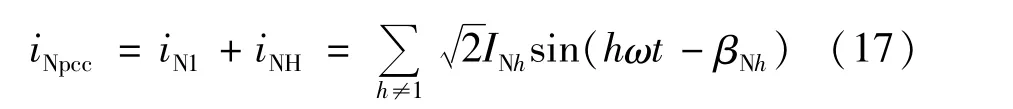
式中iN1、iNH分别为PCC点基波、谐波电流；INh和βNh分别为h次谐波的电流有效值和相位。

同理可得，与谐波畸变功率DH对应的瞬时分量pDHN为：

对比式（16）和式（18）发现，在电网参数相同时，两瞬时分量的幅值主要取决于谐波电压和谐波电流含量的大小。根据文献［2］流经线性负荷的谐波电流是本次谐波电压的线性函数，而流经非线性负荷的谐波电流是各次谐波电压的复杂函数。在同一视在功率数量级下，当电网侧含有背景谐波电压，用户侧接入的负荷为线性负荷时，PCC点谐波电流含量很低，因此，与瞬时分量pDHL幅值对应的DH值也很小；反之，如果用户侧接入的负荷为非线性负荷时，非线性负荷作为谐波源会注入谐波电流，所以谐波电流含量会比前者大的多，必然导致瞬时分量pDHNL幅值明显增大，与其对应的DH值也会相应增大。式（18）中由于非线性负荷NL的影响，电流iNh的幅值大于iLh，导致瞬时分量pDHN的幅值大于pDHL，所以与其相对应的DH值大小会有明显差别。

2.3 基于谐波畸变功率的谐波源定位方法

通过上述分析，本文提出基于谐波畸变功率的PCC点主谐波源定位方法：在PCC点测量计算谐波畸变功率DH，当该点DH有较大值时定位用户侧为主谐波源，否则为电网侧为主谐波源。

通过式（8）计算DH比较困难，根据IEEE Std.1459-2010标准［16］推导出DH计算式如下：

式中S1为基波视在功率；THDI和THDV分别为电流、电压总谐波畸变率；PH为谐波有功功率。

对于三相非正弦或／和不平衡系统，可根据等效视在功率（Equivalent Apparent Power）的方法将三相等效为单相将本文方法推广到三相系统［19］。

3 IEEE测试系统仿真分析

为了验证本文方法的有效性，作者基于PSCAD／EMTDC对IEEE 13节点配网系统［18］进行了计算机仿真。测试系统如图3所示，系统由节点50供电，由电压调节器，三相和单相负荷等组成，谐波源负荷成分包括日光灯组、变频调速系统（ASD）和家用负荷［18］。本文针对三种不同工作情况在该系统中选取五个测量点，如图3所示：节点32（包括用户侧的所有负荷），节点33（包括节点34的负荷），节点45（包括节点45和46的负荷），节点92（包括节点92和75的负荷），节点84（包括节点911和52的负荷）。

在三种不同的谐波源负荷方案下（注入谐波源不同）进行仿真验证，在每个测量点应用本文提出的方法，并与文献［13］提出的比较三种非有功功率法（基波无功功率Q1，虚拟无功功率Qx和非有功功率N，当Qx值更接近Q1时定位主谐波源在电网侧，否则主谐波源在用户侧）的结果进行对比，每种方案下测量点的采样值导入Matlab处理计算得到DH和Q1，Qx，N。

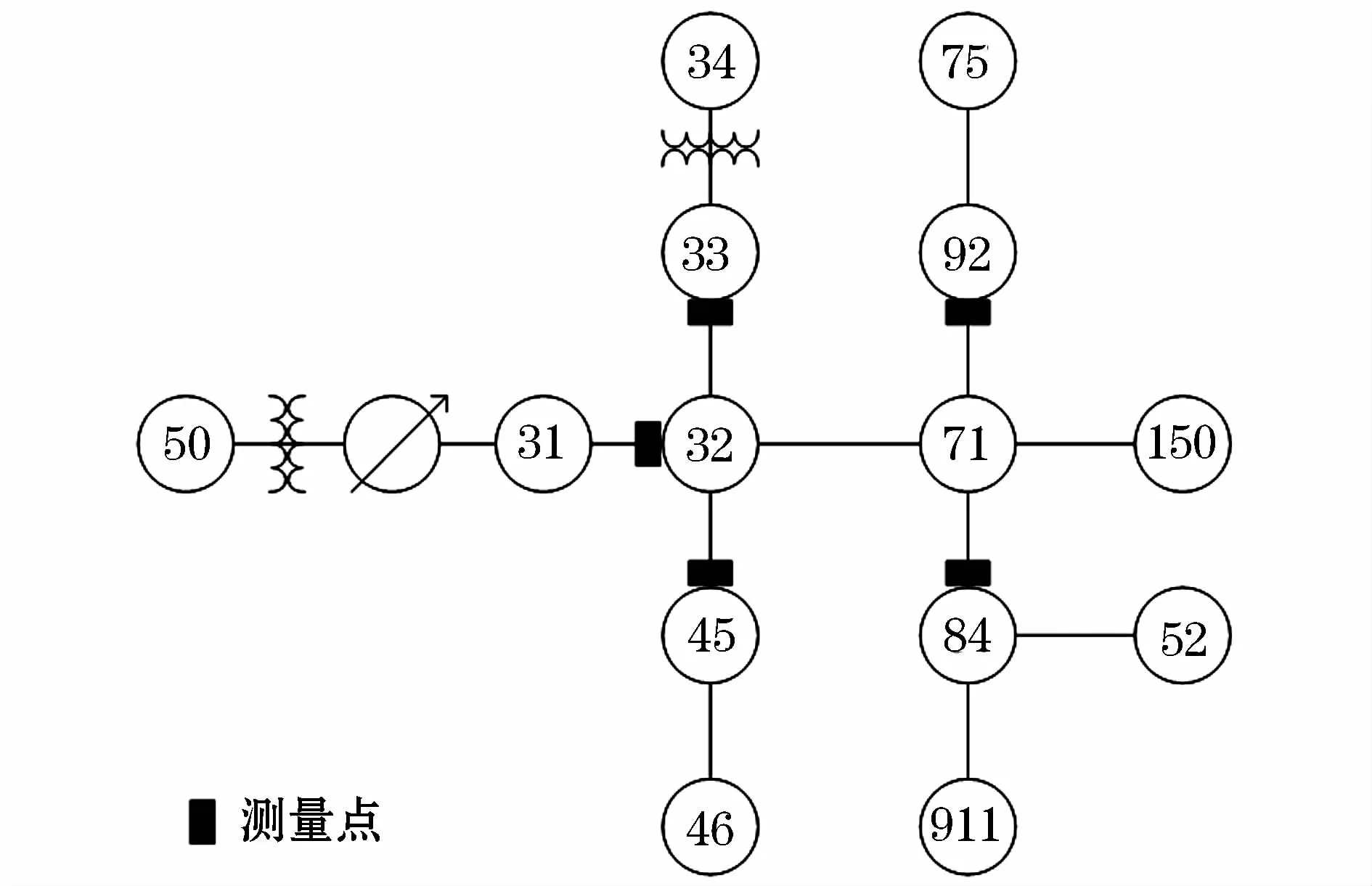
图3 IEEE测试系统Fig.3 IEEE test system

方案1：作者在节点75和92注入谐波源作为第一种情况，此时两种方法的结果分别如表1和图4所示。测量点32和92的实际结果是用户侧为主谐波源，其余测量点实际结果应为电网侧为主谐波源。由图4可见，测量点33，45和84谐波畸变功率非常小，这说明此处没有非线性负荷，主谐波源应该在电网侧；但是对于节点32和92的DH值比前者大的多，说明主谐波源存在于用户侧。因此本文提出的基于DH的方法在所有测量点都给出了正确的结果。由表1可见，因为在节点32和92 Qx更接近于N，所以基于对比三种非有功功率的方法同样在所有测量点给出了正确的结果。

方案2：第二种情况是作者在节点75，92，45和46注入谐波源，此时节点32，45和92的实际结果是用户侧为主谐波源，其余测量点是电网侧为主谐波源，仿真结果分别如表2和图5和所示。由于节点32，45和92的谐波畸变功率DH值较大，定位主谐波源为用户侧，其余节点为电网侧，本文提出的方法在各个节点均给出了正确结果；如表2所示，因为Qx更接近于Q1，文献［13］的方法在测量点45处给出了错误的结果。

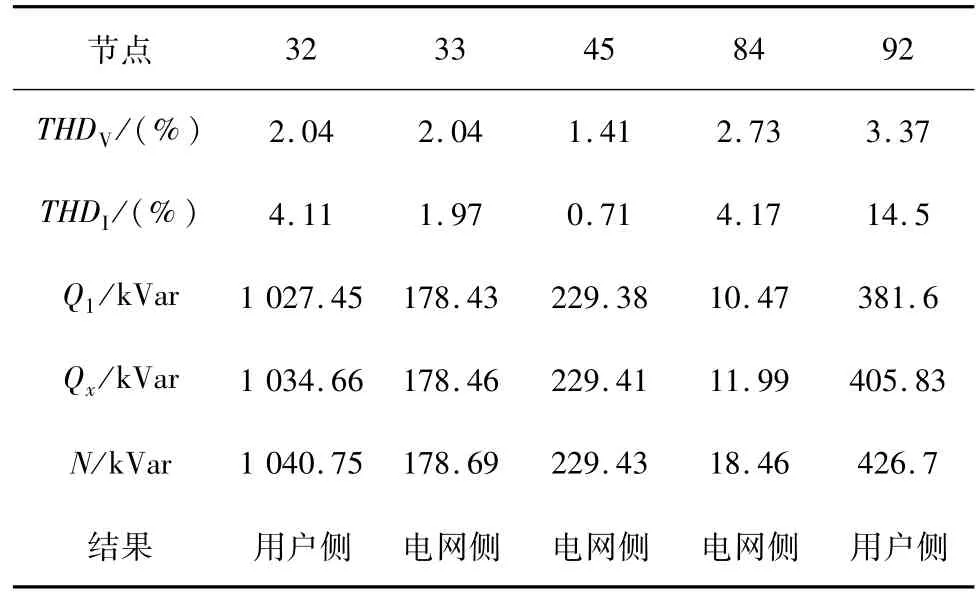
表1 方案1仿真结果（对比非有功功率法）Tab.1 Simulation results of case 1（the comparison of the reactive powers method）

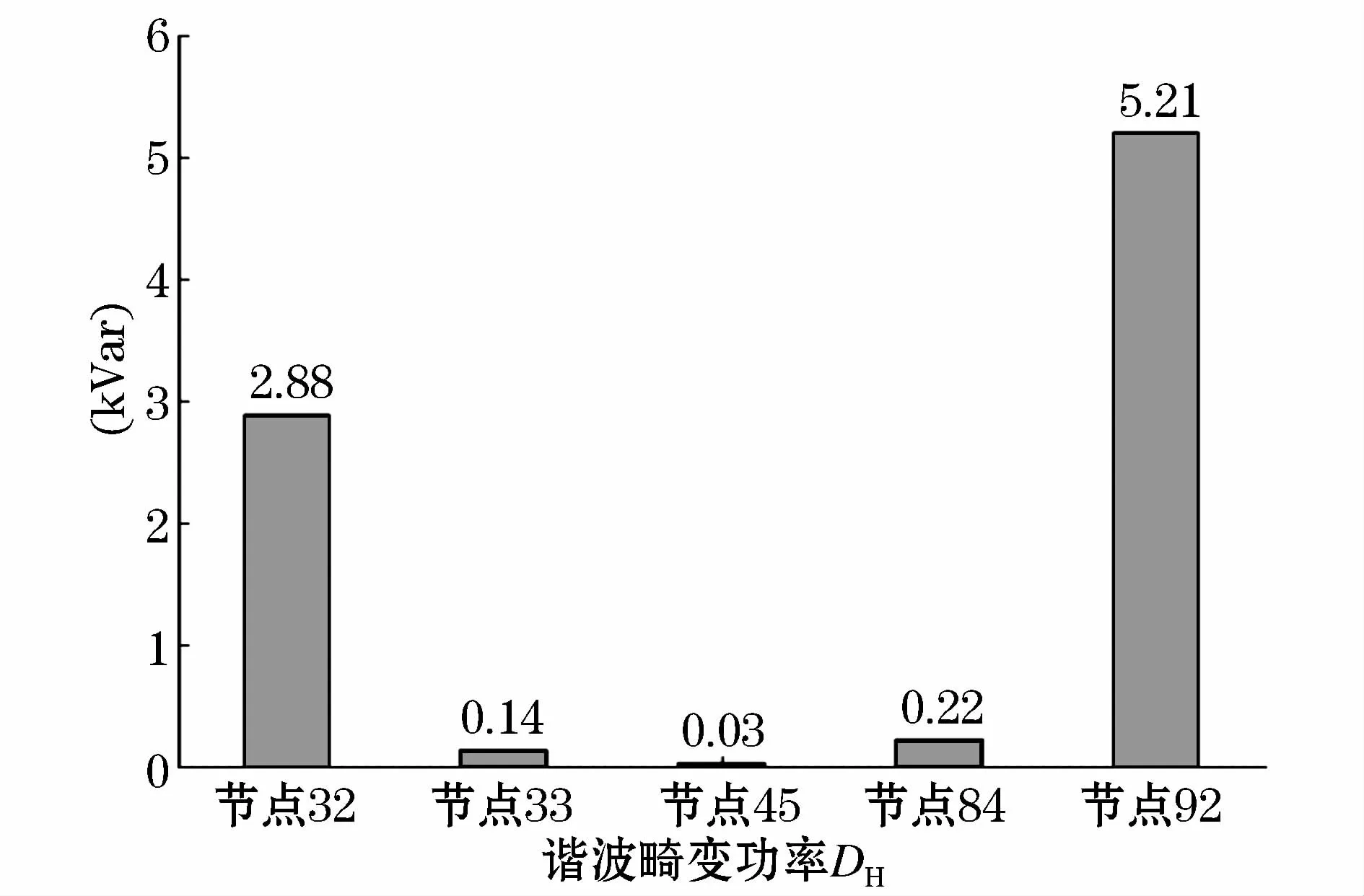
图4 方案1仿真结果（本文提出的方法）Fig.4 Simulation results of case 1（the proposed method）

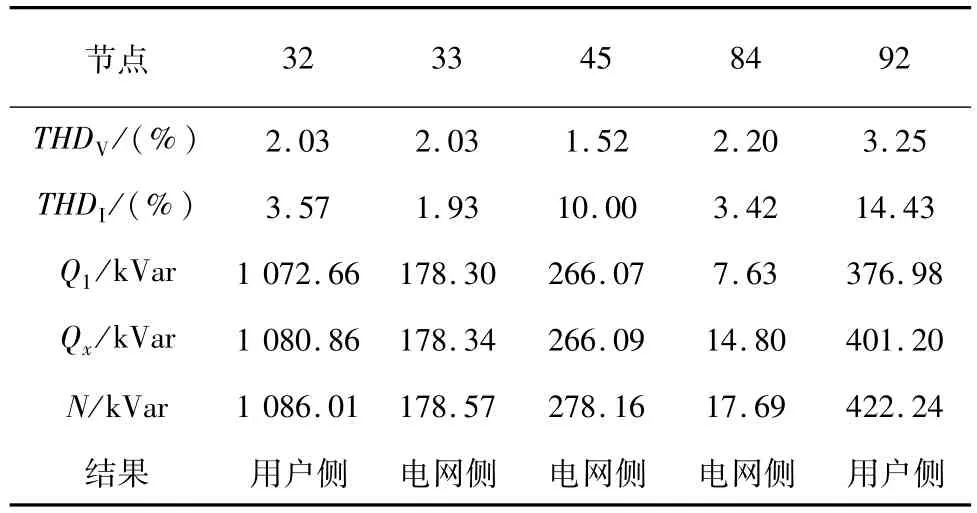
表2 方案2仿真结果（对比非有功功率法）Tab.2 Simulation results of case 2（the comparison of the reactive power method）

图5 方案2仿真结果（本文提出的方法）Fig.5 Simulation results of case 2（the proposed method）

方案3：第三种情况是作者在节点75，92，45，46，52和911注入谐波源，此时节点32，45，84和92实际结果是用户侧为主谐波源，仿真结果如表3和图6所示。谐波畸变功率DH在节点32，45，84和92都有较大的值，本文方法定位以上四处节点用户侧为主谐波源，而节点33由于DH值很小，故定位电网侧为主谐波源，本文提出的方法在各个节点均给出了正确结果；而文献［13］的方法在节点45给出了错误的结果。

表3 方案3仿真结果（对比非有功功率法）Tab.3 Simulation results of case 3（the comparison of the reactive powers method）

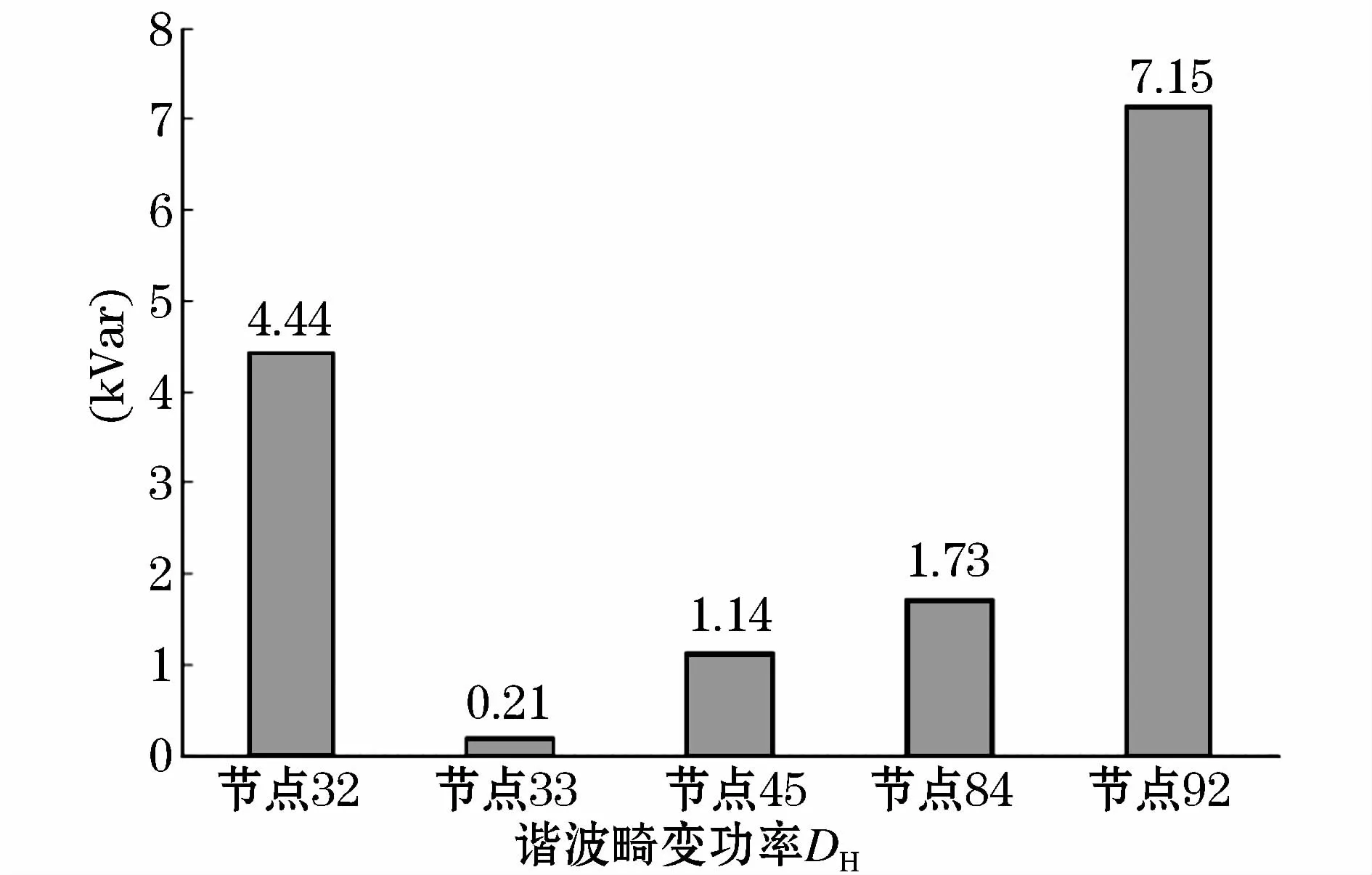
图6 方案3仿真结果（本文提出的方法）Fig.6 Simulation results of case 3（the proposed method）

4 实验结果与分析

在实验室环境下，将热水器、电脑、空调（制冷模式）、空调（制热模式）等典型家用电器接入同一PCC点，模拟接入供电网的不同负荷进行简单的原理性测量验证。实验采用高精度波形记录仪在各负荷侧同步记录电压和电流波形，仪器采样频率为10 kHz，如图7。基于Matlab对采样值每10个周波处理计算后得到谐波畸变功率DH变化结果如图8所示，测量结果的平均值如表4所示。

图7 测试仪器和波形记录Fig.7 Equipment of measurement and waveform record

由表4可见，在背景谐波在限值内的情况下（THDV为2.7%左右），由于实测的家用电器视在功率较低所以各负荷均有较低的谐波畸变功率。由于热水器主要由电阻丝构成，属于线性电阻负荷，虽然视在功率较大，但是其谐波畸变功率仅为0.68 Var，远小于其他负荷的值；而电脑中含有大量电力电子器件，是家用电器中典型的谐波源负荷，虽然其视在功率远小于热水器的1 394.16 VA，仅有98.97 VA的值，但其谐波畸变功率却达到1.69 Var，比前者的值大的多，同理两种工作状态下的空调都对电网产生了不同程度的谐波污染，其谐波畸变功率也比较大。由于谐波源的接入，PCC点处谐波畸变功率也有较大的值，各负荷谐波畸变功率变化如图8所示。

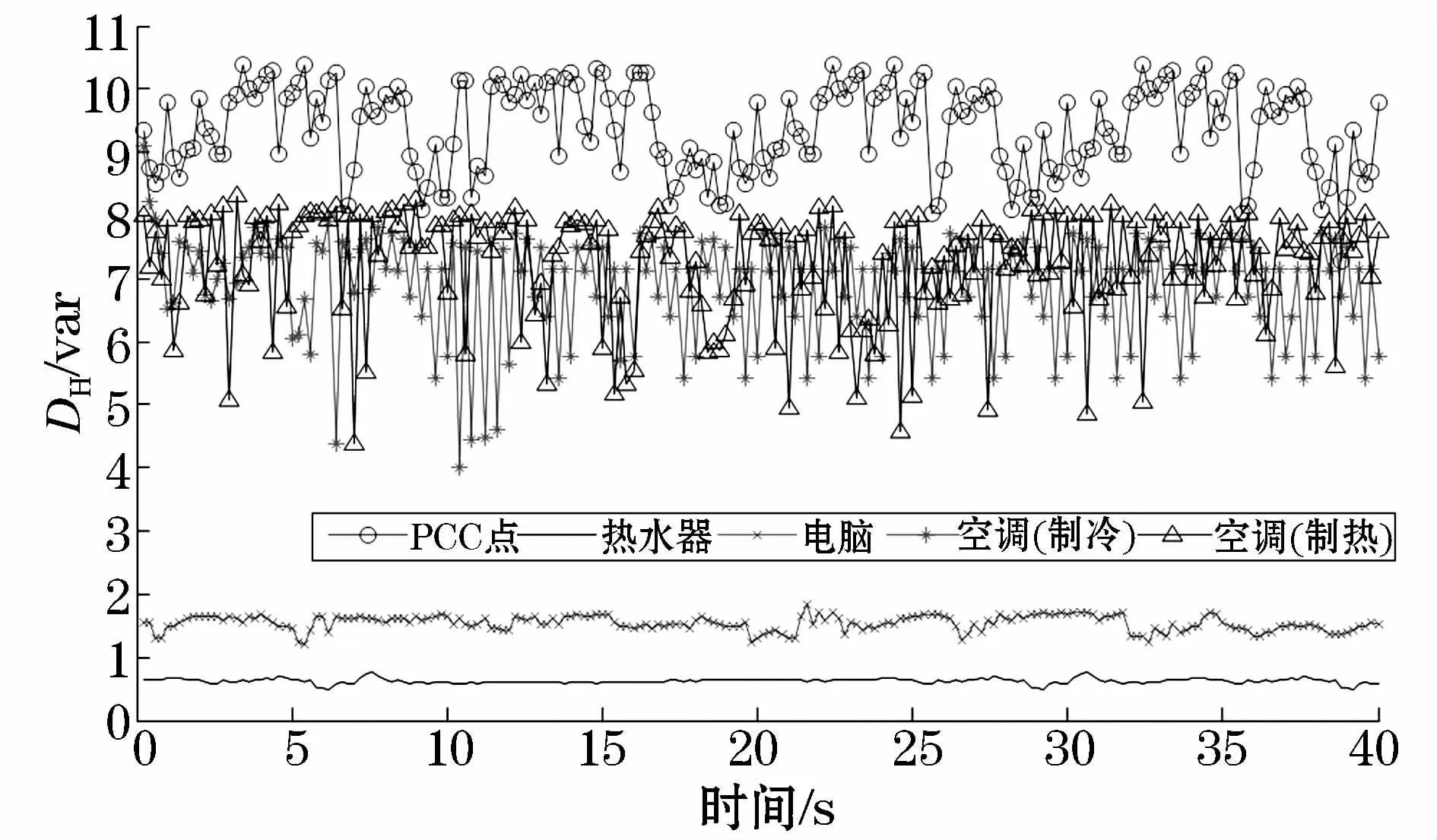
图8 负荷谐波畸变功率变化图Fig.8 Variation of loads in load harmonic distortion power

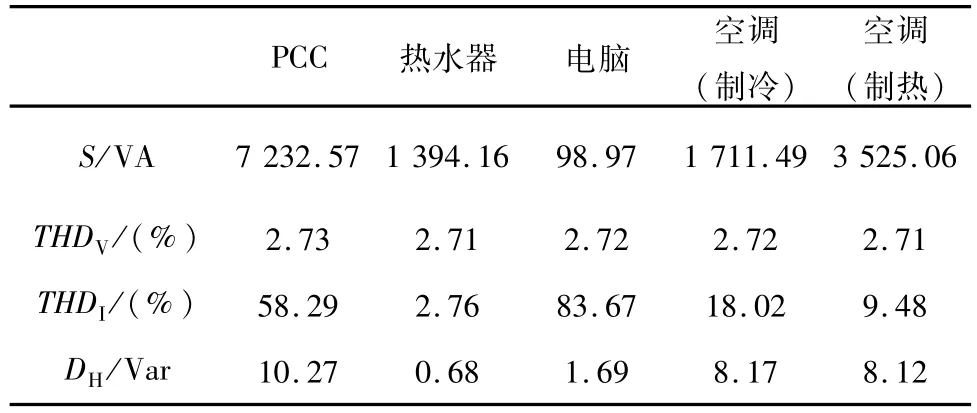
表4 实验数据结果Tab.4 Measurement results

5 结束语

提出了一种在供电网PCC点定位主谐波源的新方法，该方法基于标准IEEE Std.1459-2010的功率分解方法中定义的谐波畸变功率DH，通过仿真IEEE测试系统与现有的基于功率的方法进行了对比，结果表明该方法具有更高的准确度，实验部分对实际负荷的测量结果同样证明了此方法的正确性。此方法基于IEEE最新功率定义标准，更易于在工程中应用，如果与电网中大量采用的智能电表相结合，相信对电网的谐波治理具有重要作用，是未来值得重点研究的课题。