基于流体力学仿真的绝缘子空气动力结构多参数优化设计初探

刘世涛，何志强，王 博，，李秀广，张弓达，文习山

基于流体力学仿真的绝缘子空气动力结构多参数优化设计初探

刘世涛1，何志强2，王 博1，3，李秀广1，张弓达3，文习山3

（1.国网宁夏电力公司电力科学研究院，银川750002；2.宁夏送变电工程公司，银川 750001；3.武汉大学电气工程学院，武汉430072）

为了提高线路绝缘子在重风沙环境下的绝缘性能，最大限度发挥新型空气动力绝缘子的防污特性，基于绝缘子基本结构，提出了4个伞裙结构参数，并针对这些结构参数进行了基于流体场特性的优化设计仿真。4个伞裙结构参数作为优化设计输入参数，上层伞裙下方的矩形截面平均空气流速作为输出参数，分别以上层伞裙2个参数和下层伞裙2个参数各为1个影响因子组合，利用ANSYS Workbench平台进行流体力学计算和响应面优化设计。结合其他设计要求、经验和响应面优化结果，新型空气动力防污绝缘子外形结构的参数建议值可选取：上层伞裙半径L1为190 mm，上层伞裙小伞棱高度H1为8.7 mm，下层伞裙的半径L2为156 mm，下层伞裙在水平方向上的下倾角α为13°。

防污绝缘子；空气动力结构；计算流体力学；参数优化；响应面法

0 引言

输电线路设备运行环境恶劣，特别是线路绝缘子不仅是重要的机械结构设备，而且其绝缘性能直接影响线路安全运行。在重风沙环境中悬式绝缘子表面沙尘附着比较严重。线路绝缘子污秽闪络会对电力系统正常运行造成很大影响[1]。

绝缘子实体对空气流动有阻碍作用，伞裙附近会产生涡旋，空气流速低于外部环境流速。在沙尘区大风环境下，空气中裹挟的沙尘容易附着在绝缘子表面形成污秽层[2-5]。通过改变绝缘子外形结构，充分发挥伞裙的空气动力学特性，提高伞裙附近空气流速，减弱湍流作用，将有利于减少污秽沉积。

混合了沙尘的空气会伴随大气运动与绝缘子发生相互作用，沙尘颗粒有极大概率与绝缘子产生接触，并在一定条件下沉积于绝缘子表面形成积污[6-9]。多个研究指出，绝缘子附近沙尘颗粒所受到的空气曳力对它的运动过程产生决定性作用[10-14]。受空气曳力影响，污秽颗粒易于沉积在具有湍流的部位[15-18]。

绝缘子表面并非理想光滑平面，流动空气与绝缘子表面发生接触时，靠近固体表面的空气因粘滞作用而会降低流速，当外部气流速度较高时容易发展湍流，且绝缘子外形也很大程度上影响着附近流场的湍流特性。在不易形成湍流的平面附近，污秽颗粒运动速度高，即使与绝缘子发生接触也因自身动量较大而不易发生附着。在绝缘子附近形成湍流与气流速度降低的部位，是有利于污秽微粒沉积的区域[19-20]。若对物体形状进行流线型处理，缩减阻碍物横向尺度，则压差阻力明显下降，湍流强度和湍流区域也将明显减少[21]。

目前存在的空气动力型绝缘子，如双伞型或大伞径单伞型，其主要目的也是利用气流作用减少污秽物在绝缘子上、下表面的附着[5-6]。本文在现有空气动力型绝缘子外形结构的基础上做出一些探索，例如采用不等径双伞裙，增加上层伞裙小伞棱，以改善污秽物桥接问题。而空气动力特性与绝缘子结构密切相关，不同的结构参数会使绝缘子附近空气流场产生明显变化。

因此，笔者在提出的新型绝缘子基本结构基础模型上，设置4个结构参数，并考察参数变化时上层伞裙下部截平面的平均流速。绝缘子附近空气流场由计算流体力学软件仿真计算得出，并通过软件优化设计功能，得到最有利于提高伞裙附近空气流速的结构参数数值和参数组合，以保证提出的空气动力型防污结构具有优异性能。

1 新型空气动力型伞裙结构和尺寸参数

根据污秽颗粒在绝缘子附近空气流场中运动、沉积特点，以及气流与绝缘子作用时的绕流特性，应尽量使伞裙具有流线型结构，缩小横向气流阻碍物尺寸，以提高伞裙伞棱附近空气流速，减小湍流涡旋区，防止空气污秽物沉积在绝缘子表面。同时，应保持合适爬电距离，降低污秽闪络概率，也要兼顾生产制造、设计运行的特点，使绝缘子具有较好的实用价值。

笔者提出一种空气动力防污型悬挂式绝缘子基本结构，并设置4个结构尺寸参数作为优化设计对象，如图1所示。其中，钢帽和钢脚的结构尺寸与普通钟罩式绝缘子相同，瓷质或玻璃伞裙采用上、下双层不等径结构。上层伞裙倾斜角度与现有相同机械载荷等级的钟罩型绝缘子相同。上层伞裙最外侧具有一圈小伞棱，其他部位没有伞棱。瓷质或玻璃下层伞裙与水平方向呈一定下倾角度。

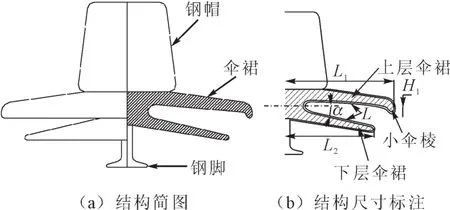
图1 空气动力防污型悬挂式绝缘子结构图Fig.1 The structure sketch of insulator with aerodynamic profile

设置的4个结构尺寸参数分别为上层伞裙的半径L1，上层伞裙小伞棱高度H1，下层伞裙的半径L2，下层伞裙在水平方向上的下倾角α。其中参数L1和H1共同决定了上层伞裙的外形，参数L2和α共同决定了下层伞裙的外形。一般情况下L1大于L2，非等径结构和使用边缘小伞棱充当落水缘将有利于增大伞间垂直距离，突出对雨水、冰凌和鸟粪等垂直形态绝缘破坏物的防护性能。下层伞裙保持一定倾斜角度α有利于遮蔽下层伞裙下表面区域，防止雨水浸湿下表面污层，并且有助于适当增加绝缘子整体爬电距离L。

当其中某一个结构参数发生变化时，绝缘子附近空气流场均不同，而将上层伞裙半径L1和小伞棱高度H1设置为一个参数变化组，以H1与L1的比值A作为一个衍生参数，来反映上层伞裙外形与空气流场的变化关系。同样的，设置下层伞裙半径L2和下倾角α为一个参数变化组，以α与L2的比值B作为另一个衍生参数，来反映下层伞裙外形与空气流场的变化关系，参数间关系为。

2 结构参数仿真优化

为了考察新型空气动力防污绝缘子4个结构参数对绝缘子附近流场的影响作用，笔者利用数值计算软件ANSYS Worksbench平台中的计算流体力学组件Fluent和优化设计模块，联合进行空气流场仿真和结构参数优化。

整个优化设计流程可分为5个部分：绝缘子模型导入，几何模型剖分，空气流体场数值计算，流体场结果提取和参数优化控制，流程图见图2。4个绝缘子结构参数作为输入参数，提取流体场特征参数作为输出参数，分别以上伞裙结构和下伞裙结构为优化对象建立两个设计项目。

图2 优化设计流程图Fig.2 The flow chart of optimization design

为了充分考虑成串绝缘子上下片之间影响，仿真模型使用3片绝缘子组成悬垂短串。绝缘子串和周围流体场具有对称性，为了节约计算资源，几何体和计算域均以绝缘子轴向截面为对称面建立1/2计算模型，计算域6.5 m×2 m×4 m。计算域速度入口的风速为8 m/s，用来模拟水平方向5级风；出口施加零压力扩散约束条件。绝缘子钢脚、钢帽和伞裙表面使用壁函数，计算域剩余面使用滑移条件。

各输入参数需要设定初始值和变化范围。参照U550BP/240H型钟罩绝缘子外形尺寸，上层伞裙的半径L1初始值定为190 mm，小伞棱高度H1初始值定为8.7 mm。考虑到上、下层伞裙间要保持适当的净空距离，而且也要照顾到组装钢帽、钢脚时需要预留出的操作空间，下层伞裙下倾角α初始值定为13°。结合整片绝缘子爬电距离要求和大小伞具有盘径差的约束，下层伞裙半径L2初始值定为156 mm。4个输入参数的数值均在初始值±10%范围内变化。输入参数初始值和变化范围见表1

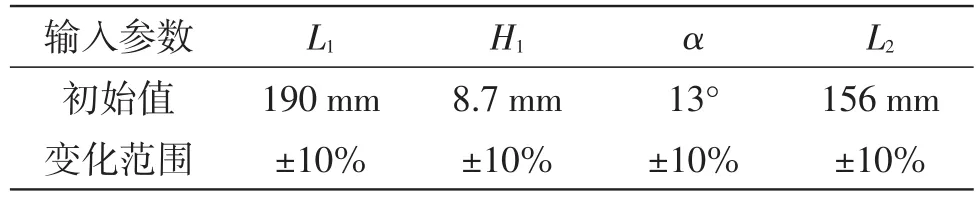
表1 输入参数初始值和变化范围Table 1 The initial value and variation range of input parameters

为了表明积污较严重的上下层伞裙间空气流场的流速特征，笔者在上下层伞裙间设置了一个矩形截面作为流速观察面（见图3），使用该平面的面平均流速Vave作为输出参数。Vave数值越大，表明该结构参数下的绝缘子具有更好的空气动力特性。

图3 流速观察面Fig.3 Observation plane of fluid velocity

笔者涉及的优化过程使用了实验设计（DOE）理论，主要目的是对输入参数备选值进行合理安排，以较小的仿真计算次数，获得理想的输入-输出响应结果。以响应面法作为实验设计优化方法，其基本原理是基于多个输入参数计算出目标解，从而建立一个响应面，在响应面极值处获得输入参数的最优组合[22-23]。多个输入参数的一个组合称为试验点，软件中使用常见的中心复合设计法规划试验点，并针对这些试验点进行求解。一旦求解完成，就能拟合出基于目标结果的响应面。比起离散的参数集赋值方法，响应面对应输入参数给出了连续变化的输出值[24]。

3 伞裙结构参数优化结果分析

在上层伞裙优化项目中，上层伞裙半径L1和小伞棱高度H1作为输入参数变化组合，当一个参数固定时，另一个参数与输出参数Vave之间具有二维曲线变化关系；两个参数组合与输出参数Vave之间具有三维曲面变化关系。当L1固定为初始值190 mm时，H1与Vave之间的变化关系见图4；当H1固定为初始值8.7 mm时，L1与Vave之间的变化关系见图5。L1、H1与Vave之间的响应面变化关系见图6。从图4至图6中可以看出，两输入参数L1和H1在定义域内变化时，输出参数Vave没有出现极值，也就是说上层伞裙伞径和小伞棱高度越小，对提高上下层伞裙间的空气流速越有利，而且伞径尺寸对伞裙间空气流速的影响更大。从实用性角度考虑，伞径伞棱设计尺寸不可能很小，这需要根据其他设计制造要求和经验给出合理数值。

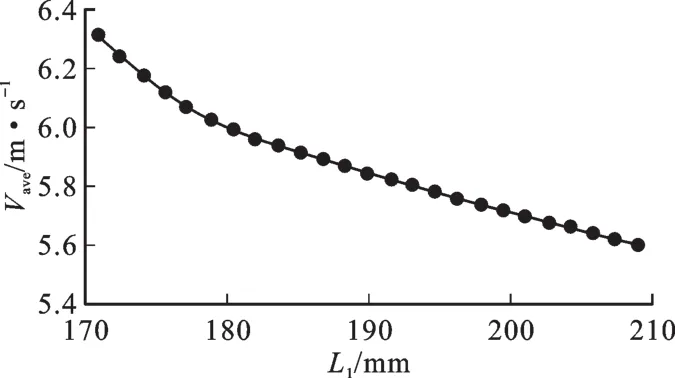
图4 输入参数L1与输出参数Vave二维变化关系Fig.4 Two-dimensional variable relation of L1and Vave

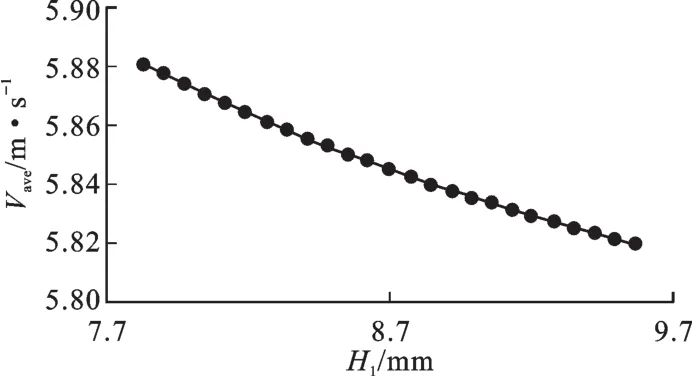
图5 输入参数H1与输出参数Vave二维变化关系Fig.5 Two-dimensional variable relation of H1and Vave

图6 输入参数L1、H1与输出参数Vave的响应面Fig.6 Response surface between L1，H1and Vave

在下层伞裙优化项目中，下层伞裙半径L2和伞裙下倾角α作为输入参数变化组合，当L2固定为初始值156 mm时，α与Vave之间的变化关系见图7；当α固定为初始值13°时，L2与Vave之间的变化关系见图8。L2、α与Vave之间的响应面变化关系见图9。图7、图8所示的两条曲线在参数变化范围内均具有极大值点。且在图9响应面图中也存在三维曲面极大值点，说明极大值对应的输入参数在一定取值范围内存在最优组合，即响应面上极大值所对应的两个输入参数伞裙下倾角α为13°和下层伞裙半径L2为156 mm时的参数组合为最优组合，此时反映下层伞裙外形与空气流场变化关系的衍生参数B的值约为0.083°/mm，上下层伞裙间的空气平均流速达到较高水平。

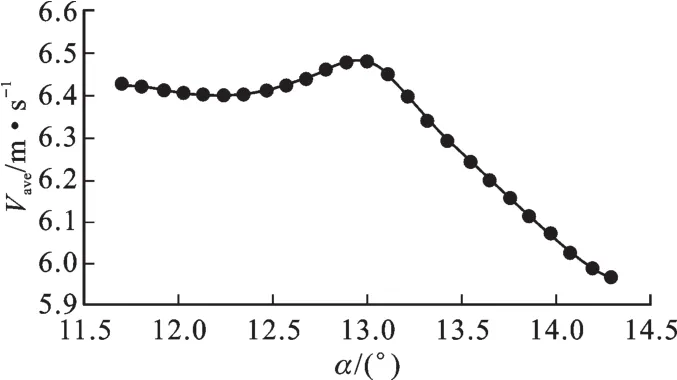
图7 输入参数α与输出参数Vave二维变化关系Fig.7 Two-dimensional variable relation of α and Vave

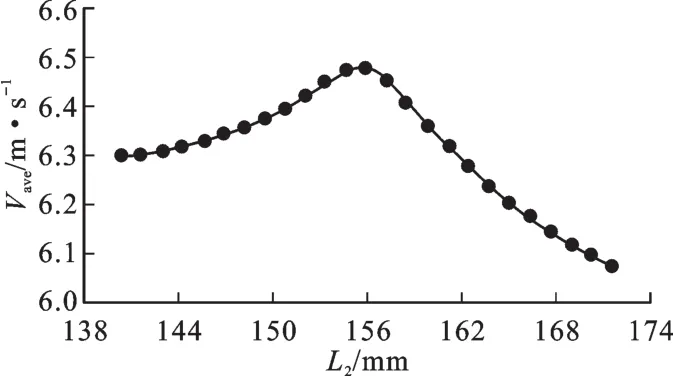
图8 输入参数L2与输出参数Vave二维变化关系Fig.8 Two-dimensional variable relation of L2and Vave

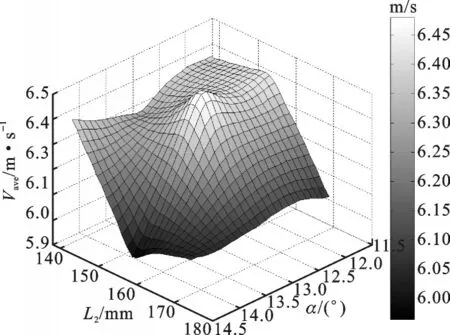
图9 输入参数α、L2与输出参数Vave的响应面Fig.9 Response surface between α、L2and Vave

考虑到表征上层伞裙外形的结构参数组合上层伞裙半径L1和小伞棱高度H1在响应面上不存在极值点，为了保证足够的爬电距离上层伞径不宜过小，并参考现有U550BP/240H型钟罩绝缘子伞裙半径，将L1定为190 mm。同时要考虑绝缘子生产制造难度，小伞棱高度H1也不宜过小，数值可暂定为8.7 mm。因此，反映上层伞裙外形与空气流场变化关系的衍生参数A的值约为0.046。而结合下层伞裙结构优化数据，表征新型空气动力防污绝缘子外形结构的参数优化结果可定为上层伞裙半径L1为190 mm，上层伞裙小伞棱高度H1为8.7 mm，下层伞裙的半径L2为156 mm，下层伞裙在水平方向上的下倾角α为13°。

4 结论

1）空气动力型防污绝缘子设计中，上层伞裙半径L1和上层伞裙小伞棱高度H1共同决定了上层伞裙基本结构；下层伞裙半径L2和下层伞裙下倾角α共同决定了下层伞裙基本结构。

2）上层伞裙的两个结构参数L1、H1与伞裙间截面平均流速Vave的响应曲面不存在极值点；考虑绝缘要求和制造工艺，并参照经验值，上层伞裙半径L1的值定为190 mm，上层伞裙小伞棱高度H1的值定为8.7 mm，衍生参数A的值约为0.046。

3）下层伞裙的两个结构参数L2、α与伞裙间截面平均流速Vave的响应曲面存在一个极大值点，所对应的两个结构参数数值作为最优组合，分别为下层伞裙半径L2为156 mm，下层伞裙α为13°，衍生参数B的值约为0.083°/mm。

4）经过结构参数优化后的防污绝缘子，具有更好的空气动力特性，其伞裙附近具有更高的空气流速。

[1]宿志一，李庆峰.我国电网防污闪措施的回顾和总结[J].电网技术，2010（12）:124-130.SU Zhiyi，LI Qingfeng.Historical review and summary on measures against pollution flashover occurred in power grids in China[J].Power System Technology，2010（12）：124-130.

[2]由长福，祁海鹰，徐旭常.湍流对气固两相流动中颗粒受力的影响[J].清华大学学报：自然科学版，2002，42（10）：1357-1360.YOU Changfu，QI Haiying，XU Xuchang.Effect of turbu⁃lence on the drag in a gas-particle two-phase flow[J].Jour⁃nal of Tsinghua University（Science and Technology），2002，42（10）:1357-1360.

[3]DUWAIRI H M，DAMSEH R A.Effect of thermophoresis particle deposition on mixed convection from vertical sur⁃faces embedded in saturated porous medium[J].Interna⁃tional Journal of Numerical Methods for Heat&Fluid Flow，2008，18（2）:202-216.

[4]刘洪涛.气固两相流中微细颗粒沉积与扩散特性的数值研究[D].重庆：重庆大学，2010.

[5]沈其荣，顾洪连.空气动力型直流玻璃绝缘子的生产和挂网运行[J].电瓷避雷器，2012（3）：6-8.SHEN Qirong，GU Honglian.Manufacture and service on the line of open profile type DC glass insulators[J].Insula⁃tors and Surge Arresters，2012（3）:6-8.

[6]张志劲，郑强，蒋兴良，等.空气动力型绝缘子表面不同区域的水滴撞击特性[J].高电压技术，2016（3）：900-907.ZHANG Zhijin，ZHENG Qiang，JIANG Xingliang，et al.Water droplet impingement characteristics on different re⁃gions ofaerodynamic insulator surface[J].High Voltage En⁃gineering，2016（3）：900-907.

[7]张志劲，李星，舒生前，等.XWP2-70双伞型绝缘子表面污秽颗粒积聚特性[J].高电压技术，2014，40（11）：3327-3335.ZHANG Zhijin，LI Xing，SHU Shengqian，et al.Charac⁃teristics of natural pollution accumulation of XWP2-70 in⁃sulators with double sheds[J].High Voltage Engineering，2014，40（11）:3327-3335.

[8]孙继星，徐跃，胡学永，等.高速气流环境中电气化铁路绝缘子表面积污分布特性[J].高电压技术，2014，40（1）：95-102.SUN Jixing，XU Yue，HU Xueyong，et al.Characteristics of pollution distribution on insulators nearby electrified railroad in high-speed aerosol[J].High Voltage Engineer⁃ing，2014，40（1）:95-102.

[9]叶晓君，何维，李恒真，等.低风速条件下污秽颗粒在电力外绝缘近表面的动力模型研究[J].电瓷避雷器，2012（6）：19-25.YE Xiaojun，HE Wei，LI Hengzhen，et al.Study on a dy⁃namic model of pollution particles on the near surface of electric external insulation under low wind speed condition[J].Insulators and Surge Arresters，2012，06（6）:19-25.

[10]袁竹林，朱立平.气固两相流动与数值模拟[M].南京：东南大学出版社，2013.

[11]施学贵，徐旭常，冯俊凯.颗粒在湍流气流中运动的受力分析[J].工程热物理学报，1989（10）：320-325.SHI Xuegui，XU Xuchang，FENG Junkai.The analysis of forces on particles moving in turbulent flow[J].Journal of Engineering Thermo Physics，1989（10）：320-325.

[12]董长银，栾万里，周生田，等.牛顿流体中的固体颗粒运动模型分析及应用[J].中国石油大学学报:自然科学版，2007，31（5）：55-59.DONG Changyin，LUAN Wanli，ZHOU Shengtian，et al.Analysis and application of model for solid particle move⁃ment in Newton fluid[J].Journal of China University of Pe⁃troleum（Edition of Natural Science），2007，31（5）:55-59.

[13]丛晓春，张旭.开放性尘源粉尘运动轨迹的数值计算[J].同济大学学报:自然科学版，2005，33（3）：330-333.CONG Xiaochun，ZHANG Xu.Numerical calculation of open-air source powder velocity trail[J].Journal of Tongji University（Natural Science），2005，33（3）:330-333.

[14]岑可法，樊建人.煤粉颗粒在气流中的受力分析及其运动轨迹的研究[J].浙江大学学报，1987（21）:1-11.CEN Kefa，FAN Jianren.The analysis of the forces acting on coal particles and the trajectories in the gas flows[J].Journal of Zhejiang University：Natural Science，1987（21）：1-11.

[15]陈香.风场湍流特性对散状颗粒物风蚀污染的影响研究[D].青岛：山东科技大学，2011.

[16]刘洪涛，张力，陈艳容.气固两相圆柱绕流背风区颗粒的运动特性[J].重庆大学学报，2010，33（4）：54-59.LIU Hongtao，ZHANG Li，CHEN Yanrong.Investigations of the particle motion characteristics in the gas-solid twophase wake of leeward side circular cylinder[J].Journal of Chongqing University（Natural Science Edition），2010，33（4）:54-59.

[17]张利珍，李运泽，王浚.气固两相流风洞内颗粒运动特性研究[J].系统仿真学报，2007，19（14）：3200-3202.ZHANG Lizhen，LI Yunze，WANG Jun.Study on particle flow character in gas/solid two-phase wind tunnel[J].Jour⁃nal of System Simulation，2007，19（14）:3200-3202.

[18]韩云龙，殷传慧，胡永梅.通风管道结构形式对颗粒物沉积的影响[J].过程工程学报，2015，15（1）：40-44.HAN Yunlong，YAN Chuanhui，HU Yongmei.Effect of ventilation duct structure on deposition of particles[J].The Chinese Journal of Process Engineering，2015，15（1）:40-44.

[19]孙继星，吴广宁，陈维荣，等.强风环境下棒形绝缘子积污动态仿真分析[J].西南交通大学学报，2012，47（3）：413-419.SUN Jixing，WU Guangning，CHEN Weirong，et al.Dy⁃namic simulation analysis of bar insulator pollution in strong wind[J].Journal of Southwest Jiaotong University，2012，47（3）:413-419.

[20]李海波.基于流体力学原理的悬垂绝缘子串积污特性研究[D].重庆：重庆大学，2010.

[21]李万平.计算流体力学[M].武汉：华中科技大学出版社，2004.

[22]蒙哥马利.实验设计与分析[M].北京：人民邮电出版社，2009.

[23]刘文卿.实验设计[M].北京：清华大学出版社，2005.

[24]王国峰.Workbench的基础应用:流体仿真[M].北京：国防工业出版社，2012.

Preliminary Discussion on Multi Parameter Optimization Design of Insulator Aerodynamic Structure Based on Fluid Dynamics Simulation

LIU Shitao1，HE Zhiqiang2，WANG Bo1，3，LI Xiuguang1，ZHANG Gongda3，WEN Xishan3
（1.Electric Power Research Institute，State Grid Ningxia Electrical Power Company，Yinchuan 750002，China；2.Ningxia Electric Power Transmission and Transformation Engineering Company，Yinchuan 750001，Chian;3.School of Electrical Engineering，Wuhan University，Wuhan 430072，China）

In this paper，four structure parameters of sheds are defined based on the sample of aero dynamical antifouling insulator，and the fluid field simulations for the parameters optimization are done in order to improve the insulator performance under the environment of windy and dusty，maximize the anti⁃fouling characteristic of new aerodynamic insulator.The four structure parameters of sheds are set to the input parameters，and the area-weighted average air velocity on the rectangle cut plane under the upper shed is set to the output parameter in the optimization work.The two structure parameters related to upper shed or lower shed are set to one factors group to establish a design project.The fluid dynamics simula⁃tion and optimization design with response surface method are operated on the software platform of AN⁃SYS workbench.According to the response surface optimization results and other design experiences，the values of structure parameters of new aero dynamical may be suggested as:the radius of upper shedL1is 190mm，the height of small rib at the edge of upper shedH1is 8.7mm，the radius of lower shedL2is 156mm，the downward inclination angle of lower shed α is 13°.

antifouling insulator；aerodynamic structure；computational fluid dynamics；parameter optimization；response surface method

10.16188/j.isa.1003-8337.2017.06.042

2017-04-28

刘世涛（1986—），工程师，现从事输电线路技术监督和电网防污闪工作。